华师大版数学八年级上16.3梯形导学案(共2课时)
文档属性
| 名称 | 华师大版数学八年级上16.3梯形导学案(共2课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 58.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-22 00:00:00 | ||
图片预览

文档简介
初二数学《平行四边形的认识》第三节梯形的性质(第 1 课时)导学案(P109-110)
学习目标: 1、掌握等腰梯形的判定定理,并能应用它进行有关证明;
2 、通过添加辅助线,把梯形问题转化为平行四边形或三角形问题,体会图形变换的方法和转化思想。
学 习 过 程 一、知识衔接回顾 基础定义自学
1.前面已经研究了两组对边分别平行的四边形( ),现在我们研究只有一组对边平行的另一种特殊四边形.(1)梯形的定义:一组对边 而另一组对边 的四边形叫做梯形.注意:定义需满足三个条件:①四边形;②一组对边 ;③一组对边 .
(2)梯形的相关定义:①梯形的底:梯形中 的两边叫做梯形的底.
注意:通常把较短的底叫做 ,较长的底叫做 ,梯形的上下底则是以长短区分的,不是指位置定的.
②梯形的腰:梯形中不平行的两边叫做梯形的 .
③梯形的高:梯形两底的 叫做梯形的高.
(3)特殊梯形的定义: ①等腰梯形: 的梯形叫做等腰梯形.
②直角梯形:一腰 的梯形叫做直角梯形.
2.梯形的分类:(如图所示) 标出下列图形的名称
( ) ( ) ( )
议一议
(1)如图,四边形ABCD中,当 ,
且AB不平行于CD时,四边形ABCD
是梯形。
(2)如图,梯形ABCD中,AD∥BC,
则上底是 ,下底是 ,腰 第 1、2、3题图
是 。
(3)如图,梯形ABCD中,AD∥BC,当 = 时,梯形ABCD是等腰梯形。
二、新知自学
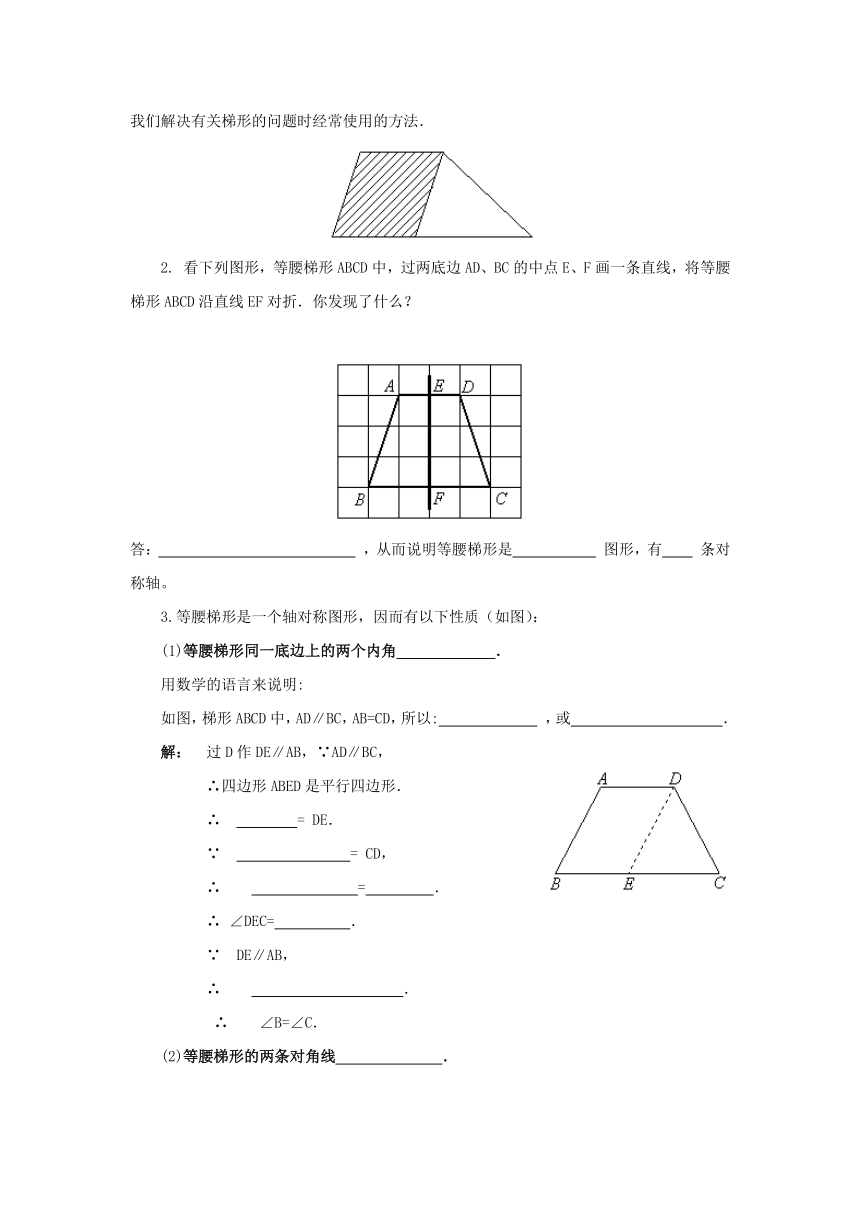
1.看下列图形,梯形总可以看成是一个 与一个 的组合,这也是我们解决有关梯形的问题时经常使用的方法.
2. 看下列图形,等腰梯形ABCD中,过两底边AD、BC的中点E、F画一条直线,将等腰梯形ABCD沿直线EF对折.你发现了什么?
答: ,从而说明等腰梯形是 图形,有 条对称轴。
3.等腰梯形是一个轴对称图形,因而有以下性质(如图):
(1)等腰梯形同一底边上的两个内角 .
用数学的语言来说明:
如图,梯形ABCD中,AD∥BC,AB=CD,所以: ,或 .
解: 过D作DE∥AB,∵AD∥BC,
∴四边形ABED是平行四边形.
∴ = DE.
∵ = CD,
∴ = .
∴ ∠DEC= .
∵ DE∥AB,
∴ .
∴ ∠B=∠C.
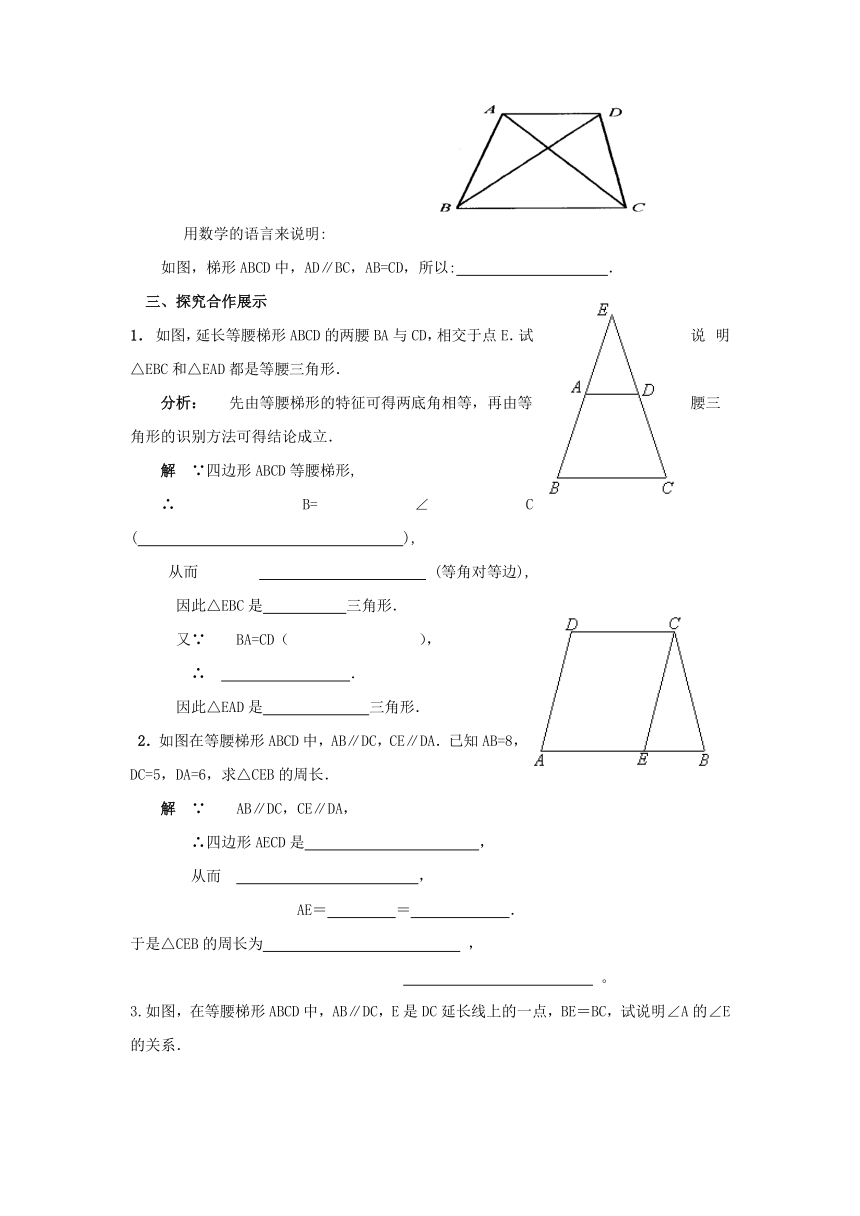
(2)等腰梯形的两条对角线 .
用数学的语言来说明:
如图,梯形ABCD中,AD∥BC,AB=CD,所以: .
三、探究合作展示
1. 如图,延长等腰梯形ABCD的两腰BA与CD,相交于点E.试说明△EBC和△EAD都是等腰三角形.
分析: 先由等腰梯形的特征可得两底角相等,再由等腰三角形的识别方法可得结论成立.
解 ∵四边形ABCD等腰梯形,
∴ B=∠C ( ),
从而 (等角对等边),
因此△EBC是 三角形.
又∵ BA=CD( ),
∴ .
因此△EAD是 三角形.
2.如图在等腰梯形ABCD中,AB∥DC,CE∥DA.已知AB=8,DC=5,DA=6,求△CEB的周长.
解 ∵ AB∥DC,CE∥DA,
∴四边形AECD是 ,
从而 ,
AE= = .
于是△CEB的周长为 ,
。
3.如图,在等腰梯形ABCD中,AB∥DC,E是DC延长线上的一点,BE=BC,试说明∠A的∠E的关系.
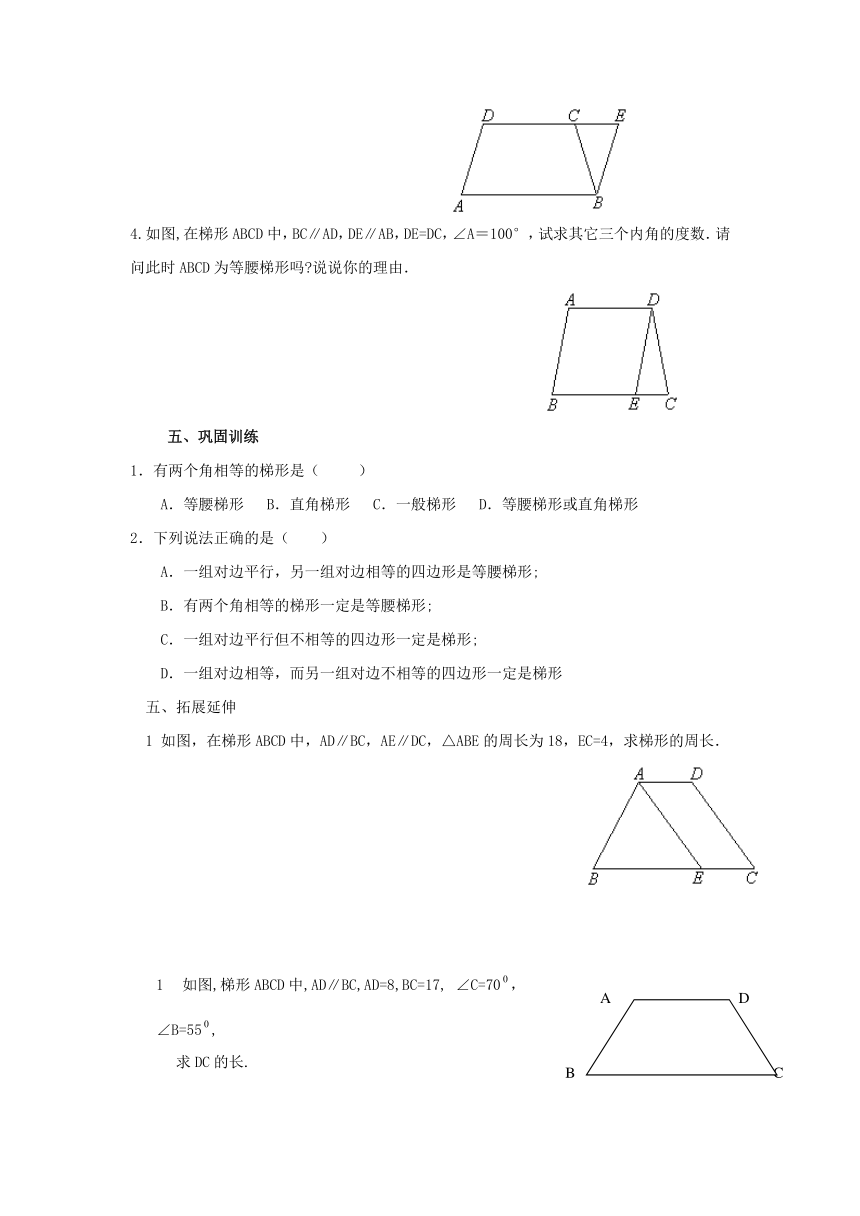
4.如图,在梯形ABCD中,BC∥AD,DE∥AB,DE=DC,∠A=100°,试求其它三个内角的度数.请问此时ABCD为等腰梯形吗 说说你的理由.
五、巩固训练
1.有两个角相等的梯形是( )
A.等腰梯形 B.直角梯形 C.一般梯形 D.等腰梯形或直角梯形
2.下列说法正确的是( )
A.一组对边平行,另一组对边相等的四边形是等腰梯形;
B.有两个角相等的梯形一定是等腰梯形;
C.一组对边平行但不相等的四边形一定是梯形;
D.一组对边相等,而另一组对边不相等的四边形一定是梯形
五、拓展延伸
1 如图,在梯形ABCD中,AD∥BC,AE∥DC,△ABE的周长为18,EC=4,求梯形的周长.
如图,梯形ABCD中,AD∥BC,AD=8,BC=17, ∠C=70,
∠B=55,
求DC的长.
3 如图,在等腰梯形ABCD中,AB=DC, ∠B=60°, DE∥AB.试说明
(1) DE=DC;
(2) △DEC是一个等边三角形.
初二数学《平行四边形的认识》第三节梯形的性质(第 2 课时)导学案(P110-111)
学习目标:
1.运用梯形、等腰梯形、直角梯形的有关知识进行计算、说理;
2.能恰当地添加辅助线把有关梯形的问题转化成平行四边形和三角形来解决.
3.通过添加辅助线,能用熟悉的平行四边形和三角形解决梯形问题,从而感受到数学学习中的化归思想.
教学过程:
一、知识衔接回顾
上节课我们学习了梯形、等腰梯形、直角梯形,下面我们先回忆一下什么是等腰梯形、直角梯形.
两 的梯形叫做等腰梯形,有一个角是 的梯形叫做直角梯形.(如图所示)
( ) ( )
等腰梯形的性质:
(1)等腰梯形的 相等. (2)等腰梯形是 图形.
(3)等腰梯形 的两个内角相等. (4)等腰梯形的两条对角线 .
二、新知自学
做一做
梯形中常用的添加辅助线的方法如下:..
( )( ) ( )( )
1.如图,在等腰梯形ABCD中,AD∥BC,AB=CD,∠C=60°,AD=15cm,BC=49cm,求CD的长
. 分析: 构造三角形和平行四边形来解,常用方法是过D作AB的平行线,把等腰梯形ABCD化为平行四边形ABED和等边三角形ECD.
解: 过D作DE∥AB交BC于E,
则四边形ABED为 .
∴ ,
2.如图,在梯形ABCD中,AB∥CD,对角线AC⊥BD,且AC=4,BD=5,求梯形的面积.
分析: 添加梯形对角线的平行线构造平行四边形BDCE和直角三角形ACE.
解: 过点C作CE∥BD交AB的延长线于点E,
又AB∥CD,
∴四边形BDCE为 .
因此CE= = ,BE= .
又∵C到BE的距离等于A到CD的距离
∴S△ACD=S△BEC.
从而S梯形ABCD=S△ .
∵AC⊥BD,CE∥BD,∴AC⊥ ,
.
三、探究合作展示
(一)归纳:添加辅助线可以把有关梯形的问题转化成平行四边形和三角形来解决.
1.解决梯形问题的基本思路:.
这种思路常通过平移或旋转来实现.
2.梯形的面积: .
(二).合作探究
1、过A、D两点作等腰梯形ABCD的高AE、DF,则分成三个什么样图形,有哪些相等的线段和角?
答:
2、若将等腰梯形的一条对角线平移至如图位置,还能得到哪些特殊图形?若将BD平移呢?
答:
3、在梯形ABCD中,AB∥CD,AD=BC,延长AB到E使BE=CD,求证:AC=CE
4、梯形ABCD中,AD//BC,AB=CD=4cm,AD=3cm,∠B=60 , 求 梯形ABCD的面积
四、巩固训练
1.下列说法正确的是( )
A.平行四边形是一种特殊的梯形;B.等腰梯形两底角相等
C.等腰梯形不可能是直角梯形; D.有两邻角相等的梯形是等腰梯形
2.梯形的上底长为6cm,过上底一个顶点引一腰的平行线,交下底所得的三角形的周长是19cm,那么这个梯形的周长是( ) A.31cm B.25cm C.19cm D.28cm
3.如果等腰梯形两底差的一半等于它的高,则这个梯形的一个底角等于( )
A.30° B.45° C.60° D.75°
4.在梯形ABCD中,AD∥BC,∠C=70°,则∠D= .
5.已知梯形上底长为2,下底长为5,一腰长为4,则另一腰x的取值范围是 .
6.等腰梯形的一个锐角等于60°,它的上底是3cm,腰长是4cm,则下底是____.
7.如图1,等腰梯形ABCD中,AD∥BC,AD=AB=BC.若梯形的周长是30cm,则AD=________cm,∠B=______.
(1) (2) (3) (4)
8.如图2,在梯形ABCD中,AD∥BC,CA平分∠BCD,CD=5,则AD的长是
9.如图3所示,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB的度数为_______.
10.如图4,是用形状、大小完全相同的等腰梯形密铺成的图案,则这个图案中的等腰梯形的底角(指锐角)是______度.
11、如图,在梯形ABCD中,AD∥BC,E是CD的中点,EF⊥AB,于点F,AB=6㎝,EF=5㎝,求梯形ABCD的面积。
五、拓展延伸
1.梯形ABCD中,AB∥CD,∠A=60°,∠B=60°,CD=3cm,AD=10cm,则AB的长是________cm.
2.直角梯形的一腰与底边夹角为60°,此腰与上底的长都是8cm,则梯形的周长是________.
3.如图,等腰梯形ABCD中,AD∥BC,AC⊥BD,AD+BC=26,求梯形ABCD的高.
C
B
D
C
B
A
A
C
B
·
D
F
E
学习目标: 1、掌握等腰梯形的判定定理,并能应用它进行有关证明;
2 、通过添加辅助线,把梯形问题转化为平行四边形或三角形问题,体会图形变换的方法和转化思想。
学 习 过 程 一、知识衔接回顾 基础定义自学
1.前面已经研究了两组对边分别平行的四边形( ),现在我们研究只有一组对边平行的另一种特殊四边形.(1)梯形的定义:一组对边 而另一组对边 的四边形叫做梯形.注意:定义需满足三个条件:①四边形;②一组对边 ;③一组对边 .
(2)梯形的相关定义:①梯形的底:梯形中 的两边叫做梯形的底.
注意:通常把较短的底叫做 ,较长的底叫做 ,梯形的上下底则是以长短区分的,不是指位置定的.
②梯形的腰:梯形中不平行的两边叫做梯形的 .
③梯形的高:梯形两底的 叫做梯形的高.
(3)特殊梯形的定义: ①等腰梯形: 的梯形叫做等腰梯形.
②直角梯形:一腰 的梯形叫做直角梯形.
2.梯形的分类:(如图所示) 标出下列图形的名称
( ) ( ) ( )
议一议
(1)如图,四边形ABCD中,当 ,
且AB不平行于CD时,四边形ABCD
是梯形。
(2)如图,梯形ABCD中,AD∥BC,
则上底是 ,下底是 ,腰 第 1、2、3题图
是 。
(3)如图,梯形ABCD中,AD∥BC,当 = 时,梯形ABCD是等腰梯形。
二、新知自学
1.看下列图形,梯形总可以看成是一个 与一个 的组合,这也是我们解决有关梯形的问题时经常使用的方法.
2. 看下列图形,等腰梯形ABCD中,过两底边AD、BC的中点E、F画一条直线,将等腰梯形ABCD沿直线EF对折.你发现了什么?
答: ,从而说明等腰梯形是 图形,有 条对称轴。
3.等腰梯形是一个轴对称图形,因而有以下性质(如图):
(1)等腰梯形同一底边上的两个内角 .
用数学的语言来说明:
如图,梯形ABCD中,AD∥BC,AB=CD,所以: ,或 .
解: 过D作DE∥AB,∵AD∥BC,
∴四边形ABED是平行四边形.
∴ = DE.
∵ = CD,
∴ = .
∴ ∠DEC= .
∵ DE∥AB,
∴ .
∴ ∠B=∠C.
(2)等腰梯形的两条对角线 .
用数学的语言来说明:
如图,梯形ABCD中,AD∥BC,AB=CD,所以: .
三、探究合作展示
1. 如图,延长等腰梯形ABCD的两腰BA与CD,相交于点E.试说明△EBC和△EAD都是等腰三角形.
分析: 先由等腰梯形的特征可得两底角相等,再由等腰三角形的识别方法可得结论成立.
解 ∵四边形ABCD等腰梯形,
∴ B=∠C ( ),
从而 (等角对等边),
因此△EBC是 三角形.
又∵ BA=CD( ),
∴ .
因此△EAD是 三角形.
2.如图在等腰梯形ABCD中,AB∥DC,CE∥DA.已知AB=8,DC=5,DA=6,求△CEB的周长.
解 ∵ AB∥DC,CE∥DA,
∴四边形AECD是 ,
从而 ,
AE= = .
于是△CEB的周长为 ,
。
3.如图,在等腰梯形ABCD中,AB∥DC,E是DC延长线上的一点,BE=BC,试说明∠A的∠E的关系.
4.如图,在梯形ABCD中,BC∥AD,DE∥AB,DE=DC,∠A=100°,试求其它三个内角的度数.请问此时ABCD为等腰梯形吗 说说你的理由.
五、巩固训练
1.有两个角相等的梯形是( )
A.等腰梯形 B.直角梯形 C.一般梯形 D.等腰梯形或直角梯形
2.下列说法正确的是( )
A.一组对边平行,另一组对边相等的四边形是等腰梯形;
B.有两个角相等的梯形一定是等腰梯形;
C.一组对边平行但不相等的四边形一定是梯形;
D.一组对边相等,而另一组对边不相等的四边形一定是梯形
五、拓展延伸
1 如图,在梯形ABCD中,AD∥BC,AE∥DC,△ABE的周长为18,EC=4,求梯形的周长.
如图,梯形ABCD中,AD∥BC,AD=8,BC=17, ∠C=70,
∠B=55,
求DC的长.
3 如图,在等腰梯形ABCD中,AB=DC, ∠B=60°, DE∥AB.试说明
(1) DE=DC;
(2) △DEC是一个等边三角形.
初二数学《平行四边形的认识》第三节梯形的性质(第 2 课时)导学案(P110-111)
学习目标:
1.运用梯形、等腰梯形、直角梯形的有关知识进行计算、说理;
2.能恰当地添加辅助线把有关梯形的问题转化成平行四边形和三角形来解决.
3.通过添加辅助线,能用熟悉的平行四边形和三角形解决梯形问题,从而感受到数学学习中的化归思想.
教学过程:
一、知识衔接回顾
上节课我们学习了梯形、等腰梯形、直角梯形,下面我们先回忆一下什么是等腰梯形、直角梯形.
两 的梯形叫做等腰梯形,有一个角是 的梯形叫做直角梯形.(如图所示)
( ) ( )
等腰梯形的性质:
(1)等腰梯形的 相等. (2)等腰梯形是 图形.
(3)等腰梯形 的两个内角相等. (4)等腰梯形的两条对角线 .
二、新知自学
做一做
梯形中常用的添加辅助线的方法如下:..
( )( ) ( )( )
1.如图,在等腰梯形ABCD中,AD∥BC,AB=CD,∠C=60°,AD=15cm,BC=49cm,求CD的长
. 分析: 构造三角形和平行四边形来解,常用方法是过D作AB的平行线,把等腰梯形ABCD化为平行四边形ABED和等边三角形ECD.
解: 过D作DE∥AB交BC于E,
则四边形ABED为 .
∴ ,
2.如图,在梯形ABCD中,AB∥CD,对角线AC⊥BD,且AC=4,BD=5,求梯形的面积.
分析: 添加梯形对角线的平行线构造平行四边形BDCE和直角三角形ACE.
解: 过点C作CE∥BD交AB的延长线于点E,
又AB∥CD,
∴四边形BDCE为 .
因此CE= = ,BE= .
又∵C到BE的距离等于A到CD的距离
∴S△ACD=S△BEC.
从而S梯形ABCD=S△ .
∵AC⊥BD,CE∥BD,∴AC⊥ ,
.
三、探究合作展示
(一)归纳:添加辅助线可以把有关梯形的问题转化成平行四边形和三角形来解决.
1.解决梯形问题的基本思路:.
这种思路常通过平移或旋转来实现.
2.梯形的面积: .
(二).合作探究
1、过A、D两点作等腰梯形ABCD的高AE、DF,则分成三个什么样图形,有哪些相等的线段和角?
答:
2、若将等腰梯形的一条对角线平移至如图位置,还能得到哪些特殊图形?若将BD平移呢?
答:
3、在梯形ABCD中,AB∥CD,AD=BC,延长AB到E使BE=CD,求证:AC=CE
4、梯形ABCD中,AD//BC,AB=CD=4cm,AD=3cm,∠B=60 , 求 梯形ABCD的面积
四、巩固训练
1.下列说法正确的是( )
A.平行四边形是一种特殊的梯形;B.等腰梯形两底角相等
C.等腰梯形不可能是直角梯形; D.有两邻角相等的梯形是等腰梯形
2.梯形的上底长为6cm,过上底一个顶点引一腰的平行线,交下底所得的三角形的周长是19cm,那么这个梯形的周长是( ) A.31cm B.25cm C.19cm D.28cm
3.如果等腰梯形两底差的一半等于它的高,则这个梯形的一个底角等于( )
A.30° B.45° C.60° D.75°
4.在梯形ABCD中,AD∥BC,∠C=70°,则∠D= .
5.已知梯形上底长为2,下底长为5,一腰长为4,则另一腰x的取值范围是 .
6.等腰梯形的一个锐角等于60°,它的上底是3cm,腰长是4cm,则下底是____.
7.如图1,等腰梯形ABCD中,AD∥BC,AD=AB=BC.若梯形的周长是30cm,则AD=________cm,∠B=______.
(1) (2) (3) (4)
8.如图2,在梯形ABCD中,AD∥BC,CA平分∠BCD,CD=5,则AD的长是
9.如图3所示,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB的度数为_______.
10.如图4,是用形状、大小完全相同的等腰梯形密铺成的图案,则这个图案中的等腰梯形的底角(指锐角)是______度.
11、如图,在梯形ABCD中,AD∥BC,E是CD的中点,EF⊥AB,于点F,AB=6㎝,EF=5㎝,求梯形ABCD的面积。
五、拓展延伸
1.梯形ABCD中,AB∥CD,∠A=60°,∠B=60°,CD=3cm,AD=10cm,则AB的长是________cm.
2.直角梯形的一腰与底边夹角为60°,此腰与上底的长都是8cm,则梯形的周长是________.
3.如图,等腰梯形ABCD中,AD∥BC,AC⊥BD,AD+BC=26,求梯形ABCD的高.
C
B
D
C
B
A
A
C
B
·
D
F
E
