2020-2021学年苏科版数学七年级下册第七章《平面图形的认识(二)》易错题专练(三)(Word版 含解析)
文档属性
| 名称 | 2020-2021学年苏科版数学七年级下册第七章《平面图形的认识(二)》易错题专练(三)(Word版 含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 122.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-21 00:00:00 | ||
图片预览


文档简介
2020-2021学年七年级下册第七章《平面图形的认识(二)》
易错题专练(三)
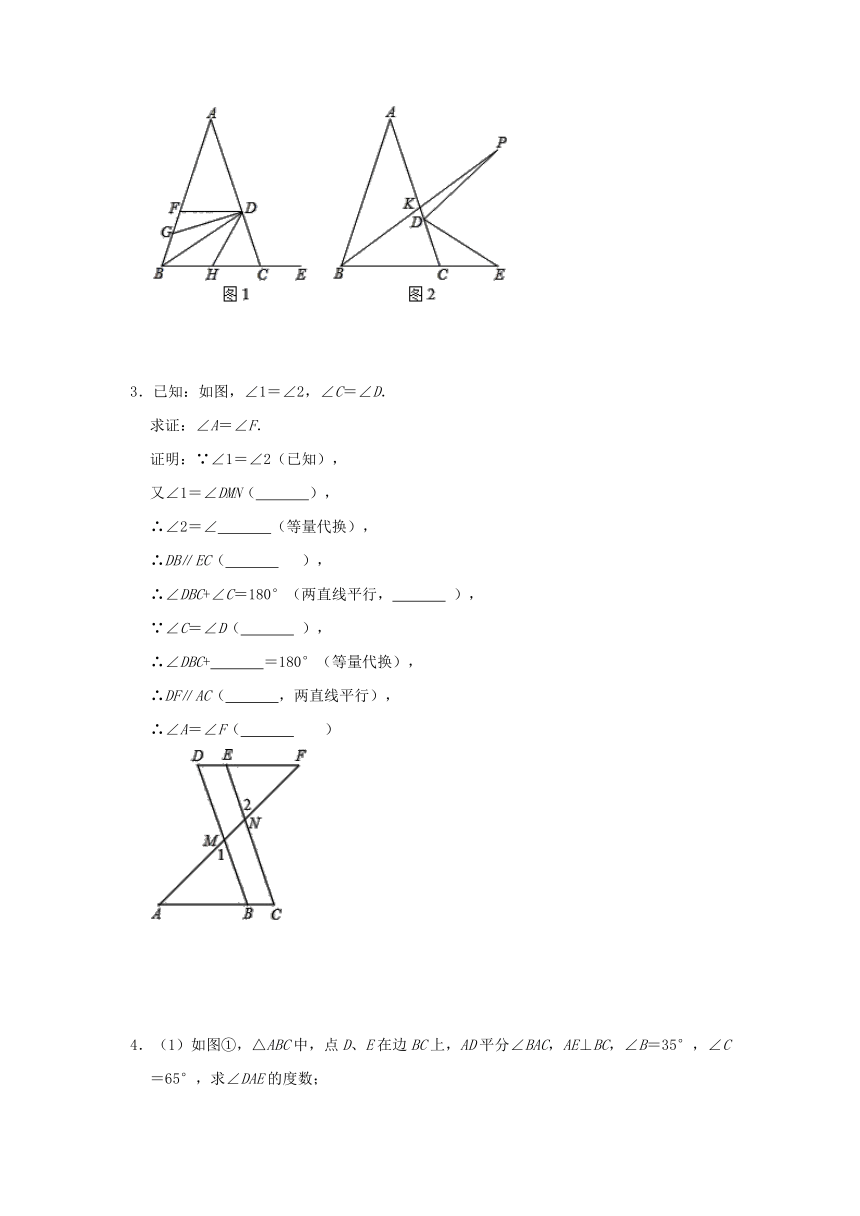
1.已知如图①,BP、CP分别是△ABC的外角∠CBD、∠BCE的角平分线,BQ、CQ分别是∠PBC、∠PCB的角平分线,BM、CN分别是∠PBD、∠PCE的角平分线,∠BAC=α.
(1)当α=40°时,∠BPC=
°,∠BQC=
°;
(2)当α=
°时,BM∥CN;
(3)如图②,当α=120°时,BM、CN所在直线交于点O,求∠BOC的度数;
(4)在α>60°的条件下,直接写出∠BPC、∠BQC、∠BOC三角之间的数量关系:
.
2.已知,如图,E为BC延长线上一点,点D是线段AC上一点.
(1)如图1,DF∥BC,作DG平分∠BDF交AB于G,DH平分∠GDC交BC于H,且∠BDC比∠ACB大20°,求∠GDH的度数.
(2)如图2,连接DE,若∠ABC的平分线与∠ADE的平分线相交于点P,BP交AC于点K.
①设∠ABK=x,∠AKB=y,∠ADP=z,试用x,y,z表示∠E;
②求证:∠P=(∠A﹣∠E).
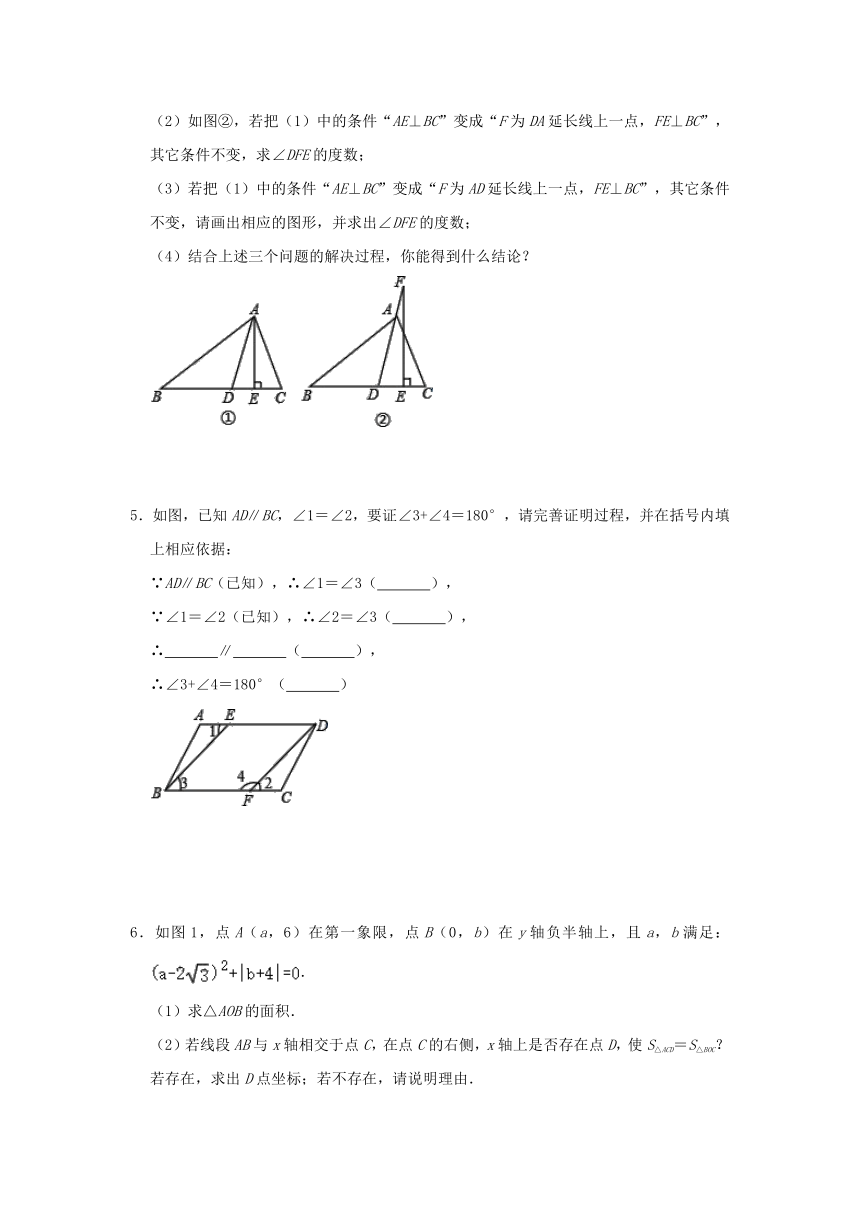
3.已知:如图,∠1=∠2,∠C=∠D.
求证:∠A=∠F.
证明:∵∠1=∠2(已知),
又∠1=∠DMN(
),
∴∠2=∠
(等量代换),
∴DB∥EC(
),
∴∠DBC+∠C=180°(两直线平行,
),
∵∠C=∠D(
),
∴∠DBC+
=180°(等量代换),
∴DF∥AC(
,两直线平行),
∴∠A=∠F(
)
4.(1)如图①,△ABC中,点D、E在边BC上,AD平分∠BAC,AE⊥BC,∠B=35°,∠C=65°,求∠DAE的度数;
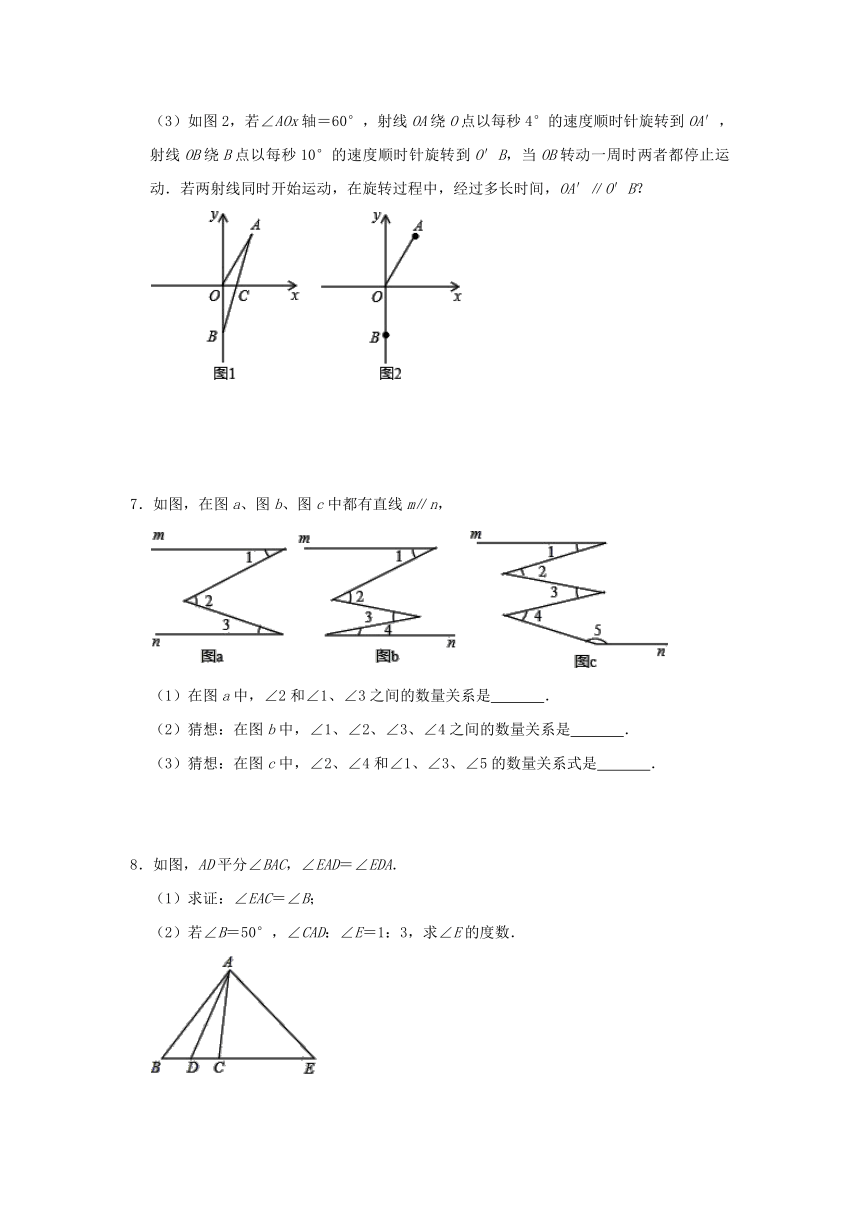
(2)如图②,若把(1)中的条件“AE⊥BC”变成“F为DA延长线上一点,FE⊥BC”,其它条件不变,求∠DFE的度数;
(3)若把(1)中的条件“AE⊥BC”变成“F为AD延长线上一点,FE⊥BC”,其它条件不变,请画出相应的图形,并求出∠DFE的度数;
(4)结合上述三个问题的解决过程,你能得到什么结论?
5.如图,已知AD∥BC,∠1=∠2,要证∠3+∠4=180°,请完善证明过程,并在括号内填上相应依据:
∵AD∥BC(已知),∴∠1=∠3(
),
∵∠1=∠2(已知),∴∠2=∠3(
),
∴
∥
(
),
∴∠3+∠4=180°(
)
6.如图1,点A(a,6)在第一象限,点B(0,b)在y轴负半轴上,且a,b满足:.
(1)求△AOB的面积.
(2)若线段AB与x轴相交于点C,在点C的右侧,x轴上是否存在点D,使S△ACD=S△BOC?若存在,求出D点坐标;若不存在,请说明理由.
(3)如图2,若∠AOx轴=60°,射线OA绕O点以每秒4°的速度顺时针旋转到OA′,射线OB绕B点以每秒10°的速度顺时针旋转到O′B,当OB转动一周时两者都停止运动.若两射线同时开始运动,在旋转过程中,经过多长时间,OA′∥O′B?
7.如图,在图a、图b、图c中都有直线m∥n,
(1)在图a中,∠2和∠1、∠3之间的数量关系是
.
(2)猜想:在图b中,∠1、∠2、∠3、∠4之间的数量关系是
.
(3)猜想:在图c中,∠2、∠4和∠1、∠3、∠5的数量关系式是
.
8.如图,AD平分∠BAC,∠EAD=∠EDA.
(1)求证:∠EAC=∠B;
(2)若∠B=50°,∠CAD:∠E=1:3,求∠E的度数.
9.已知:如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.试解答下列问题:
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系:
;
(2)仔细观察,在图2中“8字形”的个数:
个;
(3)在图2中,若∠D=40°,∠B=36°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.利用(1)的结论,试求∠P的度数;
(4)如果图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系.(直接写出结论即可)
10.如图所示,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E.试说明AD∥BC.完成推理过程:
∵AB∥DC(已知)
∴∠1=∠CFE(
)
∵AE平分∠BAD(已知)
∴∠1=∠2
(角平分线的定义)
∵∠CFE=∠E(已知)
∴∠2=
(等量代换)
∴AD∥BC
(
)
参考答案
1.解:(1)∵∠DBC=∠A+∠ACB,∠BCE=∠A+∠ABC,
∴∠DBC+∠BCE=180°+∠A=220°,
∵BP、CP分别是△ABC的外角∠CBD、∠BCE的角平分线,
∴∠CBP+∠BCP=(∠DBC+∠BCE)=110°,
∴∠BPC=180°﹣110°=70°,
∵BQ、CQ分别是∠PBC、∠PCB的角平分线,
∴∠QBC=∠PBC,∠QCB=∠PCB,
∴∠QBC+∠QCB=55°,
∴∠BQC=180°﹣55°=125°;
(2)∵BM∥CN,
∴∠MBC+∠NCB=180°,
∵BM、CN分别是∠PBD、∠PCE的角平分线,∠BAC=α,
∴(∠DBC+∠BCE)=180°,
即(180°+α)=180°,
解得α=60°;
(3)∵α=120°,
∴∠MBC+∠NCB=(∠DBC+∠BCE)=(180°+α)=225°,
∴∠BOC=225°﹣180°=45°;
(4)∵α>60°,
∠BPC=90°﹣α、
∠BQC=135°﹣α、
∠BOC=α﹣45°.
∠BPC、∠BQC、∠BOC三角之间的数量关系:∠BPC+∠BQC+∠BOC=(90°﹣α)+(135°﹣α)+(α﹣45°)=180°.
故答案为:70,125;60;∠BPC+∠BQC+∠BOC=180°.
2.解:(1)设∠BCD=a,则∠BDC=a+20,
∴∠CBD=180°﹣∠BCD﹣∠BDC=160﹣2a,
∵DF∥BC,
∴∠BDF=∠CBD,
∵DG平分∠BDF,
∴∠BDG=∠BDF=∠CBD=80﹣a,
∴∠GDC=∠BDG+∠BDC=80﹣a+a+20=100,
∵DH平分∠GDC,
∴∠GDH=∠GDC=50°;
(2)①∵BP平分∠ABC,DP平分∠ADE,
∴∠ABC=2∠ABP=2x,
∠ADE=2∠ADP=2z,
∵∠ACB是△DCE的外角,
∴∠E=∠ACB﹣∠CDE,
在△ABC中,∠ACB=180°﹣∠ABC﹣∠A=180°﹣2x﹣∠A,
∴∠E=180°﹣2
x﹣∠A﹣(180°﹣2z)
=﹣2x+2z﹣∠A.
∵在△ABK中,∠A=180°﹣∠ABK﹣∠AKB=180°﹣x﹣y,
∴∠E=﹣2x+2z﹣(180°﹣x﹣y)=2z﹣x+y﹣180°;
②∵∠AKP分别是△PKD与△ABK的外角,
∴∠P=∠AKP﹣∠ADP,∠AKP=∠A+∠ABK,
∴∠P=∠A+∠ABK﹣∠ADP=180°﹣y﹣z,
∴∠E=﹣2x+2z﹣(180°﹣x﹣y)=2z﹣x+y﹣180°,
∵(∠A﹣∠E)=(180°﹣x﹣y)﹣(2z﹣x+y﹣180°)=180°﹣y﹣z,
∴∠P=(∠A﹣∠E).
3.解:故答案为:
对顶角;
DMN;
同为角相等,两直线平行;
同旁内角互补;
已知;
∠D;
同旁内角互补;
两直线平行,内错角相等
4.解:(1)∠BAC=180°﹣∠B﹣∠C=180°﹣35°﹣65°=80°,
∵AD平分∠BAC,
∴∠BAD=∠BAC=40°,
∵AE⊥BC,
∴∠AEB=90°,
∴∠BAE=90°﹣∠B=55°,
∴∠DAE=∠BAE﹣∠BAD=55°﹣40°=15°;
(2)作AH⊥BC于H,如图②,
由(1)得∠DAH=15°,
∵FE⊥BC,
∴AH∥EF,
∴∠DFE=∠DAH=15°;
(3)作AH⊥BC于H,如图③,
由(1)得∠DAH=15°,
∵FE⊥BC,
∴AH∥EF,
∴∠DFE=∠DAH=15°;
(4)结合上述三个问题的解决过程,得到∠BAC的角平分线与角平分线上的点作BC的垂线的夹角为15°.
5.解:∵AD∥BC(已知),
∴∠1=∠3(两直线平行,内错角相等),
∵∠1=∠2(已知),
∴∠2=∠3(等量代换),
∴BE∥DF(同位角相等,两直线平行),
∴∠3+∠4=180°
(两直线平行,同旁内角互补).
6.解:(1)∵.
∴a﹣2=0,b+4=0,
解得a=2,b=﹣4;
∴A(2,6),B(0.﹣4)
△AOB的面积为:×4×2=4;
(2)设直线AB的关系式为y=mx+n,
∵A(2,6),B(0.﹣4),
∴,
解得,
∴直线AB的关系式为y=x﹣4,
当y=0时,x=,
∴C(,0),
设D(a,0),
∵S△ACD=S△BOC,
∴×6×(a﹣)=4××,
解得:a=,
∴D点坐标(,0);
(3)设x秒后OA′∥O′B,由题意得:
①当∠1=∠2时,(90﹣60)+4x=10x,
解得:x=5;
②当∠3=∠4时,180﹣(30+4x)=360﹣10x,
解得x=35,
答:在旋转过程中,经过5或35秒时间,OA′∥O′B.
7.解:(1)如图,过∠2的顶点作m∥a,
∵m∥n,
∴a∥m∥n,
∴∠4=∠1,∠5=∠3,
∵∠2=∠4+∠5,
∴∠2=∠1+∠3;
(2)猜想:∠2+∠4=∠1+∠3;
(3)猜想:∠2+∠4=∠1+∠3+180°﹣∠5.
故答案为:∠2=∠1+∠3;∠2+∠4=∠1+∠3;∠2+∠4=∠1+∠3+180°﹣∠5.
8.(1)证明:∵AD平分∠BAC
∴∠CAD=∠BAD=∠BAC
∵∠EDA=∠B+∠BDA,∠EAD=∠CAD+∠EAC,∠EDA=∠EAD
∴∠B=∠EAC
(2)解:由(1)可知:∠EAC=∠B=50°,
设∠CAD=x,则∠E=3x,∠EAD=∠ADE=x+50°,
∴50°+x+50°+x+3x=180°,
∴x=16°,
∴∠E=3x=48°.
9.解:(1)在△AOD中,∠AOD=180°﹣∠A﹣∠D,
在△BOC中,∠BOC=180°﹣∠B﹣∠C,
∵∠AOD=∠BOC(对顶角相等),
∴180°﹣∠A﹣∠D=180°﹣∠B﹣∠C,
∴∠A+∠D=∠B+∠C;
(2)交点有点M、O、N,
以M为交点有1个,为△AMD与△CMP,
以O为交点有4个,为△AOD与△COB,△AOM与△CON,△AOM与△COB,△CON与△AOD,
以N为交点有1个,为△ANP与△CNB,
所以,“8字形”图形共有6个;
(3)∵∠D=40°,∠B=36°,
∴∠OAD+40°=∠OCB+36°,
∴∠OCB﹣∠OAD=4°,
∵AP、CP分别是∠DAB和∠BCD的角平分线,
∴∠DAM=∠OAD,∠PCM=∠OCB,
又∵∠DAM+∠D=∠PCM+∠P,
∴∠P=∠DAM+∠D﹣∠PCM=(∠OAD﹣∠OCB)+∠D=×(﹣4°)+40°=38°;
(4)根据“8字形”数量关系,∠OAD+∠D=∠OCB+∠B,∠DAM+∠D=∠PCM+∠P,
所以,∠OCB﹣∠OAD=∠D﹣∠B,∠PCM﹣∠DAM=∠D﹣∠P,
∵AP、CP分别是∠DAB和∠BCD的角平分线,
∴∠DAM=∠OAD,∠PCM=∠OCB,
∴(∠D﹣∠B)=∠D﹣∠P,
整理得,2∠P=∠B+∠D.
10.证明:∵AB∥DC(已知)
∴∠1=∠CFE(两直线平行,同位角相等)
∵AE平分∠BAD(已知)
∴∠1=∠2(角平分线的定义)
∵∠CFE=∠E(已知)
∴∠2=∠E(等量代换)
∴AD∥BC(内错角相等,两直线平行).
故答案为:两直线平行,同位角相等;∠E;内错角相等,两直线平行.
易错题专练(三)
1.已知如图①,BP、CP分别是△ABC的外角∠CBD、∠BCE的角平分线,BQ、CQ分别是∠PBC、∠PCB的角平分线,BM、CN分别是∠PBD、∠PCE的角平分线,∠BAC=α.
(1)当α=40°时,∠BPC=
°,∠BQC=
°;
(2)当α=
°时,BM∥CN;
(3)如图②,当α=120°时,BM、CN所在直线交于点O,求∠BOC的度数;
(4)在α>60°的条件下,直接写出∠BPC、∠BQC、∠BOC三角之间的数量关系:
.
2.已知,如图,E为BC延长线上一点,点D是线段AC上一点.
(1)如图1,DF∥BC,作DG平分∠BDF交AB于G,DH平分∠GDC交BC于H,且∠BDC比∠ACB大20°,求∠GDH的度数.
(2)如图2,连接DE,若∠ABC的平分线与∠ADE的平分线相交于点P,BP交AC于点K.
①设∠ABK=x,∠AKB=y,∠ADP=z,试用x,y,z表示∠E;
②求证:∠P=(∠A﹣∠E).
3.已知:如图,∠1=∠2,∠C=∠D.
求证:∠A=∠F.
证明:∵∠1=∠2(已知),
又∠1=∠DMN(
),
∴∠2=∠
(等量代换),
∴DB∥EC(
),
∴∠DBC+∠C=180°(两直线平行,
),
∵∠C=∠D(
),
∴∠DBC+
=180°(等量代换),
∴DF∥AC(
,两直线平行),
∴∠A=∠F(
)
4.(1)如图①,△ABC中,点D、E在边BC上,AD平分∠BAC,AE⊥BC,∠B=35°,∠C=65°,求∠DAE的度数;
(2)如图②,若把(1)中的条件“AE⊥BC”变成“F为DA延长线上一点,FE⊥BC”,其它条件不变,求∠DFE的度数;
(3)若把(1)中的条件“AE⊥BC”变成“F为AD延长线上一点,FE⊥BC”,其它条件不变,请画出相应的图形,并求出∠DFE的度数;
(4)结合上述三个问题的解决过程,你能得到什么结论?
5.如图,已知AD∥BC,∠1=∠2,要证∠3+∠4=180°,请完善证明过程,并在括号内填上相应依据:
∵AD∥BC(已知),∴∠1=∠3(
),
∵∠1=∠2(已知),∴∠2=∠3(
),
∴
∥
(
),
∴∠3+∠4=180°(
)
6.如图1,点A(a,6)在第一象限,点B(0,b)在y轴负半轴上,且a,b满足:.
(1)求△AOB的面积.
(2)若线段AB与x轴相交于点C,在点C的右侧,x轴上是否存在点D,使S△ACD=S△BOC?若存在,求出D点坐标;若不存在,请说明理由.
(3)如图2,若∠AOx轴=60°,射线OA绕O点以每秒4°的速度顺时针旋转到OA′,射线OB绕B点以每秒10°的速度顺时针旋转到O′B,当OB转动一周时两者都停止运动.若两射线同时开始运动,在旋转过程中,经过多长时间,OA′∥O′B?
7.如图,在图a、图b、图c中都有直线m∥n,
(1)在图a中,∠2和∠1、∠3之间的数量关系是
.
(2)猜想:在图b中,∠1、∠2、∠3、∠4之间的数量关系是
.
(3)猜想:在图c中,∠2、∠4和∠1、∠3、∠5的数量关系式是
.
8.如图,AD平分∠BAC,∠EAD=∠EDA.
(1)求证:∠EAC=∠B;
(2)若∠B=50°,∠CAD:∠E=1:3,求∠E的度数.
9.已知:如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.试解答下列问题:
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系:
;
(2)仔细观察,在图2中“8字形”的个数:
个;
(3)在图2中,若∠D=40°,∠B=36°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.利用(1)的结论,试求∠P的度数;
(4)如果图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系.(直接写出结论即可)
10.如图所示,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E.试说明AD∥BC.完成推理过程:
∵AB∥DC(已知)
∴∠1=∠CFE(
)
∵AE平分∠BAD(已知)
∴∠1=∠2
(角平分线的定义)
∵∠CFE=∠E(已知)
∴∠2=
(等量代换)
∴AD∥BC
(
)
参考答案
1.解:(1)∵∠DBC=∠A+∠ACB,∠BCE=∠A+∠ABC,
∴∠DBC+∠BCE=180°+∠A=220°,
∵BP、CP分别是△ABC的外角∠CBD、∠BCE的角平分线,
∴∠CBP+∠BCP=(∠DBC+∠BCE)=110°,
∴∠BPC=180°﹣110°=70°,
∵BQ、CQ分别是∠PBC、∠PCB的角平分线,
∴∠QBC=∠PBC,∠QCB=∠PCB,
∴∠QBC+∠QCB=55°,
∴∠BQC=180°﹣55°=125°;
(2)∵BM∥CN,
∴∠MBC+∠NCB=180°,
∵BM、CN分别是∠PBD、∠PCE的角平分线,∠BAC=α,
∴(∠DBC+∠BCE)=180°,
即(180°+α)=180°,
解得α=60°;
(3)∵α=120°,
∴∠MBC+∠NCB=(∠DBC+∠BCE)=(180°+α)=225°,
∴∠BOC=225°﹣180°=45°;
(4)∵α>60°,
∠BPC=90°﹣α、
∠BQC=135°﹣α、
∠BOC=α﹣45°.
∠BPC、∠BQC、∠BOC三角之间的数量关系:∠BPC+∠BQC+∠BOC=(90°﹣α)+(135°﹣α)+(α﹣45°)=180°.
故答案为:70,125;60;∠BPC+∠BQC+∠BOC=180°.
2.解:(1)设∠BCD=a,则∠BDC=a+20,
∴∠CBD=180°﹣∠BCD﹣∠BDC=160﹣2a,
∵DF∥BC,
∴∠BDF=∠CBD,
∵DG平分∠BDF,
∴∠BDG=∠BDF=∠CBD=80﹣a,
∴∠GDC=∠BDG+∠BDC=80﹣a+a+20=100,
∵DH平分∠GDC,
∴∠GDH=∠GDC=50°;
(2)①∵BP平分∠ABC,DP平分∠ADE,
∴∠ABC=2∠ABP=2x,
∠ADE=2∠ADP=2z,
∵∠ACB是△DCE的外角,
∴∠E=∠ACB﹣∠CDE,
在△ABC中,∠ACB=180°﹣∠ABC﹣∠A=180°﹣2x﹣∠A,
∴∠E=180°﹣2
x﹣∠A﹣(180°﹣2z)
=﹣2x+2z﹣∠A.
∵在△ABK中,∠A=180°﹣∠ABK﹣∠AKB=180°﹣x﹣y,
∴∠E=﹣2x+2z﹣(180°﹣x﹣y)=2z﹣x+y﹣180°;
②∵∠AKP分别是△PKD与△ABK的外角,
∴∠P=∠AKP﹣∠ADP,∠AKP=∠A+∠ABK,
∴∠P=∠A+∠ABK﹣∠ADP=180°﹣y﹣z,
∴∠E=﹣2x+2z﹣(180°﹣x﹣y)=2z﹣x+y﹣180°,
∵(∠A﹣∠E)=(180°﹣x﹣y)﹣(2z﹣x+y﹣180°)=180°﹣y﹣z,
∴∠P=(∠A﹣∠E).
3.解:故答案为:
对顶角;
DMN;
同为角相等,两直线平行;
同旁内角互补;
已知;
∠D;
同旁内角互补;
两直线平行,内错角相等
4.解:(1)∠BAC=180°﹣∠B﹣∠C=180°﹣35°﹣65°=80°,
∵AD平分∠BAC,
∴∠BAD=∠BAC=40°,
∵AE⊥BC,
∴∠AEB=90°,
∴∠BAE=90°﹣∠B=55°,
∴∠DAE=∠BAE﹣∠BAD=55°﹣40°=15°;
(2)作AH⊥BC于H,如图②,
由(1)得∠DAH=15°,
∵FE⊥BC,
∴AH∥EF,
∴∠DFE=∠DAH=15°;
(3)作AH⊥BC于H,如图③,
由(1)得∠DAH=15°,
∵FE⊥BC,
∴AH∥EF,
∴∠DFE=∠DAH=15°;
(4)结合上述三个问题的解决过程,得到∠BAC的角平分线与角平分线上的点作BC的垂线的夹角为15°.
5.解:∵AD∥BC(已知),
∴∠1=∠3(两直线平行,内错角相等),
∵∠1=∠2(已知),
∴∠2=∠3(等量代换),
∴BE∥DF(同位角相等,两直线平行),
∴∠3+∠4=180°
(两直线平行,同旁内角互补).
6.解:(1)∵.
∴a﹣2=0,b+4=0,
解得a=2,b=﹣4;
∴A(2,6),B(0.﹣4)
△AOB的面积为:×4×2=4;
(2)设直线AB的关系式为y=mx+n,
∵A(2,6),B(0.﹣4),
∴,
解得,
∴直线AB的关系式为y=x﹣4,
当y=0时,x=,
∴C(,0),
设D(a,0),
∵S△ACD=S△BOC,
∴×6×(a﹣)=4××,
解得:a=,
∴D点坐标(,0);
(3)设x秒后OA′∥O′B,由题意得:
①当∠1=∠2时,(90﹣60)+4x=10x,
解得:x=5;
②当∠3=∠4时,180﹣(30+4x)=360﹣10x,
解得x=35,
答:在旋转过程中,经过5或35秒时间,OA′∥O′B.
7.解:(1)如图,过∠2的顶点作m∥a,
∵m∥n,
∴a∥m∥n,
∴∠4=∠1,∠5=∠3,
∵∠2=∠4+∠5,
∴∠2=∠1+∠3;
(2)猜想:∠2+∠4=∠1+∠3;
(3)猜想:∠2+∠4=∠1+∠3+180°﹣∠5.
故答案为:∠2=∠1+∠3;∠2+∠4=∠1+∠3;∠2+∠4=∠1+∠3+180°﹣∠5.
8.(1)证明:∵AD平分∠BAC
∴∠CAD=∠BAD=∠BAC
∵∠EDA=∠B+∠BDA,∠EAD=∠CAD+∠EAC,∠EDA=∠EAD
∴∠B=∠EAC
(2)解:由(1)可知:∠EAC=∠B=50°,
设∠CAD=x,则∠E=3x,∠EAD=∠ADE=x+50°,
∴50°+x+50°+x+3x=180°,
∴x=16°,
∴∠E=3x=48°.
9.解:(1)在△AOD中,∠AOD=180°﹣∠A﹣∠D,
在△BOC中,∠BOC=180°﹣∠B﹣∠C,
∵∠AOD=∠BOC(对顶角相等),
∴180°﹣∠A﹣∠D=180°﹣∠B﹣∠C,
∴∠A+∠D=∠B+∠C;
(2)交点有点M、O、N,
以M为交点有1个,为△AMD与△CMP,
以O为交点有4个,为△AOD与△COB,△AOM与△CON,△AOM与△COB,△CON与△AOD,
以N为交点有1个,为△ANP与△CNB,
所以,“8字形”图形共有6个;
(3)∵∠D=40°,∠B=36°,
∴∠OAD+40°=∠OCB+36°,
∴∠OCB﹣∠OAD=4°,
∵AP、CP分别是∠DAB和∠BCD的角平分线,
∴∠DAM=∠OAD,∠PCM=∠OCB,
又∵∠DAM+∠D=∠PCM+∠P,
∴∠P=∠DAM+∠D﹣∠PCM=(∠OAD﹣∠OCB)+∠D=×(﹣4°)+40°=38°;
(4)根据“8字形”数量关系,∠OAD+∠D=∠OCB+∠B,∠DAM+∠D=∠PCM+∠P,
所以,∠OCB﹣∠OAD=∠D﹣∠B,∠PCM﹣∠DAM=∠D﹣∠P,
∵AP、CP分别是∠DAB和∠BCD的角平分线,
∴∠DAM=∠OAD,∠PCM=∠OCB,
∴(∠D﹣∠B)=∠D﹣∠P,
整理得,2∠P=∠B+∠D.
10.证明:∵AB∥DC(已知)
∴∠1=∠CFE(两直线平行,同位角相等)
∵AE平分∠BAD(已知)
∴∠1=∠2(角平分线的定义)
∵∠CFE=∠E(已知)
∴∠2=∠E(等量代换)
∴AD∥BC(内错角相等,两直线平行).
故答案为:两直线平行,同位角相等;∠E;内错角相等,两直线平行.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
