2020-2021学年人教版数学九年级下册第27章《相似》常考题专练(四)(Word版 含解析)
文档属性
| 名称 | 2020-2021学年人教版数学九年级下册第27章《相似》常考题专练(四)(Word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 188.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-21 22:28:27 | ||
图片预览



文档简介
人教版数学九年级下册第27章《相似》
常考题专练(四)
1.为了测量路灯(OS)的高度,把一根长1.5米的竹竿(AB)竖直立在水平地面上,测得竹竿的影子(BC)长为1米,然后拿竹竿向远离路灯方向走了4米(BB′),再把竹竿竖立在地面上,测得竹竿的影长(B′C′)为1.8米,求路灯离地面的高度.
2.阅读下面的短文,并回答下列问题
我们把相似形的概念推广到空间:如果两个几何体大小不一定相等,但形状完全相同,就把它们叫做相似体.
如图,甲、乙是两个不同的立方体,立方体都是相似体,它们的一切对应线段之比都等于相似比(a:b).
设S甲、S乙分别表示这两个立方体的表面积,则,又设V甲、V乙分别表示这两个立方体的体积,则.
(1)下列几何体中,一定属于相似体的是
A、两个球体B、两个圆锥体C、两个圆柱体D、两个长方体.
(2)请归纳出相似体的三条主要性质:
①相似体的一切对应线段(或弧)长度的比等于
;
②相似体表面积的比等于
;
③相似体体积的比等于
.
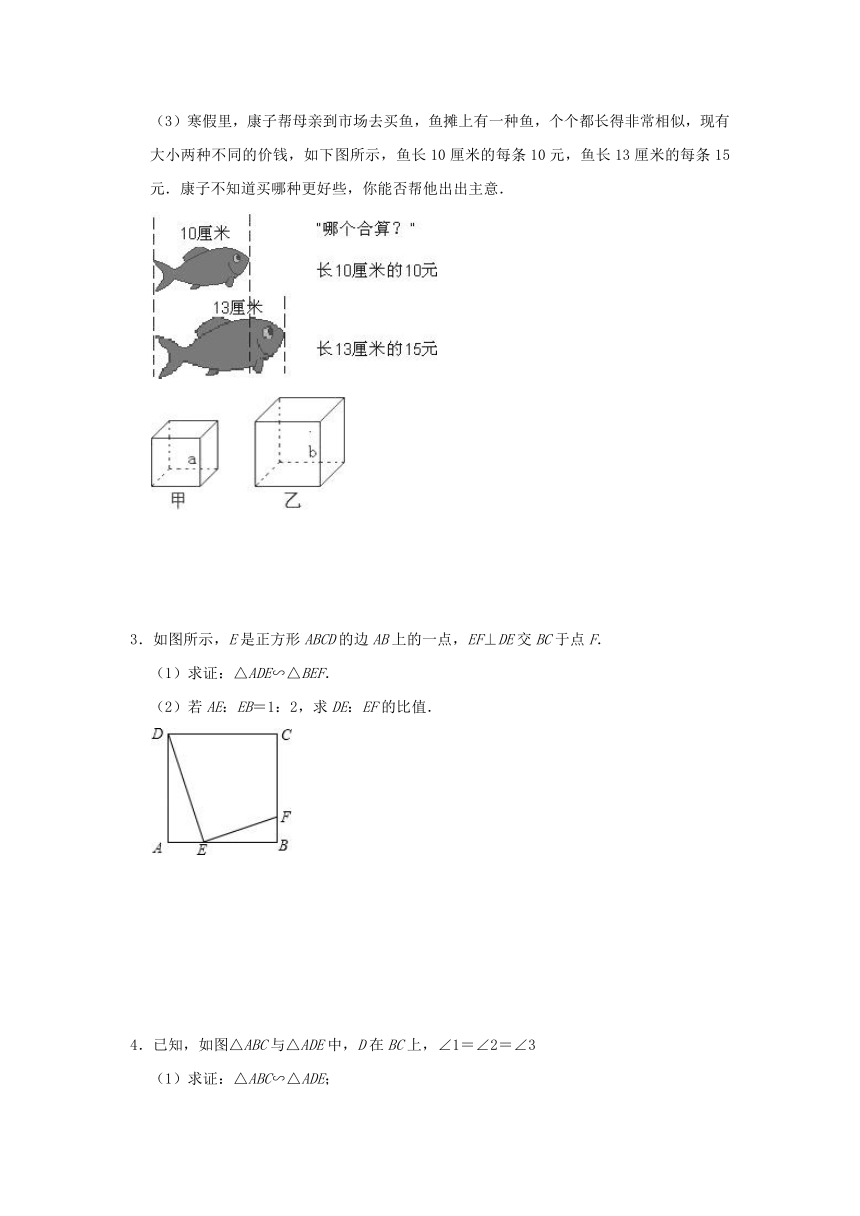
(3)寒假里,康子帮母亲到市场去买鱼,鱼摊上有一种鱼,个个都长得非常相似,现有大小两种不同的价钱,如下图所示,鱼长10厘米的每条10元,鱼长13厘米的每条15元.康子不知道买哪种更好些,你能否帮他出出主意.
3.如图所示,E是正方形ABCD的边AB上的一点,EF⊥DE交BC于点F.
(1)求证:△ADE∽△BEF.
(2)若AE:EB=1:2,求DE:EF的比值.
4.已知,如图△ABC与△ADE中,D在BC上,∠1=∠2=∠3
(1)求证:△ABC∽△ADE;
(2)若AB=4,AD=2,AC=3,求AE的长.
5.如图所示,
(1)正方形ABCD及等腰Rt△AEF有公共顶点A,∠EAF=90°,连接BE、DF.将Rt△AEF绕点A旋转,在旋转过程中,BE、DF具有怎样的数量关系和位置关系?结合图(1)给予证明;
(2)将(1)中的正方形ABCD变为矩形ABCD,等腰Rt△AEF变为Rt△AEF,且AD=kAB,AF=kAE,其他条件不变.(1)中的结论是否发生变化?结合图(2)说明理由;
(3)将(2)中的矩形ABCD变为平行四边形ABCD,将Rt△AEF变为△AEF,且∠BAD=∠EAF=a,其他条件不变.(2)中的结论是否发生变化?结合图(3),如果不变,直接写出结论;如果变化,直接用k表示出线段BE、DF的数量关系,用a表示出直线BE、DF形成的锐角β.
6.如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.你能利用小明测量的数据算出电线杆AB的高吗?
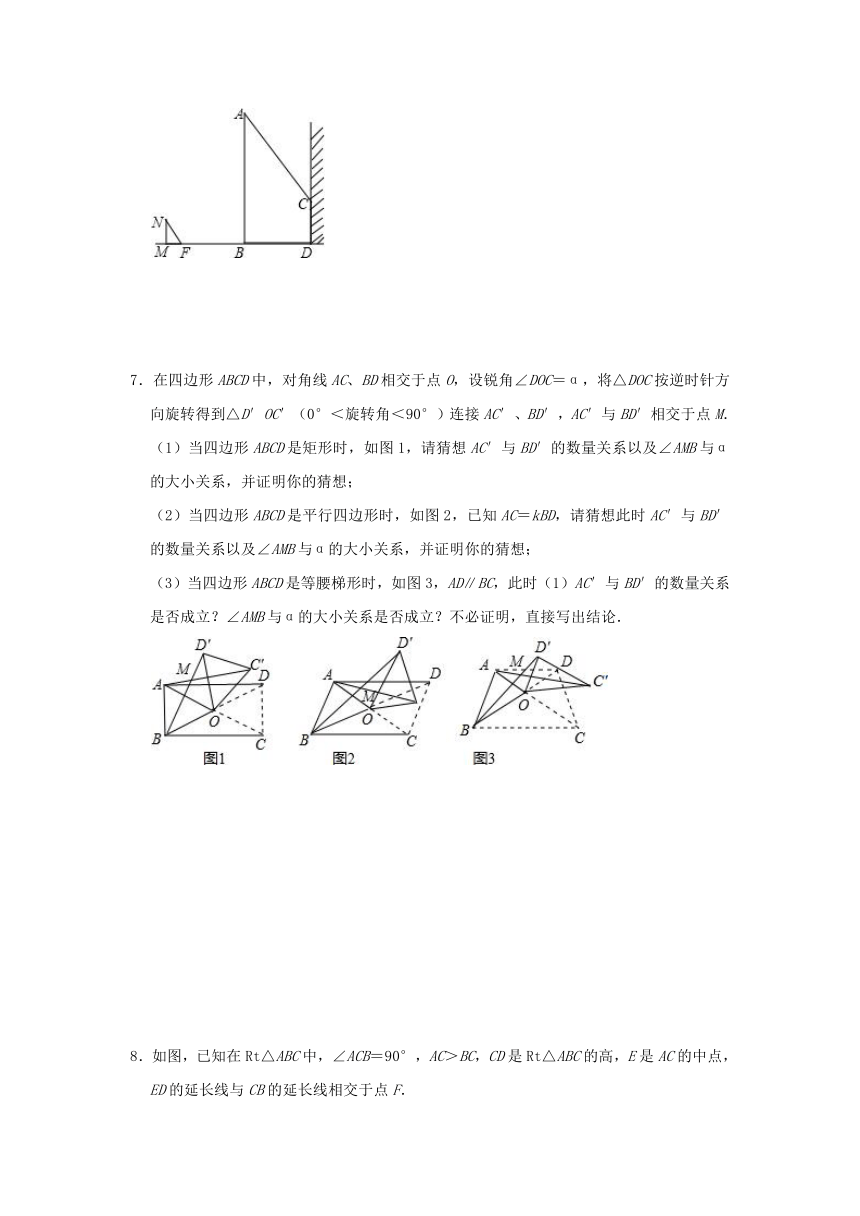
7.在四边形ABCD中,对角线AC、BD相交于点O,设锐角∠DOC=α,将△DOC按逆时针方向旋转得到△D′OC′(0°<旋转角<90°)连接AC′、BD′,AC′与BD′相交于点M.
(1)当四边形ABCD是矩形时,如图1,请猜想AC′与BD′的数量关系以及∠AMB与α的大小关系,并证明你的猜想;
(2)当四边形ABCD是平行四边形时,如图2,已知AC=kBD,请猜想此时AC′与BD′的数量关系以及∠AMB与α的大小关系,并证明你的猜想;
(3)当四边形ABCD是等腰梯形时,如图3,AD∥BC,此时(1)AC′与BD′的数量关系是否成立?∠AMB与α的大小关系是否成立?不必证明,直接写出结论.
8.如图,已知在Rt△ABC中,∠ACB=90°,AC>BC,CD是Rt△ABC的高,E是AC的中点,ED的延长线与CB的延长线相交于点F.
(1)求证:DF是BF和CF的比例中项;
(2)在AB上取一点G,如果AE?AC=AG?AD,求证:EG?CF=ED?DF.
9.在Rt△ABC中,∠C=90°,BC=6cm,∠ABC=30°.D是CB上一点,DC=1cm.P、Q是直线CB上的两个动点,点P从C点出发,以1cm/s的速度沿直线CB向右运动,同时,点Q从D点出发,以2cm/s的速度沿直线CB向右运动,以PQ为一边在CB的上方作等边三角形PQR,下图是其运动过程中的某一位置.设运动的时间是t(s).
(1)△PQR的边长是
cm(用含有t的代数式表示);
(2)若等边△PQR与△ABC重叠部分的面积为y(cm2),求y与t之间的函数关系式,并写出自变量t的取值范围.
10.在等腰梯形ABCD中,AD∥BC,AD=3,AB=CD=4,BC=5,∠B的平分线交DC于点E,交AD的延长线于点F.
(1)如图(1),若∠C的平分线交BE于点G,写出图中所有的相似三角形(不必证明);
(2)在(1)的条件下求BG的长;
(3)若点P为BE上动点,以点P为圆心,BP为半径的⊙P与线段BC交于点Q(如图(2)),请直接写出当BP取什么范围内值时,①点A在⊙P内;②点A在⊙P内而点E在⊙P外.
参考答案
1.解:∵AB⊥OC′,OS⊥OC′,
∴SO∥AB,
∴△ABC∽△SOC,
∴=,即=,
解得OB=h﹣1①,
同理,∵A′B′⊥OC′,
∴△A′B′C′∽△SOC′,
∴=,=②,
把①代入②得,=,
解得h=9(米).
答:路灯离地面的高度是9米.
2.解:(1)A
(2)相似比;相似比的平方;相似比的立方
(3)因为同一种鱼的密度一样,所以它们的质量比等于体积比
设这两种鱼的质量分别为m、M,则有
而它们的价格比为15:10=1.5,∴买15元一条的鱼更合算.
3.(1)证明:∵ABCD是正方形,
∴∠DAE=∠FBE=90°,
∴∠ADE+∠DEA=90°,
又∵EF⊥DE,
∴∠AED+∠FEB=90°,
∴∠ADE=∠FEB,
∴△ADE∽△BEF.
(2)解:∵AE:EB=1:2,
∴EB:AB=2:3,
∵AD=AB,
∴EB:AD=2:3,
∵△ADE∽△BEF,
∴DE:EF=AD:EB=3:2.
4.(1)证明:∵△ABC与△ADE中,D在BC上,∠2=∠3,
∴∠E=∠C,
∵∠DAE=∠DAC+∠2,∠BAC=∠DAC+∠1,
∵∠1=∠2,
∴∠DAE=∠BAC,
∵∠1=∠3,
∴∠B=∠ADE,
∴△ABC∽△ADE;
(2)解:∵△ABC∽△ADE(已证);
∴=,
∵AB=4,AD=2,AC=3,
∴=,
∴AE=1.5.
答:AE的长为1.5.
5.解:(1)DF与BE互相垂直且相等.
证明:延长DF分别交AB、BE于点P、G(1分)
在正方形ABCD和等腰直角△AEF中
AD=AB,AF=AE,
∠BAD=∠EAF=90°
∴∠FAD=∠EAB
∴△FAD≌△EAB(2分)
∴∠AFD=∠AEB,DF=BE(3分)
∵∠AFD+∠AFG=180°,
∴∠AEG+∠AFG=180°,
∵∠EAF=90°,
∴∠EGF=180°﹣90°=90°,
∴DF⊥BE(5分)
(2)数量关系改变,位置关系不变.DF=kBE,DF⊥BE.(7分)
延长DF交EB于点H,
∵AD=kAB,AF=kAE
∴=k,=k
∴=
∵∠BAD=∠EAF=90°,
∴∠FAD=∠EAB
∴△FAD∽△EAB(9分)
∴=k
∴DF=kBE(10分)
∵△FAD∽△EAB,
∴∠AFD=∠AEB,
∵∠AFD+∠AFH=180°,
∴∠AEH+∠AFH=180°,
∵∠EAF=90°,
∴∠EHF=180°﹣90°=90°,
∴DF⊥BE(5分)
(3)不改变.DF=kBE,β=180°﹣a.(7分)
证法(一):延长DF交EB的延长线于点H,
∵AD=kAB,AF=kAE
∴=k,=k
∴=
∵∠BAD=∠EAF=a
∴∠FAD=∠EAB
∴△FAD∽△EAB(9分)
∴=k
∴DF=kBE(10分)
由△FAD∽△EAB得∠AFD=∠AEB
∵∠AFD+∠AFH=180°
∴∠AEB+∠AFH=180°
∵四边形AEHF的内角和为360°,
∴∠EAF+∠EHF=180°
∵∠EAF=α,∠EHF=β
∴a+β=180°∴β=180°﹣a(12分)
证法(二):DF=kBE的证法与证法(一)相同
延长DF分别交EB、AB的延长线于点H、G.由△FAD∽△EAB得∠ADF=∠ABE
∵∠ABE=∠GBH,∴∠ADF=∠GBH,
∵β=∠BHF=∠GBH+∠G∴β=∠ADF+∠G.
在△ADG中,∠BAD+∠ADF+∠G=180°,∠BAD=a
∴a+β=180°∴β=180°﹣a(12分)
证法(三):在平行四边形ABCD中AB∥CD可得到∠ABC+∠C=180°
∵∠EBA+∠ABC+∠CBH=180°∴∠C=∠EBA+∠CBH
在△BHP、△CDP中,由三角形内角和等于180°可得∠C+∠CDP=∠CBH+∠BHP
∴∠EBA+∠CBH+∠CDP=∠CBH+∠BHP
∴∠EBA+∠CDP=∠BHP
由△FAD∽△EAB得∠ADP=∠EBA
∴∠ADP+∠CDP=∠BHP即∠ADC=∠BHP
∵∠BAD+∠ADC=180°,∠BAD=a,∠BHP=β
∴a+β=180°∴β=180°﹣a(12分)
(有不同解法,参照以上给分点,只要正确均得分.)
6.解:过C点作CG⊥AB于点G,
∴GC=BD=3米,GB=CD=2米.
∵∠NMF=∠AGC=90°,NF∥AC,
∴∠NFM=∠ACG,
∴△NMF∽△AGC,
∴,
∴AG===6,
∴AB=AG+GB=6+2=8(米),故电线杆子的高为8米.
7.解:(1)AC′=BD′,∠AMB=α,
证明:在矩形ABCD中,AC=BD,OA=OC=AC,OB=OD=BD,
∴OA=OC=OB=OD,
又∵OD=OD′,OC=OC′,
∴OB=OD′=OA=OC′,
∵∠D′OD=∠C′OC,
∴180°﹣∠D′OD=180°﹣∠C′OC,
∴∠BOD′=∠AOC′,
∴△BOD′≌△AOC′,
∴BD′=AC′,
∴∠OBD′=∠OAC′,
设BD′与OA相交于点N,
∴∠BNO=∠ANM,
∴180°﹣∠OAC′﹣∠ANM=180°﹣∠OBD′﹣∠BNO,
即∠AMB=∠AOB=∠COD=α,
综上所述,BD′=AC′,∠AMB=α,
(2)AC′=kBD′,∠AMB=α,
证明:∵在平行四边形ABCD中,OB=OD,OA=OC,
又∵OD=OD′,OC=OC′,
∴OC′=OA,OD′=OB,
∵∠D′OD=∠C′OC,
∴180°﹣∠D′OD=180°﹣∠C′OC,
∴∠BOD′=∠AOC′,
∴△BOD′∽△AOC′,
∴BD′:AC′=OB:OA=BD:AC,
∵AC=kBD,
∴AC′=kBD′,
∵△BOD′∽△AOC′,
设BD′与OA相交于点N,
∴∠BNO=∠ANM,
∴180°﹣∠OAC′﹣∠ANM=180°﹣∠OBD′﹣∠BNO,即∠AMB=∠AOB=α,
综上所述,AC′=kBD′,∠AMB=α,
(3)AC′=BD′成立,∠AMB=α不成立.
8.证明:(1)∵∠ACB=90°,CD⊥AB,
∴∠BCD=∠A,∠ADC=90°.
∵E是AC的中点,
∴DE=AE=CE,
∴∠ADE=∠A,
∴∠BCD=∠ADE.
又∠ADE=∠FDB,
∴∠FCD=∠FDB.
∵∠CFD=∠DFB,
∴△CFD∽△DFB,
∴DF2=BF?CF.
(2)∵AE?AC=AG?AD,
∴=.
∵∠A=∠A,
∴△AEG∽△ADC,
∴EG∥BC,
∴△EGD∽△FBD,
∴=.
由(1)知:△CFD∽△DFB,
∴=,
∴=,
∴EG?CF=ED?DF.
9.解:(1)△PQR的边长PQ=CQ﹣CP=(CD+DP)﹣CP=(1+2t)﹣t=(t+1)cm;
故答案为:(t+1);
(2)当0≤t<时,如图1:易得重叠部分为一个小等边三角形其边长为t+1,
则重叠部分的面积y=(t+1)2;(5分)
当≤t<时,如图2:易得重叠部分为四边形MNQP,
∵∠B=30°,且△RPQ为等边三角形,得到∠RPQ=∠R=60°,
∴∠PMN=90°,且PB=BC﹣CP=6﹣t,∠RNM=30°,
∴PM=(6﹣t),故MR=PR﹣PM=(t+1)﹣(6﹣t)=(3t﹣4),
∴MN=MR?tan60°=(3t﹣4),
则重叠部分的面积y=(t+1)2﹣(3t﹣4)2
=﹣t2+t﹣
=﹣(t﹣2)2+;(8分)
当≤t<6时,如图3:同理可得y=(6﹣t)2;(11分)
当t≥6时,如图4:可得y=0.(12分)
10.解:(1)△ABF∽△GBC,△FDE∽△CGE∽△BCE.
(2)∵BE平分∠B,
∴∠ABE=∠EBC,
∵AD∥BC,
∴∠AFB=∠EBC,
∴∠ABE=∠AFB,
∴AB=AF.
∴AF=4,DF=1.
∵AD∥BC,
∴DF:BC=DE:EC,
∴DE=,CE=.
∵AD∥BC,AB=CD,
∴∠BCD=∠ABC.
∵CG平分∠BCD,BE平分∠ABC,
∴∠CBG=∠BCG,
∴BG=CG.
设BG=CG=x,则由△FDE∽△CGE,得
DF:CG=DE:GE,
∴GE=x.
又由△CGE∽△BCE,得
EC2=EG?EB,
即=x?(x+x),
∴x=,
即BG=.
(3)①连接AP,当BP=AP时,点A在圆P上,此时△ABP∽△ABF,求得BP=,
即BP>AP时,点A在⊙P内.
∴当<BP≤时,点A在⊙P内.
②根据①求得BE=,
∴BP<BE,即BP<时,点A在⊙P内而点E在⊙P外
∴当<BP<时,点A在⊙P内而点E在⊙P外.
常考题专练(四)
1.为了测量路灯(OS)的高度,把一根长1.5米的竹竿(AB)竖直立在水平地面上,测得竹竿的影子(BC)长为1米,然后拿竹竿向远离路灯方向走了4米(BB′),再把竹竿竖立在地面上,测得竹竿的影长(B′C′)为1.8米,求路灯离地面的高度.
2.阅读下面的短文,并回答下列问题
我们把相似形的概念推广到空间:如果两个几何体大小不一定相等,但形状完全相同,就把它们叫做相似体.
如图,甲、乙是两个不同的立方体,立方体都是相似体,它们的一切对应线段之比都等于相似比(a:b).
设S甲、S乙分别表示这两个立方体的表面积,则,又设V甲、V乙分别表示这两个立方体的体积,则.
(1)下列几何体中,一定属于相似体的是
A、两个球体B、两个圆锥体C、两个圆柱体D、两个长方体.
(2)请归纳出相似体的三条主要性质:
①相似体的一切对应线段(或弧)长度的比等于
;
②相似体表面积的比等于
;
③相似体体积的比等于
.
(3)寒假里,康子帮母亲到市场去买鱼,鱼摊上有一种鱼,个个都长得非常相似,现有大小两种不同的价钱,如下图所示,鱼长10厘米的每条10元,鱼长13厘米的每条15元.康子不知道买哪种更好些,你能否帮他出出主意.
3.如图所示,E是正方形ABCD的边AB上的一点,EF⊥DE交BC于点F.
(1)求证:△ADE∽△BEF.
(2)若AE:EB=1:2,求DE:EF的比值.
4.已知,如图△ABC与△ADE中,D在BC上,∠1=∠2=∠3
(1)求证:△ABC∽△ADE;
(2)若AB=4,AD=2,AC=3,求AE的长.
5.如图所示,
(1)正方形ABCD及等腰Rt△AEF有公共顶点A,∠EAF=90°,连接BE、DF.将Rt△AEF绕点A旋转,在旋转过程中,BE、DF具有怎样的数量关系和位置关系?结合图(1)给予证明;
(2)将(1)中的正方形ABCD变为矩形ABCD,等腰Rt△AEF变为Rt△AEF,且AD=kAB,AF=kAE,其他条件不变.(1)中的结论是否发生变化?结合图(2)说明理由;
(3)将(2)中的矩形ABCD变为平行四边形ABCD,将Rt△AEF变为△AEF,且∠BAD=∠EAF=a,其他条件不变.(2)中的结论是否发生变化?结合图(3),如果不变,直接写出结论;如果变化,直接用k表示出线段BE、DF的数量关系,用a表示出直线BE、DF形成的锐角β.
6.如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.你能利用小明测量的数据算出电线杆AB的高吗?
7.在四边形ABCD中,对角线AC、BD相交于点O,设锐角∠DOC=α,将△DOC按逆时针方向旋转得到△D′OC′(0°<旋转角<90°)连接AC′、BD′,AC′与BD′相交于点M.
(1)当四边形ABCD是矩形时,如图1,请猜想AC′与BD′的数量关系以及∠AMB与α的大小关系,并证明你的猜想;
(2)当四边形ABCD是平行四边形时,如图2,已知AC=kBD,请猜想此时AC′与BD′的数量关系以及∠AMB与α的大小关系,并证明你的猜想;
(3)当四边形ABCD是等腰梯形时,如图3,AD∥BC,此时(1)AC′与BD′的数量关系是否成立?∠AMB与α的大小关系是否成立?不必证明,直接写出结论.
8.如图,已知在Rt△ABC中,∠ACB=90°,AC>BC,CD是Rt△ABC的高,E是AC的中点,ED的延长线与CB的延长线相交于点F.
(1)求证:DF是BF和CF的比例中项;
(2)在AB上取一点G,如果AE?AC=AG?AD,求证:EG?CF=ED?DF.
9.在Rt△ABC中,∠C=90°,BC=6cm,∠ABC=30°.D是CB上一点,DC=1cm.P、Q是直线CB上的两个动点,点P从C点出发,以1cm/s的速度沿直线CB向右运动,同时,点Q从D点出发,以2cm/s的速度沿直线CB向右运动,以PQ为一边在CB的上方作等边三角形PQR,下图是其运动过程中的某一位置.设运动的时间是t(s).
(1)△PQR的边长是
cm(用含有t的代数式表示);
(2)若等边△PQR与△ABC重叠部分的面积为y(cm2),求y与t之间的函数关系式,并写出自变量t的取值范围.
10.在等腰梯形ABCD中,AD∥BC,AD=3,AB=CD=4,BC=5,∠B的平分线交DC于点E,交AD的延长线于点F.
(1)如图(1),若∠C的平分线交BE于点G,写出图中所有的相似三角形(不必证明);
(2)在(1)的条件下求BG的长;
(3)若点P为BE上动点,以点P为圆心,BP为半径的⊙P与线段BC交于点Q(如图(2)),请直接写出当BP取什么范围内值时,①点A在⊙P内;②点A在⊙P内而点E在⊙P外.
参考答案
1.解:∵AB⊥OC′,OS⊥OC′,
∴SO∥AB,
∴△ABC∽△SOC,
∴=,即=,
解得OB=h﹣1①,
同理,∵A′B′⊥OC′,
∴△A′B′C′∽△SOC′,
∴=,=②,
把①代入②得,=,
解得h=9(米).
答:路灯离地面的高度是9米.
2.解:(1)A
(2)相似比;相似比的平方;相似比的立方
(3)因为同一种鱼的密度一样,所以它们的质量比等于体积比
设这两种鱼的质量分别为m、M,则有
而它们的价格比为15:10=1.5,∴买15元一条的鱼更合算.
3.(1)证明:∵ABCD是正方形,
∴∠DAE=∠FBE=90°,
∴∠ADE+∠DEA=90°,
又∵EF⊥DE,
∴∠AED+∠FEB=90°,
∴∠ADE=∠FEB,
∴△ADE∽△BEF.
(2)解:∵AE:EB=1:2,
∴EB:AB=2:3,
∵AD=AB,
∴EB:AD=2:3,
∵△ADE∽△BEF,
∴DE:EF=AD:EB=3:2.
4.(1)证明:∵△ABC与△ADE中,D在BC上,∠2=∠3,
∴∠E=∠C,
∵∠DAE=∠DAC+∠2,∠BAC=∠DAC+∠1,
∵∠1=∠2,
∴∠DAE=∠BAC,
∵∠1=∠3,
∴∠B=∠ADE,
∴△ABC∽△ADE;
(2)解:∵△ABC∽△ADE(已证);
∴=,
∵AB=4,AD=2,AC=3,
∴=,
∴AE=1.5.
答:AE的长为1.5.
5.解:(1)DF与BE互相垂直且相等.
证明:延长DF分别交AB、BE于点P、G(1分)
在正方形ABCD和等腰直角△AEF中
AD=AB,AF=AE,
∠BAD=∠EAF=90°
∴∠FAD=∠EAB
∴△FAD≌△EAB(2分)
∴∠AFD=∠AEB,DF=BE(3分)
∵∠AFD+∠AFG=180°,
∴∠AEG+∠AFG=180°,
∵∠EAF=90°,
∴∠EGF=180°﹣90°=90°,
∴DF⊥BE(5分)
(2)数量关系改变,位置关系不变.DF=kBE,DF⊥BE.(7分)
延长DF交EB于点H,
∵AD=kAB,AF=kAE
∴=k,=k
∴=
∵∠BAD=∠EAF=90°,
∴∠FAD=∠EAB
∴△FAD∽△EAB(9分)
∴=k
∴DF=kBE(10分)
∵△FAD∽△EAB,
∴∠AFD=∠AEB,
∵∠AFD+∠AFH=180°,
∴∠AEH+∠AFH=180°,
∵∠EAF=90°,
∴∠EHF=180°﹣90°=90°,
∴DF⊥BE(5分)
(3)不改变.DF=kBE,β=180°﹣a.(7分)
证法(一):延长DF交EB的延长线于点H,
∵AD=kAB,AF=kAE
∴=k,=k
∴=
∵∠BAD=∠EAF=a
∴∠FAD=∠EAB
∴△FAD∽△EAB(9分)
∴=k
∴DF=kBE(10分)
由△FAD∽△EAB得∠AFD=∠AEB
∵∠AFD+∠AFH=180°
∴∠AEB+∠AFH=180°
∵四边形AEHF的内角和为360°,
∴∠EAF+∠EHF=180°
∵∠EAF=α,∠EHF=β
∴a+β=180°∴β=180°﹣a(12分)
证法(二):DF=kBE的证法与证法(一)相同
延长DF分别交EB、AB的延长线于点H、G.由△FAD∽△EAB得∠ADF=∠ABE
∵∠ABE=∠GBH,∴∠ADF=∠GBH,
∵β=∠BHF=∠GBH+∠G∴β=∠ADF+∠G.
在△ADG中,∠BAD+∠ADF+∠G=180°,∠BAD=a
∴a+β=180°∴β=180°﹣a(12分)
证法(三):在平行四边形ABCD中AB∥CD可得到∠ABC+∠C=180°
∵∠EBA+∠ABC+∠CBH=180°∴∠C=∠EBA+∠CBH
在△BHP、△CDP中,由三角形内角和等于180°可得∠C+∠CDP=∠CBH+∠BHP
∴∠EBA+∠CBH+∠CDP=∠CBH+∠BHP
∴∠EBA+∠CDP=∠BHP
由△FAD∽△EAB得∠ADP=∠EBA
∴∠ADP+∠CDP=∠BHP即∠ADC=∠BHP
∵∠BAD+∠ADC=180°,∠BAD=a,∠BHP=β
∴a+β=180°∴β=180°﹣a(12分)
(有不同解法,参照以上给分点,只要正确均得分.)
6.解:过C点作CG⊥AB于点G,
∴GC=BD=3米,GB=CD=2米.
∵∠NMF=∠AGC=90°,NF∥AC,
∴∠NFM=∠ACG,
∴△NMF∽△AGC,
∴,
∴AG===6,
∴AB=AG+GB=6+2=8(米),故电线杆子的高为8米.
7.解:(1)AC′=BD′,∠AMB=α,
证明:在矩形ABCD中,AC=BD,OA=OC=AC,OB=OD=BD,
∴OA=OC=OB=OD,
又∵OD=OD′,OC=OC′,
∴OB=OD′=OA=OC′,
∵∠D′OD=∠C′OC,
∴180°﹣∠D′OD=180°﹣∠C′OC,
∴∠BOD′=∠AOC′,
∴△BOD′≌△AOC′,
∴BD′=AC′,
∴∠OBD′=∠OAC′,
设BD′与OA相交于点N,
∴∠BNO=∠ANM,
∴180°﹣∠OAC′﹣∠ANM=180°﹣∠OBD′﹣∠BNO,
即∠AMB=∠AOB=∠COD=α,
综上所述,BD′=AC′,∠AMB=α,
(2)AC′=kBD′,∠AMB=α,
证明:∵在平行四边形ABCD中,OB=OD,OA=OC,
又∵OD=OD′,OC=OC′,
∴OC′=OA,OD′=OB,
∵∠D′OD=∠C′OC,
∴180°﹣∠D′OD=180°﹣∠C′OC,
∴∠BOD′=∠AOC′,
∴△BOD′∽△AOC′,
∴BD′:AC′=OB:OA=BD:AC,
∵AC=kBD,
∴AC′=kBD′,
∵△BOD′∽△AOC′,
设BD′与OA相交于点N,
∴∠BNO=∠ANM,
∴180°﹣∠OAC′﹣∠ANM=180°﹣∠OBD′﹣∠BNO,即∠AMB=∠AOB=α,
综上所述,AC′=kBD′,∠AMB=α,
(3)AC′=BD′成立,∠AMB=α不成立.
8.证明:(1)∵∠ACB=90°,CD⊥AB,
∴∠BCD=∠A,∠ADC=90°.
∵E是AC的中点,
∴DE=AE=CE,
∴∠ADE=∠A,
∴∠BCD=∠ADE.
又∠ADE=∠FDB,
∴∠FCD=∠FDB.
∵∠CFD=∠DFB,
∴△CFD∽△DFB,
∴DF2=BF?CF.
(2)∵AE?AC=AG?AD,
∴=.
∵∠A=∠A,
∴△AEG∽△ADC,
∴EG∥BC,
∴△EGD∽△FBD,
∴=.
由(1)知:△CFD∽△DFB,
∴=,
∴=,
∴EG?CF=ED?DF.
9.解:(1)△PQR的边长PQ=CQ﹣CP=(CD+DP)﹣CP=(1+2t)﹣t=(t+1)cm;
故答案为:(t+1);
(2)当0≤t<时,如图1:易得重叠部分为一个小等边三角形其边长为t+1,
则重叠部分的面积y=(t+1)2;(5分)
当≤t<时,如图2:易得重叠部分为四边形MNQP,
∵∠B=30°,且△RPQ为等边三角形,得到∠RPQ=∠R=60°,
∴∠PMN=90°,且PB=BC﹣CP=6﹣t,∠RNM=30°,
∴PM=(6﹣t),故MR=PR﹣PM=(t+1)﹣(6﹣t)=(3t﹣4),
∴MN=MR?tan60°=(3t﹣4),
则重叠部分的面积y=(t+1)2﹣(3t﹣4)2
=﹣t2+t﹣
=﹣(t﹣2)2+;(8分)
当≤t<6时,如图3:同理可得y=(6﹣t)2;(11分)
当t≥6时,如图4:可得y=0.(12分)
10.解:(1)△ABF∽△GBC,△FDE∽△CGE∽△BCE.
(2)∵BE平分∠B,
∴∠ABE=∠EBC,
∵AD∥BC,
∴∠AFB=∠EBC,
∴∠ABE=∠AFB,
∴AB=AF.
∴AF=4,DF=1.
∵AD∥BC,
∴DF:BC=DE:EC,
∴DE=,CE=.
∵AD∥BC,AB=CD,
∴∠BCD=∠ABC.
∵CG平分∠BCD,BE平分∠ABC,
∴∠CBG=∠BCG,
∴BG=CG.
设BG=CG=x,则由△FDE∽△CGE,得
DF:CG=DE:GE,
∴GE=x.
又由△CGE∽△BCE,得
EC2=EG?EB,
即=x?(x+x),
∴x=,
即BG=.
(3)①连接AP,当BP=AP时,点A在圆P上,此时△ABP∽△ABF,求得BP=,
即BP>AP时,点A在⊙P内.
∴当<BP≤时,点A在⊙P内.
②根据①求得BE=,
∴BP<BE,即BP<时,点A在⊙P内而点E在⊙P外
∴当<BP<时,点A在⊙P内而点E在⊙P外.
