2020-2021学年苏科版数学八年级下册第九章《中心对称图形—平行四边形》易错题专练(五)(Word版 含解析)
文档属性
| 名称 | 2020-2021学年苏科版数学八年级下册第九章《中心对称图形—平行四边形》易错题专练(五)(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 176.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-21 22:34:37 | ||
图片预览

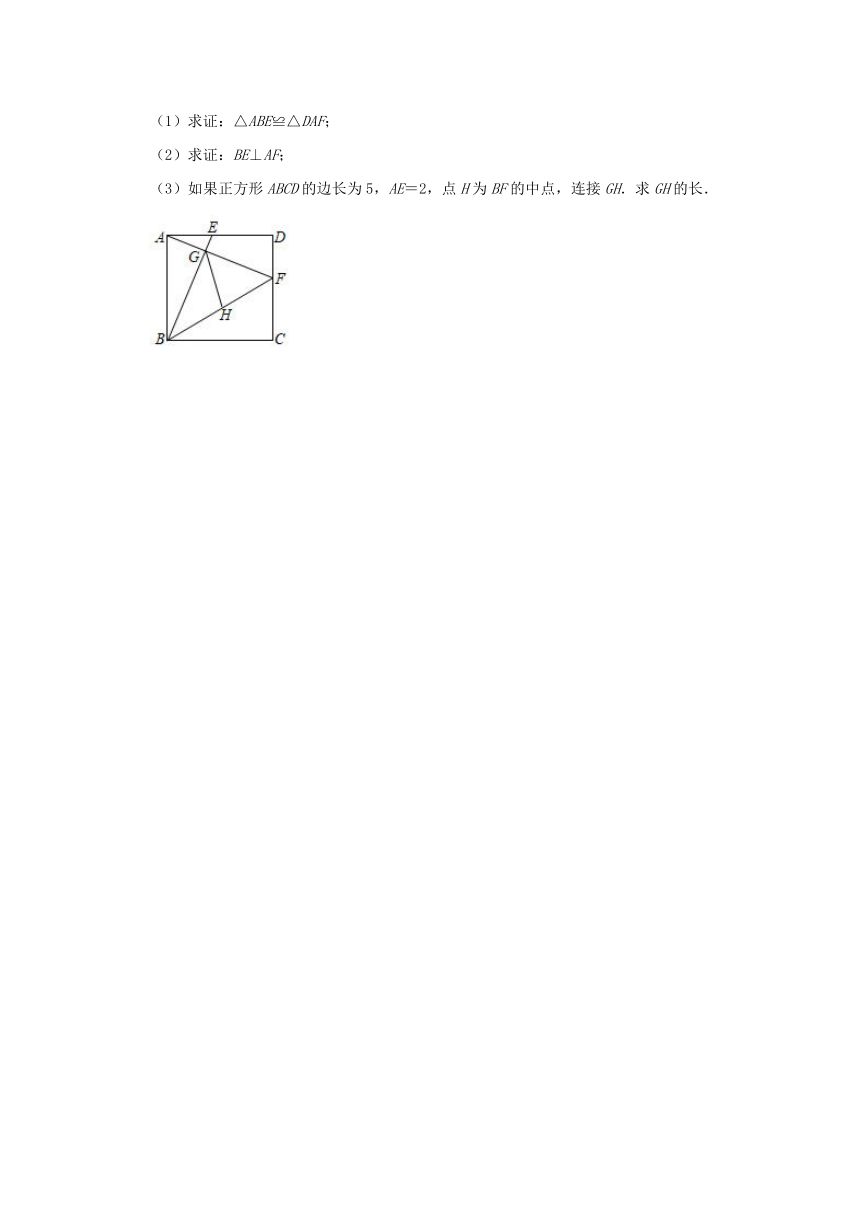
文档简介
八年级下册第九章《中心对称图形—平行四边形》
易错题专练(五)
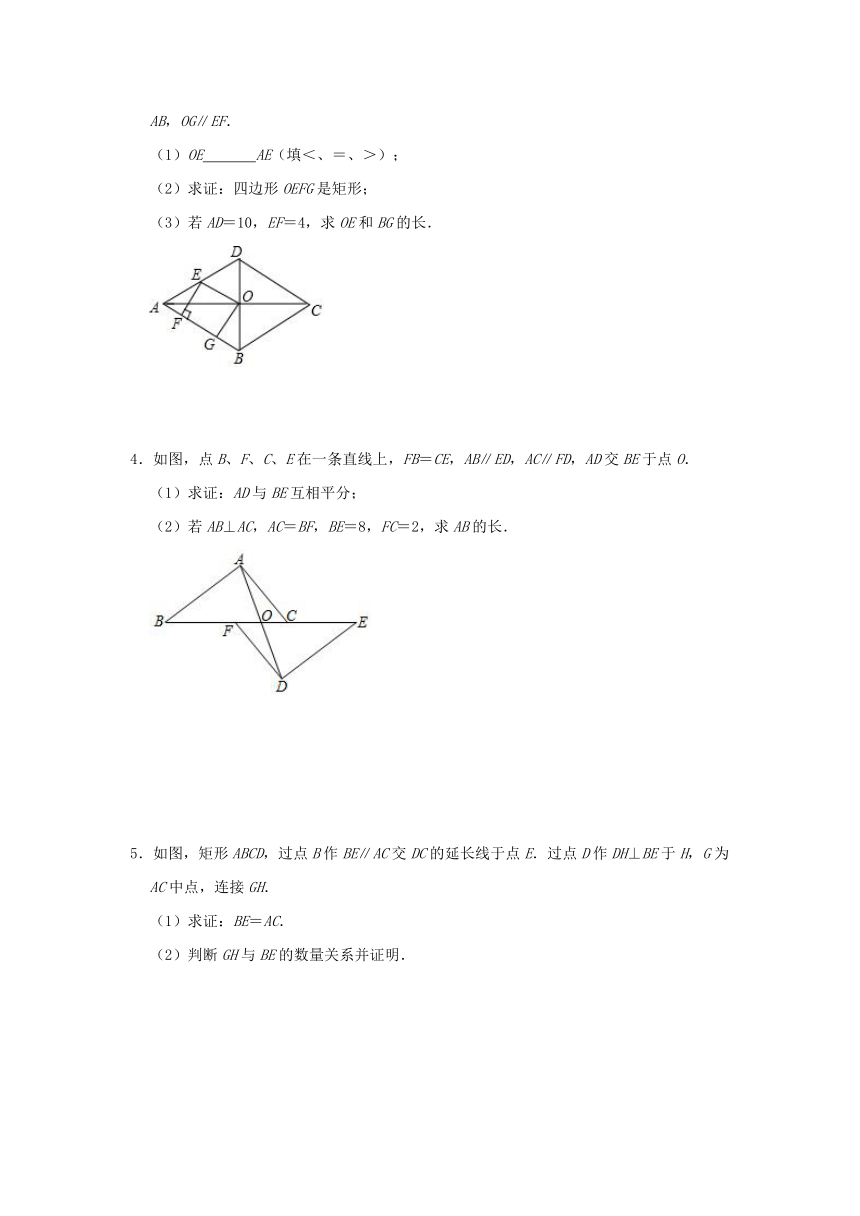
1.已知O为直线AB上的一点,∠COE是直角,OF平分∠AOE.
(1)如图1,若∠COF=34°,则∠BOE= ;若∠COF=n°,则∠BOE= ;∠BOE与∠COF的数量关系为 .
(2)当射线OE绕点O逆时针旋转到如图2的位置时,(1)中∠BOE与∠COF的数量关系是否仍然成立?如成立请写出关系式;如不成立请说明理由.
(3)在图3中,若∠COF=65°,在∠BOE的内部是否存在一条射线OD,使得2∠BOD与∠AOF的和等于∠BOE与∠BOD的差的一半?若存在,请求出∠BOD的度数;若不存在,请说明理由.
2.如图1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上.
(1)当△ABC绕点A逆时针旋转α(0°<α<90°)时,如图2,求证:BD=CF;
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长DB交CF于点H.连接BF、DF,延长AB交DF与M,连接HM.找出所有与∠MHB和为45度的角.
3.如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF.
(1)OE AE(填<、=、>);
(2)求证:四边形OEFG是矩形;
(3)若AD=10,EF=4,求OE和BG的长.
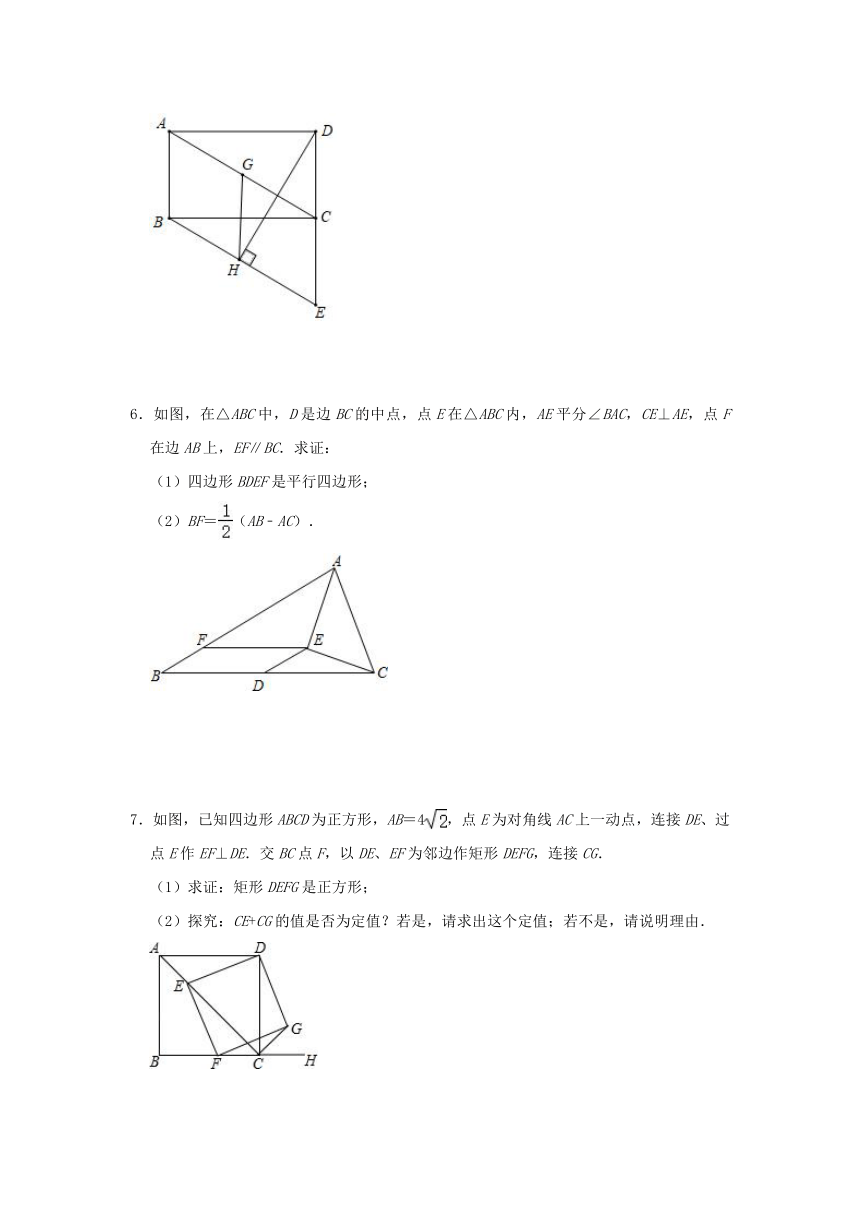
4.如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD,AD交BE于点O.
(1)求证:AD与BE互相平分;
(2)若AB⊥AC,AC=BF,BE=8,FC=2,求AB的长.
5.如图,矩形ABCD,过点B作BE∥AC交DC的延长线于点E.过点D作DH⊥BE于H,G为AC中点,连接GH.
(1)求证:BE=AC.
(2)判断GH与BE的数量关系并证明.
6.如图,在△ABC中,D是边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在边AB上,EF∥BC.求证:
(1)四边形BDEF是平行四边形;
(2)BF=(AB﹣AC).
7.如图,已知四边形ABCD为正方形,AB=4,点E为对角线AC上一动点,连接DE、过点E作EF⊥DE.交BC点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
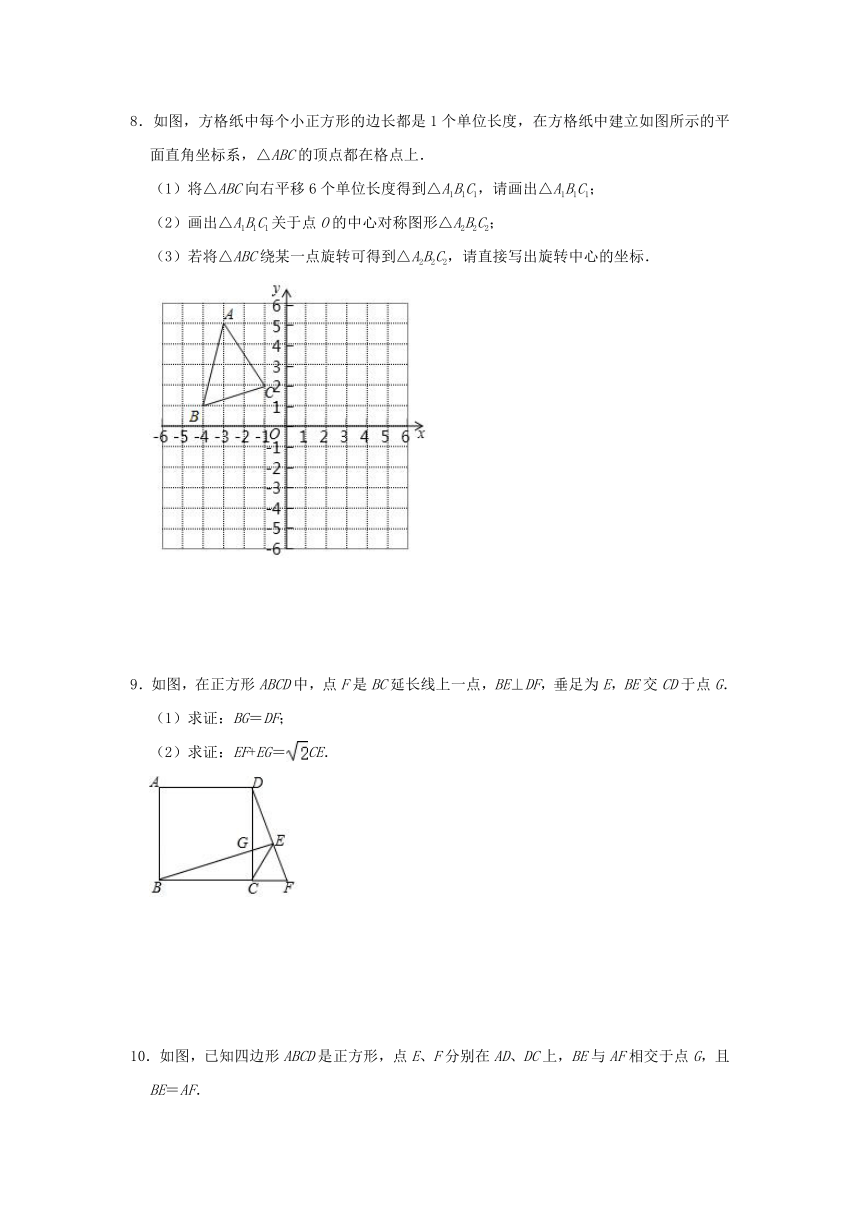
8.如图,方格纸中每个小正方形的边长都是1个单位长度,在方格纸中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上.
(1)将△ABC向右平移6个单位长度得到△A1B1C1,请画出△A1B1C1;
(2)画出△A1B1C1关于点O的中心对称图形△A2B2C2;
(3)若将△ABC绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.
9.如图,在正方形ABCD中,点F是BC延长线上一点,BE⊥DF,垂足为E,BE交CD于点G.
(1)求证:BG=DF;
(2)求证:EF+EG=CE.
10.如图,已知四边形ABCD是正方形,点E、F分别在AD、DC上,BE与AF相交于点G,且BE=AF.
(1)求证:△ABE≌△DAF;
(2)求证:BE⊥AF;
(3)如果正方形ABCD的边长为5,AE=2,点H为BF的中点,连接GH.求GH的长.
参考答案
1.解:(1)∵∠COE是直角,∠COF=34°,
∴∠EOF=90°﹣34°=56°,
由∵OF平分∠AOE.
∴∠AOE=2∠EOF=112°,
∴∠BOE=180°﹣112°=68°;
当∠COF=n°,
∴∠EOF=90°﹣n°,
∴∠AOE=2∠EOF=180°﹣2n°,
∴∠BOE=180°﹣(180°﹣2n°)=2n°,
所以有∠BOE=2∠COF.
故答案为:68°,2n°,∠BOE=2∠COF;
(2)∠BOE与∠COF的数量关系仍然成立.理由如下:
设∠COF=n°,如图2,
∵∠COE是直角,
∴∠EOF=90°﹣n°,
又∵OF平分∠AOE.
∴∠AOE=2∠EOF=180°﹣2n°,
∴∠BOE=180°﹣(180°﹣2n°)=2n°,
即∠BOE=2∠COF;
(3)存在.理由如下:
如图3,∵∠COF=65°,
∴∠BOE=2×65°=130°,
∠EOF=∠AOF=90°﹣65°=25°,
而2∠BOD与∠AOF的和等于∠BOE与∠BOD的差的一半,
∴2∠BOD+25°=(130°﹣∠BOD),
∴∠BOD=16°.
2.(l)证明:如图2中,
由旋转得:AC=AB,∠CAF=∠BAD=α;AF=AD,
在△ABD和△ACF中,
,
∴△ABD≌△ACF(SAS),
∴BD=CF.
(2)解:如图3中,设AF交DH于J.
∵△ABD≌△ACF,
∴∠AFC=∠ADB,
∵∠FJH=∠AJD,
∴∠FHJ=∠DAJ=90°,
∵∠BAD=∠BAF=45°,AF=AD,
∴AM⊥DF,NF=MD,
∴BF=BD,
∴∠BFM=∠BDM,
∴∠BMF=∠BHF=90°,
∴B,M,F,H四点共圆,
∴∠MHB=∠BFM,
∵∠AFB+∠DFB=45°,∠ADB+∠BDF=45°,
∴与∠MHB和为45度的角有∠AFB,∠ADB,∠AFC.
3.(1)解:∵四边形ABCD是菱形,
∴AC⊥BD,
∵E是AD的中点,
∴OE=AD=AE,
故答案为:=;
(2)证明:∵四边形ABCD是菱形,
∴OB=OD,
∵E是AD的中点,
∴OE是△ABD的中位线,
∴OE∥FG,
∵OG∥EF,
∴四边形OEFG是平行四边形,
∵EF⊥AB,
∴∠EFG=90°,
∴平行四边形OEFG是矩形;
(3)解:∵四边形ABCD是菱形,
∴BD⊥AC,AB=AD=10,
∴∠AOD=90°,
∵E是AD的中点,
∴OE=AE=AD=5;
由(1)知,四边形OEFG是矩形,
∴FG=OE=5,
∵AE=5,EF=4,
∴AF===3,
∴BG=AB﹣AF﹣FG=10﹣3﹣5=2.
4.(1)证明:如图,连接BD、AE,
∵FB=CE,
∴BC=EF,
又∵AB∥ED,AC∥FD,
∴∠ABC=∠DEF,∠ACB=∠DFE,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA),
∴AB=DE,
又∵AB∥DE,
∴四边形ABDE是平行四边形,
∴AD与BE互相平分;
(2)解:∵FB=CE,
∴BE=2BF+FC,
∴BF===3,
∴AC=BF=3,BC=BF+FC=3+2=5,
∵AB⊥AC,
∴由勾股定理得:AB===4.
5.(1)证明:∵四边形ABCD是矩形,
∴AB∥CD,
∵AC∥BE,
∴四边形ABEC是平行四边形,
∴BE=AC;
(2)GH=BE,
证明:连接BD,
∵四边形ABCD是矩形,G为AC的中点,
∴G为BD的中点,AC=BD,
∵DH⊥BE,即∠DHB=90°,
∴GH=BD,
∵AC=BD,AC═BE,
∴GH=BE.
6.证明:(1)延长CE交AB于点G,如图所示:
∵AE⊥CE,
∴∠AEG=∠AEC=90°,
在△AEG和△AEC中,
,
∴△AGE≌△ACE(ASA),
∴GE=EC,
∵D是边BC的中点,
∴DE为△CGB的中位线,
∴DE∥AB.
∵EF∥BC,
∴四边形BDEF是平行四边形.
(2)由(1)可知,四边形BDEF是平行四边形,
∴BF=DE.
∵D、E分别是BC、GC的中点,
∴BF=DE=BG.
∵△AGE≌△ACE,
∴AG=AC,
∴BF=(AB﹣AG)=(AB﹣AC).
7.解:(1)如图所示,过E作EM⊥BC于M点,过E作EN⊥CD于N点,
∵正方形ABCD,
∴∠BCD=90°,∠ECN=45°,
∴∠EMC=∠ENC=∠BCD=90°,且NE=NC,
∴四边形EMCN为正方形,
∵四边形DEFG是矩形,
∴EM=EN,∠DEN+∠NEF=∠MEF+∠NEF=90°,
∴∠DEN=∠MEF,
又∠DNE=∠FME=90°,
在△DEN和△FEM中,,
∴△DEN≌△FEM(ASA),
∴ED=EF,
∴矩形DEFG为正方形,
(2)CE+CG的值为定值,理由如下:
∵矩形DEFG为正方形,
∴DE=DG,∠EDC+∠CDG=90°,
∵四边形ABCD是正方形,
∵AD=DC,∠ADE+∠EDC=90°,
∴∠ADE=∠CDG,
在△ADE和△CDG中,,
∴△ADE≌△CDG(SAS),
∴AE=CG,
∴AC=AE+CE=AB=×4=8,
∴CE+CG=8是定值.
8.解:(1)如图,△A1B1C1即为所求;
(2)如图,△A2B2C2即为所求;
(3)根据图形可知:
旋转中心的坐标为:(﹣3,0).
9.解:(1)证明:
∵四边形ABCD是正方形,
∴∠BCG=∠DCB=∠DCF=90°,BC=DC,
∵BE⊥DF,
∴∠CBG+∠F=∠CDF+∠F,
∴∠CBG=∠CDF,
在△CBG和△CDF中,
,
∴△CBG≌△CDF(ASA),
∴BG=DF;
(2)如图,过点C作CM⊥CE交BE于点M,
∵△CBG≌△CDF,
∴CG=CF,∠F=∠CGB,
∵∠MCG+∠DCE=∠ECF+∠DCE=90°,
∴∠MCG=∠ECF,
在△MCG和△ECF中,
,
∴△MCG≌△ECF(ASA),
∴MG=EF,CM=CE,
∴△CME是等腰直角三角形,
∴ME=CE,
又∵ME=MG+EG=EF+EG,
∴EF+EG=CE.
10.解:(1)证明:∵四边形ABCD为正方形,
∴∠BAE=∠D=90°,AB=AD,
在Rt△ABE和Rt△DAF中,
,
∴Rt△ABE≌Rt△DAF(HL);
(2)证明:∵Rt△ABE≌Rt△DAF,
∴∠ABE=∠DAF,
∵∠ABE+∠BEA=90°,
∴∠DAF+∠BEA=90°,
∴∠AGE=∠BGF=90°,
∴BE⊥AF;
(3)∵BE⊥AF,
∵点H为BF的中点,
∴GH=BF,
∵在Rt△BCF中,BC=5,CF=CD﹣DF=5﹣2=3,根据勾股定理,得
∴BF==,
∴GH=.
易错题专练(五)
1.已知O为直线AB上的一点,∠COE是直角,OF平分∠AOE.
(1)如图1,若∠COF=34°,则∠BOE= ;若∠COF=n°,则∠BOE= ;∠BOE与∠COF的数量关系为 .
(2)当射线OE绕点O逆时针旋转到如图2的位置时,(1)中∠BOE与∠COF的数量关系是否仍然成立?如成立请写出关系式;如不成立请说明理由.
(3)在图3中,若∠COF=65°,在∠BOE的内部是否存在一条射线OD,使得2∠BOD与∠AOF的和等于∠BOE与∠BOD的差的一半?若存在,请求出∠BOD的度数;若不存在,请说明理由.
2.如图1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上.
(1)当△ABC绕点A逆时针旋转α(0°<α<90°)时,如图2,求证:BD=CF;
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长DB交CF于点H.连接BF、DF,延长AB交DF与M,连接HM.找出所有与∠MHB和为45度的角.
3.如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF.
(1)OE AE(填<、=、>);
(2)求证:四边形OEFG是矩形;
(3)若AD=10,EF=4,求OE和BG的长.
4.如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD,AD交BE于点O.
(1)求证:AD与BE互相平分;
(2)若AB⊥AC,AC=BF,BE=8,FC=2,求AB的长.
5.如图,矩形ABCD,过点B作BE∥AC交DC的延长线于点E.过点D作DH⊥BE于H,G为AC中点,连接GH.
(1)求证:BE=AC.
(2)判断GH与BE的数量关系并证明.
6.如图,在△ABC中,D是边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在边AB上,EF∥BC.求证:
(1)四边形BDEF是平行四边形;
(2)BF=(AB﹣AC).
7.如图,已知四边形ABCD为正方形,AB=4,点E为对角线AC上一动点,连接DE、过点E作EF⊥DE.交BC点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
8.如图,方格纸中每个小正方形的边长都是1个单位长度,在方格纸中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上.
(1)将△ABC向右平移6个单位长度得到△A1B1C1,请画出△A1B1C1;
(2)画出△A1B1C1关于点O的中心对称图形△A2B2C2;
(3)若将△ABC绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.
9.如图,在正方形ABCD中,点F是BC延长线上一点,BE⊥DF,垂足为E,BE交CD于点G.
(1)求证:BG=DF;
(2)求证:EF+EG=CE.
10.如图,已知四边形ABCD是正方形,点E、F分别在AD、DC上,BE与AF相交于点G,且BE=AF.
(1)求证:△ABE≌△DAF;
(2)求证:BE⊥AF;
(3)如果正方形ABCD的边长为5,AE=2,点H为BF的中点,连接GH.求GH的长.
参考答案
1.解:(1)∵∠COE是直角,∠COF=34°,
∴∠EOF=90°﹣34°=56°,
由∵OF平分∠AOE.
∴∠AOE=2∠EOF=112°,
∴∠BOE=180°﹣112°=68°;
当∠COF=n°,
∴∠EOF=90°﹣n°,
∴∠AOE=2∠EOF=180°﹣2n°,
∴∠BOE=180°﹣(180°﹣2n°)=2n°,
所以有∠BOE=2∠COF.
故答案为:68°,2n°,∠BOE=2∠COF;
(2)∠BOE与∠COF的数量关系仍然成立.理由如下:
设∠COF=n°,如图2,
∵∠COE是直角,
∴∠EOF=90°﹣n°,
又∵OF平分∠AOE.
∴∠AOE=2∠EOF=180°﹣2n°,
∴∠BOE=180°﹣(180°﹣2n°)=2n°,
即∠BOE=2∠COF;
(3)存在.理由如下:
如图3,∵∠COF=65°,
∴∠BOE=2×65°=130°,
∠EOF=∠AOF=90°﹣65°=25°,
而2∠BOD与∠AOF的和等于∠BOE与∠BOD的差的一半,
∴2∠BOD+25°=(130°﹣∠BOD),
∴∠BOD=16°.
2.(l)证明:如图2中,
由旋转得:AC=AB,∠CAF=∠BAD=α;AF=AD,
在△ABD和△ACF中,
,
∴△ABD≌△ACF(SAS),
∴BD=CF.
(2)解:如图3中,设AF交DH于J.
∵△ABD≌△ACF,
∴∠AFC=∠ADB,
∵∠FJH=∠AJD,
∴∠FHJ=∠DAJ=90°,
∵∠BAD=∠BAF=45°,AF=AD,
∴AM⊥DF,NF=MD,
∴BF=BD,
∴∠BFM=∠BDM,
∴∠BMF=∠BHF=90°,
∴B,M,F,H四点共圆,
∴∠MHB=∠BFM,
∵∠AFB+∠DFB=45°,∠ADB+∠BDF=45°,
∴与∠MHB和为45度的角有∠AFB,∠ADB,∠AFC.
3.(1)解:∵四边形ABCD是菱形,
∴AC⊥BD,
∵E是AD的中点,
∴OE=AD=AE,
故答案为:=;
(2)证明:∵四边形ABCD是菱形,
∴OB=OD,
∵E是AD的中点,
∴OE是△ABD的中位线,
∴OE∥FG,
∵OG∥EF,
∴四边形OEFG是平行四边形,
∵EF⊥AB,
∴∠EFG=90°,
∴平行四边形OEFG是矩形;
(3)解:∵四边形ABCD是菱形,
∴BD⊥AC,AB=AD=10,
∴∠AOD=90°,
∵E是AD的中点,
∴OE=AE=AD=5;
由(1)知,四边形OEFG是矩形,
∴FG=OE=5,
∵AE=5,EF=4,
∴AF===3,
∴BG=AB﹣AF﹣FG=10﹣3﹣5=2.
4.(1)证明:如图,连接BD、AE,
∵FB=CE,
∴BC=EF,
又∵AB∥ED,AC∥FD,
∴∠ABC=∠DEF,∠ACB=∠DFE,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA),
∴AB=DE,
又∵AB∥DE,
∴四边形ABDE是平行四边形,
∴AD与BE互相平分;
(2)解:∵FB=CE,
∴BE=2BF+FC,
∴BF===3,
∴AC=BF=3,BC=BF+FC=3+2=5,
∵AB⊥AC,
∴由勾股定理得:AB===4.
5.(1)证明:∵四边形ABCD是矩形,
∴AB∥CD,
∵AC∥BE,
∴四边形ABEC是平行四边形,
∴BE=AC;
(2)GH=BE,
证明:连接BD,
∵四边形ABCD是矩形,G为AC的中点,
∴G为BD的中点,AC=BD,
∵DH⊥BE,即∠DHB=90°,
∴GH=BD,
∵AC=BD,AC═BE,
∴GH=BE.
6.证明:(1)延长CE交AB于点G,如图所示:
∵AE⊥CE,
∴∠AEG=∠AEC=90°,
在△AEG和△AEC中,
,
∴△AGE≌△ACE(ASA),
∴GE=EC,
∵D是边BC的中点,
∴DE为△CGB的中位线,
∴DE∥AB.
∵EF∥BC,
∴四边形BDEF是平行四边形.
(2)由(1)可知,四边形BDEF是平行四边形,
∴BF=DE.
∵D、E分别是BC、GC的中点,
∴BF=DE=BG.
∵△AGE≌△ACE,
∴AG=AC,
∴BF=(AB﹣AG)=(AB﹣AC).
7.解:(1)如图所示,过E作EM⊥BC于M点,过E作EN⊥CD于N点,
∵正方形ABCD,
∴∠BCD=90°,∠ECN=45°,
∴∠EMC=∠ENC=∠BCD=90°,且NE=NC,
∴四边形EMCN为正方形,
∵四边形DEFG是矩形,
∴EM=EN,∠DEN+∠NEF=∠MEF+∠NEF=90°,
∴∠DEN=∠MEF,
又∠DNE=∠FME=90°,
在△DEN和△FEM中,,
∴△DEN≌△FEM(ASA),
∴ED=EF,
∴矩形DEFG为正方形,
(2)CE+CG的值为定值,理由如下:
∵矩形DEFG为正方形,
∴DE=DG,∠EDC+∠CDG=90°,
∵四边形ABCD是正方形,
∵AD=DC,∠ADE+∠EDC=90°,
∴∠ADE=∠CDG,
在△ADE和△CDG中,,
∴△ADE≌△CDG(SAS),
∴AE=CG,
∴AC=AE+CE=AB=×4=8,
∴CE+CG=8是定值.
8.解:(1)如图,△A1B1C1即为所求;
(2)如图,△A2B2C2即为所求;
(3)根据图形可知:
旋转中心的坐标为:(﹣3,0).
9.解:(1)证明:
∵四边形ABCD是正方形,
∴∠BCG=∠DCB=∠DCF=90°,BC=DC,
∵BE⊥DF,
∴∠CBG+∠F=∠CDF+∠F,
∴∠CBG=∠CDF,
在△CBG和△CDF中,
,
∴△CBG≌△CDF(ASA),
∴BG=DF;
(2)如图,过点C作CM⊥CE交BE于点M,
∵△CBG≌△CDF,
∴CG=CF,∠F=∠CGB,
∵∠MCG+∠DCE=∠ECF+∠DCE=90°,
∴∠MCG=∠ECF,
在△MCG和△ECF中,
,
∴△MCG≌△ECF(ASA),
∴MG=EF,CM=CE,
∴△CME是等腰直角三角形,
∴ME=CE,
又∵ME=MG+EG=EF+EG,
∴EF+EG=CE.
10.解:(1)证明:∵四边形ABCD为正方形,
∴∠BAE=∠D=90°,AB=AD,
在Rt△ABE和Rt△DAF中,
,
∴Rt△ABE≌Rt△DAF(HL);
(2)证明:∵Rt△ABE≌Rt△DAF,
∴∠ABE=∠DAF,
∵∠ABE+∠BEA=90°,
∴∠DAF+∠BEA=90°,
∴∠AGE=∠BGF=90°,
∴BE⊥AF;
(3)∵BE⊥AF,
∵点H为BF的中点,
∴GH=BF,
∵在Rt△BCF中,BC=5,CF=CD﹣DF=5﹣2=3,根据勾股定理,得
∴BF==,
∴GH=.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
