2020-2021学年七年级沪教版(上海)下册数学第十三章《相交线 平行线》基础提升卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年七年级沪教版(上海)下册数学第十三章《相交线 平行线》基础提升卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 848.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-21 22:38:25 | ||
图片预览

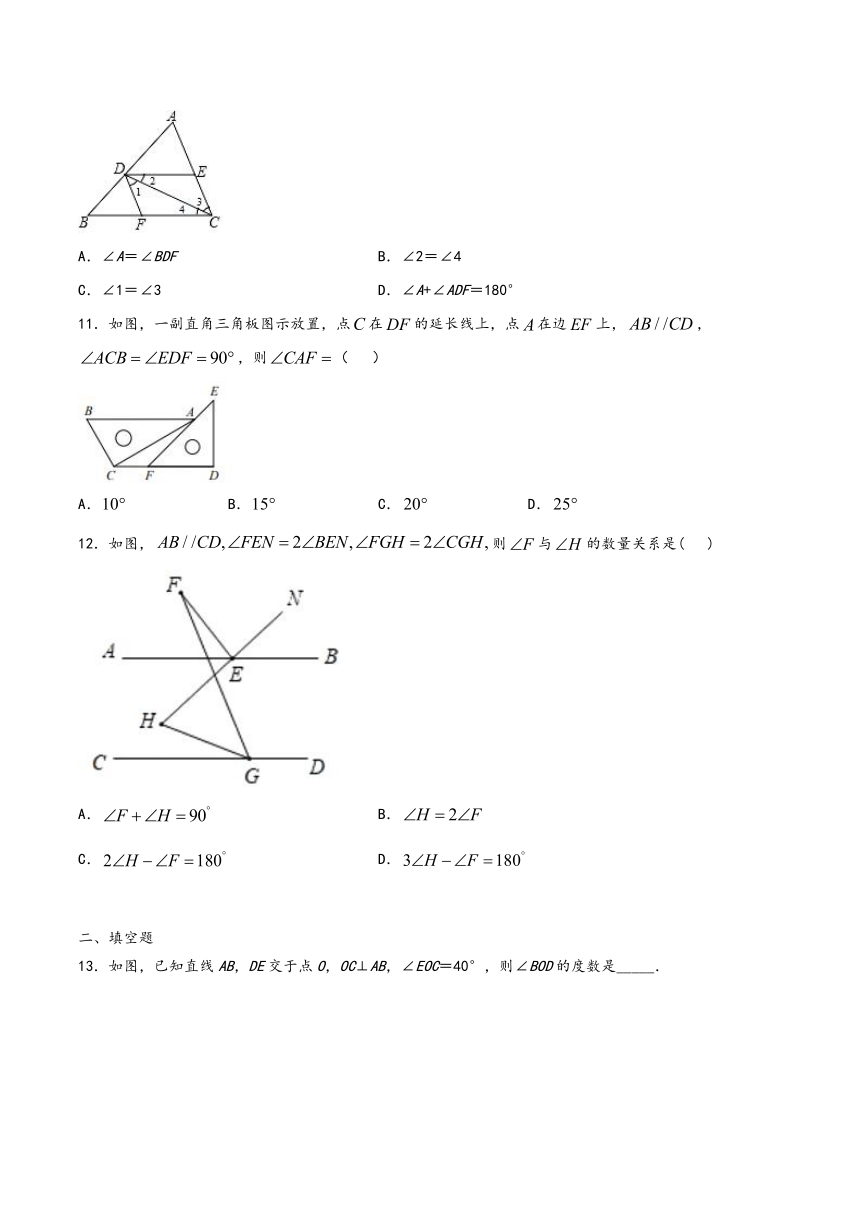
文档简介
2020-2021学年七年级沪教版(上海)下册数学第十三章《相交线 平行线》基础提升卷
一、单选题
1.下列说法错误的是( )
A.对顶角相等 B.两点之间所有连线中,线段最短
C.等角的补角相等 D.过任意一点P,只能画一条直线
2.如图,是直线外一点,从点向直线引,,,几条线段,其中只有与垂直,这几条线段中长度最短的是( )
A. B. C. D.
3.如图,和不是同位角的是( )
A. B.C. D.
4.如图,下列条件能判断的是( )
A. B. C. D.
5.如图,BE,CE分别平分∠ABC,∠ACD,EF∥BC,交AB于点F,交AC于点G,若BF=7,CG=5,则FG长为( )
A.2 B.2.5 C.3 D.3.5
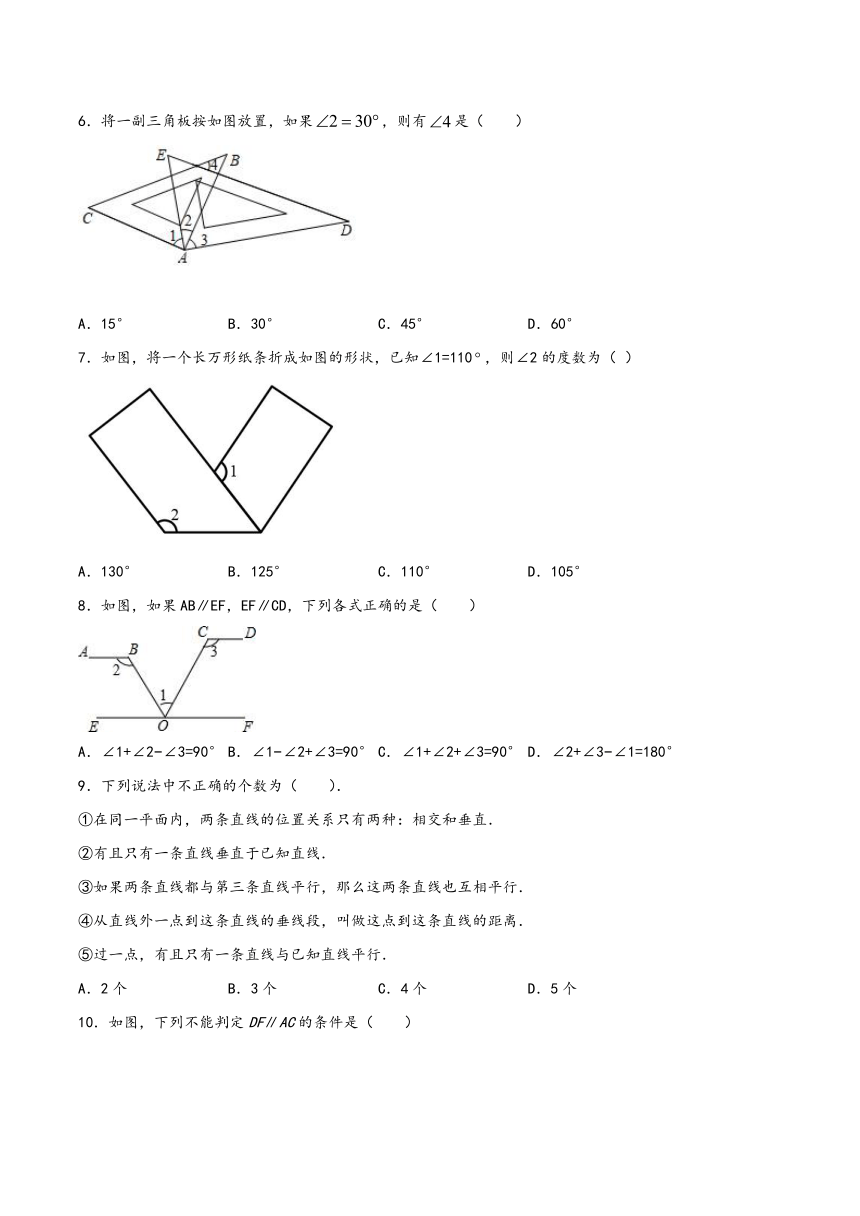
6.将一副三角板按如图放置,如果,则有是( )
A.15° B.30° C.45° D.60°
7.如图,将一个长万形纸条折成如图的形状,已知∠1=110,则∠2的度数为( )
A.130° B.125° C.110° D.105°
8.如图,如果AB∥EF,EF∥CD,下列各式正确的是( )
A.∠1+∠2?∠3=90° B.∠1?∠2+∠3=90° C.∠1+∠2+∠3=90° D.∠2+∠3?∠1=180°
9.下列说法中不正确的个数为( ).
①在同一平面内,两条直线的位置关系只有两种:相交和垂直.
②有且只有一条直线垂直于已知直线.
③如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
④从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离.
⑤过一点,有且只有一条直线与已知直线平行.
A.2个 B.3个 C.4个 D.5个
10.如图,下列不能判定DF∥AC的条件是( )
A.∠A=∠BDF B.∠2=∠4
C.∠1=∠3 D.∠A+∠ADF=180°
11.如图,一副直角三角板图示放置,点在的延长线上,点在边上,,,则( )
A. B. C. D.
12.如图,则与的数量关系是( )
A. B.
C. D.
二、填空题
13.如图,已知直线AB,DE交于点O,OC⊥AB,∠EOC=40°,则∠BOD的度数是_____.
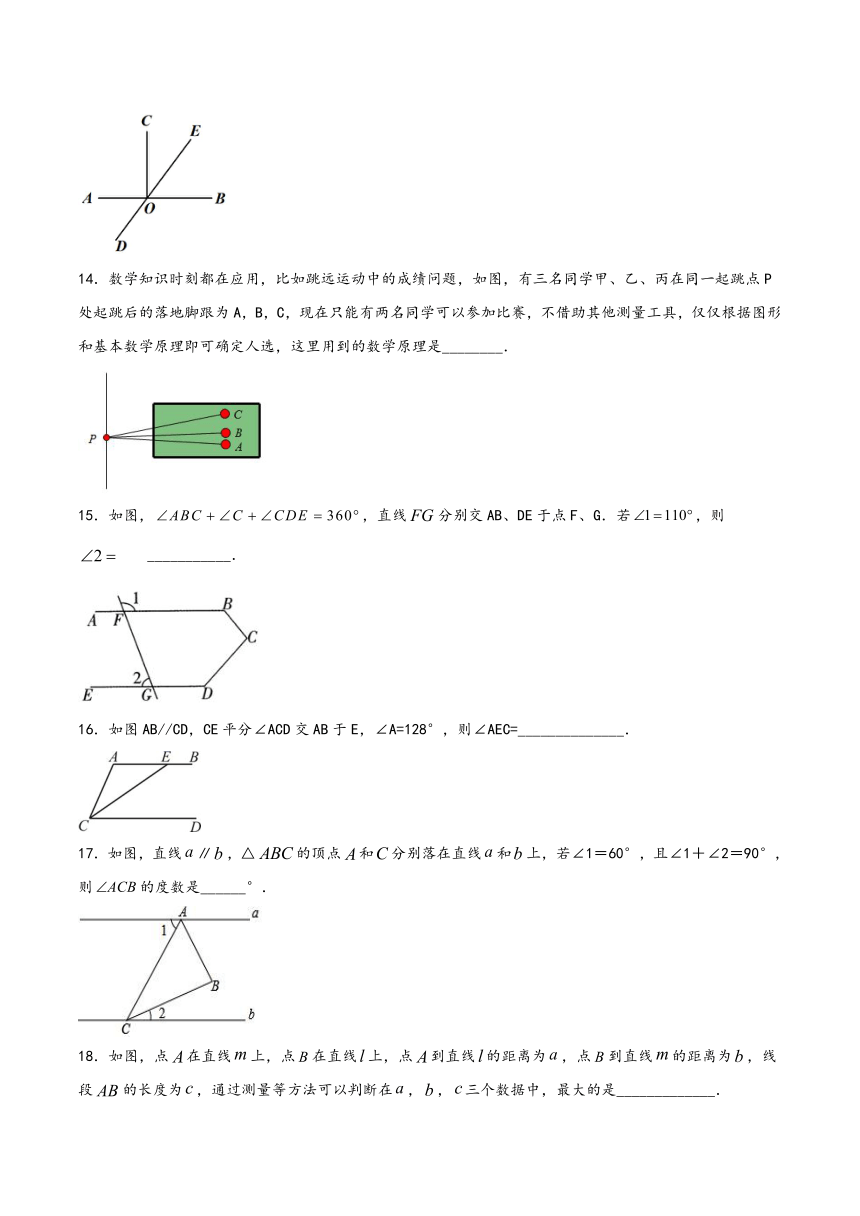
14.数学知识时刻都在应用,比如跳远运动中的成绩问题,如图,有三名同学甲、乙、丙在同一起跳点P处起跳后的落地脚跟为A,B,C,现在只能有两名同学可以参加比赛,不借助其他测量工具,仅仅根据图形和基本数学原理即可确定人选,这里用到的数学原理是________.
15.如图,,直线分别交AB、DE于点F、G.若,则___________.
16.如图AB//CD,CE平分∠ACD交AB于E,∠A=128°,则∠AEC=______________.
17.如图,直线∥,△的顶点和分别落在直线和上,若∠1=60°,且∠1+∠2=90°,则的度数是______°.
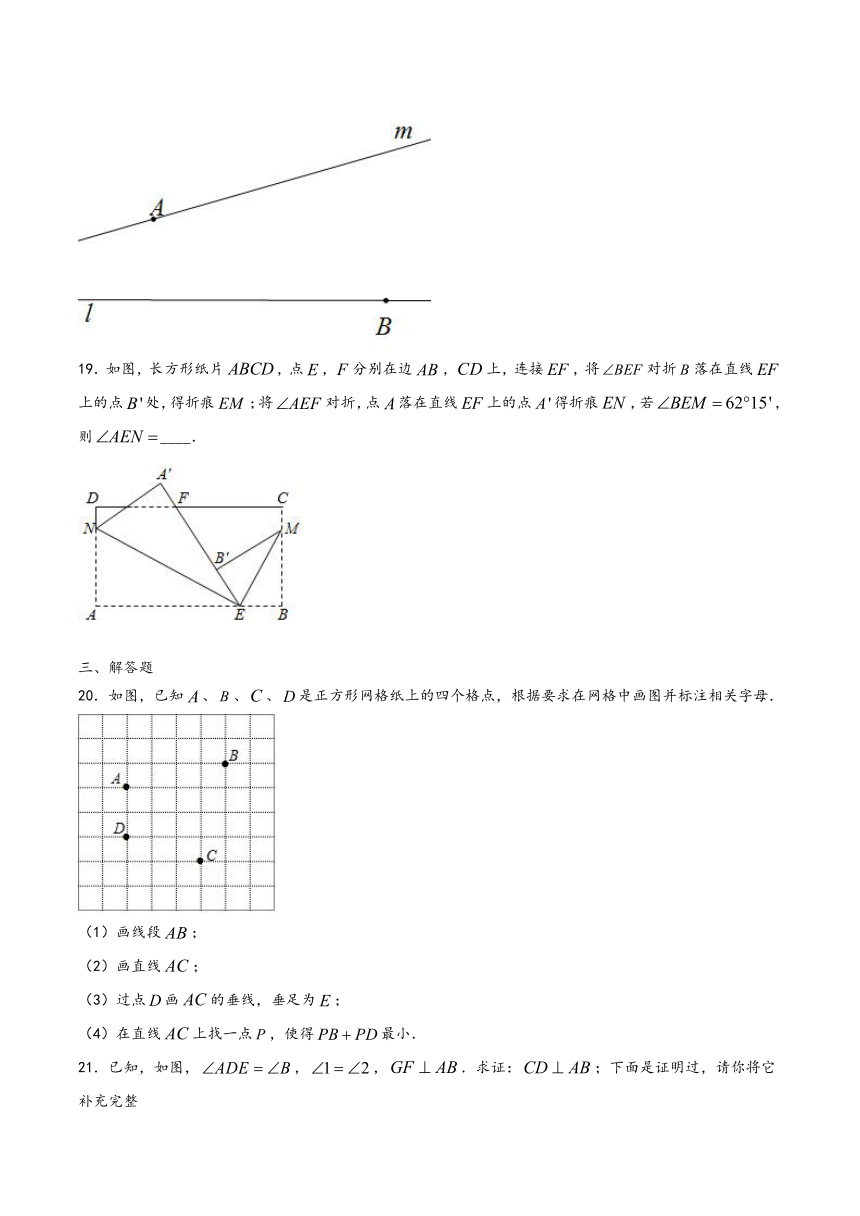
18.如图,点在直线上,点在直线上,点到直线的距离为,点到直线的距离为,线段的长度为,通过测量等方法可以判断在,,三个数据中,最大的是_____________.
19.如图,长方形纸片,点,分别在边,上,连接,将对折落在直线上的点处,得折痕;将对折,点落在直线上的点得折痕,若,则____.
三、解答题
20.如图,已知、、、是正方形网格纸上的四个格点,根据要求在网格中画图并标注相关字母.
(1)画线段;
(2)画直线;
(3)过点画的垂线,垂足为;
(4)在直线上找一点,使得最小.
21.已知,如图,,,.求证:;下面是证明过,请你将它补充完整
证明:∵
∴ ( )
∴
又∵
∴
∴ ( )
∴
∵
∴
∴
∴
22.如图,,.
(1)吗?说明理由.
(2)求的度数.
23.如图,在中,垂足为点,点在边上,垂足为点.点在边上,且.求的度数.
24.如图,已知点E在直线DC上,射线EF平分,过E点作,G为射线EC上一点,连接BG,且.
(1)求证:;
(2)若,求证:.
25.已知:△ABC和平面内一点D.
(1)如图1,点D在BC边上,过D点作DE//BA交AC于点E,作DF//CA交AB于点F,判断∠EDF与∠A的数量关系,并说明理由.
(2)如图2,点D在BC的延长线上,DF//CA,∠EDF=∠A,请你判断DE与BA的位置关系.并说明理由.
(3)如图3,点D在△ABC的外部,若作DE//BA,DF//CA,请直接写出∠EDF与∠A数量关系.
26.已知:如图1,,点,分别为,上一点.
(1)在,之间有一点(点不在线段上),连接,,探究,,之间有怎样的数量关系,请补全图形,并在图形下面写出相应的数量关系,选其中一个进行证明.
(2)如图2,在,之两点,,连接,,,请选择一个图形写出,,,存在的数量关系(不需证明).
参考答案
1.D
解:A、对顶角相等,此选项正确,不符合题意;
B、两点之间所有连线中,线段最短,此选项正确,不符合题意;
C、等角的补角相等,此选项正确,不符合题意;
D、过任意一点P,能画无数条直线,此选项错误,符合题意;
2.B
解:直线外一点 P 与直线上各点连接的所有线段中,最短的是 PB ,依据是垂线段最短.
故答案选B.
3.C
解:A、∠1和∠2是同位角,故此选项不符合题意;
B、∠1和∠2是同位角,故此选项不符合题意;
C、∠1和∠2不是同位角,故此选项符合题意;
D、∠1和∠2是同位角,故此选项不符合题意;
4.C
解:A、∠D+∠DAB=180°,则AB∥DC,故选项错误;
B、∠1=∠2,则AB∥DC,故选项错误;
C、∠3=∠4,AD∥BC,故选项正确;
D、∠4=∠5,不能判定,故选项错误;
5.A
解:∵BE,CE分别平分∠ABC,∠ACD,
∴∠FBE=∠EBC,∠ACE=∠ECD,
∵EF∥BC,
∴∠FEB=∠EBC,∠ECD=∠FEC,
∴∠FBE=∠FEB,∠ACE=∠FEC,
∴BF=EF,CG=GE,
∴FG=EF-EG=7-5=2,
6.C
解:根据题意可知:∠E=60°,∠C=45°,∠1+∠2=90°,
∵,
∴∠1=60°,
∴∠1=∠E,
∴AC∥DE,
∴∠4=∠C=45°.
7.B
∵∠1=110°,纸条的两边互相平行,
∴∠4=180°-∠1=180°-110°=70°.
根据翻折的性质,
∠3=(180°-∠4)= 55°,
同理,∠2=180°-∠3=180°- 55°=125°.
8.D
∵EF∥CD
∴∠3=∠COE
∴∠3?∠1=∠COE?∠1=∠BOE
∵AB∥EF
∴∠2+∠BOE=180°,即∠2+∠3?∠1=180°
9.C
∵在同一平面内,两条直线的位置关系只有两种:相交和平行,故①不正确;
∵过直线外一点有且只有一条直线垂直于已知直线.故②不正确;
如果两条直线都与第三条直线平行,那么这两条直线也互相平行.故③正确;
从直线外一点到这条直线的垂线段的长度,叫做这点到这条直线的距离.故④不正确;
过直线外一点,有且只有一条直线与已知直线平行.故⑤不正确;
∴不正确的有①②④⑤四个.
10.B
解:A.∠A=∠BDF,由同位角相等,两直线平行,可判断DF∥AC;
B.∠2=∠4,不能判断DF∥AC;
C.∠1=∠3由内错角相等,两直线平行,可判断DF∥AC;
D.∠A+∠ADF=180°,由同旁内角互补,两直线平行,可判断DF∥AC;
11.B
解:∵
∴,
∵
∴
∴
12.D
设
则
∵
∴
∴
13.130°
解:∵OC⊥AB,
∴∠COB=90°.
∵∠EOC=40°,
∴∠BOE=∠COB?∠EOC=90°?40°=50°.
∴∠BOD=180°?∠BOE=180°?50°=130°.
14.垂线段最短
解:由题意可得,B同学跳远距离最近,所以可以确定A和C同学参加比赛,这里用到的数学原理是垂线段最短
15.70°.
解:如图,作CH∥AB,
∵AB∥CH,
∴∠B+∠BCH=180°,
∵∠ABC+∠BCD+∠CDE=360°,
∴∠D+∠DCH=180°,
∴CH∥DE,
∴AB∥DE,
∴∠1=∠3=110°,
∴∠2=180°-∠3=70°
16.26o
解:∵ABCD,
∴∠AEC=∠DCE,∠A+∠ACD=180°,
∴∠ACD=180°﹣∠A=180°﹣128°=52°,
∵CE平分∠ACD,
∴∠ACE=∠DCE==26°,
∴∠AEC=∠DCE=26°;
17.30
解:∵直线a∥b,
∴∠1=∠ACB+∠2=60°,
∵∠1=60°且∠1+∠2=90°
∴∠2=90°-60°=30°
∴∠ACB=60°-30°=30°,
18.
过点A作AD垂直于垂足为D,过点B作BH垂直于垂足为H,连接AB,
由题意得:AD=a, BH=b,AB=c;
根据点到直线垂线段最短,可知AB>AD,AB>BH
∴c>a,c>b;
∴c最大
19.
解:根据折叠可知:EM平分∠BEB′,
∴∠B′EM=∠BEM=62°15′,
∴∠AEA′=180°-2×62°15′=55°30′,
EN平分∠AEA′,
∴∠AEN=∠A′EN=∠AEA′=×55°30′=27°45′,
故答案为:27°45′.
20.
解:如图
21
证明:∵
∴(同位角相等,两直线平行)
∴(两直线平行 ,内错角相等)
又∵
∴
∴(同位角相等,两直线平行)
∴
∵
∴
∴
∴
22.
解:
(1).理由如下:
∵(已知),
∴(两直线平行,同位角相等)
(两直线平行,错角相等)
∵(已知),
∴(等量代换)
(2)∵(已知),
∴(平角的定义),
∵(已证),
∴(等量代换),
即.
23.110°
解:∵CD⊥AB,EF⊥AB
,
,
又,
,
,
又
24.
(1)∵,
∴,
∴.
又∵,
∴.
(2)∵平分,
∴.
∵,,
∴.
又∵,
∴,
∴.
25.
解:(1)∠EDF=∠A.
理由:∵DE∥BA,DF∥CA,
∴∠A=∠DEC,∠DEC=∠EDF,
∴∠A=∠EDF;
(2)DE∥BA.
证明:如图,延长BA交DF于G.
∵DF∥CA,
∴∠2=∠3.
又∵∠1=∠2,
∴∠1=∠3.
∴DE∥BA.
(3)∠EDF=∠A,∠EDF+∠A=180°.
理由:①如图,∵DE∥BA,DF∥CA,
∴∠D+∠E=180°,∠E+∠EAF=180°,
∴∠EDF=∠EAF=∠BAC;
②如图,∵DE∥BA,DF∥CA,
∴∠D+∠F=180°,∠F=∠CAB,
∴∠EDF+∠BAC=180°.
综上,∠EDF与∠A相等或互补
26.
解:(1)∠EMF=∠AEM+∠MFC.∠AEM+∠EMF+∠MFC=360°.
证明:过点M作MP∥AB.
∵AB∥CD,
∴MP∥CD.
∴∠4=∠3.
∵MP∥AB,
∴∠1=∠2.
∵∠EMF=∠2+∠3,
∴∠EMF=∠1+∠4.
∴∠EMF=∠AEM+∠MFC;
证明:过点M作MQ∥AB.
∵AB∥CD,
∴MQ∥CD.
∴∠CFM+∠1=180°;
∵MQ∥AB,
∴∠AEM+∠2=180°.
∴∠CFM+∠1+∠AEM+∠2=360°.
∵∠EMF=∠1+∠2,
∴∠AEM+∠EMF+∠MFC=360°;
(2)如图2第一个图:∠EMN+∠MNF-∠AEM-∠NFC=180°;
过点M作MP∥AB,过点N作NQ∥AB,
∴∠AEM=∠1,∠CFN=∠4,MP∥NQ,
∴∠2+∠3=180°,
∵∠EMN=∠1+∠2,∠MNF=∠3+∠4,
∴∠EMN+∠MNF=∠1+∠2+∠3+∠4,∠AEM+∠CFN=∠1+∠4,
∴∠EMN+∠MNF-∠AEM-∠NFC
=∠1+∠2+∠3+∠4-∠1-∠4
=∠2+∠3
=180°;
如图2第二个图:∠EMN-∠MNF+∠AEM+∠NFC=180°.
过点M作MP∥AB,过点N作NQ∥AB,
∴∠AEM+∠1=180°,∠CFN=∠4,MP∥NQ,
∴∠2=∠3,
∵∠EMN=∠1+∠2,∠MNF=∠3+∠4,
∴∠EMN-∠MNF=∠1+∠2-∠3-∠4,∠AEM+∠CFN=180°-∠1+∠4,
∴∠EMN-∠MNF+∠AEM+∠NFC
=∠1+∠2-∠3-∠4+180°-∠1+∠4
=180°.
一、单选题
1.下列说法错误的是( )
A.对顶角相等 B.两点之间所有连线中,线段最短
C.等角的补角相等 D.过任意一点P,只能画一条直线
2.如图,是直线外一点,从点向直线引,,,几条线段,其中只有与垂直,这几条线段中长度最短的是( )
A. B. C. D.
3.如图,和不是同位角的是( )
A. B.C. D.
4.如图,下列条件能判断的是( )
A. B. C. D.
5.如图,BE,CE分别平分∠ABC,∠ACD,EF∥BC,交AB于点F,交AC于点G,若BF=7,CG=5,则FG长为( )
A.2 B.2.5 C.3 D.3.5
6.将一副三角板按如图放置,如果,则有是( )
A.15° B.30° C.45° D.60°
7.如图,将一个长万形纸条折成如图的形状,已知∠1=110,则∠2的度数为( )
A.130° B.125° C.110° D.105°
8.如图,如果AB∥EF,EF∥CD,下列各式正确的是( )
A.∠1+∠2?∠3=90° B.∠1?∠2+∠3=90° C.∠1+∠2+∠3=90° D.∠2+∠3?∠1=180°
9.下列说法中不正确的个数为( ).
①在同一平面内,两条直线的位置关系只有两种:相交和垂直.
②有且只有一条直线垂直于已知直线.
③如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
④从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离.
⑤过一点,有且只有一条直线与已知直线平行.
A.2个 B.3个 C.4个 D.5个
10.如图,下列不能判定DF∥AC的条件是( )
A.∠A=∠BDF B.∠2=∠4
C.∠1=∠3 D.∠A+∠ADF=180°
11.如图,一副直角三角板图示放置,点在的延长线上,点在边上,,,则( )
A. B. C. D.
12.如图,则与的数量关系是( )
A. B.
C. D.
二、填空题
13.如图,已知直线AB,DE交于点O,OC⊥AB,∠EOC=40°,则∠BOD的度数是_____.
14.数学知识时刻都在应用,比如跳远运动中的成绩问题,如图,有三名同学甲、乙、丙在同一起跳点P处起跳后的落地脚跟为A,B,C,现在只能有两名同学可以参加比赛,不借助其他测量工具,仅仅根据图形和基本数学原理即可确定人选,这里用到的数学原理是________.
15.如图,,直线分别交AB、DE于点F、G.若,则___________.
16.如图AB//CD,CE平分∠ACD交AB于E,∠A=128°,则∠AEC=______________.
17.如图,直线∥,△的顶点和分别落在直线和上,若∠1=60°,且∠1+∠2=90°,则的度数是______°.
18.如图,点在直线上,点在直线上,点到直线的距离为,点到直线的距离为,线段的长度为,通过测量等方法可以判断在,,三个数据中,最大的是_____________.
19.如图,长方形纸片,点,分别在边,上,连接,将对折落在直线上的点处,得折痕;将对折,点落在直线上的点得折痕,若,则____.
三、解答题
20.如图,已知、、、是正方形网格纸上的四个格点,根据要求在网格中画图并标注相关字母.
(1)画线段;
(2)画直线;
(3)过点画的垂线,垂足为;
(4)在直线上找一点,使得最小.
21.已知,如图,,,.求证:;下面是证明过,请你将它补充完整
证明:∵
∴ ( )
∴
又∵
∴
∴ ( )
∴
∵
∴
∴
∴
22.如图,,.
(1)吗?说明理由.
(2)求的度数.
23.如图,在中,垂足为点,点在边上,垂足为点.点在边上,且.求的度数.
24.如图,已知点E在直线DC上,射线EF平分,过E点作,G为射线EC上一点,连接BG,且.
(1)求证:;
(2)若,求证:.
25.已知:△ABC和平面内一点D.
(1)如图1,点D在BC边上,过D点作DE//BA交AC于点E,作DF//CA交AB于点F,判断∠EDF与∠A的数量关系,并说明理由.
(2)如图2,点D在BC的延长线上,DF//CA,∠EDF=∠A,请你判断DE与BA的位置关系.并说明理由.
(3)如图3,点D在△ABC的外部,若作DE//BA,DF//CA,请直接写出∠EDF与∠A数量关系.
26.已知:如图1,,点,分别为,上一点.
(1)在,之间有一点(点不在线段上),连接,,探究,,之间有怎样的数量关系,请补全图形,并在图形下面写出相应的数量关系,选其中一个进行证明.
(2)如图2,在,之两点,,连接,,,请选择一个图形写出,,,存在的数量关系(不需证明).
参考答案
1.D
解:A、对顶角相等,此选项正确,不符合题意;
B、两点之间所有连线中,线段最短,此选项正确,不符合题意;
C、等角的补角相等,此选项正确,不符合题意;
D、过任意一点P,能画无数条直线,此选项错误,符合题意;
2.B
解:直线外一点 P 与直线上各点连接的所有线段中,最短的是 PB ,依据是垂线段最短.
故答案选B.
3.C
解:A、∠1和∠2是同位角,故此选项不符合题意;
B、∠1和∠2是同位角,故此选项不符合题意;
C、∠1和∠2不是同位角,故此选项符合题意;
D、∠1和∠2是同位角,故此选项不符合题意;
4.C
解:A、∠D+∠DAB=180°,则AB∥DC,故选项错误;
B、∠1=∠2,则AB∥DC,故选项错误;
C、∠3=∠4,AD∥BC,故选项正确;
D、∠4=∠5,不能判定,故选项错误;
5.A
解:∵BE,CE分别平分∠ABC,∠ACD,
∴∠FBE=∠EBC,∠ACE=∠ECD,
∵EF∥BC,
∴∠FEB=∠EBC,∠ECD=∠FEC,
∴∠FBE=∠FEB,∠ACE=∠FEC,
∴BF=EF,CG=GE,
∴FG=EF-EG=7-5=2,
6.C
解:根据题意可知:∠E=60°,∠C=45°,∠1+∠2=90°,
∵,
∴∠1=60°,
∴∠1=∠E,
∴AC∥DE,
∴∠4=∠C=45°.
7.B
∵∠1=110°,纸条的两边互相平行,
∴∠4=180°-∠1=180°-110°=70°.
根据翻折的性质,
∠3=(180°-∠4)= 55°,
同理,∠2=180°-∠3=180°- 55°=125°.
8.D
∵EF∥CD
∴∠3=∠COE
∴∠3?∠1=∠COE?∠1=∠BOE
∵AB∥EF
∴∠2+∠BOE=180°,即∠2+∠3?∠1=180°
9.C
∵在同一平面内,两条直线的位置关系只有两种:相交和平行,故①不正确;
∵过直线外一点有且只有一条直线垂直于已知直线.故②不正确;
如果两条直线都与第三条直线平行,那么这两条直线也互相平行.故③正确;
从直线外一点到这条直线的垂线段的长度,叫做这点到这条直线的距离.故④不正确;
过直线外一点,有且只有一条直线与已知直线平行.故⑤不正确;
∴不正确的有①②④⑤四个.
10.B
解:A.∠A=∠BDF,由同位角相等,两直线平行,可判断DF∥AC;
B.∠2=∠4,不能判断DF∥AC;
C.∠1=∠3由内错角相等,两直线平行,可判断DF∥AC;
D.∠A+∠ADF=180°,由同旁内角互补,两直线平行,可判断DF∥AC;
11.B
解:∵
∴,
∵
∴
∴
12.D
设
则
∵
∴
∴
13.130°
解:∵OC⊥AB,
∴∠COB=90°.
∵∠EOC=40°,
∴∠BOE=∠COB?∠EOC=90°?40°=50°.
∴∠BOD=180°?∠BOE=180°?50°=130°.
14.垂线段最短
解:由题意可得,B同学跳远距离最近,所以可以确定A和C同学参加比赛,这里用到的数学原理是垂线段最短
15.70°.
解:如图,作CH∥AB,
∵AB∥CH,
∴∠B+∠BCH=180°,
∵∠ABC+∠BCD+∠CDE=360°,
∴∠D+∠DCH=180°,
∴CH∥DE,
∴AB∥DE,
∴∠1=∠3=110°,
∴∠2=180°-∠3=70°
16.26o
解:∵ABCD,
∴∠AEC=∠DCE,∠A+∠ACD=180°,
∴∠ACD=180°﹣∠A=180°﹣128°=52°,
∵CE平分∠ACD,
∴∠ACE=∠DCE==26°,
∴∠AEC=∠DCE=26°;
17.30
解:∵直线a∥b,
∴∠1=∠ACB+∠2=60°,
∵∠1=60°且∠1+∠2=90°
∴∠2=90°-60°=30°
∴∠ACB=60°-30°=30°,
18.
过点A作AD垂直于垂足为D,过点B作BH垂直于垂足为H,连接AB,
由题意得:AD=a, BH=b,AB=c;
根据点到直线垂线段最短,可知AB>AD,AB>BH
∴c>a,c>b;
∴c最大
19.
解:根据折叠可知:EM平分∠BEB′,
∴∠B′EM=∠BEM=62°15′,
∴∠AEA′=180°-2×62°15′=55°30′,
EN平分∠AEA′,
∴∠AEN=∠A′EN=∠AEA′=×55°30′=27°45′,
故答案为:27°45′.
20.
解:如图
21
证明:∵
∴(同位角相等,两直线平行)
∴(两直线平行 ,内错角相等)
又∵
∴
∴(同位角相等,两直线平行)
∴
∵
∴
∴
∴
22.
解:
(1).理由如下:
∵(已知),
∴(两直线平行,同位角相等)
(两直线平行,错角相等)
∵(已知),
∴(等量代换)
(2)∵(已知),
∴(平角的定义),
∵(已证),
∴(等量代换),
即.
23.110°
解:∵CD⊥AB,EF⊥AB
,
,
又,
,
,
又
24.
(1)∵,
∴,
∴.
又∵,
∴.
(2)∵平分,
∴.
∵,,
∴.
又∵,
∴,
∴.
25.
解:(1)∠EDF=∠A.
理由:∵DE∥BA,DF∥CA,
∴∠A=∠DEC,∠DEC=∠EDF,
∴∠A=∠EDF;
(2)DE∥BA.
证明:如图,延长BA交DF于G.
∵DF∥CA,
∴∠2=∠3.
又∵∠1=∠2,
∴∠1=∠3.
∴DE∥BA.
(3)∠EDF=∠A,∠EDF+∠A=180°.
理由:①如图,∵DE∥BA,DF∥CA,
∴∠D+∠E=180°,∠E+∠EAF=180°,
∴∠EDF=∠EAF=∠BAC;
②如图,∵DE∥BA,DF∥CA,
∴∠D+∠F=180°,∠F=∠CAB,
∴∠EDF+∠BAC=180°.
综上,∠EDF与∠A相等或互补
26.
解:(1)∠EMF=∠AEM+∠MFC.∠AEM+∠EMF+∠MFC=360°.
证明:过点M作MP∥AB.
∵AB∥CD,
∴MP∥CD.
∴∠4=∠3.
∵MP∥AB,
∴∠1=∠2.
∵∠EMF=∠2+∠3,
∴∠EMF=∠1+∠4.
∴∠EMF=∠AEM+∠MFC;
证明:过点M作MQ∥AB.
∵AB∥CD,
∴MQ∥CD.
∴∠CFM+∠1=180°;
∵MQ∥AB,
∴∠AEM+∠2=180°.
∴∠CFM+∠1+∠AEM+∠2=360°.
∵∠EMF=∠1+∠2,
∴∠AEM+∠EMF+∠MFC=360°;
(2)如图2第一个图:∠EMN+∠MNF-∠AEM-∠NFC=180°;
过点M作MP∥AB,过点N作NQ∥AB,
∴∠AEM=∠1,∠CFN=∠4,MP∥NQ,
∴∠2+∠3=180°,
∵∠EMN=∠1+∠2,∠MNF=∠3+∠4,
∴∠EMN+∠MNF=∠1+∠2+∠3+∠4,∠AEM+∠CFN=∠1+∠4,
∴∠EMN+∠MNF-∠AEM-∠NFC
=∠1+∠2+∠3+∠4-∠1-∠4
=∠2+∠3
=180°;
如图2第二个图:∠EMN-∠MNF+∠AEM+∠NFC=180°.
过点M作MP∥AB,过点N作NQ∥AB,
∴∠AEM+∠1=180°,∠CFN=∠4,MP∥NQ,
∴∠2=∠3,
∵∠EMN=∠1+∠2,∠MNF=∠3+∠4,
∴∠EMN-∠MNF=∠1+∠2-∠3-∠4,∠AEM+∠CFN=180°-∠1+∠4,
∴∠EMN-∠MNF+∠AEM+∠NFC
=∠1+∠2-∠3-∠4+180°-∠1+∠4
=180°.
