2020-2021学年苏科版数学八年级下册第9章《中心对称图形—平行四边形》常考题专练(四)(Word版 含解析)
文档属性
| 名称 | 2020-2021学年苏科版数学八年级下册第9章《中心对称图形—平行四边形》常考题专练(四)(Word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 106.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-21 22:39:54 | ||
图片预览


文档简介
八年级下册第9章《中心对称图形—平行四边形》
常考题专练(四)
1.如图,在四边形ABCD中,AB∥CD,AB=BC=2CD,E为对角线AC的中点,F为边BC的中点,连接DE、EF.
(1)求证:四边形CDEF为菱形;
(2)连接DF交AC于点G,若DF=2,CD=,求AD的长.
2.如图,在△ABC中,∠ACB=90°,D为AB边上一点,连接CD,E为CD中点,连接BE并延长至点F,使得EF=EB,连接DF交AC于点G,连接CF.
(1)求证:四边形DBCF是平行四边形;
(2)若∠A=30°,BC=4,CF=6,求CD的长.
3.如图,平行四边形ABCD中,对角线AC、BD交于点O,且AC⊥BC,点E是BC延长线上一点,,连接DE.
(1)求证:四边形ACED为矩形;
(2)连接OE,如果BD=10,求OE的长.
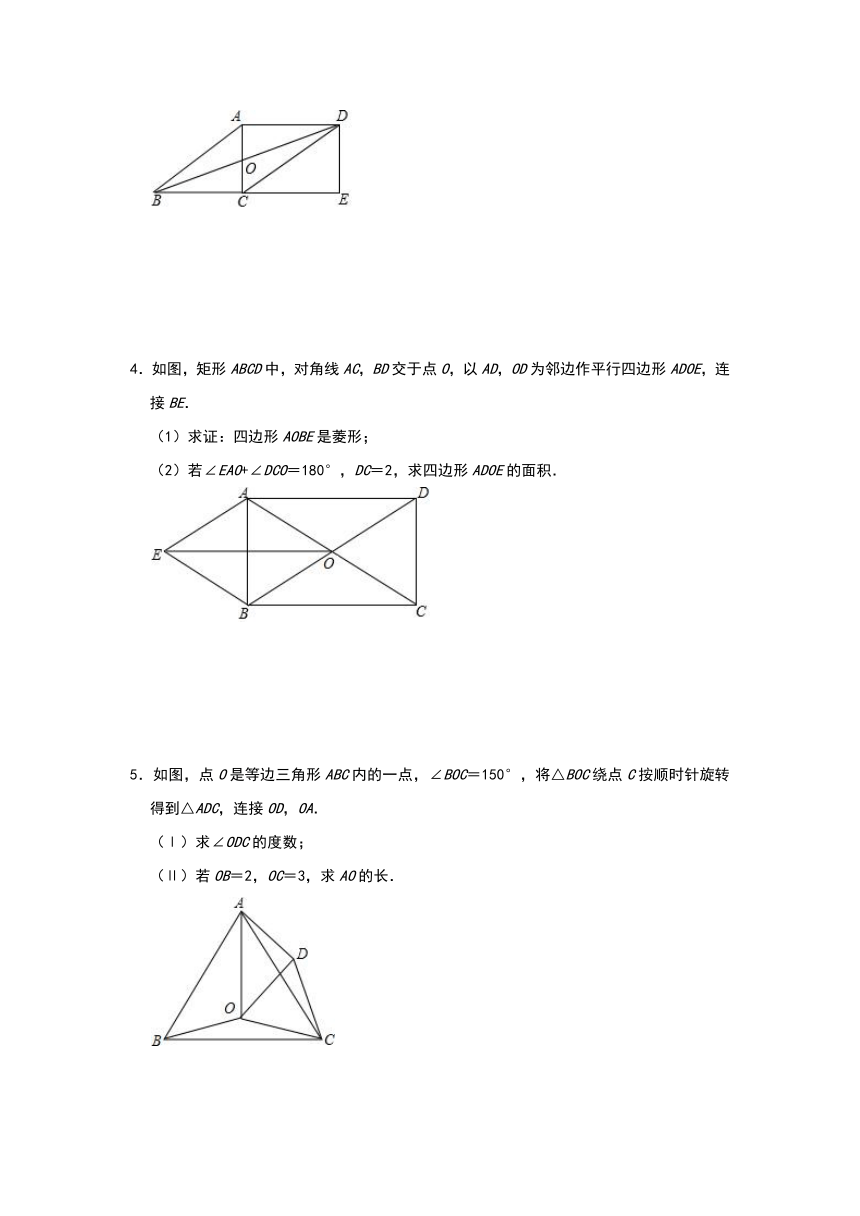
4.如图,矩形ABCD中,对角线AC,BD交于点O,以AD,OD为邻边作平行四边形ADOE,连接BE.
(1)求证:四边形AOBE是菱形;
(2)若∠EAO+∠DCO=180°,DC=2,求四边形ADOE的面积.
5.如图,点O是等边三角形ABC内的一点,∠BOC=150°,将△BOC绕点C按顺时针旋转得到△ADC,连接OD,OA.
(Ⅰ)求∠ODC的度数;
(Ⅱ)若OB=2,OC=3,求AO的长.
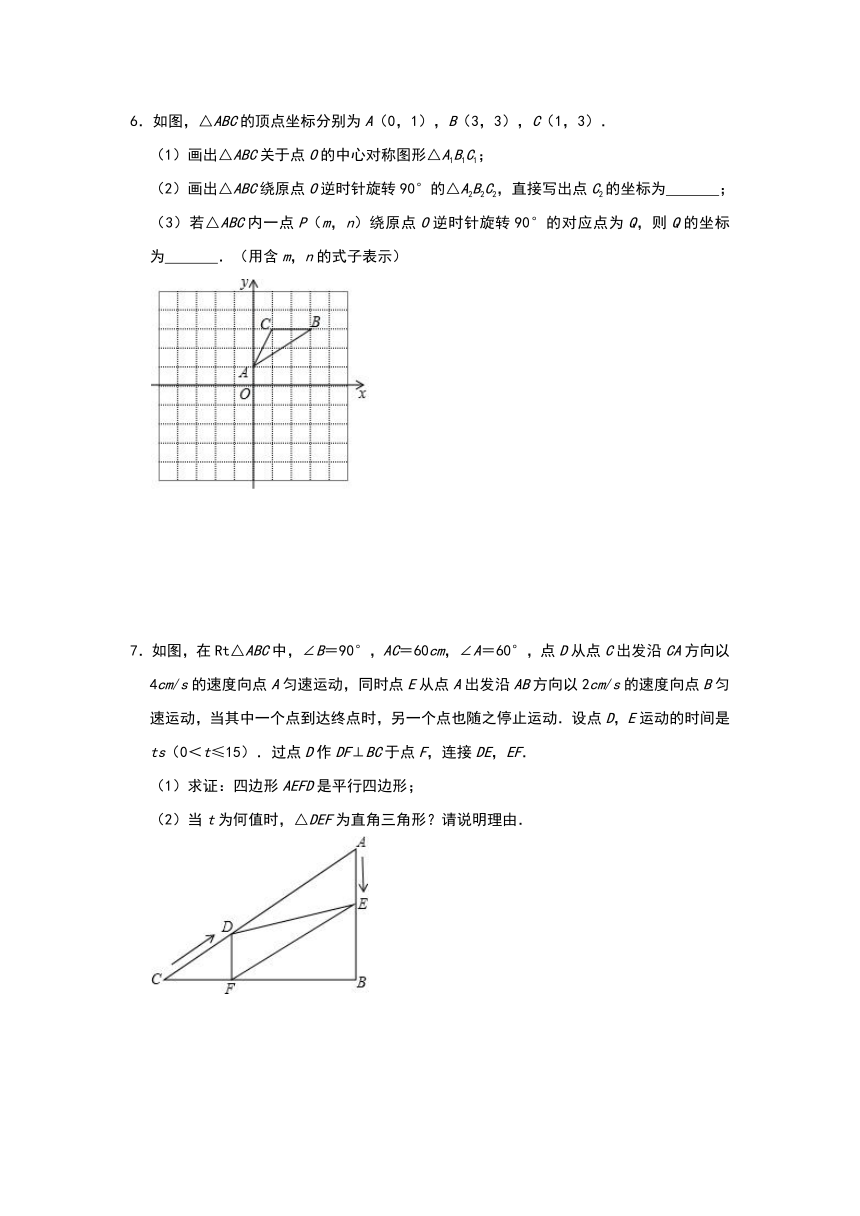
6.如图,△ABC的顶点坐标分别为A(0,1),B(3,3),C(1,3).
(1)画出△ABC关于点O的中心对称图形△A1B1C1;
(2)画出△ABC绕原点O逆时针旋转90°的△A2B2C2,直接写出点C2的坐标为
;
(3)若△ABC内一点P(m,n)绕原点O逆时针旋转90°的对应点为Q,则Q的坐标为
.(用含m,n的式子表示)
7.如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是ts(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
(1)求证:四边形AEFD是平行四边形;
(2)当t为何值时,△DEF为直角三角形?请说明理由.
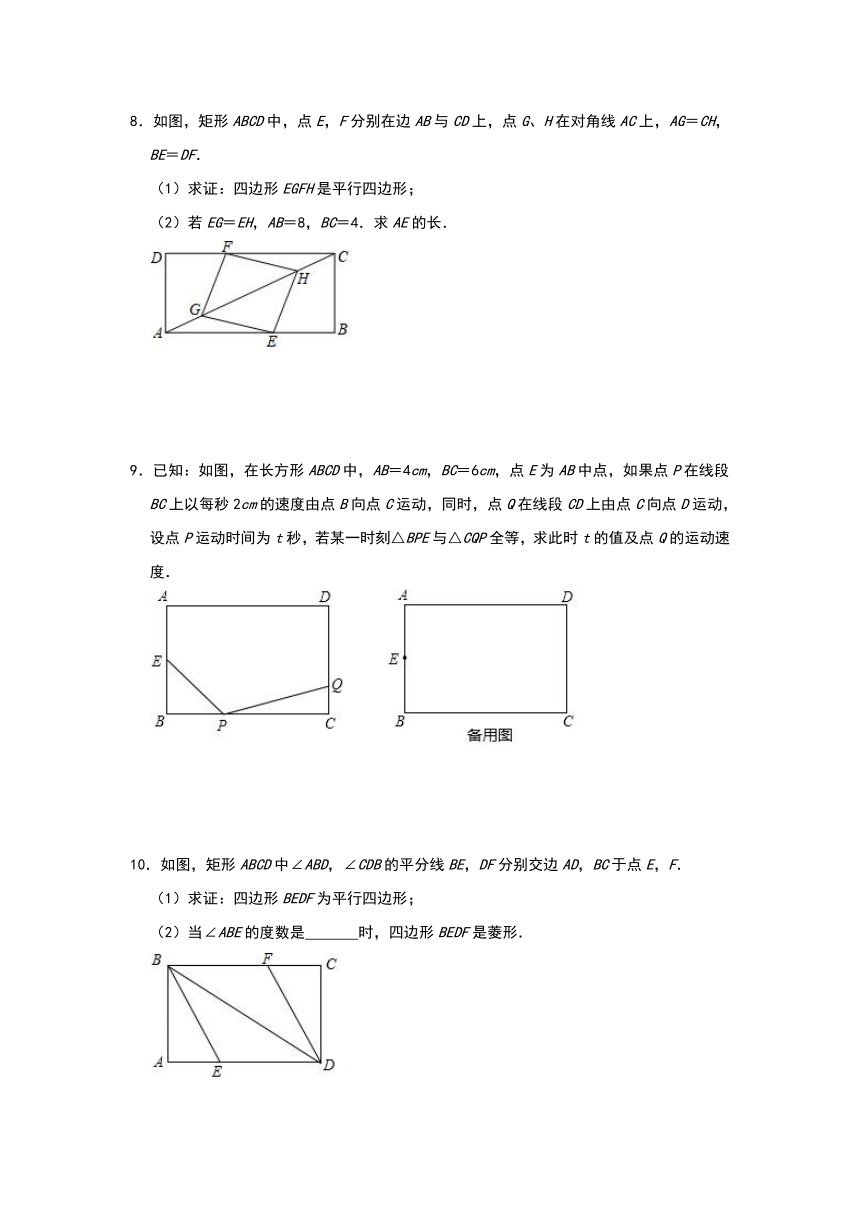
8.如图,矩形ABCD中,点E,F分别在边AB与CD上,点G、H在对角线AC上,AG=CH,BE=DF.
(1)求证:四边形EGFH是平行四边形;
(2)若EG=EH,AB=8,BC=4.求AE的长.
9.已知:如图,在长方形ABCD中,AB=4cm,BC=6cm,点E为AB中点,如果点P在线段BC上以每秒2cm的速度由点B向点C运动,同时,点Q在线段CD上由点C向点D运动,设点P运动时间为t秒,若某一时刻△BPE与△CQP全等,求此时t的值及点Q的运动速度.
10.如图,矩形ABCD中∠ABD,∠CDB的平分线BE,DF分别交边AD,BC于点E,F.
(1)求证:四边形BEDF为平行四边形;
(2)当∠ABE的度数是
时,四边形BEDF是菱形.
参考答案
1.证明:(1)∵E为对角线AC的中点,F为边BC的中点,
∴EF=AB,EF∥AB,CF=BC,AE=CE
∵AB∥CD
∴AB∥CD∥EF,
∵AB=BC=2CD
∴EF=CF=CD,且AB∥CD∥EF,
∴四边形DEFC是平行四边形,且EF=CF
∴四边形CDEF为菱形;
(2)如图,DF与EC交于点G
∵四边形CDEF为菱形,DF=2,
∴DG=1,DF⊥CE,EG=GC,
∴EG=GC==
∴AE=CE=2EG=
∴AG=AE+EG=4
∴AD==
2.证明:(1)∵点E为CD中点,
∴CE=DE.
∵EF=BE,
∴四边形DBCF是平行四边形.
(2)∵四边形DBCF是平行四边形,
∴CF∥AB,DF∥BC.
∴∠FCG=∠A=30°,∠CGF=∠CGD=∠ACB=90°.
在Rt△FCG中,CF=6,
∴,.
∵DF=BC=4,
∴DG=1.
在Rt△DCG中,CD==2
3.证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵,
∴AD=CE,
∴四边形ACED是平行四边形,
∵AC⊥BC,
∴∠ACE=90°,
∴四边形ACED是矩形;
(2)∵对角线AC,BD交于点O,
∴点O是BD的中点,
∵四边形ACED是矩形,
∴∠BED=90°,
∴OE=BD,
∴OE=5,
4.解:(1)∵四边形ABCD是矩形,∴DO=BO.
∵四边形ADOE是平行四边形,∴AE∥DO,AE=DO,AD∥OE.
∴AE∥BO,AE=BO,∴四边形AOBE是平行四边形.
∵AD⊥AB,AD∥OE,
∴AB⊥OE.
∴四边形AOBE是菱形;
(2)设AB与EO交点为M.
∵AB∥CD,∴∠DCO=∠BAO.
∵四边形AOBE是菱形,∴∠EAO=2∠BAO.
∵∠EAO+∠DCO=180°,
∴∠BAO=120°,∠EAM=60°.
又AM=AB=1,∴EM=.
∴EO=2,∴△AEO面积为×2×1=,
∴四边形ADOE面积=2.
5.解:(Ⅰ)由旋转的性质得,CD=CO,∠ACD=∠BCO,
∵∠ACB=60°,
∴∠DCO=60°,
∴△OCD为等边三角形,
∴∠ODC=60°;
(Ⅱ)由旋转的性质得,AD=OB=2,
∵△OCD为等边三角形,
∴OD=OC=3,
∵∠BOC=150°,∠ODC=60°,
∴∠ADO=90°,
在Rt△AOD中,由勾股定理得:AO==.
6.解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作,点C2的坐标为(﹣3,1);
(3)若△ABC内一点P(m,n)绕原点O逆时针旋转90°的对应点为Q,则Q的坐标为(﹣n,m).
故答案为(﹣3,1),(﹣n,m).
7.(1)证明:∵∠B=90°,∠A=60°,
∴∠C=30°,
∴AB=AC=30,
由题意得,CD=4t,AE=2t,
∵DF⊥BC,∠C=30°,
∴DF=CD=2t,
∴DF=AE,
∵DF∥AE,DF=AE,
∴四边形AEFD是平行四边形;
(2)当∠EDF=90°时,如图①,
∵DE∥BC,
∴∠ADE=∠C=30°,
∴AD=2AE,即60﹣4t=2t×2,
解得,t=,
当∠DEF=90°时,如图②,
∵AD∥EF,
∴DE⊥AC,
∴AE=2AD,即2t=2×(60﹣4t),
解得,t=12,
综上所述,当t=或12时,△DEF为直角三角形.
8.解:(1)∵矩形ABCD中,AB∥CD,
∴∠FCH=∠EAG,
又∵CD=AB,BE=DF,
∴CF=AE,
又∵CH=AG,
∴△AEG≌△CFH,
∴GE=FH,∠CHF=∠AGE,
∴∠FHG=∠EGH,
∴FH∥GE,
∴四边形EGFH是平行四边形;
(2)如图,连接EF,AF,
∵EG=EH,四边形EGFH是平行四边形,
∴四边形GFHE为菱形,
∴EF垂直平分GH,
又∵AG=CH,
∴EF垂直平分AC,
∴AF=CF=AE,
设AE=x,则FC=AF=x,DF=8﹣x,
在Rt△ADF中,AD2+DF2=AF2,
∴42+(8﹣x)2=x2,
解得x=5,
∴AE=5.
9.解:设点Q的运动速度为vcm/s,则
BP=2t,CP=6﹣2t,BE=2,CQ=vt.
由题可分两种情况:
(i)△BPE≌△CPQ,则
BP=CP,BE=CQ,
∴2t=6﹣2t,2=vt,
∴t=,v=;…(5分)
(ii)△BPE≌△CQP,则
BP=CQ,BE=CP,
∴2t=vt,2=6﹣2t.
∴t=2,v=2.…(10分)
综上所述,t的值为秒时,Q点的速度为cm/s;或t的值为2秒,Q点的速度为2
cm/s.…(11分)
10.证明:(1)∵四边形ABCD是矩形,
∴AB∥DC、AD∥BC,
∴∠ABD=∠CDB,
∵BE平分∠ABD、DF平分∠BDC,
∴∠EBD=∠ABD,∠FDB=∠BDC,
∴∠EBD=∠FDB,
∴BE∥DF,
又∵AD∥BC,
∴四边形BEDF是平行四边形;
(2)当∠ABE=30°时,四边形BEDF是菱形,
∵BE平分∠ABD,
∴∠ABD=2∠ABE=60°,∠EBD=∠ABE=30°,
∵四边形ABCD是矩形,
∴∠A=90°,
∴∠EDB=90°﹣∠ABD=30°,
∴∠EDB=∠EBD=30°,
∴EB=ED,
又∵四边形BEDF是平行四边形,
∴四边形BEDF是菱形,
故答案为:30°.
常考题专练(四)
1.如图,在四边形ABCD中,AB∥CD,AB=BC=2CD,E为对角线AC的中点,F为边BC的中点,连接DE、EF.
(1)求证:四边形CDEF为菱形;
(2)连接DF交AC于点G,若DF=2,CD=,求AD的长.
2.如图,在△ABC中,∠ACB=90°,D为AB边上一点,连接CD,E为CD中点,连接BE并延长至点F,使得EF=EB,连接DF交AC于点G,连接CF.
(1)求证:四边形DBCF是平行四边形;
(2)若∠A=30°,BC=4,CF=6,求CD的长.
3.如图,平行四边形ABCD中,对角线AC、BD交于点O,且AC⊥BC,点E是BC延长线上一点,,连接DE.
(1)求证:四边形ACED为矩形;
(2)连接OE,如果BD=10,求OE的长.
4.如图,矩形ABCD中,对角线AC,BD交于点O,以AD,OD为邻边作平行四边形ADOE,连接BE.
(1)求证:四边形AOBE是菱形;
(2)若∠EAO+∠DCO=180°,DC=2,求四边形ADOE的面积.
5.如图,点O是等边三角形ABC内的一点,∠BOC=150°,将△BOC绕点C按顺时针旋转得到△ADC,连接OD,OA.
(Ⅰ)求∠ODC的度数;
(Ⅱ)若OB=2,OC=3,求AO的长.
6.如图,△ABC的顶点坐标分别为A(0,1),B(3,3),C(1,3).
(1)画出△ABC关于点O的中心对称图形△A1B1C1;
(2)画出△ABC绕原点O逆时针旋转90°的△A2B2C2,直接写出点C2的坐标为
;
(3)若△ABC内一点P(m,n)绕原点O逆时针旋转90°的对应点为Q,则Q的坐标为
.(用含m,n的式子表示)
7.如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是ts(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
(1)求证:四边形AEFD是平行四边形;
(2)当t为何值时,△DEF为直角三角形?请说明理由.
8.如图,矩形ABCD中,点E,F分别在边AB与CD上,点G、H在对角线AC上,AG=CH,BE=DF.
(1)求证:四边形EGFH是平行四边形;
(2)若EG=EH,AB=8,BC=4.求AE的长.
9.已知:如图,在长方形ABCD中,AB=4cm,BC=6cm,点E为AB中点,如果点P在线段BC上以每秒2cm的速度由点B向点C运动,同时,点Q在线段CD上由点C向点D运动,设点P运动时间为t秒,若某一时刻△BPE与△CQP全等,求此时t的值及点Q的运动速度.
10.如图,矩形ABCD中∠ABD,∠CDB的平分线BE,DF分别交边AD,BC于点E,F.
(1)求证:四边形BEDF为平行四边形;
(2)当∠ABE的度数是
时,四边形BEDF是菱形.
参考答案
1.证明:(1)∵E为对角线AC的中点,F为边BC的中点,
∴EF=AB,EF∥AB,CF=BC,AE=CE
∵AB∥CD
∴AB∥CD∥EF,
∵AB=BC=2CD
∴EF=CF=CD,且AB∥CD∥EF,
∴四边形DEFC是平行四边形,且EF=CF
∴四边形CDEF为菱形;
(2)如图,DF与EC交于点G
∵四边形CDEF为菱形,DF=2,
∴DG=1,DF⊥CE,EG=GC,
∴EG=GC==
∴AE=CE=2EG=
∴AG=AE+EG=4
∴AD==
2.证明:(1)∵点E为CD中点,
∴CE=DE.
∵EF=BE,
∴四边形DBCF是平行四边形.
(2)∵四边形DBCF是平行四边形,
∴CF∥AB,DF∥BC.
∴∠FCG=∠A=30°,∠CGF=∠CGD=∠ACB=90°.
在Rt△FCG中,CF=6,
∴,.
∵DF=BC=4,
∴DG=1.
在Rt△DCG中,CD==2
3.证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵,
∴AD=CE,
∴四边形ACED是平行四边形,
∵AC⊥BC,
∴∠ACE=90°,
∴四边形ACED是矩形;
(2)∵对角线AC,BD交于点O,
∴点O是BD的中点,
∵四边形ACED是矩形,
∴∠BED=90°,
∴OE=BD,
∴OE=5,
4.解:(1)∵四边形ABCD是矩形,∴DO=BO.
∵四边形ADOE是平行四边形,∴AE∥DO,AE=DO,AD∥OE.
∴AE∥BO,AE=BO,∴四边形AOBE是平行四边形.
∵AD⊥AB,AD∥OE,
∴AB⊥OE.
∴四边形AOBE是菱形;
(2)设AB与EO交点为M.
∵AB∥CD,∴∠DCO=∠BAO.
∵四边形AOBE是菱形,∴∠EAO=2∠BAO.
∵∠EAO+∠DCO=180°,
∴∠BAO=120°,∠EAM=60°.
又AM=AB=1,∴EM=.
∴EO=2,∴△AEO面积为×2×1=,
∴四边形ADOE面积=2.
5.解:(Ⅰ)由旋转的性质得,CD=CO,∠ACD=∠BCO,
∵∠ACB=60°,
∴∠DCO=60°,
∴△OCD为等边三角形,
∴∠ODC=60°;
(Ⅱ)由旋转的性质得,AD=OB=2,
∵△OCD为等边三角形,
∴OD=OC=3,
∵∠BOC=150°,∠ODC=60°,
∴∠ADO=90°,
在Rt△AOD中,由勾股定理得:AO==.
6.解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作,点C2的坐标为(﹣3,1);
(3)若△ABC内一点P(m,n)绕原点O逆时针旋转90°的对应点为Q,则Q的坐标为(﹣n,m).
故答案为(﹣3,1),(﹣n,m).
7.(1)证明:∵∠B=90°,∠A=60°,
∴∠C=30°,
∴AB=AC=30,
由题意得,CD=4t,AE=2t,
∵DF⊥BC,∠C=30°,
∴DF=CD=2t,
∴DF=AE,
∵DF∥AE,DF=AE,
∴四边形AEFD是平行四边形;
(2)当∠EDF=90°时,如图①,
∵DE∥BC,
∴∠ADE=∠C=30°,
∴AD=2AE,即60﹣4t=2t×2,
解得,t=,
当∠DEF=90°时,如图②,
∵AD∥EF,
∴DE⊥AC,
∴AE=2AD,即2t=2×(60﹣4t),
解得,t=12,
综上所述,当t=或12时,△DEF为直角三角形.
8.解:(1)∵矩形ABCD中,AB∥CD,
∴∠FCH=∠EAG,
又∵CD=AB,BE=DF,
∴CF=AE,
又∵CH=AG,
∴△AEG≌△CFH,
∴GE=FH,∠CHF=∠AGE,
∴∠FHG=∠EGH,
∴FH∥GE,
∴四边形EGFH是平行四边形;
(2)如图,连接EF,AF,
∵EG=EH,四边形EGFH是平行四边形,
∴四边形GFHE为菱形,
∴EF垂直平分GH,
又∵AG=CH,
∴EF垂直平分AC,
∴AF=CF=AE,
设AE=x,则FC=AF=x,DF=8﹣x,
在Rt△ADF中,AD2+DF2=AF2,
∴42+(8﹣x)2=x2,
解得x=5,
∴AE=5.
9.解:设点Q的运动速度为vcm/s,则
BP=2t,CP=6﹣2t,BE=2,CQ=vt.
由题可分两种情况:
(i)△BPE≌△CPQ,则
BP=CP,BE=CQ,
∴2t=6﹣2t,2=vt,
∴t=,v=;…(5分)
(ii)△BPE≌△CQP,则
BP=CQ,BE=CP,
∴2t=vt,2=6﹣2t.
∴t=2,v=2.…(10分)
综上所述,t的值为秒时,Q点的速度为cm/s;或t的值为2秒,Q点的速度为2
cm/s.…(11分)
10.证明:(1)∵四边形ABCD是矩形,
∴AB∥DC、AD∥BC,
∴∠ABD=∠CDB,
∵BE平分∠ABD、DF平分∠BDC,
∴∠EBD=∠ABD,∠FDB=∠BDC,
∴∠EBD=∠FDB,
∴BE∥DF,
又∵AD∥BC,
∴四边形BEDF是平行四边形;
(2)当∠ABE=30°时,四边形BEDF是菱形,
∵BE平分∠ABD,
∴∠ABD=2∠ABE=60°,∠EBD=∠ABE=30°,
∵四边形ABCD是矩形,
∴∠A=90°,
∴∠EDB=90°﹣∠ABD=30°,
∴∠EDB=∠EBD=30°,
∴EB=ED,
又∵四边形BEDF是平行四边形,
∴四边形BEDF是菱形,
故答案为:30°.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
