2020-2021学年沪科版七年级数学下册 6.1.2立方根 专题培优训练卷(Word版 含答案)
文档属性
| 名称 | 2020-2021学年沪科版七年级数学下册 6.1.2立方根 专题培优训练卷(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 200.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-21 22:43:33 | ||
图片预览

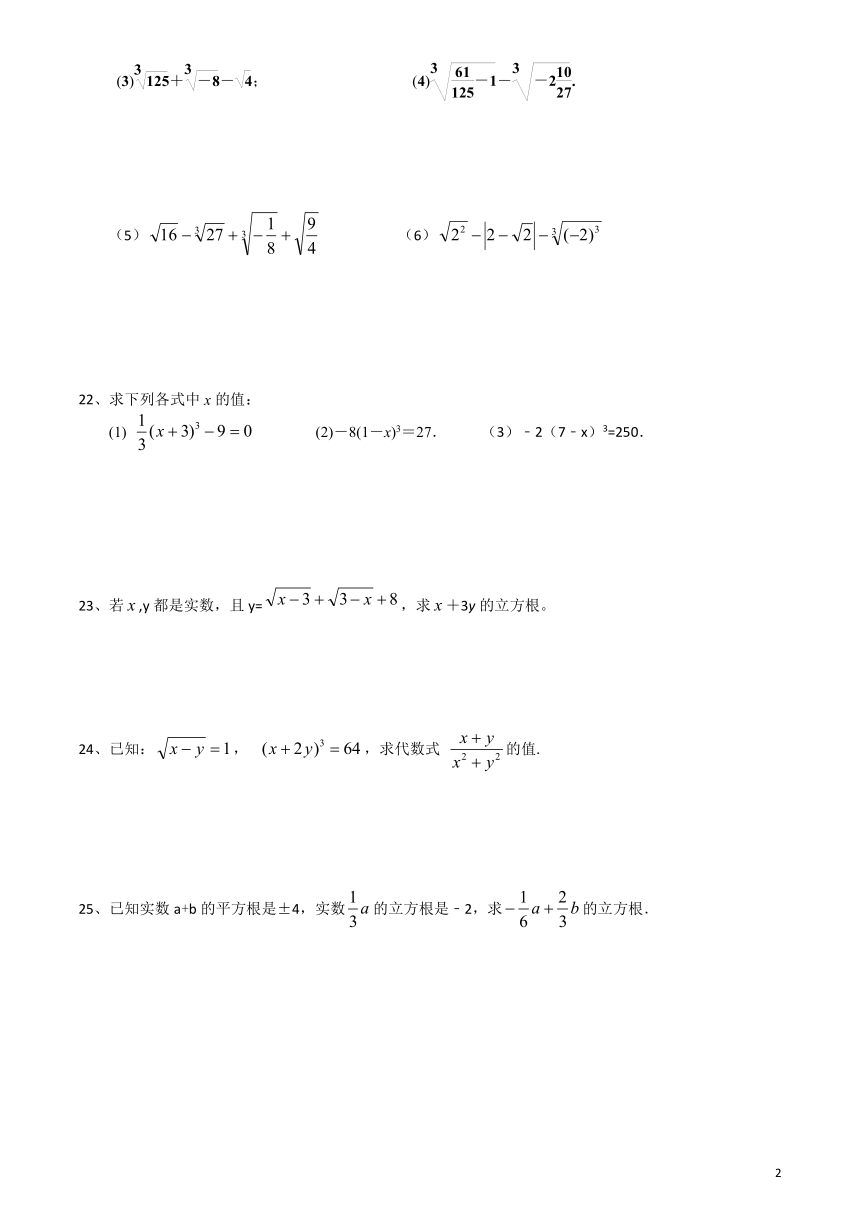
文档简介
2020-2021沪科版七年级数学下册第6章6.1.2立方根 专题培优训练卷
一、选择题
1、64的立方根为( )
A.8 B.﹣8 C.4 D.﹣4
2、的立方根是( )
A.﹣8 B.﹣4 C.﹣2 D.不存在
3、下列说法不正确的是(?? )
A.?8的立方根是2?????????????B.?-8的立方根是-2?????????????C.?0的立方根是0?????????????D.?125的立方根是±5
4、下列说法正确的是(?????)
A.?-(-8)的立方根是-2????????????????????????????????????????B.?立方根等于本身数有 -1,0,1
C.?-的立方根为-4??????????????????????????????????????????D.?一个数的立方根不是正数就是负数
5、下列说法正确的是(???)
A.?-0.064的立方根是0.4?????????????????????????????????????????B.?9的立方根是
C.?16的立方根是??????????????????????????????????????????D.?0.01的立方根是0.000001
6、的立方根是( )
A. 8 B. -8 C. 2 D. -2
7、若,则的值是(???? )
A.???????????????????????????B.?- ??????????????????????C.?± ?????????????????????D.?-
8、立方根等于它本身的有( )
A. -1,0,1 B. 0,1 C. 0,-1 D. 1
9、下列计算或说法:①±3都是27的立方根;② ;③ 的立方根是2;④ =±3,
其中正确的个数是( )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
10、已知x没有平方根,且|x|=125,则x的立方根为( )
A.?25???????????????B.?﹣25??????????????????C.?±5??????????????????????D.?﹣5
11、下列各式中,计算正确的是( )
A.=4 B.=±5 C.=1 D.=±5
12、下列说法:①任何数的平方根都有两个;②如果一个数有立方根,那么它一定有平方根;③算术平方根一定是正数;④非负数的立方根不一定是非负数.其中,错误的个数是( )
A.1 B.2 C.3 D.4
二、填空题
13、的算术平方根是?________的立方根的相反数是?________
14、(1)若+=0,则x+y=____________.
(2)已知一个有理数的平方根和立方根相同,则这个数是____________.
(3)若a是169的算术平方根,b是-125的立方根,则a+b=____________.
15、已知某正数的两个平方根分别是m+4和2m﹣16,则这个正数的立方根为_______.
16、(1)若的值为最大的负整数,则a的值是____________.
(2)若x2=64,则=____________.
17、已知 是二元一次方程组 的解,则m+3n的立方根为___3_____.
18、方程2x3+54=0的解是 .
19、已知2b+1的平方根为±3,3a+2b﹣1的算术平方根为4,则2b﹣3a的立方根是________.
20、一个正方体,它的体积是棱长为3cm的正方体体积的8倍,这个正方体的棱长是 .
三、解答题
21、计算:
(1)-; (2)+;
(3)+-; (4)-.
(5) (6)
22、求下列各式中x的值:
(1)?? (2)-8(1-x)3=27. (3)﹣2(7﹣x)3=250.
23、若,y都是实数,且?y=,求+3y的立方根。
24、已知:, ?,求代数式 的值.
25、已知实数a+b的平方根是±4,实数的立方根是﹣2,求的立方根.
2020-2021沪科版七年级数学下册第6章6.1.2立方根 专题培优训练卷(答案)
一、选择题
1、64的立方根为( )
A.8 B.﹣8 C.4 D.﹣4
【解答】解:64的立方根是4. 故选:C.
2、的立方根是( )
A.﹣8 B.﹣4 C.﹣2 D.不存在
【解答】解:∵﹣=﹣8,
∴﹣的立方根是﹣2.
故选:C.
3、下列说法不正确的是(?D? )
A.?8的立方根是2?????????????B.?-8的立方根是-2?????????????C.?0的立方根是0?????????????D.?125的立方根是±5
4、下列说法正确的是(?? B???)
A.?-(-8)的立方根是-2????????????????????????????????????????B.?立方根等于本身数有 -1,0,1
C.?-的立方根为-4??????????????????????????????????????????D.?一个数的立方根不是正数就是负数
5、下列说法正确的是(??C?)
A.?-0.064的立方根是0.4?????????????????????????????????????????B.?9的立方根是
C.?16的立方根是??????????????????????????????????????????D.?0.01的立方根是0.000001
6、的立方根是( D )
A. 8 B. -8 C. 2 D. -2
7、若,则的值是(???B?? )
A.???????????????????????????B.?- ??????????????????????C.?± ?????????????????????D.?-
8、立方根等于它本身的有( A)
A. -1,0,1 B. 0,1 C. 0,-1 D. 1
9、下列计算或说法:①±3都是27的立方根;② ;③ 的立方根是2;④ =±3,
其中正确的个数是( B )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
10、已知x没有平方根,且|x|=125,则x的立方根为( D )
A.?25???????????????B.?﹣25??????????????????C.?±5??????????????????????D.?﹣5
11、下列各式中,计算正确的是( )
A.=4 B.=±5 C.=1 D.=±5
【解答】解:A、=4,正确;
B、=5,故错误;
C、=﹣1,故错误;
D、=5,故错误;
故选:A.
12、下列说法:①任何数的平方根都有两个;②如果一个数有立方根,那么它一定有平方根;③算术平方根一定是正数;④非负数的立方根不一定是非负数.其中,错误的个数是( )
A.1 B.2 C.3 D.4
【解答】解:①0的平方根只有一个,故任何数的平方根都有两个结论错误,
②负数有立方根,但是没有平方根,故如果一个数有立方根,那么它一定有平方根结论错误,
③算术平方根还可能是0,故算术平方根一定是正数结论错误,
④非负数的立方根一定是非负数,故非负数的立方根不一定是非负数,
错误的结论①②③④,故选:D.
二、填空题
13、的算术平方根是?________的立方根的相反数是?________
答案:2;-2
14、(1)若+=0,则x+y=____________.
(2)已知一个有理数的平方根和立方根相同,则这个数是____________.
(3)若a是169的算术平方根,b是-125的立方根,则a+b=____________.
答案: (1)0 (2)0 (3)8
15、已知某正数的两个平方根分别是m+4和2m﹣16,则这个正数的立方根为___4 _____.
16、(1)若的值为最大的负整数,则a的值是____________.
(2)若x2=64,则=____________.
答案:(1)±4 (2)±2
17、已知 是二元一次方程组 的解,则m+3n的立方根为___3_____.
18、方程2x3+54=0的解是 .
【解答】解:方程整理得:x3=﹣27,
开立方得:x=﹣3.
故答案为:x=﹣3.
19、已知2b+1的平方根为±3,3a+2b﹣1的算术平方根为4,则2b﹣3a的立方根是___-1 _____.
20、一个正方体,它的体积是棱长为3cm的正方体体积的8倍,这个正方体的棱长是 .
【解答】解:根据题意得: =6(cm),
故答案为:6cm
三、解答题
21、计算:
(1)-; (2)+;
(3)+-; (4)-.
(5) (6)
解: (1)- (2)6 (3)1 (4)
(5)原式=4﹣3﹣ + =5﹣3=2
(6)原式=2﹣2+ ?+2=2+ .
22、求下列各式中x的值:
(1)?? (2)-8(1-x)3=27. (3)﹣2(7﹣x)3=250.
解:(1)∵,
∴(x+3)3=27,
∴x+3=3,
解得x=0.
(2)-8(1-x)3=27,
-2(1-x)=3,
1-x=-1.5,
?x=2.5.
(3)﹣2(7﹣x)3=250,
两边同时除以﹣2,得(7﹣x)3=﹣125,
∴7﹣x=﹣5,∴x=12.
23、若,y都是实数,且?y=,求+3y的立方根。
解:由题意可知,
解得:x=3,则y=8,x+3y=27,故x+3y的立方根是3.
24、已知:, ?,求代数式 的值.
解:由题意得: ,解得 ,
∴ = =
25、已知实数a+b的平方根是±4,实数的立方根是﹣2,求的立方根.
【解答】解:∵实数a+b的平方根是±4,实数的立方根是﹣2,
∴a+b=16, =﹣8,
∴a=﹣24,b=40,
∴﹣a+b==,
∴﹣a+b的立方根.
一、选择题
1、64的立方根为( )
A.8 B.﹣8 C.4 D.﹣4
2、的立方根是( )
A.﹣8 B.﹣4 C.﹣2 D.不存在
3、下列说法不正确的是(?? )
A.?8的立方根是2?????????????B.?-8的立方根是-2?????????????C.?0的立方根是0?????????????D.?125的立方根是±5
4、下列说法正确的是(?????)
A.?-(-8)的立方根是-2????????????????????????????????????????B.?立方根等于本身数有 -1,0,1
C.?-的立方根为-4??????????????????????????????????????????D.?一个数的立方根不是正数就是负数
5、下列说法正确的是(???)
A.?-0.064的立方根是0.4?????????????????????????????????????????B.?9的立方根是
C.?16的立方根是??????????????????????????????????????????D.?0.01的立方根是0.000001
6、的立方根是( )
A. 8 B. -8 C. 2 D. -2
7、若,则的值是(???? )
A.???????????????????????????B.?- ??????????????????????C.?± ?????????????????????D.?-
8、立方根等于它本身的有( )
A. -1,0,1 B. 0,1 C. 0,-1 D. 1
9、下列计算或说法:①±3都是27的立方根;② ;③ 的立方根是2;④ =±3,
其中正确的个数是( )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
10、已知x没有平方根,且|x|=125,则x的立方根为( )
A.?25???????????????B.?﹣25??????????????????C.?±5??????????????????????D.?﹣5
11、下列各式中,计算正确的是( )
A.=4 B.=±5 C.=1 D.=±5
12、下列说法:①任何数的平方根都有两个;②如果一个数有立方根,那么它一定有平方根;③算术平方根一定是正数;④非负数的立方根不一定是非负数.其中,错误的个数是( )
A.1 B.2 C.3 D.4
二、填空题
13、的算术平方根是?________的立方根的相反数是?________
14、(1)若+=0,则x+y=____________.
(2)已知一个有理数的平方根和立方根相同,则这个数是____________.
(3)若a是169的算术平方根,b是-125的立方根,则a+b=____________.
15、已知某正数的两个平方根分别是m+4和2m﹣16,则这个正数的立方根为_______.
16、(1)若的值为最大的负整数,则a的值是____________.
(2)若x2=64,则=____________.
17、已知 是二元一次方程组 的解,则m+3n的立方根为___3_____.
18、方程2x3+54=0的解是 .
19、已知2b+1的平方根为±3,3a+2b﹣1的算术平方根为4,则2b﹣3a的立方根是________.
20、一个正方体,它的体积是棱长为3cm的正方体体积的8倍,这个正方体的棱长是 .
三、解答题
21、计算:
(1)-; (2)+;
(3)+-; (4)-.
(5) (6)
22、求下列各式中x的值:
(1)?? (2)-8(1-x)3=27. (3)﹣2(7﹣x)3=250.
23、若,y都是实数,且?y=,求+3y的立方根。
24、已知:, ?,求代数式 的值.
25、已知实数a+b的平方根是±4,实数的立方根是﹣2,求的立方根.
2020-2021沪科版七年级数学下册第6章6.1.2立方根 专题培优训练卷(答案)
一、选择题
1、64的立方根为( )
A.8 B.﹣8 C.4 D.﹣4
【解答】解:64的立方根是4. 故选:C.
2、的立方根是( )
A.﹣8 B.﹣4 C.﹣2 D.不存在
【解答】解:∵﹣=﹣8,
∴﹣的立方根是﹣2.
故选:C.
3、下列说法不正确的是(?D? )
A.?8的立方根是2?????????????B.?-8的立方根是-2?????????????C.?0的立方根是0?????????????D.?125的立方根是±5
4、下列说法正确的是(?? B???)
A.?-(-8)的立方根是-2????????????????????????????????????????B.?立方根等于本身数有 -1,0,1
C.?-的立方根为-4??????????????????????????????????????????D.?一个数的立方根不是正数就是负数
5、下列说法正确的是(??C?)
A.?-0.064的立方根是0.4?????????????????????????????????????????B.?9的立方根是
C.?16的立方根是??????????????????????????????????????????D.?0.01的立方根是0.000001
6、的立方根是( D )
A. 8 B. -8 C. 2 D. -2
7、若,则的值是(???B?? )
A.???????????????????????????B.?- ??????????????????????C.?± ?????????????????????D.?-
8、立方根等于它本身的有( A)
A. -1,0,1 B. 0,1 C. 0,-1 D. 1
9、下列计算或说法:①±3都是27的立方根;② ;③ 的立方根是2;④ =±3,
其中正确的个数是( B )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
10、已知x没有平方根,且|x|=125,则x的立方根为( D )
A.?25???????????????B.?﹣25??????????????????C.?±5??????????????????????D.?﹣5
11、下列各式中,计算正确的是( )
A.=4 B.=±5 C.=1 D.=±5
【解答】解:A、=4,正确;
B、=5,故错误;
C、=﹣1,故错误;
D、=5,故错误;
故选:A.
12、下列说法:①任何数的平方根都有两个;②如果一个数有立方根,那么它一定有平方根;③算术平方根一定是正数;④非负数的立方根不一定是非负数.其中,错误的个数是( )
A.1 B.2 C.3 D.4
【解答】解:①0的平方根只有一个,故任何数的平方根都有两个结论错误,
②负数有立方根,但是没有平方根,故如果一个数有立方根,那么它一定有平方根结论错误,
③算术平方根还可能是0,故算术平方根一定是正数结论错误,
④非负数的立方根一定是非负数,故非负数的立方根不一定是非负数,
错误的结论①②③④,故选:D.
二、填空题
13、的算术平方根是?________的立方根的相反数是?________
答案:2;-2
14、(1)若+=0,则x+y=____________.
(2)已知一个有理数的平方根和立方根相同,则这个数是____________.
(3)若a是169的算术平方根,b是-125的立方根,则a+b=____________.
答案: (1)0 (2)0 (3)8
15、已知某正数的两个平方根分别是m+4和2m﹣16,则这个正数的立方根为___4 _____.
16、(1)若的值为最大的负整数,则a的值是____________.
(2)若x2=64,则=____________.
答案:(1)±4 (2)±2
17、已知 是二元一次方程组 的解,则m+3n的立方根为___3_____.
18、方程2x3+54=0的解是 .
【解答】解:方程整理得:x3=﹣27,
开立方得:x=﹣3.
故答案为:x=﹣3.
19、已知2b+1的平方根为±3,3a+2b﹣1的算术平方根为4,则2b﹣3a的立方根是___-1 _____.
20、一个正方体,它的体积是棱长为3cm的正方体体积的8倍,这个正方体的棱长是 .
【解答】解:根据题意得: =6(cm),
故答案为:6cm
三、解答题
21、计算:
(1)-; (2)+;
(3)+-; (4)-.
(5) (6)
解: (1)- (2)6 (3)1 (4)
(5)原式=4﹣3﹣ + =5﹣3=2
(6)原式=2﹣2+ ?+2=2+ .
22、求下列各式中x的值:
(1)?? (2)-8(1-x)3=27. (3)﹣2(7﹣x)3=250.
解:(1)∵,
∴(x+3)3=27,
∴x+3=3,
解得x=0.
(2)-8(1-x)3=27,
-2(1-x)=3,
1-x=-1.5,
?x=2.5.
(3)﹣2(7﹣x)3=250,
两边同时除以﹣2,得(7﹣x)3=﹣125,
∴7﹣x=﹣5,∴x=12.
23、若,y都是实数,且?y=,求+3y的立方根。
解:由题意可知,
解得:x=3,则y=8,x+3y=27,故x+3y的立方根是3.
24、已知:, ?,求代数式 的值.
解:由题意得: ,解得 ,
∴ = =
25、已知实数a+b的平方根是±4,实数的立方根是﹣2,求的立方根.
【解答】解:∵实数a+b的平方根是±4,实数的立方根是﹣2,
∴a+b=16, =﹣8,
∴a=﹣24,b=40,
∴﹣a+b==,
∴﹣a+b的立方根.
