6.4.1 平面几何中的向量方法 电子教案(表格式)
文档属性
| 名称 | 6.4.1 平面几何中的向量方法 电子教案(表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 234.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-22 19:47:50 | ||
图片预览


文档简介
11988800122936006.4.1 平面几何中的向量方法
本节课选自《普通高中课程标准数学教科书-必修第二册》(人教A版)第六章《平面向量及其应用,本节课主要学习用向量解决平面几何问题,进一步加深对向量工具性的理解。
8350251232535本节的目的是让学生加深对向量的认识,更好地体会向量这个工具的优越性.对于向量方法,就思路而言,几何中的向量方法完全与几何中的代数方法一致,不同的只是用“向量和向量运算”来代替“数和数的运算”.这就是把点、线、面等几何要素直接归结为向量,对这些向量借助于它们之间的运算进行讨论,然后把这些计算结果翻译成关于点、线、面的相应结果.代数方法的流程图可以简单地表述为:
233362573025则向量方法的流程图可以简单地表述为:
这就是本节给出的用向量方法解决几何问题的“三步曲”,也是本节的重点.
课程目标
学科素养
A.通过平行四边形这个几何模型,归纳总结出用向量方法解决平面几何的问题的”三步曲”;
B.明确平面几何图形中的有关性质,如平移、全等、相似、长度、夹角等可以由向量的线性运算及数量积表示;
C.让学生深刻理解向量在处理平面几何问题中的优越性.
1.数学抽象:平面几何图形中的有关性质,如平移、全等、相似、长度、夹角等可以由向量的线性运算及数量积表示;
2.逻辑推理:用向量方法解决平面几何的问题的”三步曲”;
3.数学运算:向量的线性运算及数量积表示;
4. 直观想象:向量在处理平面几何问题中的优越性;
5. 数学建模:通过向量运算的学习理解和体验实际问题抽象为数学概念的过程和思想,增强数学的应用意识。
1.教学重点:用向量方法解决实际问题的基本方法:向量法解决几何问题的“三步曲”;
2.教学难点:如何将几何等实际问题化归为向量问题.
多媒体
教学过程
教学设计意图
核心素养目标
复习回顾,情境引入
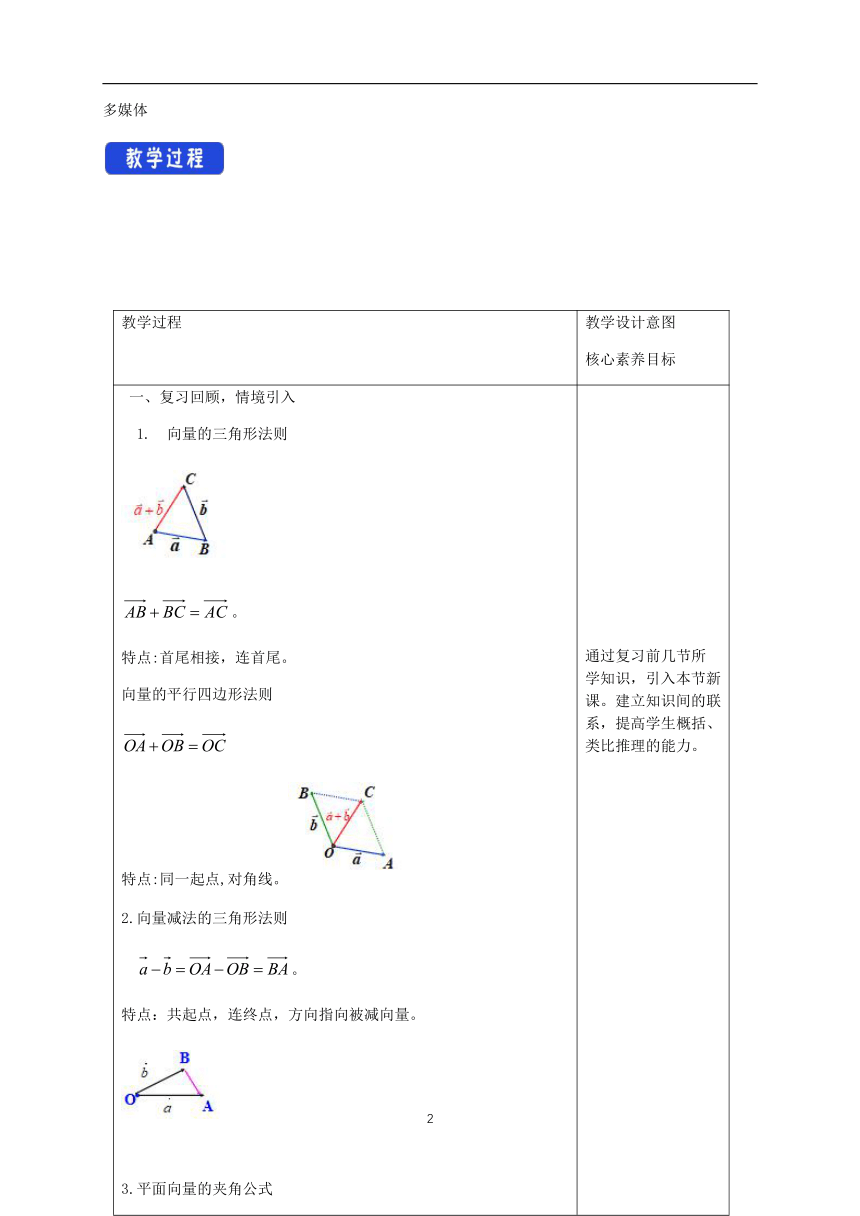
向量的三角形法则
false。
特点:首尾相接,连首尾。
向量的平行四边形法则
false
特点:同一起点,对角线。
2.向量减法的三角形法则
false。
特点:共起点,连终点,方向指向被减向量。
3.平面向量的夹角公式
false
4.模
false
5.共线向量定理
false
6.由于向量的线性运算和数量积运算具有鲜明的几何背景,平面几何的许多性质,如平移、全等、相似、长度、夹角都可以由向量的线性运算及数量积表示出来,因此,利用向量方法可以解决平面几何中的一些问题.
二、探索新知
2607945445135例1.如图6.4-1,DE是false的中位线,用向量方法证明:false.
思考:运用向量方法解决平面几何问题可以分哪几个步骤?
“三步曲”:
(1)建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题;
(2)通过向量运算,研究几何元素之间的关系,如距离、夹角等问题;
(3)把运算结果“翻译”成几何关系.
例2.如图,已知平行四边形ABCD,你能发现对角线AC和BD的长度与两条邻边AB和AD的长度之间的关系吗?2470785347980
通过复习前几节所学知识,引入本节新课。建立知识间的联系,提高学生概括、类比推理的能力。
通过例题让学生了解用向量方法证明几何问题,提高学生的解决问题、分析问题的能力。
通过思考,总结用向量方法做几何问题的步骤,提高学生分析问题、概括问题的能力。
通过例题进一步熟悉向量的工具作用,提高学生用向量解决几何知识解决问题的能力。
三、达标检测
1.已知在△ABC中,若=a,=b,且a·b<0,则△ABC的形状为( )
A.钝角三角形 B.直角三角形
C.锐角三角形 D.不能确定
答案 A
2.在直角三角形ABC中,斜边BC长为2,O是平面ABC内一点,点P满足=+(+),则||等于( )
A.2 B.1 C. D.4
答案 B
解析 ∵=+(+),
∴-=(+),=(+),
∴AP为Rt△ABC斜边BC的中线.∴||=1.
3.如图,在平行四边形ABCD中,已知AB=8,AD=5,=3,·=2,则·的值是________.
答案 22
解析 由=3,得==,=+=+,=-=+-=-.因为·=2,所以·=2,即2-·-2=2.又因为2=25,2=64,所以·=22.
4.如图所示,在△ABC中,点O是BC的中点.过点O的直线分别交直线AB,AC于不同的两点M,N,若=m,=n,则m+n的值为________.
答案 2
解析 ∵O是BC的中点,∴=(+).
又∵=m,=n,∴=+.
又∵M,O,N三点共线,∴+=1,则m+n=2.
通过练习巩固本节所学知识,通过学生解决问题的能力,感悟其中蕴含的数学思想,增强学生的应用意识。
四、小结
1. 向量的有关知识;2.用向量解决几何问题的步骤;
五、作业
习题6.4 1,3题
通过总结,让学生进一步巩固本节所学内容,提高概括能力,提高学生的数学运算能力和逻辑推理能力。
在整个教学过程中,首先检查学生对学案的完成程度,大部分学生基本能按要求完成,少部分基础较弱的没有完成紧接着提出向量的几何背景,提出平面几何问题是否可用向量知识来处理.在这一背景下提出了(例1),对这个问题的解决,我的做法是充分让学生分析用向量方法解决这一几何
问题的过程,并归纳出用向量方法解决平面几何问题的一般步骤,当然在探究过程中学生可能会分析得不到位和归纳不全面,教师应适当引导和完善问题的解答,在这一问题的设计上,以分析几个小问题的形式完成对问题2的整个探究过程,把一个大问题分解成几个小问题来引导,那学生探究起来会更容易一些,并且从中都是以学生为主开展的,体现了以学生为主体,教师为主导的教学理念。
本节课选自《普通高中课程标准数学教科书-必修第二册》(人教A版)第六章《平面向量及其应用,本节课主要学习用向量解决平面几何问题,进一步加深对向量工具性的理解。
8350251232535本节的目的是让学生加深对向量的认识,更好地体会向量这个工具的优越性.对于向量方法,就思路而言,几何中的向量方法完全与几何中的代数方法一致,不同的只是用“向量和向量运算”来代替“数和数的运算”.这就是把点、线、面等几何要素直接归结为向量,对这些向量借助于它们之间的运算进行讨论,然后把这些计算结果翻译成关于点、线、面的相应结果.代数方法的流程图可以简单地表述为:
233362573025则向量方法的流程图可以简单地表述为:
这就是本节给出的用向量方法解决几何问题的“三步曲”,也是本节的重点.
课程目标
学科素养
A.通过平行四边形这个几何模型,归纳总结出用向量方法解决平面几何的问题的”三步曲”;
B.明确平面几何图形中的有关性质,如平移、全等、相似、长度、夹角等可以由向量的线性运算及数量积表示;
C.让学生深刻理解向量在处理平面几何问题中的优越性.
1.数学抽象:平面几何图形中的有关性质,如平移、全等、相似、长度、夹角等可以由向量的线性运算及数量积表示;
2.逻辑推理:用向量方法解决平面几何的问题的”三步曲”;
3.数学运算:向量的线性运算及数量积表示;
4. 直观想象:向量在处理平面几何问题中的优越性;
5. 数学建模:通过向量运算的学习理解和体验实际问题抽象为数学概念的过程和思想,增强数学的应用意识。
1.教学重点:用向量方法解决实际问题的基本方法:向量法解决几何问题的“三步曲”;
2.教学难点:如何将几何等实际问题化归为向量问题.
多媒体
教学过程
教学设计意图
核心素养目标
复习回顾,情境引入
向量的三角形法则
false。
特点:首尾相接,连首尾。
向量的平行四边形法则
false
特点:同一起点,对角线。
2.向量减法的三角形法则
false。
特点:共起点,连终点,方向指向被减向量。
3.平面向量的夹角公式
false
4.模
false
5.共线向量定理
false
6.由于向量的线性运算和数量积运算具有鲜明的几何背景,平面几何的许多性质,如平移、全等、相似、长度、夹角都可以由向量的线性运算及数量积表示出来,因此,利用向量方法可以解决平面几何中的一些问题.
二、探索新知
2607945445135例1.如图6.4-1,DE是false的中位线,用向量方法证明:false.
思考:运用向量方法解决平面几何问题可以分哪几个步骤?
“三步曲”:
(1)建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题;
(2)通过向量运算,研究几何元素之间的关系,如距离、夹角等问题;
(3)把运算结果“翻译”成几何关系.
例2.如图,已知平行四边形ABCD,你能发现对角线AC和BD的长度与两条邻边AB和AD的长度之间的关系吗?2470785347980
通过复习前几节所学知识,引入本节新课。建立知识间的联系,提高学生概括、类比推理的能力。
通过例题让学生了解用向量方法证明几何问题,提高学生的解决问题、分析问题的能力。
通过思考,总结用向量方法做几何问题的步骤,提高学生分析问题、概括问题的能力。
通过例题进一步熟悉向量的工具作用,提高学生用向量解决几何知识解决问题的能力。
三、达标检测
1.已知在△ABC中,若=a,=b,且a·b<0,则△ABC的形状为( )
A.钝角三角形 B.直角三角形
C.锐角三角形 D.不能确定
答案 A
2.在直角三角形ABC中,斜边BC长为2,O是平面ABC内一点,点P满足=+(+),则||等于( )
A.2 B.1 C. D.4
答案 B
解析 ∵=+(+),
∴-=(+),=(+),
∴AP为Rt△ABC斜边BC的中线.∴||=1.
3.如图,在平行四边形ABCD中,已知AB=8,AD=5,=3,·=2,则·的值是________.
答案 22
解析 由=3,得==,=+=+,=-=+-=-.因为·=2,所以·=2,即2-·-2=2.又因为2=25,2=64,所以·=22.
4.如图所示,在△ABC中,点O是BC的中点.过点O的直线分别交直线AB,AC于不同的两点M,N,若=m,=n,则m+n的值为________.
答案 2
解析 ∵O是BC的中点,∴=(+).
又∵=m,=n,∴=+.
又∵M,O,N三点共线,∴+=1,则m+n=2.
通过练习巩固本节所学知识,通过学生解决问题的能力,感悟其中蕴含的数学思想,增强学生的应用意识。
四、小结
1. 向量的有关知识;2.用向量解决几何问题的步骤;
五、作业
习题6.4 1,3题
通过总结,让学生进一步巩固本节所学内容,提高概括能力,提高学生的数学运算能力和逻辑推理能力。
在整个教学过程中,首先检查学生对学案的完成程度,大部分学生基本能按要求完成,少部分基础较弱的没有完成紧接着提出向量的几何背景,提出平面几何问题是否可用向量知识来处理.在这一背景下提出了(例1),对这个问题的解决,我的做法是充分让学生分析用向量方法解决这一几何
问题的过程,并归纳出用向量方法解决平面几何问题的一般步骤,当然在探究过程中学生可能会分析得不到位和归纳不全面,教师应适当引导和完善问题的解答,在这一问题的设计上,以分析几个小问题的形式完成对问题2的整个探究过程,把一个大问题分解成几个小问题来引导,那学生探究起来会更容易一些,并且从中都是以学生为主开展的,体现了以学生为主体,教师为主导的教学理念。
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
