8.1 基本几何图形 第2课时 圆柱、圆锥、圆台、球、简单组合体 电子教案(表格式)
文档属性
| 名称 | 8.1 基本几何图形 第2课时 圆柱、圆锥、圆台、球、简单组合体 电子教案(表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 340.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-22 19:55:46 | ||
图片预览


文档简介
【新教材】8.1 基本几何图形 教学设计(人教A版)
第2课时 圆柱、圆锥、圆台、球、简单组合体
立体几何是研究三维空间中物体的形状、大小、位置关系的一门数学学科,而三维空间是人们生存发展的现实空间,学习立体几何对我们更好地认识客观世界,更好地生存与发展具有重要意义。在立体几何初步部分,学生将先从对空间几何体观察入手、认识空间图形;再以长方体为载体,直观认识和理解空间点、线、面的位置关系。本节内容既是义务教育阶段“空间与图形”课程的延续和提高,也是后续研究空间点、线、面位置关系的基础,既巩固了前面所学的内容,又为后面内容的学习做了知识上和方法上的准备,在教材中起着承前启后的作用。
课程目标
1.认识圆柱、圆锥、圆台、球的结构特征.
2.认识柱、锥、台、球及其简单组合体的结构特征,并能运用这些特征描述现实生活中简单物体的结构.
数学学科素养
1.数学抽象:简单组合体概念的理解;
2.逻辑推理:圆柱、圆锥、圆台、球的结构特点;
3.直观想象:判断空间几何体;
4.数学运算:球的相关计算、最短距离等;
5.数学建模:通过平面展开图将空间问题转化为平面问题解决,体现了转化的思想方法.
重点:掌握圆柱、圆锥、圆台、球的结构特征;
难点:旋转体的相关计算.
教学方法:以学生为主体,小组为单位,采用诱思探究式教学,精讲多练。
教学工具:多媒体。
情景导入
上节课学了常见的多面体:棱柱、棱锥、棱台,那么常见的旋转体有哪些?又有什么结构特点?
要求:让学生自由发言,教师不做判断。而是引导学生进一步观察.研探.
二、预习课本,引入新课
阅读课本101-104页,思考并完成以下问题
1、旋转体包含哪些图形?
2、圆柱、圆锥、圆台、球是怎样定义的?又有什么结构特点?
3、什么是简单组合体,特点是什么?
要求:学生独立完成,以小组为单位,组内可商量,最终选出代表回答问题。
三、新知探究
一、常见的旋转体
1、圆柱:
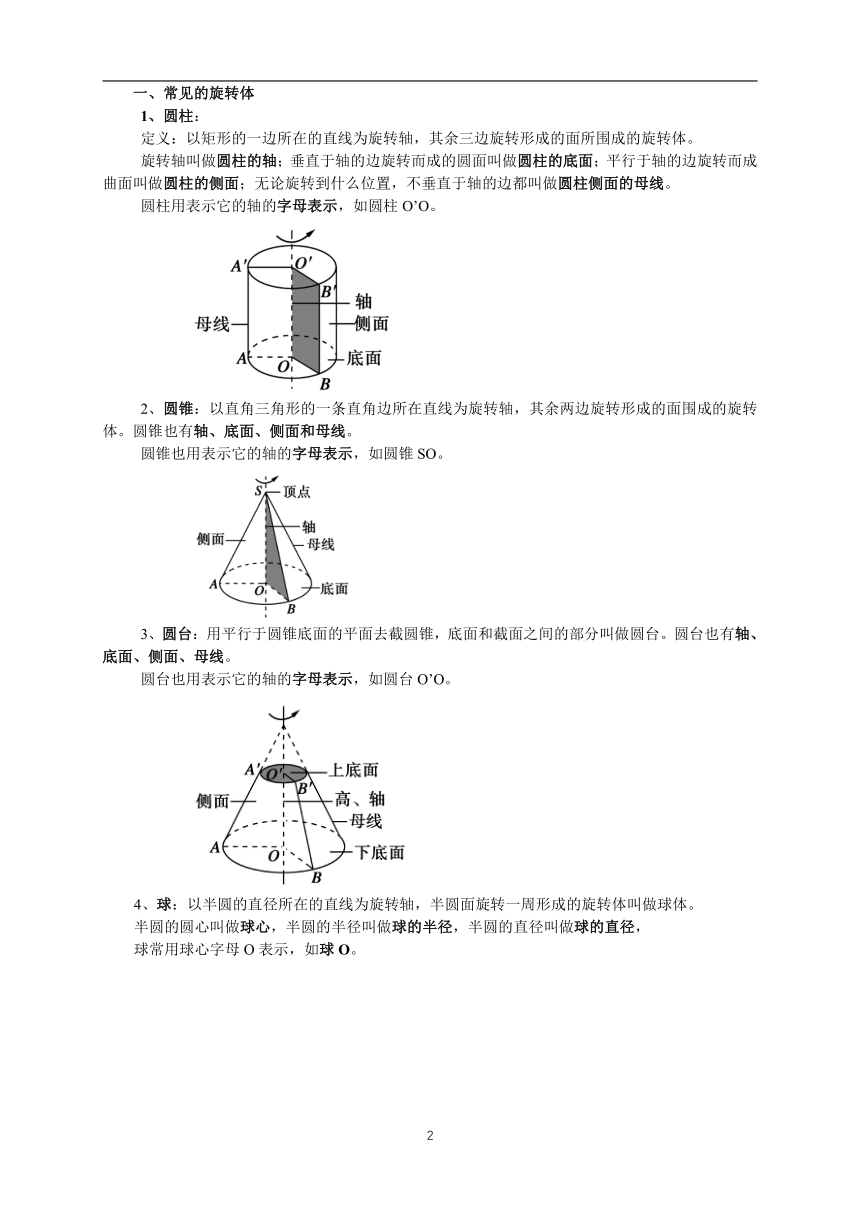
定义:以矩形的一边所在的直线为旋转轴,其余三边旋转形成的面所围成的旋转体。
旋转轴叫做圆柱的轴;垂直于轴的边旋转而成的圆面叫做圆柱的底面;平行于轴的边旋转而成曲面叫做圆柱的侧面;无论旋转到什么位置,不垂直于轴的边都叫做圆柱侧面的母线。
圆柱用表示它的轴的字母表示,如圆柱O’O。
2、圆锥:以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的面围成的旋转体。圆锥也有轴、底面、侧面和母线。
圆锥也用表示它的轴的字母表示,如圆锥SO。
3、圆台:用平行于圆锥底面的平面去截圆锥,底面和截面之间的部分叫做圆台。圆台也有轴、底面、侧面、母线。
圆台也用表示它的轴的字母表示,如圆台O’O。
4、球:以半圆的直径所在的直线为旋转轴,半圆面旋转一周形成的旋转体叫做球体。
半圆的圆心叫做球心,半圆的半径叫做球的半径,半圆的直径叫做球的直径,
球常用球心字母O表示,如球O。
小结:常见空间几何体有棱柱、棱锥、棱台、圆柱、圆锥、圆台、球。其中棱柱、圆柱统称为柱体,棱锥、圆锥统称为锥体,棱台、圆台统称为台体,所以简单空间几何体概括分类为:柱体、锥体、台体和球体。
二、简单组合体
1.简单组合体的定义
由简单几何体组合而成的几何体叫作简单组合体.
2.简单组合体的两种基本形式
(1)由简单几何体拼接而成,如课本P103 (1)(2);
(2)由简单几何体截去或挖去一部分而成,如课本P103 (3)(4)。
四、典例分析、举一反三
题型一 旋转体的结构特点
例1 给出下列说法:(1)圆柱的底面是圆面;(2)经过圆柱任意两条母线的截面是一个矩形面;(3)圆台的任意两条母线的延长线可能相交,也可能不相交;(4)夹在圆柱的两个截面间的几何体还是一
个旋转体.其中说法正确的是________.
4547870199390【答案】(1)(2).
【解析】解析 (1)正确,圆柱的底面是圆面.
(2)正确,如图所示,经过圆柱任意两条母线的截面是一个矩形面;
(3)不正确,圆台的母线延长相交于一点;
(4)不正确,圆柱夹在两个平行于底面的截面间的几何体才是旋转体.
解题技巧(判断旋转体结构特点的注意事项)
1.判断简单旋转体结构特征的方法
(1)明确由哪个平面图形旋转而成.
(2)明确旋转轴是哪条直线.
2.简单旋转体的轴截面及其应用
(1)简单旋转体的轴截面中有底面半径、母线、高等体现简单旋转体结构特征的关键量.
(2)在轴截面中解决简单旋转体问题体现了化空间图形为平面图形的转化思想.
跟踪训练一
1、判断下列各命题是否正确.
(1)一直角梯形绕下底所在直线旋转一周,所形成的曲面围成的几何体是圆台;
(2)圆锥、圆台中过轴的截面是轴截面,圆锥的轴截面是等腰三角形,圆台的轴截面是等腰梯形;
(3)到定点的距离等于定长的点的集合是球.
【答案】(1)错误.(2)正确.(3)错误.
【解析】(1)错误.直角梯形绕下底所在直线旋转一周所形成的几何体是由一个圆柱与一个圆锥组成的简单组合体,如图所示.
(2)正确.
(3)错误.应为球面.
题型二 简单组合体
例2 观察下列几何体的结构特点,完成以下问题:
(1)几何体①是由哪些简单几何体构成的?试画出几何图形,使得旋转该图形180°后得到几何体①.
(2)几何体②的结构特点是什么?试画出几何图形,使得旋转该图形360°得到几何体②.
(3)几何体③是由哪些简单几何体构成的?并说明该几何体的面数、棱数、顶点数.
【答案】 (1)几何体①是由圆锥和圆台组合而成的.图见解析.
(2)几何体②是由一个圆台,从上而下挖去一个圆锥而得到,且圆锥的顶点恰为圆台底面圆的圆心.图见解析.
(3)几何体③是由一个四棱锥与一个四棱柱组合而成,且四棱锥的底面与四棱柱底面相同.该几何体共有9个面、9个顶点、16条棱.
【解析】 (1)几何体①是由圆锥和圆台组合而成的.可旋转如下图(a)180°得到几何体①.
(2)几何体②是由一个圆台,从上而下挖去一个圆锥而得到,且圆锥的顶点恰为圆台底面圆的圆心.
可旋转如图(b)360°得到几何体②.
(3)几何体③是由一个四棱锥与一个四棱柱组合而成,且四棱锥的底面与四棱柱底面相同.
14960603175该几何体共有9个面、9个顶点、16条棱.
解题技巧 (解决组合体问题的注意事项)
1.明确组合体的结构特征,主要弄清它是由哪些简单几何体组成的,必要时也可以指出棱数、面数和顶点数,如几何体③所示的组合体有9个面、9个顶点、16条棱.
2.会识别较复杂的图形是学好立体几何的第一步,因此我们应注意观察周围的物体,然后将它们“拆分”成几个简单的几何体,进而培养我们的空间想象能力和识图能力.
跟踪训练二
1、下列组合体是由哪些几何体组成的?
【答案】(1)由两个几何体组合而成,分别为球、圆柱.
(2)由三个几何体组合而成,分别为圆柱、圆台、圆柱.
(3)由三个几何体组合而成,分别为圆锥、圆柱、圆台..
【解析】(1)由两个几何体组合而成,分别为球、圆柱.
(2)由三个几何体组合而成,分别为圆柱、圆台、圆柱.
(3)由三个几何体组合而成,分别为圆锥、圆柱、圆台.
题型三 旋转体的有关计算
例3 已知球的半径为10 cm,若它的一个截面圆的面积为36π cm2,则球心与截面圆圆心的距离是________ cm.
500507059690【答案】8.
【解析】如图,设截面圆的半径为r,球心与截面圆圆心之间的距离为d,球半径为R.由示意图易构造出一个直角三角形,解该直角三角形即可.
由已知,R=10 cm,由πr2=36π cm2,得r=6 cm,
所以d===8(cm).
4103370300355例4 如图,底面半径为1,高为2的圆柱,在A点有一只蚂蚁,现在这只蚂蚁要围绕圆柱由A点爬到B点,问蚂蚁爬行的最短距离是多少?
【答案】2.
【解析】把圆柱的侧面沿AB剪开,然后展开成为平面图形——矩形,如图所示,连接AB′,则AB′即为蚂蚁爬行的最短距离.
∵AB=A′B′=2,AA′为底面圆的周长,且AA′=2π×1=2π,
∴AB′===2,
∴蚂蚁爬行的最短距离为2.
解题技巧(解决侧面展开图相关问题的解题策略)
解此类题的关键要清楚几何体的侧面展开图是什么样的平面图形,并进行合理的空间想象,且记住以下常见几何体的侧面展开图:
跟踪训练三
如图,圆台侧面的母线AB的长为20 cm,上、下底面的半径分别为5 cm,10 cm,从母线AB的中点M处拉一条绳子绕圆台侧面转到B点,求这条绳子长度的最小值.
【答案】50 cm.
【解析】作出圆台的侧面展开图,如图所示,
由Rt△OPA与Rt△OQB相似,
2071370419101499870527059156703302019812027305得 = ,即 = ,
解得OA=20,所以OB=40.
1366520292100设∠BOB′=α,由弧BB′的长与底面圆Q的周长相等,
得2×10×π=π·OB· ,
解得α=90°.所以在Rt△B′OM中,
B′M2=OB′2+OM2=402+302=502,所以B′M=50.
即所求绳长的最小值为50 cm.
五、课堂小结
让学生总结本节课所学主要知识及解题技巧
六、板书设计
基本几何图形
第2课时 圆柱、圆锥、圆台、球、简单组合体
常见旋转体 例1 例2 例3 例4
圆柱
圆锥
圆台
球
2. 简单组合体
七、作业
课本104页练习,105页习题8.1的剩余题.
本节课作为立体几何的第一节,概念比较多,理解起来需要一定的空间想象力,但有一小部分学生缺乏空间想象能力,所以上课的时候提前准备一些模型会更好,借助模型学生对棱柱、棱锥、棱台结构特征的理解会更加透彻.
第2课时 圆柱、圆锥、圆台、球、简单组合体
立体几何是研究三维空间中物体的形状、大小、位置关系的一门数学学科,而三维空间是人们生存发展的现实空间,学习立体几何对我们更好地认识客观世界,更好地生存与发展具有重要意义。在立体几何初步部分,学生将先从对空间几何体观察入手、认识空间图形;再以长方体为载体,直观认识和理解空间点、线、面的位置关系。本节内容既是义务教育阶段“空间与图形”课程的延续和提高,也是后续研究空间点、线、面位置关系的基础,既巩固了前面所学的内容,又为后面内容的学习做了知识上和方法上的准备,在教材中起着承前启后的作用。
课程目标
1.认识圆柱、圆锥、圆台、球的结构特征.
2.认识柱、锥、台、球及其简单组合体的结构特征,并能运用这些特征描述现实生活中简单物体的结构.
数学学科素养
1.数学抽象:简单组合体概念的理解;
2.逻辑推理:圆柱、圆锥、圆台、球的结构特点;
3.直观想象:判断空间几何体;
4.数学运算:球的相关计算、最短距离等;
5.数学建模:通过平面展开图将空间问题转化为平面问题解决,体现了转化的思想方法.
重点:掌握圆柱、圆锥、圆台、球的结构特征;
难点:旋转体的相关计算.
教学方法:以学生为主体,小组为单位,采用诱思探究式教学,精讲多练。
教学工具:多媒体。
情景导入
上节课学了常见的多面体:棱柱、棱锥、棱台,那么常见的旋转体有哪些?又有什么结构特点?
要求:让学生自由发言,教师不做判断。而是引导学生进一步观察.研探.
二、预习课本,引入新课
阅读课本101-104页,思考并完成以下问题
1、旋转体包含哪些图形?
2、圆柱、圆锥、圆台、球是怎样定义的?又有什么结构特点?
3、什么是简单组合体,特点是什么?
要求:学生独立完成,以小组为单位,组内可商量,最终选出代表回答问题。
三、新知探究
一、常见的旋转体
1、圆柱:
定义:以矩形的一边所在的直线为旋转轴,其余三边旋转形成的面所围成的旋转体。
旋转轴叫做圆柱的轴;垂直于轴的边旋转而成的圆面叫做圆柱的底面;平行于轴的边旋转而成曲面叫做圆柱的侧面;无论旋转到什么位置,不垂直于轴的边都叫做圆柱侧面的母线。
圆柱用表示它的轴的字母表示,如圆柱O’O。
2、圆锥:以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的面围成的旋转体。圆锥也有轴、底面、侧面和母线。
圆锥也用表示它的轴的字母表示,如圆锥SO。
3、圆台:用平行于圆锥底面的平面去截圆锥,底面和截面之间的部分叫做圆台。圆台也有轴、底面、侧面、母线。
圆台也用表示它的轴的字母表示,如圆台O’O。
4、球:以半圆的直径所在的直线为旋转轴,半圆面旋转一周形成的旋转体叫做球体。
半圆的圆心叫做球心,半圆的半径叫做球的半径,半圆的直径叫做球的直径,
球常用球心字母O表示,如球O。
小结:常见空间几何体有棱柱、棱锥、棱台、圆柱、圆锥、圆台、球。其中棱柱、圆柱统称为柱体,棱锥、圆锥统称为锥体,棱台、圆台统称为台体,所以简单空间几何体概括分类为:柱体、锥体、台体和球体。
二、简单组合体
1.简单组合体的定义
由简单几何体组合而成的几何体叫作简单组合体.
2.简单组合体的两种基本形式
(1)由简单几何体拼接而成,如课本P103 (1)(2);
(2)由简单几何体截去或挖去一部分而成,如课本P103 (3)(4)。
四、典例分析、举一反三
题型一 旋转体的结构特点
例1 给出下列说法:(1)圆柱的底面是圆面;(2)经过圆柱任意两条母线的截面是一个矩形面;(3)圆台的任意两条母线的延长线可能相交,也可能不相交;(4)夹在圆柱的两个截面间的几何体还是一
个旋转体.其中说法正确的是________.
4547870199390【答案】(1)(2).
【解析】解析 (1)正确,圆柱的底面是圆面.
(2)正确,如图所示,经过圆柱任意两条母线的截面是一个矩形面;
(3)不正确,圆台的母线延长相交于一点;
(4)不正确,圆柱夹在两个平行于底面的截面间的几何体才是旋转体.
解题技巧(判断旋转体结构特点的注意事项)
1.判断简单旋转体结构特征的方法
(1)明确由哪个平面图形旋转而成.
(2)明确旋转轴是哪条直线.
2.简单旋转体的轴截面及其应用
(1)简单旋转体的轴截面中有底面半径、母线、高等体现简单旋转体结构特征的关键量.
(2)在轴截面中解决简单旋转体问题体现了化空间图形为平面图形的转化思想.
跟踪训练一
1、判断下列各命题是否正确.
(1)一直角梯形绕下底所在直线旋转一周,所形成的曲面围成的几何体是圆台;
(2)圆锥、圆台中过轴的截面是轴截面,圆锥的轴截面是等腰三角形,圆台的轴截面是等腰梯形;
(3)到定点的距离等于定长的点的集合是球.
【答案】(1)错误.(2)正确.(3)错误.
【解析】(1)错误.直角梯形绕下底所在直线旋转一周所形成的几何体是由一个圆柱与一个圆锥组成的简单组合体,如图所示.
(2)正确.
(3)错误.应为球面.
题型二 简单组合体
例2 观察下列几何体的结构特点,完成以下问题:
(1)几何体①是由哪些简单几何体构成的?试画出几何图形,使得旋转该图形180°后得到几何体①.
(2)几何体②的结构特点是什么?试画出几何图形,使得旋转该图形360°得到几何体②.
(3)几何体③是由哪些简单几何体构成的?并说明该几何体的面数、棱数、顶点数.
【答案】 (1)几何体①是由圆锥和圆台组合而成的.图见解析.
(2)几何体②是由一个圆台,从上而下挖去一个圆锥而得到,且圆锥的顶点恰为圆台底面圆的圆心.图见解析.
(3)几何体③是由一个四棱锥与一个四棱柱组合而成,且四棱锥的底面与四棱柱底面相同.该几何体共有9个面、9个顶点、16条棱.
【解析】 (1)几何体①是由圆锥和圆台组合而成的.可旋转如下图(a)180°得到几何体①.
(2)几何体②是由一个圆台,从上而下挖去一个圆锥而得到,且圆锥的顶点恰为圆台底面圆的圆心.
可旋转如图(b)360°得到几何体②.
(3)几何体③是由一个四棱锥与一个四棱柱组合而成,且四棱锥的底面与四棱柱底面相同.
14960603175该几何体共有9个面、9个顶点、16条棱.
解题技巧 (解决组合体问题的注意事项)
1.明确组合体的结构特征,主要弄清它是由哪些简单几何体组成的,必要时也可以指出棱数、面数和顶点数,如几何体③所示的组合体有9个面、9个顶点、16条棱.
2.会识别较复杂的图形是学好立体几何的第一步,因此我们应注意观察周围的物体,然后将它们“拆分”成几个简单的几何体,进而培养我们的空间想象能力和识图能力.
跟踪训练二
1、下列组合体是由哪些几何体组成的?
【答案】(1)由两个几何体组合而成,分别为球、圆柱.
(2)由三个几何体组合而成,分别为圆柱、圆台、圆柱.
(3)由三个几何体组合而成,分别为圆锥、圆柱、圆台..
【解析】(1)由两个几何体组合而成,分别为球、圆柱.
(2)由三个几何体组合而成,分别为圆柱、圆台、圆柱.
(3)由三个几何体组合而成,分别为圆锥、圆柱、圆台.
题型三 旋转体的有关计算
例3 已知球的半径为10 cm,若它的一个截面圆的面积为36π cm2,则球心与截面圆圆心的距离是________ cm.
500507059690【答案】8.
【解析】如图,设截面圆的半径为r,球心与截面圆圆心之间的距离为d,球半径为R.由示意图易构造出一个直角三角形,解该直角三角形即可.
由已知,R=10 cm,由πr2=36π cm2,得r=6 cm,
所以d===8(cm).
4103370300355例4 如图,底面半径为1,高为2的圆柱,在A点有一只蚂蚁,现在这只蚂蚁要围绕圆柱由A点爬到B点,问蚂蚁爬行的最短距离是多少?
【答案】2.
【解析】把圆柱的侧面沿AB剪开,然后展开成为平面图形——矩形,如图所示,连接AB′,则AB′即为蚂蚁爬行的最短距离.
∵AB=A′B′=2,AA′为底面圆的周长,且AA′=2π×1=2π,
∴AB′===2,
∴蚂蚁爬行的最短距离为2.
解题技巧(解决侧面展开图相关问题的解题策略)
解此类题的关键要清楚几何体的侧面展开图是什么样的平面图形,并进行合理的空间想象,且记住以下常见几何体的侧面展开图:
跟踪训练三
如图,圆台侧面的母线AB的长为20 cm,上、下底面的半径分别为5 cm,10 cm,从母线AB的中点M处拉一条绳子绕圆台侧面转到B点,求这条绳子长度的最小值.
【答案】50 cm.
【解析】作出圆台的侧面展开图,如图所示,
由Rt△OPA与Rt△OQB相似,
2071370419101499870527059156703302019812027305得 = ,即 = ,
解得OA=20,所以OB=40.
1366520292100设∠BOB′=α,由弧BB′的长与底面圆Q的周长相等,
得2×10×π=π·OB· ,
解得α=90°.所以在Rt△B′OM中,
B′M2=OB′2+OM2=402+302=502,所以B′M=50.
即所求绳长的最小值为50 cm.
五、课堂小结
让学生总结本节课所学主要知识及解题技巧
六、板书设计
基本几何图形
第2课时 圆柱、圆锥、圆台、球、简单组合体
常见旋转体 例1 例2 例3 例4
圆柱
圆锥
圆台
球
2. 简单组合体
七、作业
课本104页练习,105页习题8.1的剩余题.
本节课作为立体几何的第一节,概念比较多,理解起来需要一定的空间想象力,但有一小部分学生缺乏空间想象能力,所以上课的时候提前准备一些模型会更好,借助模型学生对棱柱、棱锥、棱台结构特征的理解会更加透彻.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
