九年级下人教版27.2.1 第3课时 两边成比例且夹角相等的两个三角形相似 同步练习(word版含答案)
文档属性
| 名称 | 九年级下人教版27.2.1 第3课时 两边成比例且夹角相等的两个三角形相似 同步练习(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 258.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-22 10:58:49 | ||
图片预览




文档简介
27.2 相似三角形
27.2.1 相似三角形的判定
第3课时
两边成比例且夹角相等的两个三角形相似
1.如图,在△ABC中点D在线段BC上,请添加一条件使△ABC∽△DBA,则下列条件中一定正确的是( )
A.AB2=AC?BD
B.AB2=BC?BD
C.AB?AD=BD?BC
D.AB?AD=AC?BD
2.如图,△ABC中,∠A=60°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,剪下的三角形与△ABC不相似的是( )
A.
B.
C.
D.
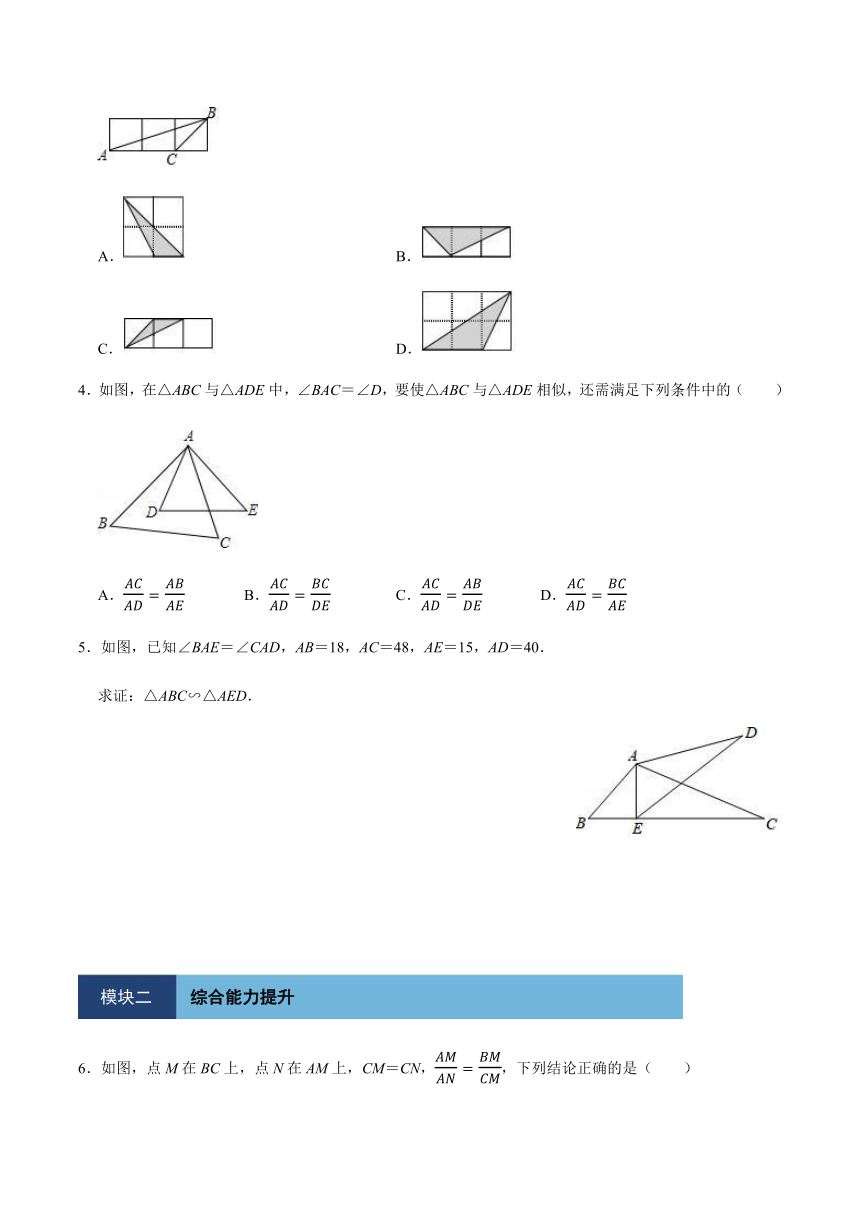
3.如图,△ABC和阴影三角形的顶点都在小正方形的顶点上,则与△ABC相似的阴影三角形为( )
A.
B.
C.
D.
4.如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )
A.
B.
C.
D.
5.如图,已知∠BAE=∠CAD,AB=18,AC=48,AE=15,AD=40.
求证:△ABC∽△AED.
6.如图,点M在BC上,点N在AM上,CM=CN,,下列结论正确的是( )
A.△ABM∽△ACB
B.△ANC∽△AMB
C.△ANC∽△ACM
D.△CMN∽△BCA
7.如图,已知△ABC和△PBD都是正方形网格上的格点三角形(顶点为网格线的交点),要使△ABC∽△PBD,则点P的位置应落在( )
A.点P1上
B.点P2上
C.点P3上
D.点P4上
8.如图,在△ABC中,∠A=90°,点D在边BC上,AB=BD=3,CD=2,点E是边AC上的动点,当CE=
时,以点C、D、E为顶点的三角形与△ABC相似.
9.已知,如图,△ABC中,AB=4,BC=8,D为BC边上一点,BD=2.
(1)求证:△ABD∽△CBA;
(2)作DE∥AB交AC于点E,请再写出另一个与△ABD相似的三角形,并直接写出DE的长.
10.如图,四边形ABCD中,AC、BD相交于点F,点E在BD上,且,则图中有几对相似三角形,并加以证明.
11.如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DFDC,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求FG的长.
12.如图,在Rt△ABC中,∠A=90°,BC=10cm,AC=6cm,在线段BC上,动点P以2cm/s的速度从点B向点C匀速运动;同时在线段CA上,点Q以acm/s的速度从点C向点A匀速运动,当点P到达点C(或点Q到达点A)时,两点运动停止,在运动过程中.
(1)当点P运动s时,△CPQ与△ABC第一次相似,求点Q的速度a;
(2)当△CPQ与△ABC第二次相似时,求点P总共运动了多少秒?
参考答案与试题解析
1.解:若添加AB2=AC?BD,不能判定△ABC∽△DBA;故A选项不符合题意,
若添加AB2=BC?BD,能判定△ABC∽△DBA;
理由:∵AB2=BC?BD,
∴,
又∵∠ABD=∠CBA,
∴△ABC∽△DBA.
故B选项符合题意,
若添加AB?AD=BD?BC,不能判定△ABC∽△DBA;故C选项不符合题意,
若添加AB?AD=AC?BD,不能判定△ABC∽△DBA.故D选项不符合题意,
故选:B.
2.解:A、两三角形的对应边成比例,但夹角不相等,故两三角形不相似,故本选项符合题意;
B、两三角形对应边成比例且夹角相等,故两三角形相似,故本选项不符合题意;
C、阴影三角形与原三角形有两个角相等,故两三角形相似,故本选项不符合题意;
D、阴影三角形与原三角形有两个角相等,故两三角形相似,故本选项不符合题意;
故选:A.
3.解:观察图象可知只有选项C含有135°角,且两边的比为:1,
故选:C.
4.解:∵∠BAC=∠D,,
∴△ABC∽△ADE.
故选:C.
5.解:∵∠BAE=∠CAD,
∴∠BAE+∠EAC=∠CAD+∠EAC,即∠BAC=∠EAD,
∵AB=18,AC=48,AE=15,AD=40,
∴,
∴△ABC∽△AED.
6.解:∵CM=CN
∴∠CNM=∠CMN
∵∠CNA=∠CMN+∠MCN,∠AMB=∠CNM+∠MCN
∴∠CNA=∠AMB
∵AM:AN=BM:CM
∴AM:AN=BM:CN
∴△ANC∽△AMB
故选:B.
7.解:由图知:∠BAC是钝角,又△ABC∽△PBD,
则∠BPD一定是钝角,∠BPD=∠BAC,
又BA=2,AC=2,
∴BA:AC=1:,
∴BP:PD=1:或BP:PD:1,
只有P2符合这样的要求,故P点应该在P2.
故选:B.
8.解:∵在△ABC中,∠A=90°,AB=BD=3,CD=2,
∴AC,
∵当,∠C=∠C,
∴△ADE∽△ABC,
∴CE,
∵,∠C=∠C,
∴△ADE∽△ABC,
∴CE,
故答案为:或.
9.(1)证明:∵AB=4,BC=8,BD=2,
∴.
∵∠ABD=∠CBA,
△ABD∽△CBA,
(2)作DE∥AB交AC于点E,如图所示,△ABD∽△CDE;
,
即,
解得:DE=3.
10.解:图中有4对相似三角形,
∵,
∴△ABC∽△AED,
∴∠BAC=∠EAD,
∴∠BAE=∠CAD;
∵,
∴.
∵∠BAE=∠CAD,
∴△ABE∽△ACD,
∵△ABC∽△AED,
∴∠ADE=∠ACB,
∵∠AFD=∠BFC,
∴△DAF∽△CBF,
∵△ABE∽△ACD,
∴∠ABF=∠ACD,
∵∠AFB=∠DFC,
∴△ABF∽△DCF.
11.(1)证明:∵四边形ABCD为正方形,
∴AD=AB=DC=BC,∠A=∠D=90°,
∵AE=ED,
∴,
∵DFDC,
∴,
∴,
∴△ABE∽△DEF;
(2)∵四边形ABCD为正方形,
∴ED∥BG,
∴△DEF∽△CGF,
∴,
又∵DFDC,正方形的边长为4,
∴DF=1,ED=2,
∴CF=3,CG=6,
∴GF3.
12.解:(1)如图1,BP2,
∵∠QCP=∠ACB,
∴当,△CPQ∽△CBA,即,解得a=1,
∴点Q的速度a为1cm/s;
(2)如图2,设点P总共运动了t秒,
∵∠QCP=∠ACB,
∴当,△CPQ∽△CAB,即,解得t,
∴点P总共运动了秒.
27.2.1 相似三角形的判定
第3课时
两边成比例且夹角相等的两个三角形相似
1.如图,在△ABC中点D在线段BC上,请添加一条件使△ABC∽△DBA,则下列条件中一定正确的是( )
A.AB2=AC?BD
B.AB2=BC?BD
C.AB?AD=BD?BC
D.AB?AD=AC?BD
2.如图,△ABC中,∠A=60°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,剪下的三角形与△ABC不相似的是( )
A.
B.
C.
D.
3.如图,△ABC和阴影三角形的顶点都在小正方形的顶点上,则与△ABC相似的阴影三角形为( )
A.
B.
C.
D.
4.如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )
A.
B.
C.
D.
5.如图,已知∠BAE=∠CAD,AB=18,AC=48,AE=15,AD=40.
求证:△ABC∽△AED.
6.如图,点M在BC上,点N在AM上,CM=CN,,下列结论正确的是( )
A.△ABM∽△ACB
B.△ANC∽△AMB
C.△ANC∽△ACM
D.△CMN∽△BCA
7.如图,已知△ABC和△PBD都是正方形网格上的格点三角形(顶点为网格线的交点),要使△ABC∽△PBD,则点P的位置应落在( )
A.点P1上
B.点P2上
C.点P3上
D.点P4上
8.如图,在△ABC中,∠A=90°,点D在边BC上,AB=BD=3,CD=2,点E是边AC上的动点,当CE=
时,以点C、D、E为顶点的三角形与△ABC相似.
9.已知,如图,△ABC中,AB=4,BC=8,D为BC边上一点,BD=2.
(1)求证:△ABD∽△CBA;
(2)作DE∥AB交AC于点E,请再写出另一个与△ABD相似的三角形,并直接写出DE的长.
10.如图,四边形ABCD中,AC、BD相交于点F,点E在BD上,且,则图中有几对相似三角形,并加以证明.
11.如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DFDC,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求FG的长.
12.如图,在Rt△ABC中,∠A=90°,BC=10cm,AC=6cm,在线段BC上,动点P以2cm/s的速度从点B向点C匀速运动;同时在线段CA上,点Q以acm/s的速度从点C向点A匀速运动,当点P到达点C(或点Q到达点A)时,两点运动停止,在运动过程中.
(1)当点P运动s时,△CPQ与△ABC第一次相似,求点Q的速度a;
(2)当△CPQ与△ABC第二次相似时,求点P总共运动了多少秒?
参考答案与试题解析
1.解:若添加AB2=AC?BD,不能判定△ABC∽△DBA;故A选项不符合题意,
若添加AB2=BC?BD,能判定△ABC∽△DBA;
理由:∵AB2=BC?BD,
∴,
又∵∠ABD=∠CBA,
∴△ABC∽△DBA.
故B选项符合题意,
若添加AB?AD=BD?BC,不能判定△ABC∽△DBA;故C选项不符合题意,
若添加AB?AD=AC?BD,不能判定△ABC∽△DBA.故D选项不符合题意,
故选:B.
2.解:A、两三角形的对应边成比例,但夹角不相等,故两三角形不相似,故本选项符合题意;
B、两三角形对应边成比例且夹角相等,故两三角形相似,故本选项不符合题意;
C、阴影三角形与原三角形有两个角相等,故两三角形相似,故本选项不符合题意;
D、阴影三角形与原三角形有两个角相等,故两三角形相似,故本选项不符合题意;
故选:A.
3.解:观察图象可知只有选项C含有135°角,且两边的比为:1,
故选:C.
4.解:∵∠BAC=∠D,,
∴△ABC∽△ADE.
故选:C.
5.解:∵∠BAE=∠CAD,
∴∠BAE+∠EAC=∠CAD+∠EAC,即∠BAC=∠EAD,
∵AB=18,AC=48,AE=15,AD=40,
∴,
∴△ABC∽△AED.
6.解:∵CM=CN
∴∠CNM=∠CMN
∵∠CNA=∠CMN+∠MCN,∠AMB=∠CNM+∠MCN
∴∠CNA=∠AMB
∵AM:AN=BM:CM
∴AM:AN=BM:CN
∴△ANC∽△AMB
故选:B.
7.解:由图知:∠BAC是钝角,又△ABC∽△PBD,
则∠BPD一定是钝角,∠BPD=∠BAC,
又BA=2,AC=2,
∴BA:AC=1:,
∴BP:PD=1:或BP:PD:1,
只有P2符合这样的要求,故P点应该在P2.
故选:B.
8.解:∵在△ABC中,∠A=90°,AB=BD=3,CD=2,
∴AC,
∵当,∠C=∠C,
∴△ADE∽△ABC,
∴CE,
∵,∠C=∠C,
∴△ADE∽△ABC,
∴CE,
故答案为:或.
9.(1)证明:∵AB=4,BC=8,BD=2,
∴.
∵∠ABD=∠CBA,
△ABD∽△CBA,
(2)作DE∥AB交AC于点E,如图所示,△ABD∽△CDE;
,
即,
解得:DE=3.
10.解:图中有4对相似三角形,
∵,
∴△ABC∽△AED,
∴∠BAC=∠EAD,
∴∠BAE=∠CAD;
∵,
∴.
∵∠BAE=∠CAD,
∴△ABE∽△ACD,
∵△ABC∽△AED,
∴∠ADE=∠ACB,
∵∠AFD=∠BFC,
∴△DAF∽△CBF,
∵△ABE∽△ACD,
∴∠ABF=∠ACD,
∵∠AFB=∠DFC,
∴△ABF∽△DCF.
11.(1)证明:∵四边形ABCD为正方形,
∴AD=AB=DC=BC,∠A=∠D=90°,
∵AE=ED,
∴,
∵DFDC,
∴,
∴,
∴△ABE∽△DEF;
(2)∵四边形ABCD为正方形,
∴ED∥BG,
∴△DEF∽△CGF,
∴,
又∵DFDC,正方形的边长为4,
∴DF=1,ED=2,
∴CF=3,CG=6,
∴GF3.
12.解:(1)如图1,BP2,
∵∠QCP=∠ACB,
∴当,△CPQ∽△CBA,即,解得a=1,
∴点Q的速度a为1cm/s;
(2)如图2,设点P总共运动了t秒,
∵∠QCP=∠ACB,
∴当,△CPQ∽△CAB,即,解得t,
∴点P总共运动了秒.
