2020-2021学年人教版九年级数学下册27.2.1 第4课时 两角分别相等的两个三角形相似同步练习(word版含答案)
文档属性
| 名称 | 2020-2021学年人教版九年级数学下册27.2.1 第4课时 两角分别相等的两个三角形相似同步练习(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 234.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-22 11:59:11 | ||
图片预览



文档简介
27.2 相似三角形
27.2.1 相似三角形的判定
第4课时
两角分别相等的两个三角形相似
1.下列各组条件,不能判定△ABC与△A′B′C′相似的是( )
A.∠A=∠A′∠B=∠B′
B.∠C=∠C′=90°,∠A=12°,∠B′=78°
C.∠A=∠B,∠B′=∠A′
D.∠A+∠B=∠A′+∠B′,∠A﹣∠B=∠A′﹣∠B′
2.如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )
A.4
B.6
C.4
D.4
3.已知:如图,∠1=∠2=∠3,求证:△ABC∽△ADE.
4.如图,在△ABC中,∠ABC=80°,∠BAC=40°,AB的垂直平分线分别与AC,AB相交于点D,E,连接BD,求证:△ABC∽△BDC.
5.在Rt△ABC和Rt△DEF中,∠C=∠F=90°,下列各组的条件不能判定这两个三角形相似的是( )
A.∠A=65°,∠D=25°
B.AC=3,BC=4,DF=6,DE=8
C.AC=9,BC=12,DF=12,EF=16
D.AB=10,AC=8,DE=35,EF=21
6.如图,在Rt△ACB中,∠ACB=90°,CD⊥AB于D,则图中相似的三角形有( )
A.4对
B.3对
C.2对
D.1对
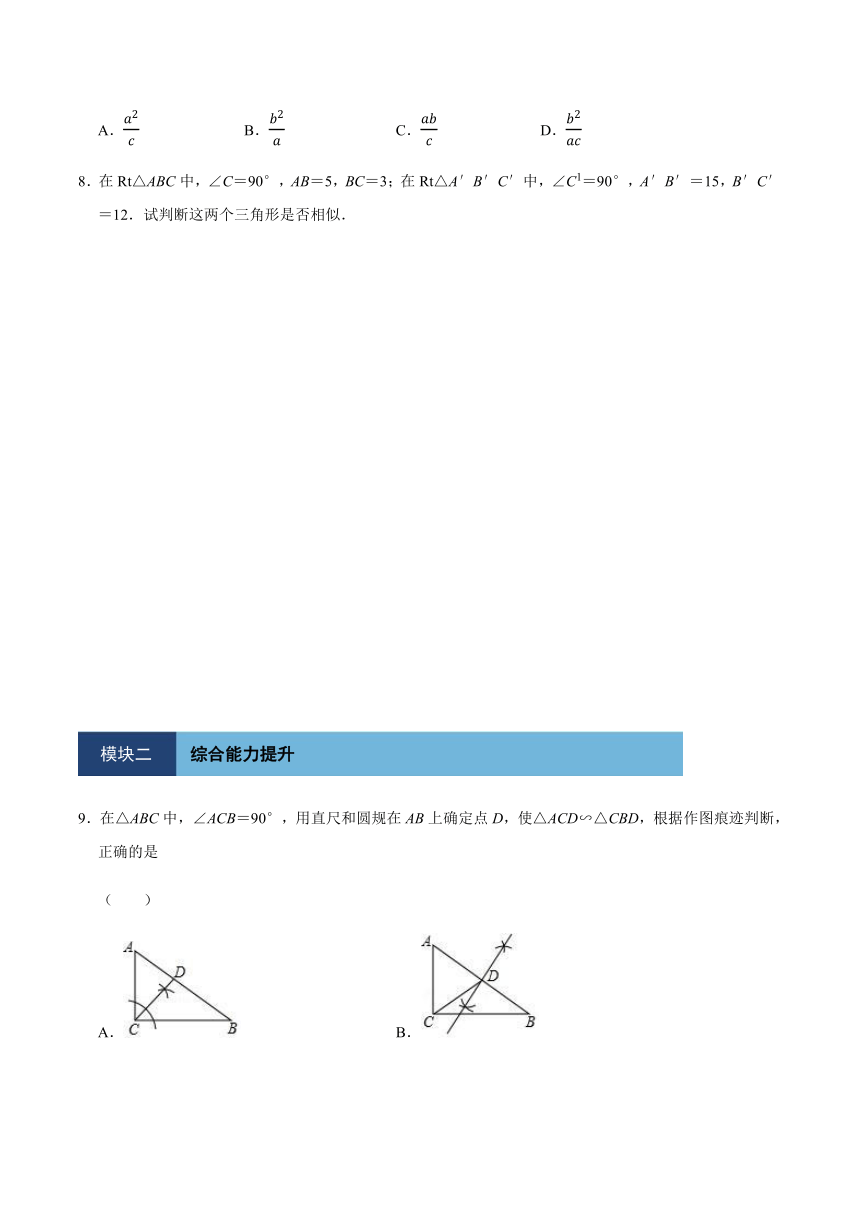
7.如图,已知△ABC和△ADC均为直角三角形,点B,D位于AC的两侧,∠ACB=∠ADC=90°,BC=a,AC=b,AB=c,要使△ACD∽△ABC,CD可以等于( )
A.
B.
C.
D.
8.在Rt△ABC中,∠C=90°,AB=5,BC=3;在Rt△A′B′C′中,∠C1=90°,A′B′=15,B′C′=12.试判断这两个三角形是否相似.
9.在△ABC中,∠ACB=90°,用直尺和圆规在AB上确定点D,使△ACD∽△CBD,根据作图痕迹判断,正确的是
( )
A.
B.
C.
D.
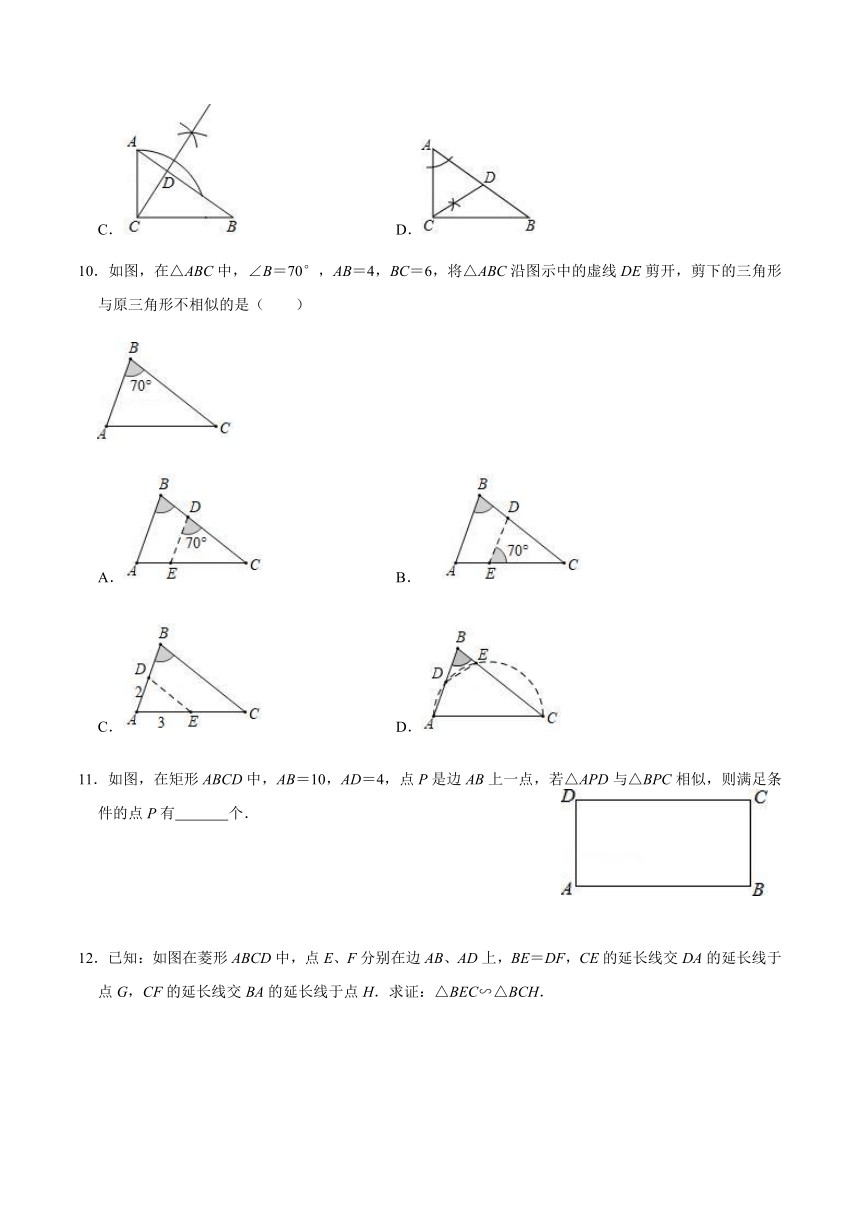
10.如图,在△ABC中,∠B=70°,AB=4,BC=6,将△ABC沿图示中的虚线DE剪开,剪下的三角形与原三角形不相似的是( )
A.
B.
C.
D.
11.如图,在矩形ABCD中,AB=10,AD=4,点P是边AB上一点,若△APD与△BPC相似,则满足条件的点P有
个.
12.已知:如图在菱形ABCD中,点E、F分别在边AB、AD上,BE=DF,CE的延长线交DA的延长线于点G,CF的延长线交BA的延长线于点H.求证:△BEC∽△BCH.
13.正方形ABCD边长为4,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直,
(1)证明:Rt△ABM∽Rt△MCN;
(2)当M点运动到什么位置时Rt△ABM∽Rt△AMN,并请说明理由.
参考答案与试题解析
1.解:A、若∠A=∠A′∠B=∠B′,则可判断△ABC∽△A′B′C′;
B、∠C=∠C′=90°,∠A=12°,∠B′=78°,则∠A′=12°,所以∠A=∠A′,∠C=∠C′,则可判断△ABC∽△A′B′C′;
C、若∠A=∠B,∠B′=∠A′,则△ABC和△A′B′C′都是等腰三角形,而等腰三角形不一定相似,即不能判定△ABC与△A′B′C′相似;
D、若∠A+∠B=∠A′+∠B′,∠A﹣∠B=∠A′﹣∠B′,则∠A=∠A′∠B=∠B′,则可判断△ABC∽△A′B′C′.
故选:C.
2.解:∵BC=8,
∴CD=4,
在△CBA和△CAD中,
∵∠B=∠DAC,∠C=∠C,
∴△CBA∽△CAD,
∴,
∴AC2=CD?BC=4×8=32,
∴AC=4;
故选:C.
3.证明:∵∠ADC=∠2+∠ADE=∠B+∠1,∠1=∠2,
∴∠ADE=∠B,
∵∠1=∠3,
∴∠BAC=∠DAE,
∴△BAC∽△DAE.
4.证明:
∵DE是AB的垂直平分线,
∴AD=BD.
∵∠BAC=40°,
∴∠ABD=40°,
∵∠ABC=80°,
∴∠DBC=40°,
∴∠DBC=∠BAC,
∵∠C=∠C,
∴△ABC∽△BDC.
5.解:A、相似:∵∠A=65°,∴∠B=90°﹣65°=25°,∵∠D=25°,∴∠B=∠D,又∵∠C=∠F,∴△ABC∽△DEF;
B、相似:∵AC=3,BC=4,DF=6,EF=8,∴,则,又∵∠C=∠F,∴△ABC∽△DEF;
C、相似∵AC=9,BC=12,DF=12,EF=16,∴,则,又∵∠C=∠F,∴△ABC∽△DEF;
D、∵AB=10,BC=8,DE=35,EF=21,∴,∴△ABC和△DEF不相似;
故选:D.
6.解:∵CD⊥AB,
∴∠3=∠4=90°,
∴∠2+∠A=90°,∠1+∠B=90°.
∵∠ACB=90°,
∴∠1+∠2=90°,∠ACB=∠3=∠4.
∴∠1=∠A,∠2=∠B.
∴△ADC∽△CDB,△CDB∽△ACB,△ADC∽△ACB.
∴图中相似的三角形有3对.
故选:B.
7.解:∵△ACD∽△ABC,
∴,
∵BC=a,AC=b,AB=c,
∴,
则DC.
故选:C.
8.解:相似,证明如下:
∵∠C=90°,AB=5,BC=3,
∴AC=4,
∴,,
∴,且∠C=∠C′,
∴△ABC∽△A′B′C′.
9.解:当CD是AB的垂线时,△ACD∽△CBD.
∵CD⊥AB,
∴∠CDA=∠BDC=90°,
∵∠ACB=90°,
∴∠A+∠ACD=∠ACD+∠BCD=90°,
∴∠A=∠BCD,
∴△ACD∽△CBD.
根据作图痕迹可知,
A选项中,CD是∠ACB的角平分线,不符合题意;
B选项中,CD不与AB垂直,不符合题意;
C选项中,CD是AB的垂线,符合题意;
D选项中,CD不与AB垂直,不符合题意;
故选:C.
10.解:A、剪下的三角形与原三角形有两个角相等,故两三角形相似,不符合题意;
B、剪下的三角形与原三角形有两个角相等,故两三角形相似,不符合题意;
C、两三角形的对应边不成比例,故两三角形不相似,符合题意.
D、可得∠BDE=∠ACB,∠B=∠B,剪下的三角形与原三角形有两个角相等,故两三角形相似,不符合题意.
故选:C.
11.解:设AP为x,
∵AB=10,
∴PB=10﹣x,
①AD和PB是对应边时,
∵△APD与△BPC相似,
∴,
即,
整理得,x2﹣10x+16=0,
解得x1=2,x2=8,
②AD和BC是对应边时,
∵△APD与△BPC相似,
∴,
即,
解得x=5,
所以,当AP=2、5、8时,△APD与△BPC相似,
满足条件的点P有3个.
故答案为:3.
12.证明:∵四边形ABCD是菱形,
∴CD=CB,∠D=∠B,
∵DF=BE,
∴△CDF≌△CBE(SAS),
∴∠DCF=∠BCE,
∵CD∥BH,
∴∠H=∠DCF,
∴∠H=∠BCE,
∵∠B=∠B,
∴△BEC∽△BCH.
13.(1)证明:∵四边形ABCD为正方形,
∴∠B=∠C=90°,
∵AM⊥MN,
∴∠AMN=90°,
∴∠AMB+∠NMC=90°,
而∠AMB+∠MAB=90°,
∴∠MBA=∠NMC,
∴Rt△ABM∽Rt△MCN;
(2)解:当M点运动到BC为中点位置时,Rt△ABM∽Rt△AMN.
理由如下:,
∵四边形ABCD为正方形,
∴AB=BC=4,BM=MC=2,
∴AM=2,
∵Rt△ABM∽Rt△MCN,
∴2,
∴MNAM,
∵,,
∴,
而∠ABM=∠AMN=90°,
∴Rt△ABM∽Rt△AMN.
27.2.1 相似三角形的判定
第4课时
两角分别相等的两个三角形相似
1.下列各组条件,不能判定△ABC与△A′B′C′相似的是( )
A.∠A=∠A′∠B=∠B′
B.∠C=∠C′=90°,∠A=12°,∠B′=78°
C.∠A=∠B,∠B′=∠A′
D.∠A+∠B=∠A′+∠B′,∠A﹣∠B=∠A′﹣∠B′
2.如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )
A.4
B.6
C.4
D.4
3.已知:如图,∠1=∠2=∠3,求证:△ABC∽△ADE.
4.如图,在△ABC中,∠ABC=80°,∠BAC=40°,AB的垂直平分线分别与AC,AB相交于点D,E,连接BD,求证:△ABC∽△BDC.
5.在Rt△ABC和Rt△DEF中,∠C=∠F=90°,下列各组的条件不能判定这两个三角形相似的是( )
A.∠A=65°,∠D=25°
B.AC=3,BC=4,DF=6,DE=8
C.AC=9,BC=12,DF=12,EF=16
D.AB=10,AC=8,DE=35,EF=21
6.如图,在Rt△ACB中,∠ACB=90°,CD⊥AB于D,则图中相似的三角形有( )
A.4对
B.3对
C.2对
D.1对
7.如图,已知△ABC和△ADC均为直角三角形,点B,D位于AC的两侧,∠ACB=∠ADC=90°,BC=a,AC=b,AB=c,要使△ACD∽△ABC,CD可以等于( )
A.
B.
C.
D.
8.在Rt△ABC中,∠C=90°,AB=5,BC=3;在Rt△A′B′C′中,∠C1=90°,A′B′=15,B′C′=12.试判断这两个三角形是否相似.
9.在△ABC中,∠ACB=90°,用直尺和圆规在AB上确定点D,使△ACD∽△CBD,根据作图痕迹判断,正确的是
( )
A.
B.
C.
D.
10.如图,在△ABC中,∠B=70°,AB=4,BC=6,将△ABC沿图示中的虚线DE剪开,剪下的三角形与原三角形不相似的是( )
A.
B.
C.
D.
11.如图,在矩形ABCD中,AB=10,AD=4,点P是边AB上一点,若△APD与△BPC相似,则满足条件的点P有
个.
12.已知:如图在菱形ABCD中,点E、F分别在边AB、AD上,BE=DF,CE的延长线交DA的延长线于点G,CF的延长线交BA的延长线于点H.求证:△BEC∽△BCH.
13.正方形ABCD边长为4,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直,
(1)证明:Rt△ABM∽Rt△MCN;
(2)当M点运动到什么位置时Rt△ABM∽Rt△AMN,并请说明理由.
参考答案与试题解析
1.解:A、若∠A=∠A′∠B=∠B′,则可判断△ABC∽△A′B′C′;
B、∠C=∠C′=90°,∠A=12°,∠B′=78°,则∠A′=12°,所以∠A=∠A′,∠C=∠C′,则可判断△ABC∽△A′B′C′;
C、若∠A=∠B,∠B′=∠A′,则△ABC和△A′B′C′都是等腰三角形,而等腰三角形不一定相似,即不能判定△ABC与△A′B′C′相似;
D、若∠A+∠B=∠A′+∠B′,∠A﹣∠B=∠A′﹣∠B′,则∠A=∠A′∠B=∠B′,则可判断△ABC∽△A′B′C′.
故选:C.
2.解:∵BC=8,
∴CD=4,
在△CBA和△CAD中,
∵∠B=∠DAC,∠C=∠C,
∴△CBA∽△CAD,
∴,
∴AC2=CD?BC=4×8=32,
∴AC=4;
故选:C.
3.证明:∵∠ADC=∠2+∠ADE=∠B+∠1,∠1=∠2,
∴∠ADE=∠B,
∵∠1=∠3,
∴∠BAC=∠DAE,
∴△BAC∽△DAE.
4.证明:
∵DE是AB的垂直平分线,
∴AD=BD.
∵∠BAC=40°,
∴∠ABD=40°,
∵∠ABC=80°,
∴∠DBC=40°,
∴∠DBC=∠BAC,
∵∠C=∠C,
∴△ABC∽△BDC.
5.解:A、相似:∵∠A=65°,∴∠B=90°﹣65°=25°,∵∠D=25°,∴∠B=∠D,又∵∠C=∠F,∴△ABC∽△DEF;
B、相似:∵AC=3,BC=4,DF=6,EF=8,∴,则,又∵∠C=∠F,∴△ABC∽△DEF;
C、相似∵AC=9,BC=12,DF=12,EF=16,∴,则,又∵∠C=∠F,∴△ABC∽△DEF;
D、∵AB=10,BC=8,DE=35,EF=21,∴,∴△ABC和△DEF不相似;
故选:D.
6.解:∵CD⊥AB,
∴∠3=∠4=90°,
∴∠2+∠A=90°,∠1+∠B=90°.
∵∠ACB=90°,
∴∠1+∠2=90°,∠ACB=∠3=∠4.
∴∠1=∠A,∠2=∠B.
∴△ADC∽△CDB,△CDB∽△ACB,△ADC∽△ACB.
∴图中相似的三角形有3对.
故选:B.
7.解:∵△ACD∽△ABC,
∴,
∵BC=a,AC=b,AB=c,
∴,
则DC.
故选:C.
8.解:相似,证明如下:
∵∠C=90°,AB=5,BC=3,
∴AC=4,
∴,,
∴,且∠C=∠C′,
∴△ABC∽△A′B′C′.
9.解:当CD是AB的垂线时,△ACD∽△CBD.
∵CD⊥AB,
∴∠CDA=∠BDC=90°,
∵∠ACB=90°,
∴∠A+∠ACD=∠ACD+∠BCD=90°,
∴∠A=∠BCD,
∴△ACD∽△CBD.
根据作图痕迹可知,
A选项中,CD是∠ACB的角平分线,不符合题意;
B选项中,CD不与AB垂直,不符合题意;
C选项中,CD是AB的垂线,符合题意;
D选项中,CD不与AB垂直,不符合题意;
故选:C.
10.解:A、剪下的三角形与原三角形有两个角相等,故两三角形相似,不符合题意;
B、剪下的三角形与原三角形有两个角相等,故两三角形相似,不符合题意;
C、两三角形的对应边不成比例,故两三角形不相似,符合题意.
D、可得∠BDE=∠ACB,∠B=∠B,剪下的三角形与原三角形有两个角相等,故两三角形相似,不符合题意.
故选:C.
11.解:设AP为x,
∵AB=10,
∴PB=10﹣x,
①AD和PB是对应边时,
∵△APD与△BPC相似,
∴,
即,
整理得,x2﹣10x+16=0,
解得x1=2,x2=8,
②AD和BC是对应边时,
∵△APD与△BPC相似,
∴,
即,
解得x=5,
所以,当AP=2、5、8时,△APD与△BPC相似,
满足条件的点P有3个.
故答案为:3.
12.证明:∵四边形ABCD是菱形,
∴CD=CB,∠D=∠B,
∵DF=BE,
∴△CDF≌△CBE(SAS),
∴∠DCF=∠BCE,
∵CD∥BH,
∴∠H=∠DCF,
∴∠H=∠BCE,
∵∠B=∠B,
∴△BEC∽△BCH.
13.(1)证明:∵四边形ABCD为正方形,
∴∠B=∠C=90°,
∵AM⊥MN,
∴∠AMN=90°,
∴∠AMB+∠NMC=90°,
而∠AMB+∠MAB=90°,
∴∠MBA=∠NMC,
∴Rt△ABM∽Rt△MCN;
(2)解:当M点运动到BC为中点位置时,Rt△ABM∽Rt△AMN.
理由如下:,
∵四边形ABCD为正方形,
∴AB=BC=4,BM=MC=2,
∴AM=2,
∵Rt△ABM∽Rt△MCN,
∴2,
∴MNAM,
∵,,
∴,
而∠ABM=∠AMN=90°,
∴Rt△ABM∽Rt△AMN.
