27.3 第1课时 位似图形-2020-2021学年人教版九年级数学下册同步练习(word版含答案)
文档属性
| 名称 | 27.3 第1课时 位似图形-2020-2021学年人教版九年级数学下册同步练习(word版含答案) | 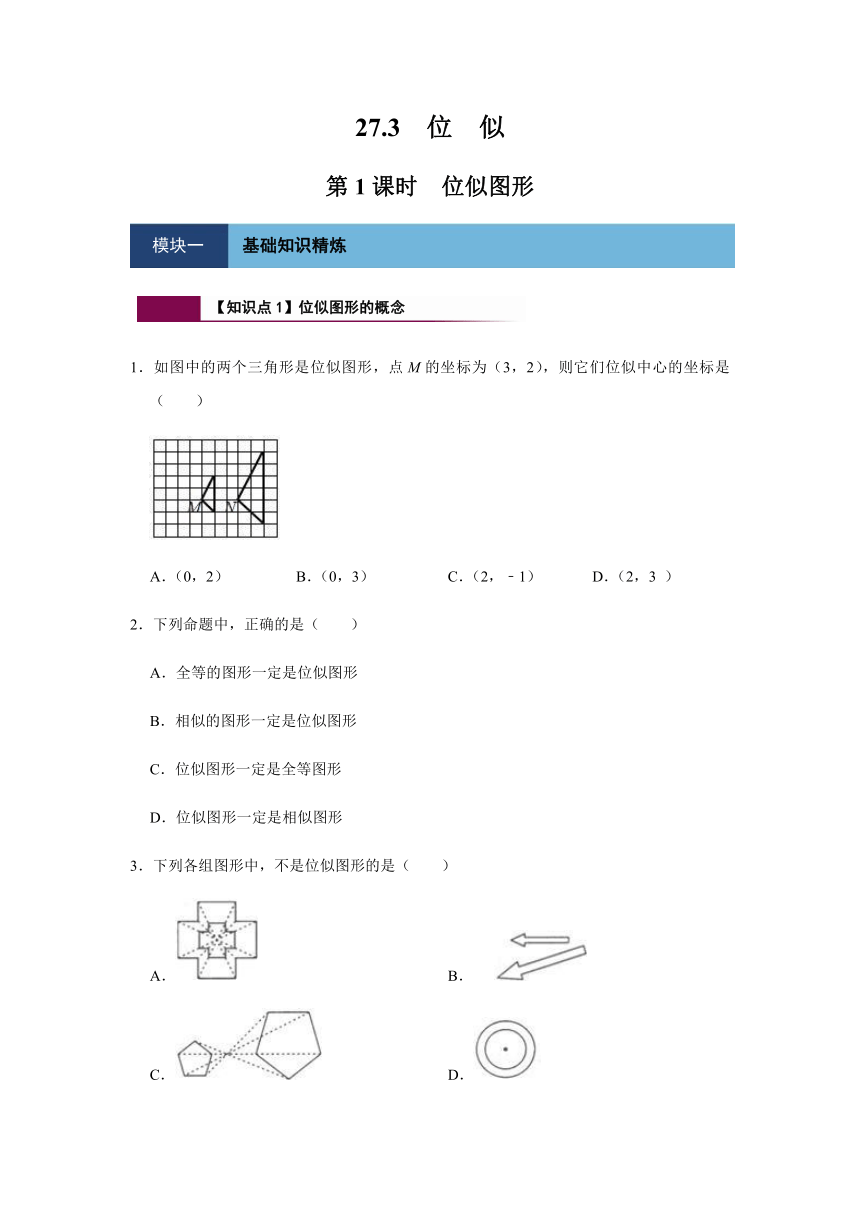 | |
| 格式 | zip | ||
| 文件大小 | 543.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-22 08:26:10 | ||
图片预览




文档简介
27.3 位 似
第1课时 位似图形
1.如图中的两个三角形是位似图形,点M的坐标为(3,2),则它们位似中心的坐标是( )
A.(0,2)
B.(0,3)
C.(2,﹣1)
D.(2,3
)
2.下列命题中,正确的是( )
A.全等的图形一定是位似图形
B.相似的图形一定是位似图形
C.位似图形一定是全等图形
D.位似图形一定是相似图形
3.下列各组图形中,不是位似图形的是( )
A.
B.
C.
D.
4.如图,以点O为位似中心,把△ABC放大为原来的2倍,得到△A′B′C′,以下说法错误的是( )
A.BB′:BO=2:1
B.△ABC∽△A'B'C'
C.AB∥A'B'
D.点C,点O,点C'三点共线
5.如图,△ABC与△DEF位似,点O是位似中心,且OD=2AD,若BC=6,则EF=( )
A.2
B.3
C.4
D.5
6.如图,△ABC与△DEF位似,其位似中心为点O,且D为AO的中点,则△ABC与△DEF的面积比是( )
A.2:1
B.4:1
C.3:1
D.9:1
7.如图,六边形ABCDEF与六边形A1B1C1D1E1F1是位似图形,O为位似中心,ODOD1,则A1B1:AB为( )
A.2:3
B.3:2
C.1:2
D.2:1
8.如图所示,在平面直角坐标系中,有两点A(4,2),B(3,0),以原点为位似中心,A′B′与AB的相似比为,得到线段A′B′.正确的画法是( )
A.
B.
C.
D.
9.如图所示是△ABC位似图形的几种画法,其中正确的是个数是( )
A.1
B.2
C.3
D.4
10.如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点,以格点为顶点,分别按下列要求画三角形.
(1)在图②中,请在网格中画一个与图①△ABC相似的△DEF;
(2)在图③中,以O为位似中心,画一个△A1B1C1,使它与△ABC的位似比为2:1.
11.下列3个图形中是位似图形的有( )
A.0个
B.1个
C.2个
D.3个
12.如图,四边形ABCD与四边形A'B'C'D'位似,点O为位似中心,若OB:OB'=2:3,则四边形ABCD与四边形A'B'C′D'的面积比为( )
A.2:3
B.2:5
C.4:9
D.4:25
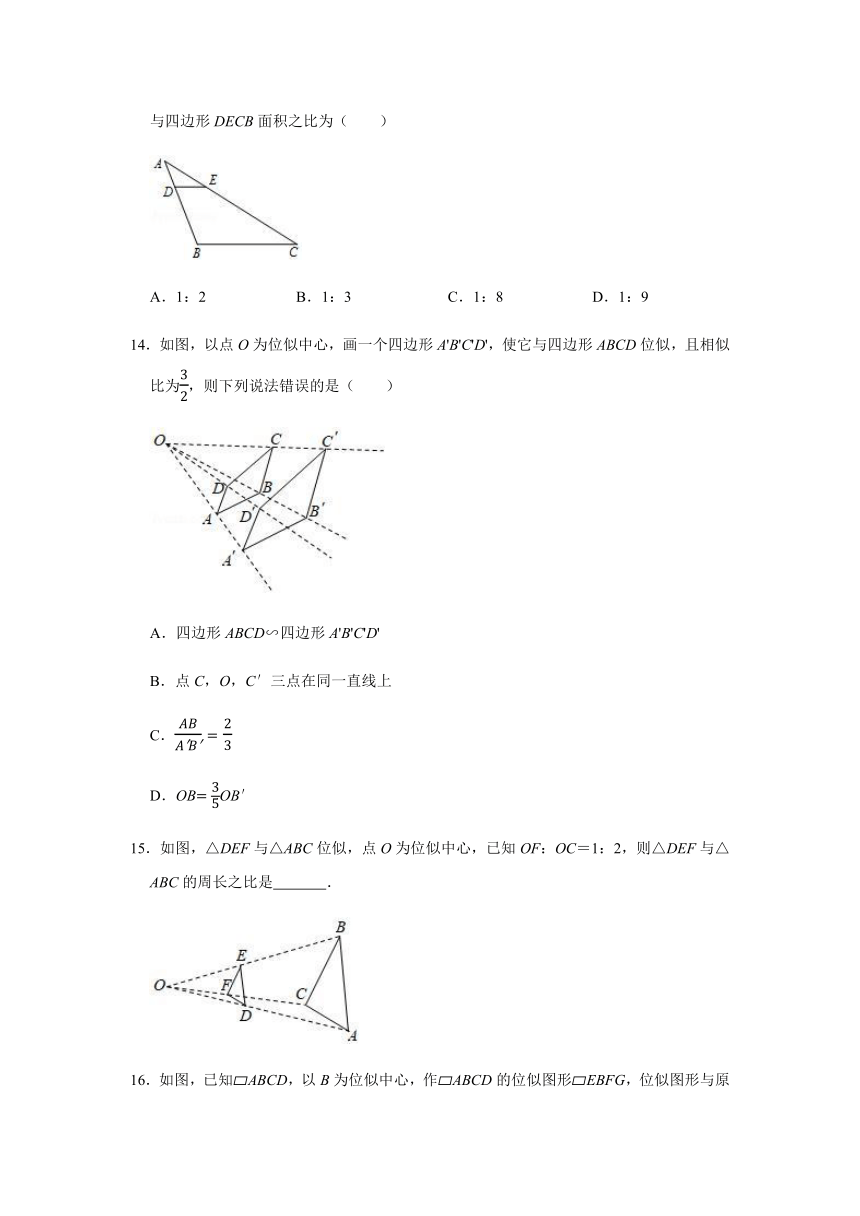
13.如图,△ABC与△ADE成位似图形,位似中心为点A,若AD:AB=1:3,则△ADE与四边形DECB面积之比为( )
A.1:2
B.1:3
C.1:8
D.1:9
14.如图,以点O为位似中心,画一个四边形A'B'C'D',使它与四边形ABCD位似,且相似比为,则下列说法错误的是( )
A.四边形ABCD∽四边形A'B'C'D'
B.点C,O,C′三点在同一直线上
C.
D.OBOB′
15.如图,△DEF与△ABC位似,点O为位似中心,已知OF:OC=1:2,则△DEF与△ABC的周长之比是
.
16.如图,已知?ABCD,以B为位似中心,作?ABCD的位似图形?EBFG,位似图形与原图形的位似比为,连结AG,DG.若?ABCD的面积为24,则△ADG的面积为
.
17.作四边形,使它和已知的四边形位似比等于1:2,位似中心为O使两个图形在点O同侧.(不写作法)
18.图①、图②、图③都是6×6的网格,每个小正方形的顶点称为格点,△ABC的顶点A、B、C均在格点上,在图①、图②、图③中,只用无刻度的直尺,在给定的网格中按要求作图.不要求写出画法.
(1)在图①中画出△ABC边BC上的中线AD,则S△ABD=
;
(2)在图②中画出△BEF,点E、F分别在边AB、BC上,满足△BEF∽△BAC,且S△BEF:S△BAC=1:4;
(3)在图③中画出△BMN,点M、N分别在边AB、BC上,使得△BMN与△BAC是位似图形,且点B为位似中心,位似比为.(保留作图痕迹)
19.如图,△ABC中,P′是边AB上一点,四边形P'Q'M'N'是正方形,点Q',M在边BC上,点N′在△ABC内.连接BN′,并延长交AC于点N,过点N作NM⊥BC于点M,NP⊥MN交AB于点P,PQ⊥BC于点Q.
(1)求证:四边形PQMN为正方形;
(2)若∠A=90°,AC=1.5m,△ABC的面积=1.5m2.求PN的长.
参考答案与试题解析
1.解:如图,点O为两个三角形的位似中心,
∵点M的坐标为(3,2),
∴位似中心O的坐标为(0,2),
故选:A.
2.解:A、全等的图形不一定是位似图形,故此选项错误;
B、相似的图形不一定是位似图形,故此选项错误;
C、位似图形不一定是全等图形,故此选项错误;
D、位似图形一定是相似图形,正确.
故选:D.
3.解:根据位似图形的定义,可得A,C,D是位似图形,A与C的位似中心是交点,D的为中心是圆心;B不是位似图形.
故选:B.
4.解:∵以点O为位似中心,把△ABC放大为原来的2倍,得到△A′B′C′,
∴OB′=2OB,
∴BB′:BO=3:1,所以A选项的说法错误;
∵△A′B′C′和△ABC位似图形,位似中心为O点,
∴△A′B′C′≌△ABC,AB∥A′B′,点C,点O,点C'三点共线,所以B、C、D选项的说法正确.
故选:A.
5.解:∵OD=2AD,
∴,
∵△ABC与△DEF位似,
∴DE∥AB,EF∥BC,
∴,,
∴,即,
解得,EF=4,
故选:C.
6.解:∵△ABC与△DEF位似,
∴DF∥AC,△ABC∽△DEF,
∴△ODF∽△OAC,
∴,
∴△DEF与△ABC的面积比=()2,
∴△ABC与△DEF的面积比为4:1,
故选:B.
7.解:∵六边形ABCDEF与六边形A1B1C1D1E1F1是位似图形,
∴六边形ABCDEF∽六边形A1B1C1D1E1F1,DE∥D′E′,
∴△ODE∽△OD1E1,
∴,
∴2:1,
故选:D.
8.解:画出图形,如图所示:
故选:D.
9.解:由位似图形的画法可得:前3个图形都是△ABC的位似图形.
故选:C.
10.解:(1)如图②,△DFE为所作;
(2)如图③,△A1B1C1为所作.
11.解:根据位似图形的定义可知两个图形不仅是相似图形而且每组对应点所在的直线都经过同一个点,对应边互相平行(或共线),所以位似图形的是第一个、第二个和第三个.
故选:D.
12.解:∵四边形ABCD与四边形A'B'C'D'位似,
∴四边形ABCD∽四边形A'B'C'D',AB∥A′B′,
∴△OAB∽△OA′B′,
∴,
∴四边形ABCD与四边形A'B'C′D'的面积比=()2,
故选:C.
13.解:∵△ABC与△ADE成位似图形,位似中心为点A,
∴△ADE∽△ABC,
∵AD:AB=1:3,
∴S△ADE:S△ABC=1:9,
∴S△ADE:S四边形DBCE=1:8.
故选:C.
14.解:∵四边形A'B'C'D'与四边形ABCD位似,
∴四边形A'B'C'D'∽四边形ABCD,A选项说法正确,不符合题意;
∵四边形A'B'C'D'与四边形ABCD位似,
∴点C,O,C′三点在同一直线上,B选项说法正确,不符合题意;
∵四边形A'B'C'D'与四边形ABCD位似,位似比为,
∴,C选项说法正确,不符合题意;
∵四边形A'B'C'D'与四边形ABCD位似,位似比为,
∴AB∥A′B′,
∴,
∴OBOB′,D选项说法错误,符合题意;
故选:D.
15.解:∵△DEF与△ABC位似,点O为位似中心,
∴△DEF与△ABC的周长之比是:1:2.
故答案为:1:2.
16.解:连接BG,
∵?ABCD和?EBFG是以B为位似中心的位似图形,
∴点D、G、B在同一条直线上,EG∥AD,
∵四边形ABCD是平行四边形,面积为24,
∴△ADB的面积为12,
∵EG∥AD,
∴,
∴,
∴△ADG的面积=124,
故答案为:4.
17.解:如图所示,四边形A′B′C′D′即为所求.
18.解:(1)如图①中,线段AD即为所求.S△ABD3×4=6,
故答案为6.
(2)如图②中,线段EF即为所求.
(3)如图③中,线段MN即为所求.
19.(1)证明:∵NM⊥BC,NP⊥MN,PQ⊥BC,
∴四边形PQMN为矩形,
∵四边形P'Q'M'N'是正方形,
∴PN∥P′N′,
∴,
∵MN∥M′N′,
∴,
∴,
而P′N′=M′N′,
∴PN=MN,
∴四边形PQMN为正方形;
(2)解:作AD⊥BC于D,AD交PN于E,如图,
∵△ABC的面积=1.5,
∴AB?AC=1.5,
∴AB=2,
∴BC2.5,
∵BC?AD=1.5,
∴AD,
设PN=x,则PQ=DE=x,AEx,
∵PN∥BC,
∴△APN∽△ABC,
∴,即,解得x,
即PN的长为m.
第1课时 位似图形
1.如图中的两个三角形是位似图形,点M的坐标为(3,2),则它们位似中心的坐标是( )
A.(0,2)
B.(0,3)
C.(2,﹣1)
D.(2,3
)
2.下列命题中,正确的是( )
A.全等的图形一定是位似图形
B.相似的图形一定是位似图形
C.位似图形一定是全等图形
D.位似图形一定是相似图形
3.下列各组图形中,不是位似图形的是( )
A.
B.
C.
D.
4.如图,以点O为位似中心,把△ABC放大为原来的2倍,得到△A′B′C′,以下说法错误的是( )
A.BB′:BO=2:1
B.△ABC∽△A'B'C'
C.AB∥A'B'
D.点C,点O,点C'三点共线
5.如图,△ABC与△DEF位似,点O是位似中心,且OD=2AD,若BC=6,则EF=( )
A.2
B.3
C.4
D.5
6.如图,△ABC与△DEF位似,其位似中心为点O,且D为AO的中点,则△ABC与△DEF的面积比是( )
A.2:1
B.4:1
C.3:1
D.9:1
7.如图,六边形ABCDEF与六边形A1B1C1D1E1F1是位似图形,O为位似中心,ODOD1,则A1B1:AB为( )
A.2:3
B.3:2
C.1:2
D.2:1
8.如图所示,在平面直角坐标系中,有两点A(4,2),B(3,0),以原点为位似中心,A′B′与AB的相似比为,得到线段A′B′.正确的画法是( )
A.
B.
C.
D.
9.如图所示是△ABC位似图形的几种画法,其中正确的是个数是( )
A.1
B.2
C.3
D.4
10.如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点,以格点为顶点,分别按下列要求画三角形.
(1)在图②中,请在网格中画一个与图①△ABC相似的△DEF;
(2)在图③中,以O为位似中心,画一个△A1B1C1,使它与△ABC的位似比为2:1.
11.下列3个图形中是位似图形的有( )
A.0个
B.1个
C.2个
D.3个
12.如图,四边形ABCD与四边形A'B'C'D'位似,点O为位似中心,若OB:OB'=2:3,则四边形ABCD与四边形A'B'C′D'的面积比为( )
A.2:3
B.2:5
C.4:9
D.4:25
13.如图,△ABC与△ADE成位似图形,位似中心为点A,若AD:AB=1:3,则△ADE与四边形DECB面积之比为( )
A.1:2
B.1:3
C.1:8
D.1:9
14.如图,以点O为位似中心,画一个四边形A'B'C'D',使它与四边形ABCD位似,且相似比为,则下列说法错误的是( )
A.四边形ABCD∽四边形A'B'C'D'
B.点C,O,C′三点在同一直线上
C.
D.OBOB′
15.如图,△DEF与△ABC位似,点O为位似中心,已知OF:OC=1:2,则△DEF与△ABC的周长之比是
.
16.如图,已知?ABCD,以B为位似中心,作?ABCD的位似图形?EBFG,位似图形与原图形的位似比为,连结AG,DG.若?ABCD的面积为24,则△ADG的面积为
.
17.作四边形,使它和已知的四边形位似比等于1:2,位似中心为O使两个图形在点O同侧.(不写作法)
18.图①、图②、图③都是6×6的网格,每个小正方形的顶点称为格点,△ABC的顶点A、B、C均在格点上,在图①、图②、图③中,只用无刻度的直尺,在给定的网格中按要求作图.不要求写出画法.
(1)在图①中画出△ABC边BC上的中线AD,则S△ABD=
;
(2)在图②中画出△BEF,点E、F分别在边AB、BC上,满足△BEF∽△BAC,且S△BEF:S△BAC=1:4;
(3)在图③中画出△BMN,点M、N分别在边AB、BC上,使得△BMN与△BAC是位似图形,且点B为位似中心,位似比为.(保留作图痕迹)
19.如图,△ABC中,P′是边AB上一点,四边形P'Q'M'N'是正方形,点Q',M在边BC上,点N′在△ABC内.连接BN′,并延长交AC于点N,过点N作NM⊥BC于点M,NP⊥MN交AB于点P,PQ⊥BC于点Q.
(1)求证:四边形PQMN为正方形;
(2)若∠A=90°,AC=1.5m,△ABC的面积=1.5m2.求PN的长.
参考答案与试题解析
1.解:如图,点O为两个三角形的位似中心,
∵点M的坐标为(3,2),
∴位似中心O的坐标为(0,2),
故选:A.
2.解:A、全等的图形不一定是位似图形,故此选项错误;
B、相似的图形不一定是位似图形,故此选项错误;
C、位似图形不一定是全等图形,故此选项错误;
D、位似图形一定是相似图形,正确.
故选:D.
3.解:根据位似图形的定义,可得A,C,D是位似图形,A与C的位似中心是交点,D的为中心是圆心;B不是位似图形.
故选:B.
4.解:∵以点O为位似中心,把△ABC放大为原来的2倍,得到△A′B′C′,
∴OB′=2OB,
∴BB′:BO=3:1,所以A选项的说法错误;
∵△A′B′C′和△ABC位似图形,位似中心为O点,
∴△A′B′C′≌△ABC,AB∥A′B′,点C,点O,点C'三点共线,所以B、C、D选项的说法正确.
故选:A.
5.解:∵OD=2AD,
∴,
∵△ABC与△DEF位似,
∴DE∥AB,EF∥BC,
∴,,
∴,即,
解得,EF=4,
故选:C.
6.解:∵△ABC与△DEF位似,
∴DF∥AC,△ABC∽△DEF,
∴△ODF∽△OAC,
∴,
∴△DEF与△ABC的面积比=()2,
∴△ABC与△DEF的面积比为4:1,
故选:B.
7.解:∵六边形ABCDEF与六边形A1B1C1D1E1F1是位似图形,
∴六边形ABCDEF∽六边形A1B1C1D1E1F1,DE∥D′E′,
∴△ODE∽△OD1E1,
∴,
∴2:1,
故选:D.
8.解:画出图形,如图所示:
故选:D.
9.解:由位似图形的画法可得:前3个图形都是△ABC的位似图形.
故选:C.
10.解:(1)如图②,△DFE为所作;
(2)如图③,△A1B1C1为所作.
11.解:根据位似图形的定义可知两个图形不仅是相似图形而且每组对应点所在的直线都经过同一个点,对应边互相平行(或共线),所以位似图形的是第一个、第二个和第三个.
故选:D.
12.解:∵四边形ABCD与四边形A'B'C'D'位似,
∴四边形ABCD∽四边形A'B'C'D',AB∥A′B′,
∴△OAB∽△OA′B′,
∴,
∴四边形ABCD与四边形A'B'C′D'的面积比=()2,
故选:C.
13.解:∵△ABC与△ADE成位似图形,位似中心为点A,
∴△ADE∽△ABC,
∵AD:AB=1:3,
∴S△ADE:S△ABC=1:9,
∴S△ADE:S四边形DBCE=1:8.
故选:C.
14.解:∵四边形A'B'C'D'与四边形ABCD位似,
∴四边形A'B'C'D'∽四边形ABCD,A选项说法正确,不符合题意;
∵四边形A'B'C'D'与四边形ABCD位似,
∴点C,O,C′三点在同一直线上,B选项说法正确,不符合题意;
∵四边形A'B'C'D'与四边形ABCD位似,位似比为,
∴,C选项说法正确,不符合题意;
∵四边形A'B'C'D'与四边形ABCD位似,位似比为,
∴AB∥A′B′,
∴,
∴OBOB′,D选项说法错误,符合题意;
故选:D.
15.解:∵△DEF与△ABC位似,点O为位似中心,
∴△DEF与△ABC的周长之比是:1:2.
故答案为:1:2.
16.解:连接BG,
∵?ABCD和?EBFG是以B为位似中心的位似图形,
∴点D、G、B在同一条直线上,EG∥AD,
∵四边形ABCD是平行四边形,面积为24,
∴△ADB的面积为12,
∵EG∥AD,
∴,
∴,
∴△ADG的面积=124,
故答案为:4.
17.解:如图所示,四边形A′B′C′D′即为所求.
18.解:(1)如图①中,线段AD即为所求.S△ABD3×4=6,
故答案为6.
(2)如图②中,线段EF即为所求.
(3)如图③中,线段MN即为所求.
19.(1)证明:∵NM⊥BC,NP⊥MN,PQ⊥BC,
∴四边形PQMN为矩形,
∵四边形P'Q'M'N'是正方形,
∴PN∥P′N′,
∴,
∵MN∥M′N′,
∴,
∴,
而P′N′=M′N′,
∴PN=MN,
∴四边形PQMN为正方形;
(2)解:作AD⊥BC于D,AD交PN于E,如图,
∵△ABC的面积=1.5,
∴AB?AC=1.5,
∴AB=2,
∴BC2.5,
∵BC?AD=1.5,
∴AD,
设PN=x,则PQ=DE=x,AEx,
∵PN∥BC,
∴△APN∽△ABC,
∴,即,解得x,
即PN的长为m.
