27.3 第2课时 用坐标描述位似变换-2020-2021学年人教版九年级数学下册同步练习 (1)(word版含答案)
文档属性
| 名称 | 27.3 第2课时 用坐标描述位似变换-2020-2021学年人教版九年级数学下册同步练习 (1)(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 484.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-22 10:41:51 | ||
图片预览



文档简介
27.3 位 似
第2课时 用坐标描述位似变换
1.如图,在平面直角坐标系xOy中,已知△ABO的两个顶点分别为A(﹣8,4),B(﹣2,﹣2),以原点O为位似中心画△A′B′O,使它与△ABO位似,且相似比为,则点A的对应点A'的坐标为( )
A.(4,2)
B.(1,1)
C.(﹣4,2)
D.(4,﹣2)
2.如图,在平面直角坐标系中,已知△ABC中点B的坐标为(4,2),以坐标原点O为位似中心,在第三象限内,将△ABC边长放大2倍得到了△A′B′C′,则点B对应点B′的坐标为( )
A.(﹣4,﹣8)
B.(﹣8,﹣4)
C.(﹣6,﹣4)
D.(8,4)
3.如图,在平面直角坐标系中有两点C(2,1)、D(2,0),以原点O为位似中心,相似比为3:1,在第一象限内把线段CD放大后得到线段AB,则点A的坐标为( )
A.(6,0)
B.(3,6)
C.(6,3)
D.(4,2)
4.在平面直角坐标系中,矩形OABC的顶点坐标分别是O(0,0),A(8,0),B(8,6),C(0,6).已知矩形OA1B1C1O与矩形OABC位似,位似中心是原点O,且矩形OA1B1C1的面积等于矩形OABC面积的,则点B1的坐标为( )
A.(4,3)
B.(4,3)或(﹣4,﹣3)
C.(4,3)
D.(4,3)或(﹣4,﹣3)
5.在平面直角坐标系中,已知A(﹣3,3),B(﹣6,0),以原点O为位似中心,将线段AB放大为原来的2倍,得到线段A′B′,则A′B′的中点坐标是
.
6.平面直角坐标系中,有一条鱼,它有六个顶点,则( )
A.将各点横坐标乘2,纵坐标不变,得到的鱼与原来的鱼位似
B.将各点纵坐标乘2,横坐标不变,得到的鱼与原来的鱼位似
C.将各点横,纵坐标都乘2,得到的鱼与原来的鱼位似
D.将各点横坐标乘2,纵坐标乘,得到的鱼与原来的鱼位似
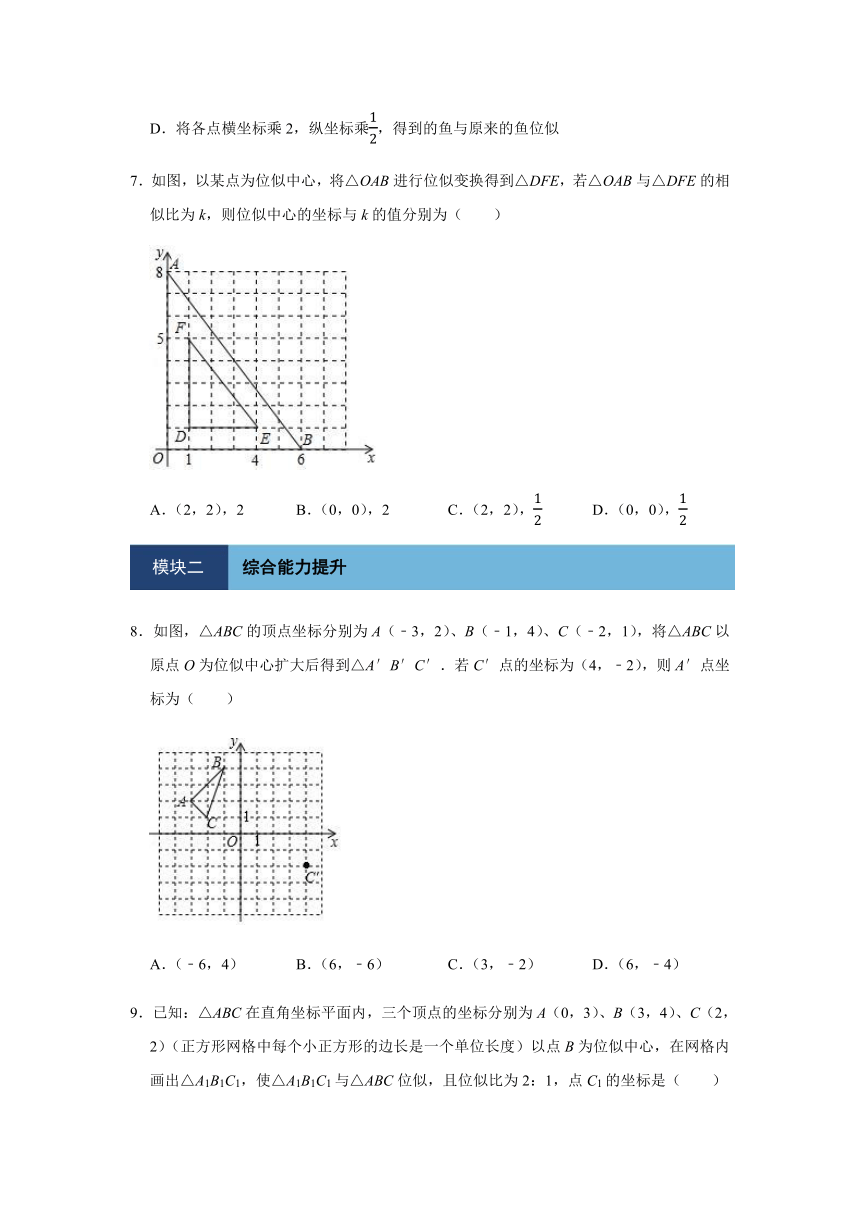
7.如图,以某点为位似中心,将△OAB进行位似变换得到△DFE,若△OAB与△DFE的相似比为k,则位似中心的坐标与k的值分别为( )
A.(2,2),2
B.(0,0),2
C.(2,2),
D.(0,0),
8.如图,△ABC的顶点坐标分别为A(﹣3,2)、B(﹣1,4)、C(﹣2,1),将△ABC以原点O为位似中心扩大后得到△A′B′C′.若C′点的坐标为(4,﹣2),则A′点坐标为( )
A.(﹣6,4)
B.(6,﹣6)
C.(3,﹣2)
D.(6,﹣4)
9.已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度)以点B为位似中心,在网格内画出△A1B1C1,使△A1B1C1与△ABC位似,且位似比为2:1,点C1的坐标是( )
A.(1,0)
B.(1,1)
C.(﹣3,2)
D.(0,0)
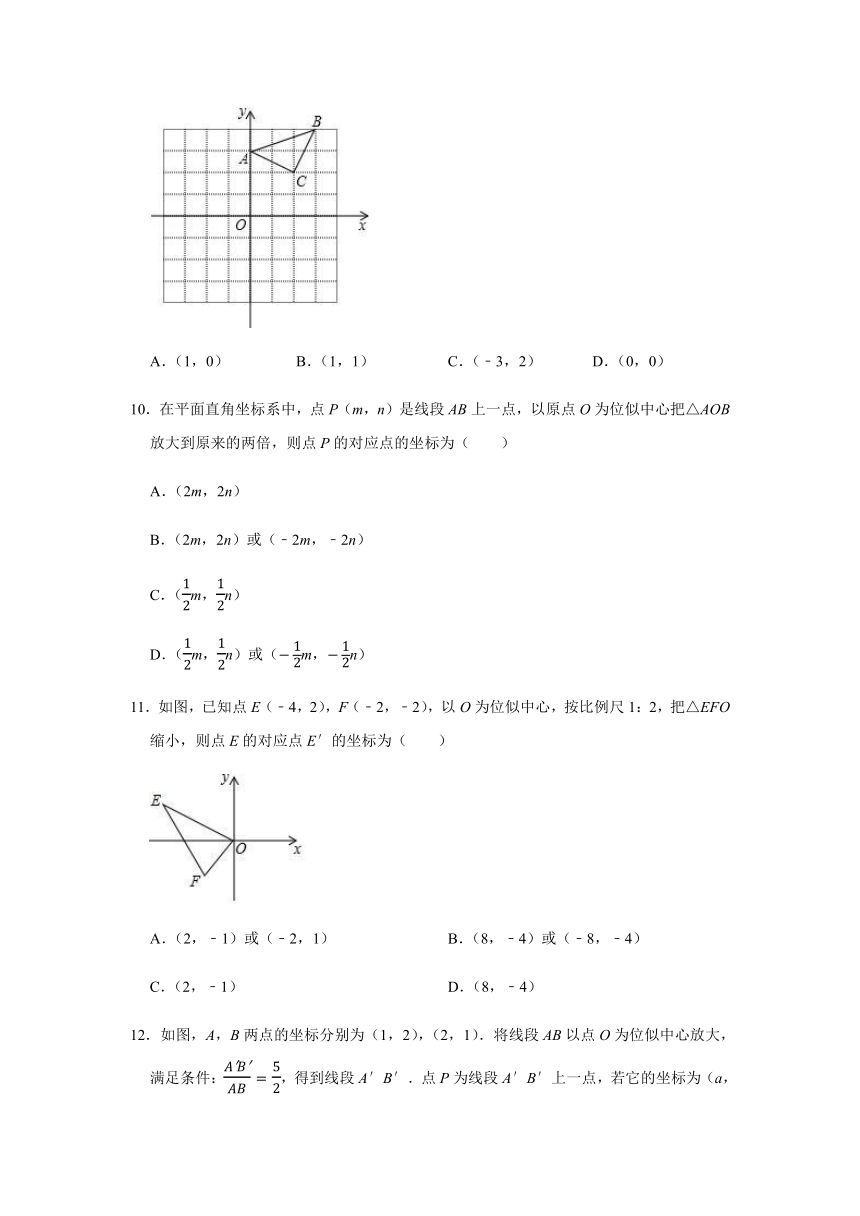
10.在平面直角坐标系中,点P(m,n)是线段AB上一点,以原点O为位似中心把△AOB放大到原来的两倍,则点P的对应点的坐标为( )
A.(2m,2n)
B.(2m,2n)或(﹣2m,﹣2n)
C.(m,n)
D.(m,n)或(m,n)
11.如图,已知点E(﹣4,2),F(﹣2,﹣2),以O为位似中心,按比例尺1:2,把△EFO缩小,则点E的对应点E′的坐标为( )
A.(2,﹣1)或(﹣2,1)
B.(8,﹣4)或(﹣8,﹣4)
C.(2,﹣1)
D.(8,﹣4)
12.如图,A,B两点的坐标分别为(1,2),(2,1).将线段AB以点O为位似中心放大,满足条件:,得到线段A′B′.点P为线段A′B′上一点,若它的坐标为(a,b),则它在线段AB上的对应点的坐标为( )
A.(a,b)
B.(a,b)
C.(a,b)
D.(a,b)
13.已知,在平面直角坐标系中,正方形A1B1C1A2与正方形A2B2C2A3是以原点O为位似中心的位似图形,且相似比为,点A1,A2,A3在x轴上,延长A3C2交射线OB1于点B3,以A3B3为边长作正方形A3B3C3A4;延长A4C3交射线OB1于点B4,以A4B4为边长作正方形A4B4C4A5…,若OA1=2,则正方形AnBn?nAn+1的面积为( )
A.2n
B.2n
C.2n+1
D.4n
14.如图,在平面直角坐标系中,△ABC与△DOE是位似图形.若A(0,3)、B(﹣2,
0)、C(1,0)、E(6,0),△ABC与△DOE的位似中心是点M,则M点的坐标为
.
15.如图,在直角坐标系中,△ABC的各顶点坐标为A(﹣1,1),B(2,3),C(0,3).现以坐标原点为位似中心,作△A′B′C′,使△A′B′C′与△ABC的位似比为.则点A的对应点A′的坐标为
.
16.如图,△ABC中,A、B两点在x轴的上方,点C的坐标是(﹣1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点B的对应点B′的横坐标是2,求点B的横坐标.
17.如图△ABC的顶点坐标分别为A(1,1),B(2,3),C(3,0).
(1)以点O为位似中心画△DEF,使它与△ABC位似,且相似比为2.
(2)在(1)的条件下,若M(a,b)为△ABC边上的任意一点,则△DEF的边上与点M对应的点M′的坐标为
.
18.如图,?ABCD的对角线AC、BD相交于点O,点E、F、G、H分别是线段OA、OB、OC、OD的中点,那么?ABCD与四边形EFGH是否是位似图形?为什么?
19.如图1,△ABC为等边三角形,△ADE是△ABC的位似图形,位似比为k:1,点D在AB上,点E在AC上,点E在AC上.
(1)证明:DE∥BC.
(2)将△ADE绕点A旋转α至△AMN的位置,如图2,当AM⊥BC时,请你判断AC与MN的位置关系,并说明理由.
参考答案与试题解析
1.解:∵△ABO的两个顶点分别为A(﹣8,4),B(﹣2,﹣2),以原点O为位似中心画△A′B′O,使它与△ABO位似,且相似比为,
∴点A的对应点A'的坐标为:[﹣8×(),4×()]即(4,﹣2).
故选:D.
2.解:∵△ABC中点B的坐标为(4,2),以坐标原点O为位似中心,在第三象限内,将△ABC边长放大2倍得到了△A′B′C′,
∴点B对应点B′的坐标为:[4×(﹣2),2×(﹣2)]即(﹣8,﹣4).
故选:B.
3.解:∵以原点O为位似中心,相似比为3:1,在第一象限内把线段CD放大后得到线段AB,点C的坐标为(2,1),
∴点A的坐标为(2×3,1×3),即(6,3),
故选:C.
4.解:∵矩形OA1B1C1O与矩形OABC位似,矩形OA1B1C1的面积等于矩形OABC面积的,
∴矩形OA1B1C1O与矩形OABC的位似比为1:,
∵矩形OA1B1C1O与矩形OABC位似,位似中心是原点O,点B的坐标为(8,6),
∴点B1的坐标为为(8,6)或(﹣8,﹣6),即(4,3)或(4,3),
故选:D.
5.解:∵点A的坐标为(﹣3,3),点B的坐标为(﹣6,0),
∴AB的中点坐标为(,),
∵以原点O为位似中心,将线段AB放大为原来的2倍,得到线段A′B′,
∴A′B′的中点坐标是(2,2)或(2,2),即(﹣9,3)或(9,﹣3),
故答案为:(﹣9,3)或(9,﹣3).
6.解:平面直角坐标系中图形的各个顶点,如果横纵坐标同时乘以同一个非0的实数k,得到的图形与原图形关于原点成位似图形,位似比是|k|.若乘的不是同一个数,得到的图形一定不会与原图形关于原点对称.故选C.
7.解:连接OD、BE,延长OD交BE的延长线于点O′,点O′也就是位似中心为(2,2);
k=OA:FD=8:4=2,
故选:A.
8.解:∵△ABC的顶点坐标分别为A(﹣3,2)、B(﹣1,4)、C(﹣2,1),将△ABC以原点O为位似中心扩大后得到△A′B′C′.C′点的坐标为(4,﹣2),
∴对应点的坐标乘以﹣2,故A′点坐标为:(6,﹣4).
故选:D.
9.解:如图所示:点C1的坐标是:(1,0).
故选:A.
10.解:点P(m,n)是线段AB上一点,以原点O为位似中心把△AOB放大到原来的两倍,
则点P的对应点的坐标为(m×2,n×2)或(m×(﹣2),n×(﹣2)),即(2m,2n)或(﹣2m,﹣2n),
故选:B.
11.解:以O为位似中心,按比例尺1:2,把△EFO缩小,
则点E的对应点E′的坐标为(﹣4,2)或[﹣4×(),2×()],
即(2,﹣1)或(﹣2,1),
故选:A.
12.解:∵,
∴,
即,
∵P(a,b),
∴点P在线段AB上的对应点的坐标为(a,b).
故选:A.
13.解:∵正方形A1B1C1A2与正方形A2B2C2A3是以原点O为位似中心的位似图形,且相似比为,
∴,
∵A1B1⊥x轴,A2B2⊥x轴,
∴A1B1∥A2B2,
∴OA1B1∽△OA2B2,
∴,
∵OA1=2,
∴OA2=4,
∴A1A2=2,
∴正方形A1B1C1A2的面积=2×2=4,
∵OA1=A1A2=A1B1=2,
∴∠B1OA1=45°,
∴OA2=A2B2=4,
∴正方形A2B2C2A3的面积=4×4=42,
∵A3B3⊥x轴,
∴OA3=A3B3=8,
∴正方形A3B3C3A4的面积=8×8=64=43,
…
∴正方形AnBn?nAn+1的面积=4n,
故选:D.
14.解:过点D作DH⊥OE于点H,
由题意可得:BC=3,OE=6,△ABC∽△DOE,
则位似比为:3:6=1:2,
故OH=2OB=4,DH=2OA=6,
则D点的坐标为:(4,6),
由MO:MH=1:2,
MH=MO+4,
故MO:(MO+4)=1:2,
解得:MO=4,
则M点坐标为:(﹣4,0).
故答案为:(﹣4,0).
15.解:∵在△A′B′C′中,它的对应点的坐标是(kx,ky)或(﹣kx,﹣ky)
∴A'的坐标为:(,)或(,).
故答案为:(,)或(,).
16.解:过点B、B'分别作BD⊥x轴于D,B'E⊥x轴于E,
∴∠BDC=∠B'EC=90°.
∵△ABC的位似图形是△A'B'C,
∴点B、C、B'在一条直线上,
∴∠BCD=∠B'CE,
∴△BCD∽△B'CE.
∴,
又∵,
∴,
又∵点B'的横坐标是2,点C的坐标是(﹣1,0),
∴CE=3,
∴.
∴,
∴点B的横坐标为.
17.解:(1)如图,△DEF和△D′E′F′为所作;
(2)点M对应的点M′的坐标为(2a,2b)或(﹣2a,﹣2b).
故答案为(2a,2b)或(﹣2a,﹣2b).
18.解:是,
理由:∵E、F分别是OA、OB的中点,
∴FEAB,FE∥AB,
G、H分别是OC、OD的中点,
∴HGCD,HG∥CD,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴EF=HG,FE∥HG,
∴四边形EFGH是平行四边形;
∵FE∥AB,
∴∠OEF=∠OAB,
同理∠OEH=∠OAD,
∴∠HEF=∠DAB,
同理,∠EFG=∠ABC,∠FGH=∠BCD,∠GHE=∠CDA,,
∴平行四边形EFGH∽平行四边形ABCD,
又∵各组对边对应点得连线相交于点O,
∴平行四边形ABCD与四边形EFGH是位似图形,O为位似中心.
19.(1)证明:∵△ADE是△ABC的位似图形,
∴△ADE∽△ABC,
∴∠ADE=∠B,
∴DE∥BC;
(2)AC⊥MN.
证明:如图2,延长AM交BC于D,
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∴∠DAC=30°,又∠AMN=60°,
∴∠AFM=90°,即AC⊥MN.
第2课时 用坐标描述位似变换
1.如图,在平面直角坐标系xOy中,已知△ABO的两个顶点分别为A(﹣8,4),B(﹣2,﹣2),以原点O为位似中心画△A′B′O,使它与△ABO位似,且相似比为,则点A的对应点A'的坐标为( )
A.(4,2)
B.(1,1)
C.(﹣4,2)
D.(4,﹣2)
2.如图,在平面直角坐标系中,已知△ABC中点B的坐标为(4,2),以坐标原点O为位似中心,在第三象限内,将△ABC边长放大2倍得到了△A′B′C′,则点B对应点B′的坐标为( )
A.(﹣4,﹣8)
B.(﹣8,﹣4)
C.(﹣6,﹣4)
D.(8,4)
3.如图,在平面直角坐标系中有两点C(2,1)、D(2,0),以原点O为位似中心,相似比为3:1,在第一象限内把线段CD放大后得到线段AB,则点A的坐标为( )
A.(6,0)
B.(3,6)
C.(6,3)
D.(4,2)
4.在平面直角坐标系中,矩形OABC的顶点坐标分别是O(0,0),A(8,0),B(8,6),C(0,6).已知矩形OA1B1C1O与矩形OABC位似,位似中心是原点O,且矩形OA1B1C1的面积等于矩形OABC面积的,则点B1的坐标为( )
A.(4,3)
B.(4,3)或(﹣4,﹣3)
C.(4,3)
D.(4,3)或(﹣4,﹣3)
5.在平面直角坐标系中,已知A(﹣3,3),B(﹣6,0),以原点O为位似中心,将线段AB放大为原来的2倍,得到线段A′B′,则A′B′的中点坐标是
.
6.平面直角坐标系中,有一条鱼,它有六个顶点,则( )
A.将各点横坐标乘2,纵坐标不变,得到的鱼与原来的鱼位似
B.将各点纵坐标乘2,横坐标不变,得到的鱼与原来的鱼位似
C.将各点横,纵坐标都乘2,得到的鱼与原来的鱼位似
D.将各点横坐标乘2,纵坐标乘,得到的鱼与原来的鱼位似
7.如图,以某点为位似中心,将△OAB进行位似变换得到△DFE,若△OAB与△DFE的相似比为k,则位似中心的坐标与k的值分别为( )
A.(2,2),2
B.(0,0),2
C.(2,2),
D.(0,0),
8.如图,△ABC的顶点坐标分别为A(﹣3,2)、B(﹣1,4)、C(﹣2,1),将△ABC以原点O为位似中心扩大后得到△A′B′C′.若C′点的坐标为(4,﹣2),则A′点坐标为( )
A.(﹣6,4)
B.(6,﹣6)
C.(3,﹣2)
D.(6,﹣4)
9.已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度)以点B为位似中心,在网格内画出△A1B1C1,使△A1B1C1与△ABC位似,且位似比为2:1,点C1的坐标是( )
A.(1,0)
B.(1,1)
C.(﹣3,2)
D.(0,0)
10.在平面直角坐标系中,点P(m,n)是线段AB上一点,以原点O为位似中心把△AOB放大到原来的两倍,则点P的对应点的坐标为( )
A.(2m,2n)
B.(2m,2n)或(﹣2m,﹣2n)
C.(m,n)
D.(m,n)或(m,n)
11.如图,已知点E(﹣4,2),F(﹣2,﹣2),以O为位似中心,按比例尺1:2,把△EFO缩小,则点E的对应点E′的坐标为( )
A.(2,﹣1)或(﹣2,1)
B.(8,﹣4)或(﹣8,﹣4)
C.(2,﹣1)
D.(8,﹣4)
12.如图,A,B两点的坐标分别为(1,2),(2,1).将线段AB以点O为位似中心放大,满足条件:,得到线段A′B′.点P为线段A′B′上一点,若它的坐标为(a,b),则它在线段AB上的对应点的坐标为( )
A.(a,b)
B.(a,b)
C.(a,b)
D.(a,b)
13.已知,在平面直角坐标系中,正方形A1B1C1A2与正方形A2B2C2A3是以原点O为位似中心的位似图形,且相似比为,点A1,A2,A3在x轴上,延长A3C2交射线OB1于点B3,以A3B3为边长作正方形A3B3C3A4;延长A4C3交射线OB1于点B4,以A4B4为边长作正方形A4B4C4A5…,若OA1=2,则正方形AnBn?nAn+1的面积为( )
A.2n
B.2n
C.2n+1
D.4n
14.如图,在平面直角坐标系中,△ABC与△DOE是位似图形.若A(0,3)、B(﹣2,
0)、C(1,0)、E(6,0),△ABC与△DOE的位似中心是点M,则M点的坐标为
.
15.如图,在直角坐标系中,△ABC的各顶点坐标为A(﹣1,1),B(2,3),C(0,3).现以坐标原点为位似中心,作△A′B′C′,使△A′B′C′与△ABC的位似比为.则点A的对应点A′的坐标为
.
16.如图,△ABC中,A、B两点在x轴的上方,点C的坐标是(﹣1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点B的对应点B′的横坐标是2,求点B的横坐标.
17.如图△ABC的顶点坐标分别为A(1,1),B(2,3),C(3,0).
(1)以点O为位似中心画△DEF,使它与△ABC位似,且相似比为2.
(2)在(1)的条件下,若M(a,b)为△ABC边上的任意一点,则△DEF的边上与点M对应的点M′的坐标为
.
18.如图,?ABCD的对角线AC、BD相交于点O,点E、F、G、H分别是线段OA、OB、OC、OD的中点,那么?ABCD与四边形EFGH是否是位似图形?为什么?
19.如图1,△ABC为等边三角形,△ADE是△ABC的位似图形,位似比为k:1,点D在AB上,点E在AC上,点E在AC上.
(1)证明:DE∥BC.
(2)将△ADE绕点A旋转α至△AMN的位置,如图2,当AM⊥BC时,请你判断AC与MN的位置关系,并说明理由.
参考答案与试题解析
1.解:∵△ABO的两个顶点分别为A(﹣8,4),B(﹣2,﹣2),以原点O为位似中心画△A′B′O,使它与△ABO位似,且相似比为,
∴点A的对应点A'的坐标为:[﹣8×(),4×()]即(4,﹣2).
故选:D.
2.解:∵△ABC中点B的坐标为(4,2),以坐标原点O为位似中心,在第三象限内,将△ABC边长放大2倍得到了△A′B′C′,
∴点B对应点B′的坐标为:[4×(﹣2),2×(﹣2)]即(﹣8,﹣4).
故选:B.
3.解:∵以原点O为位似中心,相似比为3:1,在第一象限内把线段CD放大后得到线段AB,点C的坐标为(2,1),
∴点A的坐标为(2×3,1×3),即(6,3),
故选:C.
4.解:∵矩形OA1B1C1O与矩形OABC位似,矩形OA1B1C1的面积等于矩形OABC面积的,
∴矩形OA1B1C1O与矩形OABC的位似比为1:,
∵矩形OA1B1C1O与矩形OABC位似,位似中心是原点O,点B的坐标为(8,6),
∴点B1的坐标为为(8,6)或(﹣8,﹣6),即(4,3)或(4,3),
故选:D.
5.解:∵点A的坐标为(﹣3,3),点B的坐标为(﹣6,0),
∴AB的中点坐标为(,),
∵以原点O为位似中心,将线段AB放大为原来的2倍,得到线段A′B′,
∴A′B′的中点坐标是(2,2)或(2,2),即(﹣9,3)或(9,﹣3),
故答案为:(﹣9,3)或(9,﹣3).
6.解:平面直角坐标系中图形的各个顶点,如果横纵坐标同时乘以同一个非0的实数k,得到的图形与原图形关于原点成位似图形,位似比是|k|.若乘的不是同一个数,得到的图形一定不会与原图形关于原点对称.故选C.
7.解:连接OD、BE,延长OD交BE的延长线于点O′,点O′也就是位似中心为(2,2);
k=OA:FD=8:4=2,
故选:A.
8.解:∵△ABC的顶点坐标分别为A(﹣3,2)、B(﹣1,4)、C(﹣2,1),将△ABC以原点O为位似中心扩大后得到△A′B′C′.C′点的坐标为(4,﹣2),
∴对应点的坐标乘以﹣2,故A′点坐标为:(6,﹣4).
故选:D.
9.解:如图所示:点C1的坐标是:(1,0).
故选:A.
10.解:点P(m,n)是线段AB上一点,以原点O为位似中心把△AOB放大到原来的两倍,
则点P的对应点的坐标为(m×2,n×2)或(m×(﹣2),n×(﹣2)),即(2m,2n)或(﹣2m,﹣2n),
故选:B.
11.解:以O为位似中心,按比例尺1:2,把△EFO缩小,
则点E的对应点E′的坐标为(﹣4,2)或[﹣4×(),2×()],
即(2,﹣1)或(﹣2,1),
故选:A.
12.解:∵,
∴,
即,
∵P(a,b),
∴点P在线段AB上的对应点的坐标为(a,b).
故选:A.
13.解:∵正方形A1B1C1A2与正方形A2B2C2A3是以原点O为位似中心的位似图形,且相似比为,
∴,
∵A1B1⊥x轴,A2B2⊥x轴,
∴A1B1∥A2B2,
∴OA1B1∽△OA2B2,
∴,
∵OA1=2,
∴OA2=4,
∴A1A2=2,
∴正方形A1B1C1A2的面积=2×2=4,
∵OA1=A1A2=A1B1=2,
∴∠B1OA1=45°,
∴OA2=A2B2=4,
∴正方形A2B2C2A3的面积=4×4=42,
∵A3B3⊥x轴,
∴OA3=A3B3=8,
∴正方形A3B3C3A4的面积=8×8=64=43,
…
∴正方形AnBn?nAn+1的面积=4n,
故选:D.
14.解:过点D作DH⊥OE于点H,
由题意可得:BC=3,OE=6,△ABC∽△DOE,
则位似比为:3:6=1:2,
故OH=2OB=4,DH=2OA=6,
则D点的坐标为:(4,6),
由MO:MH=1:2,
MH=MO+4,
故MO:(MO+4)=1:2,
解得:MO=4,
则M点坐标为:(﹣4,0).
故答案为:(﹣4,0).
15.解:∵在△A′B′C′中,它的对应点的坐标是(kx,ky)或(﹣kx,﹣ky)
∴A'的坐标为:(,)或(,).
故答案为:(,)或(,).
16.解:过点B、B'分别作BD⊥x轴于D,B'E⊥x轴于E,
∴∠BDC=∠B'EC=90°.
∵△ABC的位似图形是△A'B'C,
∴点B、C、B'在一条直线上,
∴∠BCD=∠B'CE,
∴△BCD∽△B'CE.
∴,
又∵,
∴,
又∵点B'的横坐标是2,点C的坐标是(﹣1,0),
∴CE=3,
∴.
∴,
∴点B的横坐标为.
17.解:(1)如图,△DEF和△D′E′F′为所作;
(2)点M对应的点M′的坐标为(2a,2b)或(﹣2a,﹣2b).
故答案为(2a,2b)或(﹣2a,﹣2b).
18.解:是,
理由:∵E、F分别是OA、OB的中点,
∴FEAB,FE∥AB,
G、H分别是OC、OD的中点,
∴HGCD,HG∥CD,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴EF=HG,FE∥HG,
∴四边形EFGH是平行四边形;
∵FE∥AB,
∴∠OEF=∠OAB,
同理∠OEH=∠OAD,
∴∠HEF=∠DAB,
同理,∠EFG=∠ABC,∠FGH=∠BCD,∠GHE=∠CDA,,
∴平行四边形EFGH∽平行四边形ABCD,
又∵各组对边对应点得连线相交于点O,
∴平行四边形ABCD与四边形EFGH是位似图形,O为位似中心.
19.(1)证明:∵△ADE是△ABC的位似图形,
∴△ADE∽△ABC,
∴∠ADE=∠B,
∴DE∥BC;
(2)AC⊥MN.
证明:如图2,延长AM交BC于D,
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∴∠DAC=30°,又∠AMN=60°,
∴∠AFM=90°,即AC⊥MN.
