2020-2021学年八年级数学人教版下册 17.2 勾股定理的逆定理 课后练习2(Word版 含答案)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册 17.2 勾股定理的逆定理 课后练习2(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 304.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-22 00:00:00 | ||
图片预览

文档简介
人教版八年级数学下册
第十七章
勾股定理
17.2
勾股定理的逆定理
课后练习2
一、选择题
1.在中,、、的对应边分别是a、b、c,下列条件中不能说明是直角三角形的是(
)
A.
B.
C.
D.
2.下列条件能使(a,b,c为的三边长)为直角三角形的是(
)
A.
B.
C.
D.
3.如图,在的正方形网格中,的度数是(
)
A.22.5°
B.30°
C.45°
D.60°
4.在中,是直线上一点,已知,,,,则的长为(
)
A.4或14
B.10或14
C.14
D.10
5.△ABC的三边的长a、b、c满足:,则△ABC的形状为(
).
A.等腰三角形
B.等边三角形
C.钝角三角形
D.直角三角形
6.如图,已知中,的垂直平分线分别交于连接,则的长为(
)
A.
B.
C.
D.
7.中,,,BC边上中线,则AB,AC关系为
A.
B.
C.
D.无法确定
8.已知的三边长分别为a,b,c,且这三边长满足,则最长边上的高h=()
A.3
B.4
C.5
D.
9.下列三角形中,是直角三角形的是(
).
A.三角形的三边满足关系a+b=c
B.三角形的三边为9,40,41
C.三角形的一边等于另一边的一半
D.三角形的三边比为1∶2∶3
10.已知三角形的三边长分别为a,b,c,且a+b=10,ab=18,c=8,则该三角形的形状是(
)
A.等腰三角形
B.直角三角形
C.钝角三角形
D.等腰直角三角形
二、填空题
11.在△ABC中,AC=BC=,AB=2,则△ABC中的最小角是_____.
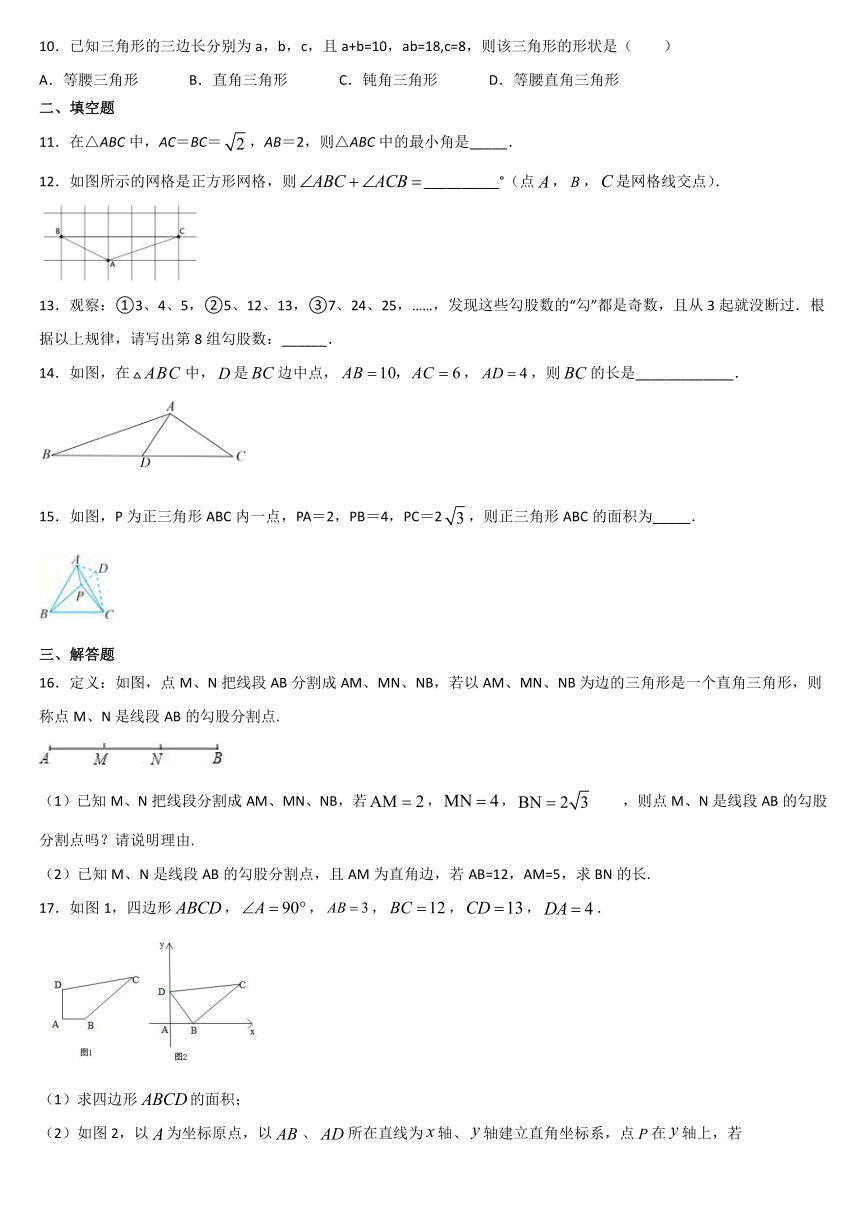
12.如图所示的网格是正方形网格,则__________°(点,,是网格线交点).
13.观察:①3、4、5,②5、12、13,③7、24、25,……,发现这些勾股数的“勾”都是奇数,且从3起就没断过.根据以上规律,请写出第8组勾股数:______.
14.如图,在中,是边中点,,,则的长是_____________.
15.如图,P为正三角形ABC内一点,PA=2,PB=4,PC=2,则正三角形ABC的面积为_____.
三、解答题
16.定义:如图,点M、N把线段AB分割成AM、MN、NB,若以AM、MN、NB为边的三角形是一个直角三角形,则称点M、N是线段AB的勾股分割点.
(1)已知M、N把线段分割成AM、MN、NB,若,,,则点M、N是线段AB的勾股分割点吗?请说明理由.
(2)已知M、N是线段AB的勾股分割点,且AM为直角边,若AB=12,AM=5,求BN的长.
17.如图1,四边形,,,,,.
(1)求四边形的面积;
(2)如图2,以为坐标原点,以、所在直线为轴、轴建立直角坐标系,点在轴上,若,求的坐标.
18.我们规定,三角形任意两边的“广益值”等于第三边上的中线和这边一半的平方差.如图1,在中,是边上的中线,与的“广益值”就等于的值,可记为
(1)在中,若,,求的值.
(2)如图2,在中,,,求,的值.
(3)如图3,在中,是边上的中线,,,,求和的长.
19.如图,一块形如四边形ABCD的草地中,AB=3m,BC=4m,CD=12m,DA=13m,且∠ABC=90°,要以AC、CD、DA为边制作围栏,问围栏长多少米,草地面积多大?
20.为了庆祝红宝石婚纪念日,詹克和凯丽全家举行聚会.詹克忽然发现他的年龄的平方与凯丽年龄的平方的差,正好等于他的子女数目的平方,已知詹克比凯丽大一岁,现在他们都不到70岁.请问,当年结婚时,两个人各是多少岁?现在共有子女几人?(在西方,结婚40周年被称为红宝石婚,且该国的合法结婚年龄为16岁)
21.如图,中,∠C=90°,,,若动点P从点C开始,按的路径运动,且速度为每秒1cm,设出发的时间为t秒.
点P出发2秒后,求CP和BP的长.
问t满足什么条件时的值或取值范围,为直角三角形?
另有一点Q,从点C开始,按的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动当t为何值时,直线PQ把的周长分成相等的两部分?
22.已知,如图所示,四边形中,,,,,,求四边形的面积.
23.(1)如图1,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.请按要求画图:将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接BB′,则∠AB′B=
;
(2)如图2,在等边三角形ABC内有一点P,且PA=,PB=2,PC=,求∠BPC的度数和等边三角形ABC的边长;
(3)如图3,在正方形ABCD内有一点P,且PA=,PB=2,PC=,求∠BPC的度数和正方形ABCD的边长.
【参考答案】
1.C
2.B
3.C
4.A
5.D
6.C
7.B
8.D
9.B
10.B
11.45°.
12.45
13.17,144,145
14.
15.7
16.(1)点M、N是线段AB的勾股分割点;(2)或.
17.(1)36;(2)(0,0)或(0,8)
18.(1)AC=9;(2)ABAC=-72,BABC=216;(3)BC=2OC=2,AB=10.
19.24m2.
20.詹克21岁,凯丽20岁,现在共有11个子女.
21.(1)PB=cm;CP=2cm;(2)或;(3)或6秒.
22.
23.(1)见解析,45°;(2)∠BPC=150°,等边三角形ABC的边长为;(3)∠BPC=135°,正方形ABCD的边长为.
第十七章
勾股定理
17.2
勾股定理的逆定理
课后练习2
一、选择题
1.在中,、、的对应边分别是a、b、c,下列条件中不能说明是直角三角形的是(
)
A.
B.
C.
D.
2.下列条件能使(a,b,c为的三边长)为直角三角形的是(
)
A.
B.
C.
D.
3.如图,在的正方形网格中,的度数是(
)
A.22.5°
B.30°
C.45°
D.60°
4.在中,是直线上一点,已知,,,,则的长为(
)
A.4或14
B.10或14
C.14
D.10
5.△ABC的三边的长a、b、c满足:,则△ABC的形状为(
).
A.等腰三角形
B.等边三角形
C.钝角三角形
D.直角三角形
6.如图,已知中,的垂直平分线分别交于连接,则的长为(
)
A.
B.
C.
D.
7.中,,,BC边上中线,则AB,AC关系为
A.
B.
C.
D.无法确定
8.已知的三边长分别为a,b,c,且这三边长满足,则最长边上的高h=()
A.3
B.4
C.5
D.
9.下列三角形中,是直角三角形的是(
).
A.三角形的三边满足关系a+b=c
B.三角形的三边为9,40,41
C.三角形的一边等于另一边的一半
D.三角形的三边比为1∶2∶3
10.已知三角形的三边长分别为a,b,c,且a+b=10,ab=18,c=8,则该三角形的形状是(
)
A.等腰三角形
B.直角三角形
C.钝角三角形
D.等腰直角三角形
二、填空题
11.在△ABC中,AC=BC=,AB=2,则△ABC中的最小角是_____.
12.如图所示的网格是正方形网格,则__________°(点,,是网格线交点).
13.观察:①3、4、5,②5、12、13,③7、24、25,……,发现这些勾股数的“勾”都是奇数,且从3起就没断过.根据以上规律,请写出第8组勾股数:______.
14.如图,在中,是边中点,,,则的长是_____________.
15.如图,P为正三角形ABC内一点,PA=2,PB=4,PC=2,则正三角形ABC的面积为_____.
三、解答题
16.定义:如图,点M、N把线段AB分割成AM、MN、NB,若以AM、MN、NB为边的三角形是一个直角三角形,则称点M、N是线段AB的勾股分割点.
(1)已知M、N把线段分割成AM、MN、NB,若,,,则点M、N是线段AB的勾股分割点吗?请说明理由.
(2)已知M、N是线段AB的勾股分割点,且AM为直角边,若AB=12,AM=5,求BN的长.
17.如图1,四边形,,,,,.
(1)求四边形的面积;
(2)如图2,以为坐标原点,以、所在直线为轴、轴建立直角坐标系,点在轴上,若,求的坐标.
18.我们规定,三角形任意两边的“广益值”等于第三边上的中线和这边一半的平方差.如图1,在中,是边上的中线,与的“广益值”就等于的值,可记为
(1)在中,若,,求的值.
(2)如图2,在中,,,求,的值.
(3)如图3,在中,是边上的中线,,,,求和的长.
19.如图,一块形如四边形ABCD的草地中,AB=3m,BC=4m,CD=12m,DA=13m,且∠ABC=90°,要以AC、CD、DA为边制作围栏,问围栏长多少米,草地面积多大?
20.为了庆祝红宝石婚纪念日,詹克和凯丽全家举行聚会.詹克忽然发现他的年龄的平方与凯丽年龄的平方的差,正好等于他的子女数目的平方,已知詹克比凯丽大一岁,现在他们都不到70岁.请问,当年结婚时,两个人各是多少岁?现在共有子女几人?(在西方,结婚40周年被称为红宝石婚,且该国的合法结婚年龄为16岁)
21.如图,中,∠C=90°,,,若动点P从点C开始,按的路径运动,且速度为每秒1cm,设出发的时间为t秒.
点P出发2秒后,求CP和BP的长.
问t满足什么条件时的值或取值范围,为直角三角形?
另有一点Q,从点C开始,按的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动当t为何值时,直线PQ把的周长分成相等的两部分?
22.已知,如图所示,四边形中,,,,,,求四边形的面积.
23.(1)如图1,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.请按要求画图:将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接BB′,则∠AB′B=
;
(2)如图2,在等边三角形ABC内有一点P,且PA=,PB=2,PC=,求∠BPC的度数和等边三角形ABC的边长;
(3)如图3,在正方形ABCD内有一点P,且PA=,PB=2,PC=,求∠BPC的度数和正方形ABCD的边长.
【参考答案】
1.C
2.B
3.C
4.A
5.D
6.C
7.B
8.D
9.B
10.B
11.45°.
12.45
13.17,144,145
14.
15.7
16.(1)点M、N是线段AB的勾股分割点;(2)或.
17.(1)36;(2)(0,0)或(0,8)
18.(1)AC=9;(2)ABAC=-72,BABC=216;(3)BC=2OC=2,AB=10.
19.24m2.
20.詹克21岁,凯丽20岁,现在共有11个子女.
21.(1)PB=cm;CP=2cm;(2)或;(3)或6秒.
22.
23.(1)见解析,45°;(2)∠BPC=150°,等边三角形ABC的边长为;(3)∠BPC=135°,正方形ABCD的边长为.
