4.3.3 余角和补角(1)
文档属性
| 名称 | 4.3.3 余角和补角(1) |

|
|
| 格式 | rar | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-22 14:19:37 | ||
图片预览











文档简介
(共35张PPT)
第四章 图形认识初步
4.3 角
重庆市开县西街中学 罗堂喜
4.3.3 余角和补角(1)
创设情境,引出新知
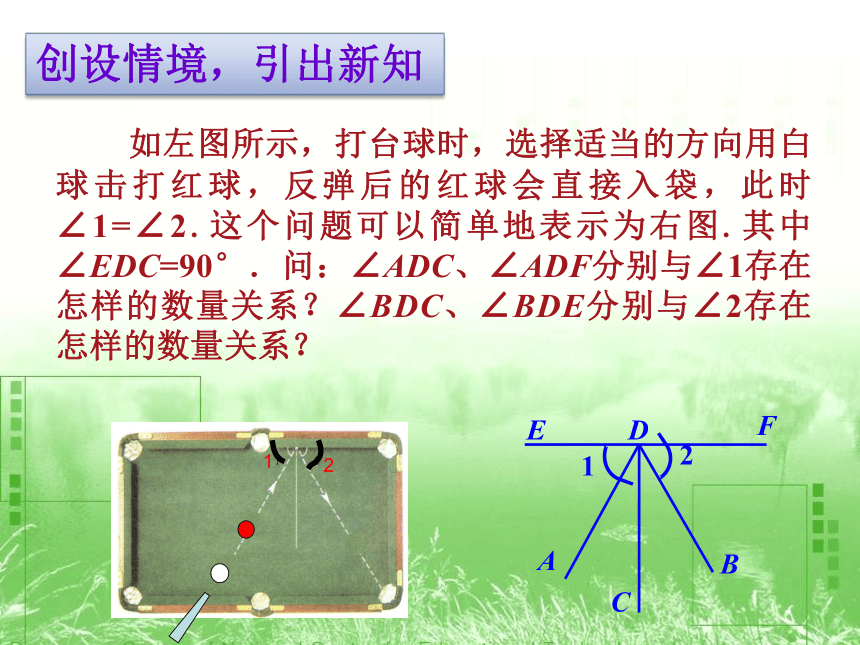
如左图所示,打台球时,选择适当的方向用白球击打红球,反弹后的红球会直接入袋,此时∠1=∠2.这个问题可以简单地表示为右图.其中∠EDC=90°.问:∠ADC、∠ADF分别与∠1存在怎样的数量关系?∠BDC、∠BDE分别与∠2存在怎样的数量关系?
1
2
E
D
A
C
B
F
1
2
1
2
∠1和∠2有什么关系?
一、互为余角,互为补角
如果两个角的和是一个直角(或等于90°),那么这两个角叫做互为余角,其中一个角是另一个角的余角。
2
1
∵∠1+∠2=90°,
∴∠1和∠2互为余角。
图中给出的各角,那些互为余角?
10o
30o
60o
80o
50o
40o
3
4
∠3和∠4有什么关系?
3
4
互为补角
如果两个角的和是一个平角(或等于180°),那么这两个角叫做互为补角,其中一个角是另一个角的补角。
∵∠3+∠4=180°,∴∠3和∠4互为补角。
1.图中给出的各角,那些互为补角?
10o
30o
60o
80o
100o
120o
150o
170o
2. 若一个角的补角等于它的余角的4 倍, 求这个角的度数。
解: 设这个角是x °,则它的补角是 ( 180°-x°),余角是(90°-x°) 。
根据题意得:
(180°-x°)= 4 (90°-x°)
解得: x =60
答:这个角的度数是60 °。
1.定义中的“互为”是什么意思?
2.把上图中∠1与∠ADF分离并多次变换位置,如图,这两角还是互为补角吗?
理解定义,巩固运用
1
A
D
F
1
1
理解定义,巩固运用
(1)若∠1与∠2互补,则∠1+ ∠2=______.
(2) ∠1=90°- ∠2,则∠1与∠2的关系为___________.
180°
互为余角
角α α的余角 α的补角
9°
62°
32°33′
71°3′18″
x
28°
81°
171°
118°
57°27′
147°27′
18°56′42″
108°56′42″
(3)填表:
90°- x
180°- x
∠DOC
∠BOD
∠AOC
(4)如图,O是直线AB上点,OC是∠AOB平分线,OD是任意一条射线,
则∠AOD的补角是___________,
余角是 ,
∠COB的补角是 .
(5)一个锐角的补角比这个角的余角大多少度?
(6)一个角比它的余角大25°,求这个角的度数.
(7)互余且相等的两个角,各是多少度?
活学活用.加深理解
1、90度的角叫余角,180度的角叫补角。 ( )
2、若∠1+∠2+∠3=90°,则∠1,∠2,∠3互为余角 。( )
3、如果一个角有补角,那么这个角一定是钝角。( )
4、互补的两个角不可能相等。 ( )
5、钝角没有余角,但一定有补角。( )
6、互余的两个角一定都是锐角,两个锐角一定互余.( )
7、如果∠A=25°,∠B=75°,那么∠A与∠B互余。( )
8、如果∠A=x°,∠B=(90-x)°,那么∠A与∠B互余。( )
一、判断题:
随堂练习
如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
1
2
4
3
答:∠2与∠4相等。
∠4=90°-∠3
∴ ∠2 =∠4
∵ ∠1 与∠2互余,
∵ ∠3与∠4互余 ,∴
∵ ∠1 =∠3,
理由如下:
探究1
这里用到了: 等量减等量,差相等
∴ ∠2=90°-∠1 ,
二、余角和补角的性质
余角的性质
等角(同角)的余角相等
例 如图∠AOC= ∠BOC=∠DOE=90°,则
图中与∠3互余的角是_________,
图中与∠4互余的角是_________,
图中有与∠3互补的角吗 _________.
图中有哪些角相等?
∠2,
∠4
∠3,
∠1
∠BOD
∠1=∠3,∠2=∠4
如图∠1 与∠2互补,∠3 与∠4互补 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
1
3
2
4
1
4
3
2
探究2
答:∠2 =∠4 ,因为 ∠1 =∠3,所以180°- ∠1 =180°- ∠3(等量减等量差相等)
补角性质
(2)已知∠1与∠2互补, ∠3也与∠2互补.那么∠1和∠3 相等吗?为什么
推导性质,理解运用
补角性质
等角(同角)的补角相等
等角 的余角相等.
归纳
等角 的补角相等.
对于余角是否也有类似性质?
(同角)
(同角)
请认真观察下图,回答下列问题:
(2)图中哪几对角是相等的角(直角除外)?为什么?
(1)图中有哪几对互余的角?
∠A+∠B=90° ∠A+∠2=90°
∠1+∠B=90° ∠1+∠2=90°
∠B=∠2
∠A=∠1
B
A
C
D
1
2
(同角的余角相等)
(同角的余角相等)
随堂练习
中考链接
1
1.(2010.山东临沂)如果∠a=60° ,那么∠a的余角的度数是( )
A.30° B.60° C.90° D.120°
2.(2009.宁德市)如图,已知直线AB、CD相交于点O,OE平分∠COB,若∠EOB=55 ,则∠BOD的度数是( )
A.35 B.55 C.70 D.110
A
C
(3)如果一个角的余角和补角都存在,那么这
个角的余角一定比这个角的补角小.
(2)如果两个角互补,那么这两个角中,一个
是锐角,另一个是钝角;
(1)一个锐角的补角一定是钝角;
1、判断下列说法是否正确,并说明理由.
√
√
注意:1、只有锐角有余角;
2、一个角的余角与它的补角相差90°.
还少20°,
求这个角的度数。
设这个角为x,则90-x+20= (180-x),x=75°
2.一个角的余角比它的补角的
(1)若∠1与∠2互余,∠2与∠3互余, 则_____=______,根据是________ .
若∠3与∠4互补,∠6与∠5互补,且∠3=∠6, 则_____=______,根据是________.
同角的余角相等
∠1
∠3
∠4
∠5
推导性质,理解运用
等角的补
角相等
(2) 如图,A、O、 B在同一直线上,∠AOC= ∠DOE=90°,找出图中互余的角、相等的角、互补的角.
推导性质,理解运用
推导性质,理解运用
互余的角是:
∠AOD和 ∠DOC,
∠DOC 和∠COE,
∠COE和 ∠EOB.
互补的角是:
∠AOD和 ∠DOB,
相等的角是:
∠AOD=∠COE,
∠DOC =∠EOB,
∠AOC= ∠BOC= ∠DOE.
∠COE和 ∠DOB,
∠AOC和∠BOC,
∠AOC和∠DOE,
∠BOC和∠DOE,
∠AOE和 ∠EOB,
∠AOE和 ∠DOC.
∠AOD和 ∠EOB.
互为余角 互为补角
对应图形
数量关系
性 质
课堂小结,自我完善
1
2
1
2
∠1+ ∠2 = 90 °
∠1+ ∠2 = 180 °
等角或同角的余角相等
等角或同角的补角相等
拓展延伸,布置作业
1.教科书第144页习题4.3第 7、8题.
2.一个角的余角比
这个角的补角的
多6°,求这个角.
拓展延伸,布置作业
3.(选做题)一个角的余角比这个角的补角的
还小10°,求这个角的余角及这个角的补角的度数.(用两种方法求解)
1、互为余角(互余)、互为补角(互补)是两个角之间的数量关系,不是位置关系。
2、互为余角的两个角不一定是直角中分成的两个角,互为补角的两个角不一定是平角中分成的两个角。
3、同一个角的补角比余角大90度。
小结归纳
1
二、填空。
如图,OD平分∠COA ,OE平分∠COB,则①∠ EOD=__ °
②图中互余角有 对, 互补角有 对。
90
4
5
D
E
O
C
A
B
点滴收获
● 本节课你学到了哪些知识?
● 通过这节课的学习后,你有什么感受
第四章 图形认识初步
4.3 角
重庆市开县西街中学 罗堂喜
4.3.3 余角和补角(1)
创设情境,引出新知
如左图所示,打台球时,选择适当的方向用白球击打红球,反弹后的红球会直接入袋,此时∠1=∠2.这个问题可以简单地表示为右图.其中∠EDC=90°.问:∠ADC、∠ADF分别与∠1存在怎样的数量关系?∠BDC、∠BDE分别与∠2存在怎样的数量关系?
1
2
E
D
A
C
B
F
1
2
1
2
∠1和∠2有什么关系?
一、互为余角,互为补角
如果两个角的和是一个直角(或等于90°),那么这两个角叫做互为余角,其中一个角是另一个角的余角。
2
1
∵∠1+∠2=90°,
∴∠1和∠2互为余角。
图中给出的各角,那些互为余角?
10o
30o
60o
80o
50o
40o
3
4
∠3和∠4有什么关系?
3
4
互为补角
如果两个角的和是一个平角(或等于180°),那么这两个角叫做互为补角,其中一个角是另一个角的补角。
∵∠3+∠4=180°,∴∠3和∠4互为补角。
1.图中给出的各角,那些互为补角?
10o
30o
60o
80o
100o
120o
150o
170o
2. 若一个角的补角等于它的余角的4 倍, 求这个角的度数。
解: 设这个角是x °,则它的补角是 ( 180°-x°),余角是(90°-x°) 。
根据题意得:
(180°-x°)= 4 (90°-x°)
解得: x =60
答:这个角的度数是60 °。
1.定义中的“互为”是什么意思?
2.把上图中∠1与∠ADF分离并多次变换位置,如图,这两角还是互为补角吗?
理解定义,巩固运用
1
A
D
F
1
1
理解定义,巩固运用
(1)若∠1与∠2互补,则∠1+ ∠2=______.
(2) ∠1=90°- ∠2,则∠1与∠2的关系为___________.
180°
互为余角
角α α的余角 α的补角
9°
62°
32°33′
71°3′18″
x
28°
81°
171°
118°
57°27′
147°27′
18°56′42″
108°56′42″
(3)填表:
90°- x
180°- x
∠DOC
∠BOD
∠AOC
(4)如图,O是直线AB上点,OC是∠AOB平分线,OD是任意一条射线,
则∠AOD的补角是___________,
余角是 ,
∠COB的补角是 .
(5)一个锐角的补角比这个角的余角大多少度?
(6)一个角比它的余角大25°,求这个角的度数.
(7)互余且相等的两个角,各是多少度?
活学活用.加深理解
1、90度的角叫余角,180度的角叫补角。 ( )
2、若∠1+∠2+∠3=90°,则∠1,∠2,∠3互为余角 。( )
3、如果一个角有补角,那么这个角一定是钝角。( )
4、互补的两个角不可能相等。 ( )
5、钝角没有余角,但一定有补角。( )
6、互余的两个角一定都是锐角,两个锐角一定互余.( )
7、如果∠A=25°,∠B=75°,那么∠A与∠B互余。( )
8、如果∠A=x°,∠B=(90-x)°,那么∠A与∠B互余。( )
一、判断题:
随堂练习
如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
1
2
4
3
答:∠2与∠4相等。
∠4=90°-∠3
∴ ∠2 =∠4
∵ ∠1 与∠2互余,
∵ ∠3与∠4互余 ,∴
∵ ∠1 =∠3,
理由如下:
探究1
这里用到了: 等量减等量,差相等
∴ ∠2=90°-∠1 ,
二、余角和补角的性质
余角的性质
等角(同角)的余角相等
例 如图∠AOC= ∠BOC=∠DOE=90°,则
图中与∠3互余的角是_________,
图中与∠4互余的角是_________,
图中有与∠3互补的角吗 _________.
图中有哪些角相等?
∠2,
∠4
∠3,
∠1
∠BOD
∠1=∠3,∠2=∠4
如图∠1 与∠2互补,∠3 与∠4互补 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
1
3
2
4
1
4
3
2
探究2
答:∠2 =∠4 ,因为 ∠1 =∠3,所以180°- ∠1 =180°- ∠3(等量减等量差相等)
补角性质
(2)已知∠1与∠2互补, ∠3也与∠2互补.那么∠1和∠3 相等吗?为什么
推导性质,理解运用
补角性质
等角(同角)的补角相等
等角 的余角相等.
归纳
等角 的补角相等.
对于余角是否也有类似性质?
(同角)
(同角)
请认真观察下图,回答下列问题:
(2)图中哪几对角是相等的角(直角除外)?为什么?
(1)图中有哪几对互余的角?
∠A+∠B=90° ∠A+∠2=90°
∠1+∠B=90° ∠1+∠2=90°
∠B=∠2
∠A=∠1
B
A
C
D
1
2
(同角的余角相等)
(同角的余角相等)
随堂练习
中考链接
1
1.(2010.山东临沂)如果∠a=60° ,那么∠a的余角的度数是( )
A.30° B.60° C.90° D.120°
2.(2009.宁德市)如图,已知直线AB、CD相交于点O,OE平分∠COB,若∠EOB=55 ,则∠BOD的度数是( )
A.35 B.55 C.70 D.110
A
C
(3)如果一个角的余角和补角都存在,那么这
个角的余角一定比这个角的补角小.
(2)如果两个角互补,那么这两个角中,一个
是锐角,另一个是钝角;
(1)一个锐角的补角一定是钝角;
1、判断下列说法是否正确,并说明理由.
√
√
注意:1、只有锐角有余角;
2、一个角的余角与它的补角相差90°.
还少20°,
求这个角的度数。
设这个角为x,则90-x+20= (180-x),x=75°
2.一个角的余角比它的补角的
(1)若∠1与∠2互余,∠2与∠3互余, 则_____=______,根据是________ .
若∠3与∠4互补,∠6与∠5互补,且∠3=∠6, 则_____=______,根据是________.
同角的余角相等
∠1
∠3
∠4
∠5
推导性质,理解运用
等角的补
角相等
(2) 如图,A、O、 B在同一直线上,∠AOC= ∠DOE=90°,找出图中互余的角、相等的角、互补的角.
推导性质,理解运用
推导性质,理解运用
互余的角是:
∠AOD和 ∠DOC,
∠DOC 和∠COE,
∠COE和 ∠EOB.
互补的角是:
∠AOD和 ∠DOB,
相等的角是:
∠AOD=∠COE,
∠DOC =∠EOB,
∠AOC= ∠BOC= ∠DOE.
∠COE和 ∠DOB,
∠AOC和∠BOC,
∠AOC和∠DOE,
∠BOC和∠DOE,
∠AOE和 ∠EOB,
∠AOE和 ∠DOC.
∠AOD和 ∠EOB.
互为余角 互为补角
对应图形
数量关系
性 质
课堂小结,自我完善
1
2
1
2
∠1+ ∠2 = 90 °
∠1+ ∠2 = 180 °
等角或同角的余角相等
等角或同角的补角相等
拓展延伸,布置作业
1.教科书第144页习题4.3第 7、8题.
2.一个角的余角比
这个角的补角的
多6°,求这个角.
拓展延伸,布置作业
3.(选做题)一个角的余角比这个角的补角的
还小10°,求这个角的余角及这个角的补角的度数.(用两种方法求解)
1、互为余角(互余)、互为补角(互补)是两个角之间的数量关系,不是位置关系。
2、互为余角的两个角不一定是直角中分成的两个角,互为补角的两个角不一定是平角中分成的两个角。
3、同一个角的补角比余角大90度。
小结归纳
1
二、填空。
如图,OD平分∠COA ,OE平分∠COB,则①∠ EOD=__ °
②图中互余角有 对, 互补角有 对。
90
4
5
D
E
O
C
A
B
点滴收获
● 本节课你学到了哪些知识?
● 通过这节课的学习后,你有什么感受
