直角三角形的三边关系
图片预览

文档简介
直角三角形的三边关系(一)
一. 正切:
定义:在Rt△ABC中,锐角∠A的对边与邻边的比叫做∠A的正切,记作tanA,即;
tanA的值越大,梯子越陡,∠A越大; ∠A越大,梯子越陡,tanA的值越大。
二. 正弦:
定义:在Rt△ABC中,锐角∠A的对边与斜边的比叫做∠A的正弦,记作sinA,即;
三. 余弦:
定义:在Rt△ABC中,锐角∠A的邻边与斜边的比叫做∠A的余弦,记作cosA,即;
四、余切:
定义:在Rt△ABC中,锐角∠A的邻边与对边的比叫做∠A的余切,记作cotA,即;
五、一个锐角的正弦、余弦、正切、余切分别等于它的余角的余弦、正弦、余切、正切。
0 30 45 60 90
sinα 0 1
cosα 1 0
tanα 0 1 —
cotα — 1 0
(通常我们称正弦、余弦互为余函数。同样,也称正切、余切互为余函数,可以概括为:一个锐角的三角函数等于它的余角的余函数)用等式表达:若∠A为锐角,则
①;
②;
六、当从低处观测高处的目标时,视线与水平线
所成的锐角称为仰角
当从高处观测低处的目标时,视线与水平线所成
的锐角称为俯角
七、利用特殊角的三角函数值表,可以看出,(1)当
角度在0°~90°间变化时,正弦值、正切值随着角度的增大(或减小)而增大(或减小);余弦值、余切值随着角度的增大(或减小)而减小(或增大)。(2)0≤sinα≤1,0≤cosα≤1。
※同角的三角函数间的关系:
倒数关系:tgα·ctgα=1。
八、在直角三角形中,除直角外,一共有五个元素,即三条边和二个锐角。由直角三角形中除直角外的已知元素,求出所有未知元素的过程,叫做解直角三角形。
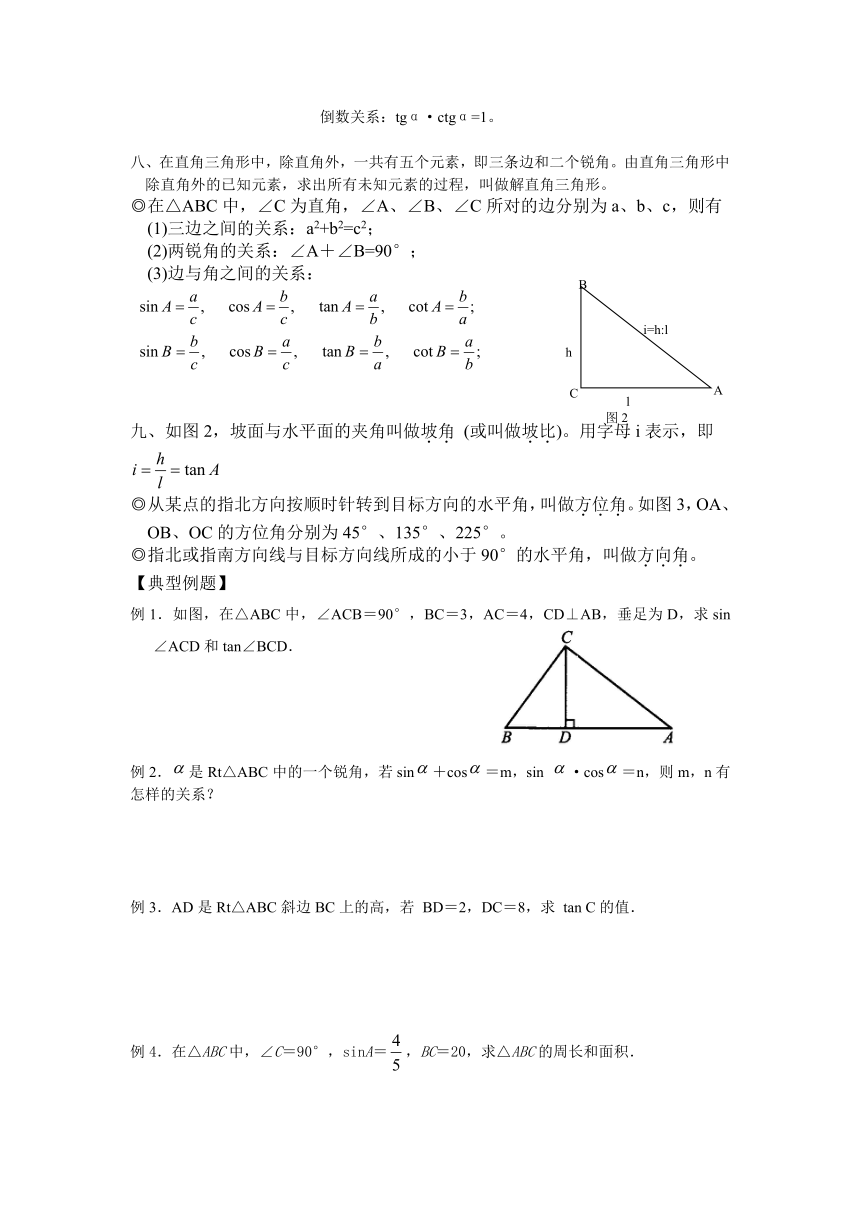
◎在△ABC中,∠C为直角,∠A、∠B、∠C所对的边分别为a、b、c,则有
(1)三边之间的关系:a2+b2=c2;
(2)两锐角的关系:∠A+∠B=90°;
(3)边与角之间的关系:
九、如图2,坡面与水平面的夹角叫做坡角 (或叫做坡比)。用字母i表示,即
◎从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角。如图3,OA、OB、OC的方位角分别为45°、135°、225°。
◎指北或指南方向线与目标方向线所成的小于90°的水平角,叫做方向角。
【典型例题】
例1.如图,在△ABC中,∠ACB=90°,BC=3,AC=4,CD⊥AB,垂足为D,求sin∠ACD和tan∠BCD.
例2.是Rt△ABC中的一个锐角,若sin+cos=m,sin ·cos=n,则m,n有怎样的关系?
例3.AD是Rt△ABC斜边BC上的高,若 BD=2,DC=8,求 tan C的值.
例4.在△ABC中,∠C=90°,sinA=,BC=20,求△ABC的周长和面积.
例5.已知:如图,CD是Rt△ABC的斜边AB上的高,求证:BC2=AB·BD.
(用正弦、余弦函数的定义证明)
一:选择题
1.若△ABC中,∠C=90°,则cosA的值等于 ( )
2.若锐角α>β,则 ( )
A.cosα>cosβ; B.sinα<sinβ;
C.sinα>cosβ; D.sinα>sinβ.
4.α锐角,则|sinα-1|等于( )
A.1-sinα; B.sinα-1; C.cosα; D.无法确定.
5.在△ABC中,∠C=90°,AC=BC,则tanA等于( )
6.若α为锐角且tanα=cot42°,则α为 ( )
A.42°; B.48°; C.56°; D.无法确定.
7下列各式中错误的是( )
8.已知在△ABC中,∠C=90°,则下列各式中正确的是( )
A.sinA=sinB; B.cosA=cosB C.tanA=tanB D.tanA=cotB.
二.解答题
9.tan10°·tan20°·tan30°·tan40°·tan50°·tan60°·tan70°·tan80°.
10.sin231°+tan31°·tan59°+sin259°
的度数.
14.已知三角形三边的比是25∶24∶7,求最小角的余弦值和正切值.
15、.已知为一锐角,sin=,求 cos,tan.
16、.如图,在△ABC中,∠ACB=90°,BC=3,AC=4,CD⊥AB,
垂足为D,求sin∠ACD和tan∠BCD.
17、.在△ABC中,∠C=90°,BC=16 cm,AC=20 cm,求tan A和tan B的值.
18、.已知等腰三角形的一条腰长为 20 cm,底边长为 30 cm,求底角的正切值.
19、.如图,在等腰梯形 ABCD中,CD=4 cm,DE=6 cm,AB=8 cm,求 tan A的值.
20、.如图,山坡AB的坡度为5∶12,一辆汽车从山脚下A处出发,把货物运送到距山脚500 m高的B处,求汽车从A到B所行驶的路程.
图1
图2
h
i=h:l
l
A
B
C
一. 正切:
定义:在Rt△ABC中,锐角∠A的对边与邻边的比叫做∠A的正切,记作tanA,即;
tanA的值越大,梯子越陡,∠A越大; ∠A越大,梯子越陡,tanA的值越大。
二. 正弦:
定义:在Rt△ABC中,锐角∠A的对边与斜边的比叫做∠A的正弦,记作sinA,即;
三. 余弦:
定义:在Rt△ABC中,锐角∠A的邻边与斜边的比叫做∠A的余弦,记作cosA,即;
四、余切:
定义:在Rt△ABC中,锐角∠A的邻边与对边的比叫做∠A的余切,记作cotA,即;
五、一个锐角的正弦、余弦、正切、余切分别等于它的余角的余弦、正弦、余切、正切。
0 30 45 60 90
sinα 0 1
cosα 1 0
tanα 0 1 —
cotα — 1 0
(通常我们称正弦、余弦互为余函数。同样,也称正切、余切互为余函数,可以概括为:一个锐角的三角函数等于它的余角的余函数)用等式表达:若∠A为锐角,则
①;
②;
六、当从低处观测高处的目标时,视线与水平线
所成的锐角称为仰角
当从高处观测低处的目标时,视线与水平线所成
的锐角称为俯角
七、利用特殊角的三角函数值表,可以看出,(1)当
角度在0°~90°间变化时,正弦值、正切值随着角度的增大(或减小)而增大(或减小);余弦值、余切值随着角度的增大(或减小)而减小(或增大)。(2)0≤sinα≤1,0≤cosα≤1。
※同角的三角函数间的关系:
倒数关系:tgα·ctgα=1。
八、在直角三角形中,除直角外,一共有五个元素,即三条边和二个锐角。由直角三角形中除直角外的已知元素,求出所有未知元素的过程,叫做解直角三角形。
◎在△ABC中,∠C为直角,∠A、∠B、∠C所对的边分别为a、b、c,则有
(1)三边之间的关系:a2+b2=c2;
(2)两锐角的关系:∠A+∠B=90°;
(3)边与角之间的关系:
九、如图2,坡面与水平面的夹角叫做坡角 (或叫做坡比)。用字母i表示,即
◎从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角。如图3,OA、OB、OC的方位角分别为45°、135°、225°。
◎指北或指南方向线与目标方向线所成的小于90°的水平角,叫做方向角。
【典型例题】
例1.如图,在△ABC中,∠ACB=90°,BC=3,AC=4,CD⊥AB,垂足为D,求sin∠ACD和tan∠BCD.
例2.是Rt△ABC中的一个锐角,若sin+cos=m,sin ·cos=n,则m,n有怎样的关系?
例3.AD是Rt△ABC斜边BC上的高,若 BD=2,DC=8,求 tan C的值.
例4.在△ABC中,∠C=90°,sinA=,BC=20,求△ABC的周长和面积.
例5.已知:如图,CD是Rt△ABC的斜边AB上的高,求证:BC2=AB·BD.
(用正弦、余弦函数的定义证明)
一:选择题
1.若△ABC中,∠C=90°,则cosA的值等于 ( )
2.若锐角α>β,则 ( )
A.cosα>cosβ; B.sinα<sinβ;
C.sinα>cosβ; D.sinα>sinβ.
4.α锐角,则|sinα-1|等于( )
A.1-sinα; B.sinα-1; C.cosα; D.无法确定.
5.在△ABC中,∠C=90°,AC=BC,则tanA等于( )
6.若α为锐角且tanα=cot42°,则α为 ( )
A.42°; B.48°; C.56°; D.无法确定.
7下列各式中错误的是( )
8.已知在△ABC中,∠C=90°,则下列各式中正确的是( )
A.sinA=sinB; B.cosA=cosB C.tanA=tanB D.tanA=cotB.
二.解答题
9.tan10°·tan20°·tan30°·tan40°·tan50°·tan60°·tan70°·tan80°.
10.sin231°+tan31°·tan59°+sin259°
的度数.
14.已知三角形三边的比是25∶24∶7,求最小角的余弦值和正切值.
15、.已知为一锐角,sin=,求 cos,tan.
16、.如图,在△ABC中,∠ACB=90°,BC=3,AC=4,CD⊥AB,
垂足为D,求sin∠ACD和tan∠BCD.
17、.在△ABC中,∠C=90°,BC=16 cm,AC=20 cm,求tan A和tan B的值.
18、.已知等腰三角形的一条腰长为 20 cm,底边长为 30 cm,求底角的正切值.
19、.如图,在等腰梯形 ABCD中,CD=4 cm,DE=6 cm,AB=8 cm,求 tan A的值.
20、.如图,山坡AB的坡度为5∶12,一辆汽车从山脚下A处出发,把货物运送到距山脚500 m高的B处,求汽车从A到B所行驶的路程.
图1
图2
h
i=h:l
l
A
B
C
