2020-2021学年沪科版七年级数学下册课件-10.4 平移(15张)
文档属性
| 名称 | 2020-2021学年沪科版七年级数学下册课件-10.4 平移(15张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 196.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-21 00:00:00 | ||
图片预览





文档简介
10.4 平移
1.对顶角: 两条直线相交所构成的四个角中,满足条件:
1
2
3
4
相交线
(1)有公共顶点;
(2)它们的两边分别互为反向延长线.
这样的两个角叫做对顶角.
下图中的哪些角分别是对顶角?
一、对顶角
下列各图中标出来的两个角是对顶角吗?若不是,请说明理由.
2. 对顶角的性质:对顶角相等.
想一想:
n(n为不小于2的整数)条直线交于一点,形成多少对对顶角?
n(n-1)对
A
O
B
C
D
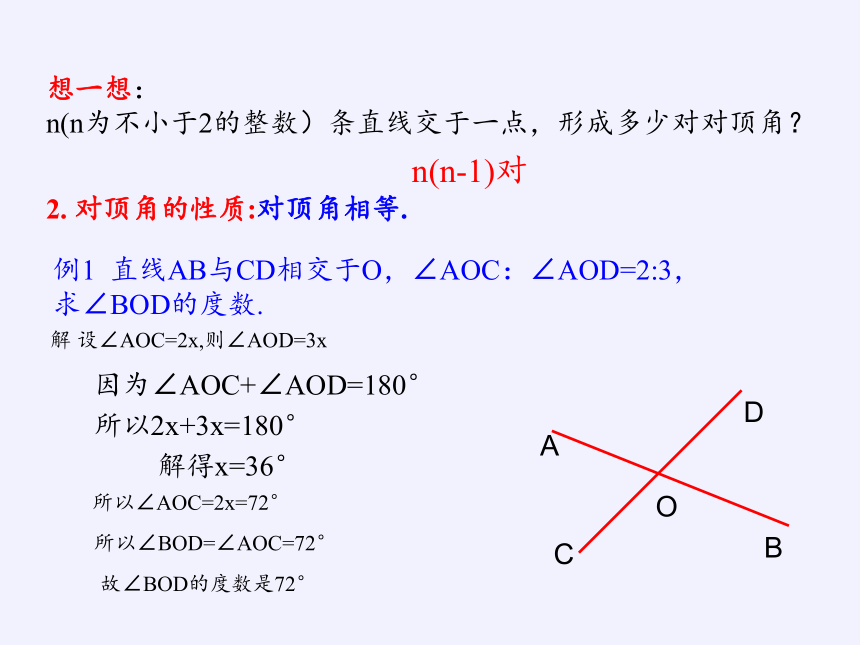
解 设∠AOC=2x,则∠AOD=3x
因为∠AOC+∠AOD=180°
所以2x+3x=180°
解得x=36°
所以∠AOC=2x=72°
所以∠BOD=∠AOC=72°
故∠BOD的度数是72°
例1 直线AB与CD相交于O,∠AOC:∠AOD=2:3,
求∠BOD的度数.
1.垂线的定义: 两条直线相交,所成的四个角中,如果有一个角是直角时,就说这两条直线互相垂直.其中一条直线叫做另一条直线的垂线.它们的交点叫垂足.
2. 垂线的性质:
(1)过一点有且只有一条直线垂直于已知直线.(存在性和唯一性)
3.点到直线的距离: 直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
二、垂线
AB⊥CD
(2)在连接直线外一点与直线上各点的线段中,垂线段最短.
O
A
C
B
D
E
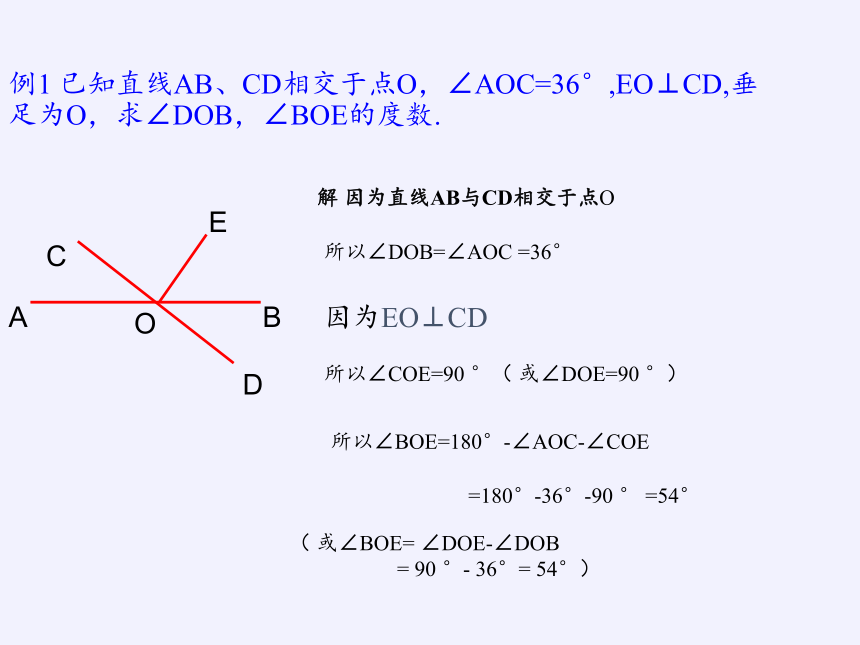
例1 已知直线AB、CD相交于点O,∠AOC=36°,EO⊥CD,垂足为O,求∠DOB,∠BOE的度数.
解 因为直线AB与CD相交于点O
所以∠DOB=∠AOC =36°
因为EO⊥CD
所以∠BOE=180°-∠AOC-∠COE
=180°-36°-90 ° =54°
所以∠COE=90 °( 或∠DOE=90 °)
( 或∠BOE= ∠DOE-∠DOB
= 90 °- 36°= 54°)
C
∟
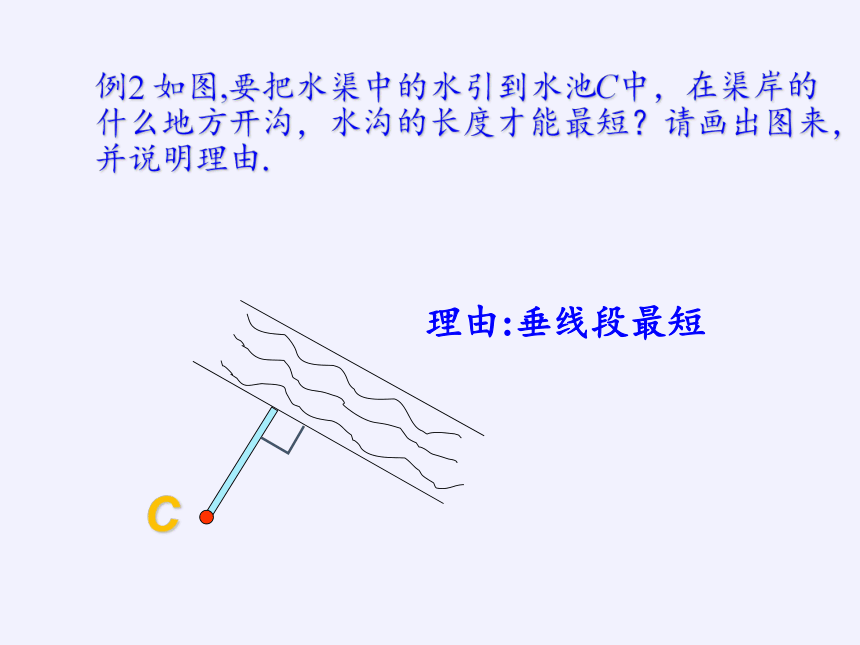
理由:垂线段最短
例2 如图,要把水渠中的水引到水池C中,在渠岸的什么地方开沟,水沟的长度才能最短?请画出图来,并说明理由.
A
D
C
B
E
F
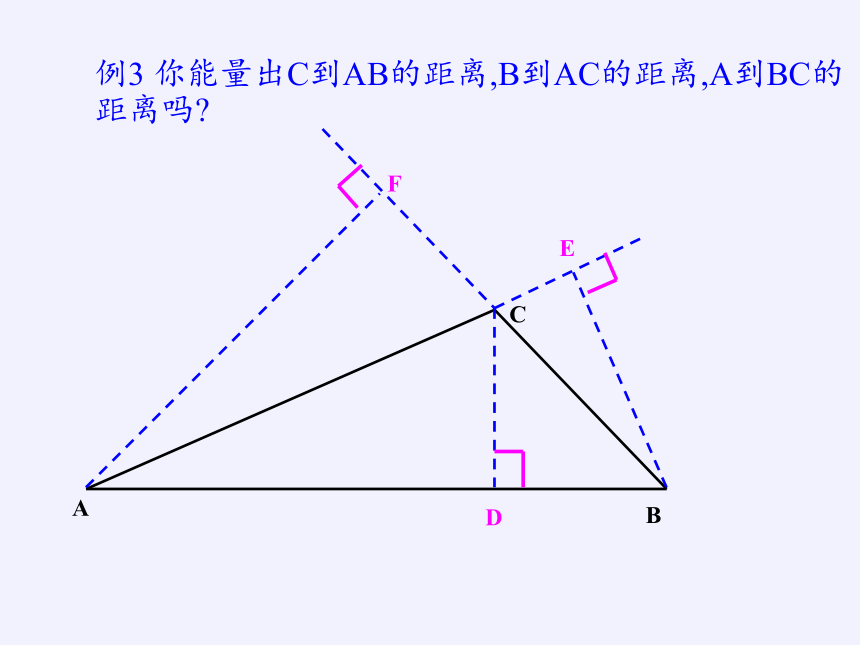
例3 你能量出C到AB的距离,B到AC的距离,A到BC的距离吗?
平行线:在同一平面内,不相交的两条直线叫做平行线.
2.平行线基本事实(存在性和唯一性)
经过直线外一点,有且只有一条直线平行于这条直线.
3.平行线的传递性 如果两条直线和第三条直线平行,那么这两条直线平行.
直线AB和CD平行,记作“AB ∥ CD”,读作“ AB平行于CD”
平行线
F
1
3
7
5
2
8
6
D
C
A
B
E
4
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
截线(直线EF)
被截线(直线AB与CD)
结构特征
同位角
同旁
同侧
F(正反或倒置)
内错角
两旁
之间(交错)
Z(或反置)
同旁内角
同旁
之间
U
4.同位角、内错角、同旁内角
5.平行线的三种角判定方法
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
填空
练 一 练
1.看图填空
(1)直线AB与CD被直线CE所截,与∠1成内错角的是 ,与∠1成同旁内角的是 .
(2)直线AB与CD被直线DE所截,与∠2成内错角的是 ,与∠2成同旁内角的是 .
(3)如果∠2= ∠6,那么 ∥ .
A
B
C
D
E
1
2
3
4
5
6
又因为∠1+∠2=180
4
1
2
3
A
B
C
E
F
D
证明 因为∠1=∠3
∠2=∠4
所以∠3+∠4=180°
所以AB//CD .
例 如图 已知:∠1+∠2=180°.
求证:AB∥CD.
6.平行线的性质
性质1 两直线平行,同位角相等.
性质2 两直线平行,内错角相等.
性质3 两直线平行,同旁内角互补.
例 如图,已知BD⊥AC,EF⊥AC,垂足分别为D、F.
求证∠1= ∠2.
证明 因为BD⊥AC,EF⊥AC
所以∠3=∠4=90O
所以EF∥BD
所以∠1= ∠2
A
B
C
D
E
F
1
2
4
3
1.什么叫平移?
在平面内,一个图形沿某个方向移动一定的距离,这种图形的变换叫做平移.
原图形上一点A平移后成为点A ′ ,这样的两点叫做对应点.
2.平移的特点
平移后,连接各组对应点的线段互相平行(或在同一条直线上)且相等.
平移只改变图形的位置,不改变图形的形状和大小.
(对应角相等,对应线段相等)
决定平移的因素是平移的方向与距离.
平移
生活中的平移随处可见,下列属于平移现象的是()
A.升国旗
B.钟表指针的运动
C.风车的转动
D.开自来水龙头
练一练
如图所示,△ABC平移到△A′B′C′的位置,则点A的
对应点是____,点B的对应点是____,点C的对应点是____.
线段AB的对应线段是___________,线段BC的对应线段是
______,线段AC的对应线段是_______.∠BAC的对应
角是________,∠ABC的对应角是_________,∠ACB的
对应角是_________.△ABC的平移方向是_____________
___________________________,平移距离是_____________
________________________________.
A
B
C
A′
B′
C′
A′
B′
C′
沿着射线AA′
(或BB′,或CC′)的方向
线段AA′的长
(或线段BB′的长或线段CC′)的长
★相交线
两直线相交 对顶角——对顶角相等
垂线 存在性和唯一性
垂线段最短(点到直线的距离)
两条直线被第
三条直线所截 同位角,内错角,同旁内角
★平行线 存在性和唯一性
传递性
判定
性质
★平移 特点
布置作业
关于本章的一份试卷.
谢 谢
1.对顶角: 两条直线相交所构成的四个角中,满足条件:
1
2
3
4
相交线
(1)有公共顶点;
(2)它们的两边分别互为反向延长线.
这样的两个角叫做对顶角.
下图中的哪些角分别是对顶角?
一、对顶角
下列各图中标出来的两个角是对顶角吗?若不是,请说明理由.
2. 对顶角的性质:对顶角相等.
想一想:
n(n为不小于2的整数)条直线交于一点,形成多少对对顶角?
n(n-1)对
A
O
B
C
D
解 设∠AOC=2x,则∠AOD=3x
因为∠AOC+∠AOD=180°
所以2x+3x=180°
解得x=36°
所以∠AOC=2x=72°
所以∠BOD=∠AOC=72°
故∠BOD的度数是72°
例1 直线AB与CD相交于O,∠AOC:∠AOD=2:3,
求∠BOD的度数.
1.垂线的定义: 两条直线相交,所成的四个角中,如果有一个角是直角时,就说这两条直线互相垂直.其中一条直线叫做另一条直线的垂线.它们的交点叫垂足.
2. 垂线的性质:
(1)过一点有且只有一条直线垂直于已知直线.(存在性和唯一性)
3.点到直线的距离: 直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
二、垂线
AB⊥CD
(2)在连接直线外一点与直线上各点的线段中,垂线段最短.
O
A
C
B
D
E
例1 已知直线AB、CD相交于点O,∠AOC=36°,EO⊥CD,垂足为O,求∠DOB,∠BOE的度数.
解 因为直线AB与CD相交于点O
所以∠DOB=∠AOC =36°
因为EO⊥CD
所以∠BOE=180°-∠AOC-∠COE
=180°-36°-90 ° =54°
所以∠COE=90 °( 或∠DOE=90 °)
( 或∠BOE= ∠DOE-∠DOB
= 90 °- 36°= 54°)
C
∟
理由:垂线段最短
例2 如图,要把水渠中的水引到水池C中,在渠岸的什么地方开沟,水沟的长度才能最短?请画出图来,并说明理由.
A
D
C
B
E
F
例3 你能量出C到AB的距离,B到AC的距离,A到BC的距离吗?
平行线:在同一平面内,不相交的两条直线叫做平行线.
2.平行线基本事实(存在性和唯一性)
经过直线外一点,有且只有一条直线平行于这条直线.
3.平行线的传递性 如果两条直线和第三条直线平行,那么这两条直线平行.
直线AB和CD平行,记作“AB ∥ CD”,读作“ AB平行于CD”
平行线
F
1
3
7
5
2
8
6
D
C
A
B
E
4
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
截线(直线EF)
被截线(直线AB与CD)
结构特征
同位角
同旁
同侧
F(正反或倒置)
内错角
两旁
之间(交错)
Z(或反置)
同旁内角
同旁
之间
U
4.同位角、内错角、同旁内角
5.平行线的三种角判定方法
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
填空
练 一 练
1.看图填空
(1)直线AB与CD被直线CE所截,与∠1成内错角的是 ,与∠1成同旁内角的是 .
(2)直线AB与CD被直线DE所截,与∠2成内错角的是 ,与∠2成同旁内角的是 .
(3)如果∠2= ∠6,那么 ∥ .
A
B
C
D
E
1
2
3
4
5
6
又因为∠1+∠2=180
4
1
2
3
A
B
C
E
F
D
证明 因为∠1=∠3
∠2=∠4
所以∠3+∠4=180°
所以AB//CD .
例 如图 已知:∠1+∠2=180°.
求证:AB∥CD.
6.平行线的性质
性质1 两直线平行,同位角相等.
性质2 两直线平行,内错角相等.
性质3 两直线平行,同旁内角互补.
例 如图,已知BD⊥AC,EF⊥AC,垂足分别为D、F.
求证∠1= ∠2.
证明 因为BD⊥AC,EF⊥AC
所以∠3=∠4=90O
所以EF∥BD
所以∠1= ∠2
A
B
C
D
E
F
1
2
4
3
1.什么叫平移?
在平面内,一个图形沿某个方向移动一定的距离,这种图形的变换叫做平移.
原图形上一点A平移后成为点A ′ ,这样的两点叫做对应点.
2.平移的特点
平移后,连接各组对应点的线段互相平行(或在同一条直线上)且相等.
平移只改变图形的位置,不改变图形的形状和大小.
(对应角相等,对应线段相等)
决定平移的因素是平移的方向与距离.
平移
生活中的平移随处可见,下列属于平移现象的是()
A.升国旗
B.钟表指针的运动
C.风车的转动
D.开自来水龙头
练一练
如图所示,△ABC平移到△A′B′C′的位置,则点A的
对应点是____,点B的对应点是____,点C的对应点是____.
线段AB的对应线段是___________,线段BC的对应线段是
______,线段AC的对应线段是_______.∠BAC的对应
角是________,∠ABC的对应角是_________,∠ACB的
对应角是_________.△ABC的平移方向是_____________
___________________________,平移距离是_____________
________________________________.
A
B
C
A′
B′
C′
A′
B′
C′
沿着射线AA′
(或BB′,或CC′)的方向
线段AA′的长
(或线段BB′的长或线段CC′)的长
★相交线
两直线相交 对顶角——对顶角相等
垂线 存在性和唯一性
垂线段最短(点到直线的距离)
两条直线被第
三条直线所截 同位角,内错角,同旁内角
★平行线 存在性和唯一性
传递性
判定
性质
★平移 特点
布置作业
关于本章的一份试卷.
谢 谢
