二分法

(共13张PPT)
二分法
用二分法求方程的近似解
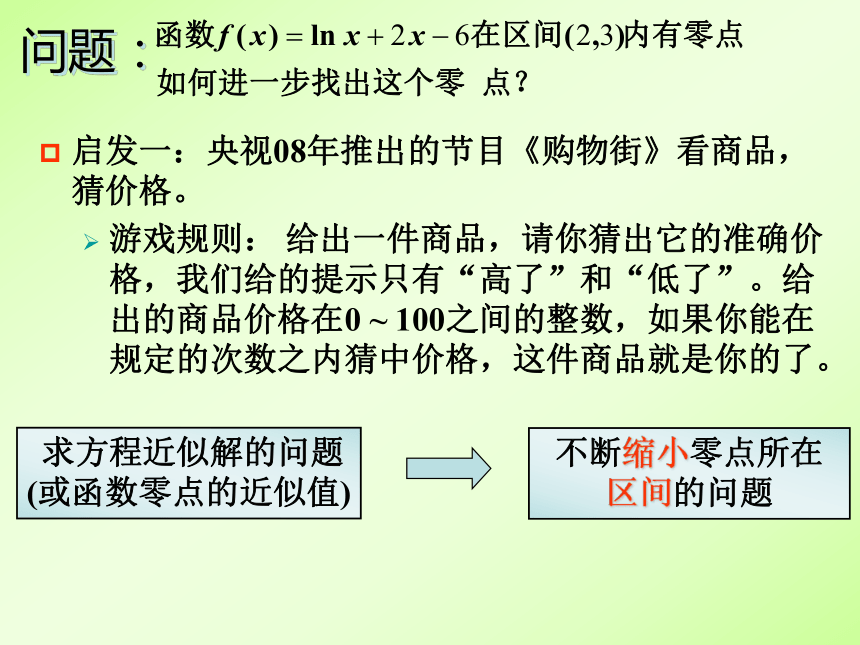
虽然指数方程、对数方程等超越方程和五次以上高次代数方程不能用代数运算求解，但其数值解法却随着现代计算技术的发展得到了广泛的运用，如二分法、牛顿法、拟牛顿法、弦截法等
问题：
启发一：央视08年推出的节目《购物街》看商品，猜价格。
游戏规则： 给出一件商品，请你猜出它的准确价格，我们给的提示只有“高了”和“低了”。给出的商品价格在0 ~ 100之间的整数，如果你能在规定的次数之内猜中价格，这件商品就是你的了。
求方程近似解的问题(或函数零点的近似值)
不断缩小零点所在 区间的问题
(3)二分法的步骤的思考
思考1:求函数f(x)的零点近似值第一步应做什么？
思考2:为了缩小零点所在区间的范围，接下来应
做什么？
思考3:若f(c)=0说明什么？若f(a)·f(c)<0或f(c)·f(b) <0 ，则分别说明什么？
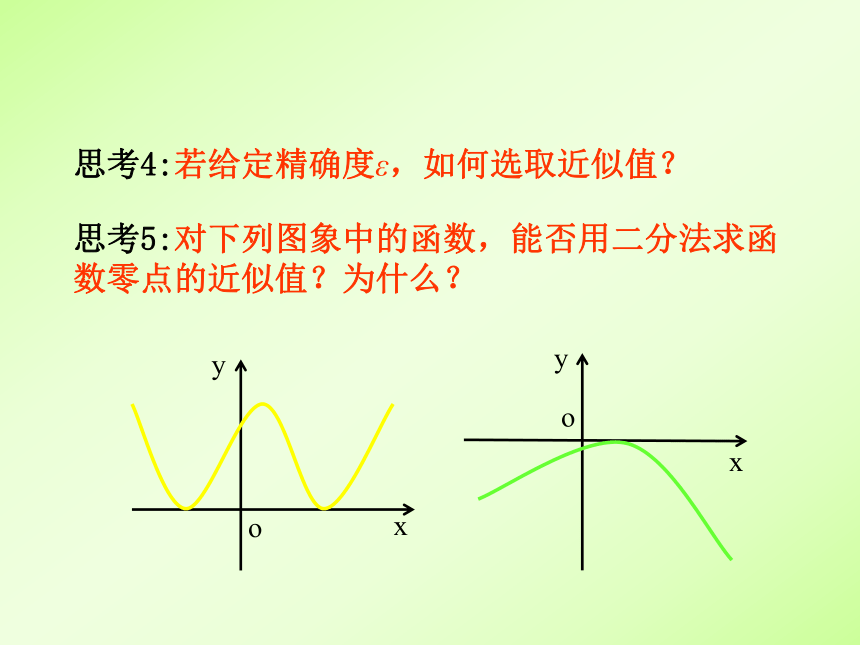
思考4:若给定精确度ε，如何选取近似值？
思考5:对下列图象中的函数，能否用二分法求函
数零点的近似值？为什么？
x
y
o
x
y
o
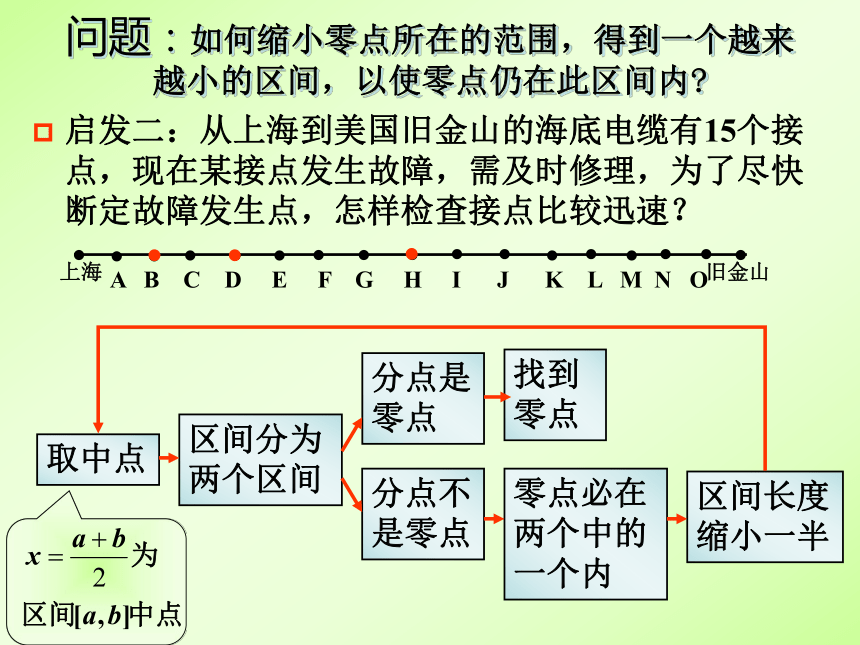
问题：如何缩小零点所在的范围，得到一个越来越小的区间，以使零点仍在此区间内
启发二：从上海到美国旧金山的海底电缆有15个接点，现在某接点发生故障，需及时修理，为了尽快断定故障发生点，怎样检查接点比较迅速？
上海
旧金山
A B C D E F G H I J K L M N O
取中点
区间分为两个区间
分点是零点
分点不是零点
零点必在两个中的一个内
区间长度缩小一半
找到零点
问题：什么时候结束？
若某次分点是零点，则结束
若分点都不是零点，需要给定精确度。
若做到(2.50，2.53)内，2.53-2.50=0.03<0.1，我们就可以得到方程的一个精确到0.1的近似解2.50
若做到(2.515，2.519)内，2.516-2.515=0.004<0.01我们就可以得到方程的一个精确到0.01的近似解 2.515
给定精确度ε：若区间长度|a-b|<ε，则得到零点的近似值a(或b)
(a,b) 中点x1 f(a) f(x1 ) f(b)
(2 , 3) 2.5 负 -0.084 正
(2.5,3) 2.75 负 0.512 正
(2.5,2.75) 2.625 负 0.215 正
(2.5,2.625) 2.5625 负 0.066 正
(2.5,2.5625) 2.53125 负 -0.009 正
(2.53125,2.5625) 2.546875 负 0.029 正
(2.53125,2.546875) 2.5390625 负 0.010 正
(2.53125,2.5390625) 2.53515625 负 0.001 正
| 2.5390625 －2.53125|=0.0078125<0.01
精确度已达到0.01
给定精确度0.01
二分法
对于在区间[a,b]上连续不断且f(a)·f(b)<0的函数y=f(x)，通过不断地把函数f(x)的零点所在的区间一分为二，使区间的两个端点逐步逼近零点，进而得到零点近似值的方法叫做二分法．
用二分法求函数零点近似值的步骤：
1．确定区间[a,b]，验证f(a)·f(b)<0，给定精确度ε
2．求区间(a,b)的中点c
3．计算f(c) (1)若f(c)=0，则c 就是函数的零点
(2)若f(a)·f(c)<0 ，则令b=c（此时零点x0∈(a,c) ）
(3)若f(c)·f(b)<0 ，则令a=c（此时零点x0∈(c,b) ）
4．判断是否达到精确度ε ：即若|a-b|<ε，则得到零点近似值a(或b)；否则重复步骤2-4．
求方程 的近似解(精确到0.1)
解
易知：f(1)<0，f(2)>0
取x=1.5，计算f(1.5)≈0.33>0
取x=1.25，计算f(1.25)≈-0.87<0
取x=1.375，计算f(1.375)≈-0.28<0
取x=1.4375，计算f(1.4375)≈0.02>0
∴ 原方程的近似解取为1.4375
运用：
1.下列图象中不能用二分法求函数的零点的是 _____
y
x
0
(C)
x
y
0
(D)
x
y
(B)
(A)
y
x
O
2. 根据表格中的数据,可以断定方程
的一个根所在的区间( )
x -1 0 1 2 3
ex 0.37 1 2.72 7.39 20.09
x+2 1 2 3 4 5
用二分法求函数f(x)在区间[1,2]上的零点（精确到0.01）的一个算法程序框图如图所示．
二次函数零点的分布（根的分布）
根的分布 x1图像
等价于