17.1.3勾股定理(第三课时 ) 课件(共17张PPT)
文档属性
| 名称 | 17.1.3勾股定理(第三课时 ) 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-21 00:00:00 | ||
图片预览



文档简介
17.1 勾股定理
第三课时 利用勾股定理表示无理数的点
第十七章 勾股定理
2021年春人教版八年级(下)数学
1.利用勾股定理画出一条线段等于已知长度为无理数的线段。
2.通过学习勾股定理的应用,培养学生基本运算能力和应用意识。
利用勾股定理画出一条线段等于已知长度为无理数的线段。(重点)
利用勾股定理解决几何问题。(难点)??
学习目标
探索与思考
八年级上册中我们曾经通过画图得到结论:斜边和一条直角边对应相等的两个直角三角形全等. 学习了勾股定理后,你能证明这一结论吗?
A
B
C
A ′
B ′
C′
已知:如图,在Rt △ABC和Rt △A ′ B ′ C ′中,
∠C= ∠C ′,AB=A ′B ′,AC=A ′C ′.
求证: △ABC ≌ △A ′ B ′ C ′.
证明:在Rt △ABC和Rt △A ′ B ′ C ′中,∠C= 90°,
根据勾股定理,得BC = ????????????????????????? , B’C’ = ????′????′?????????′????′????
又 AB = A ′B ′,AC = A ′C ′,
∴BC = B ′ C ′.
∴ △ABC ≌ △A ′ B ′ C ′(SSS).
?
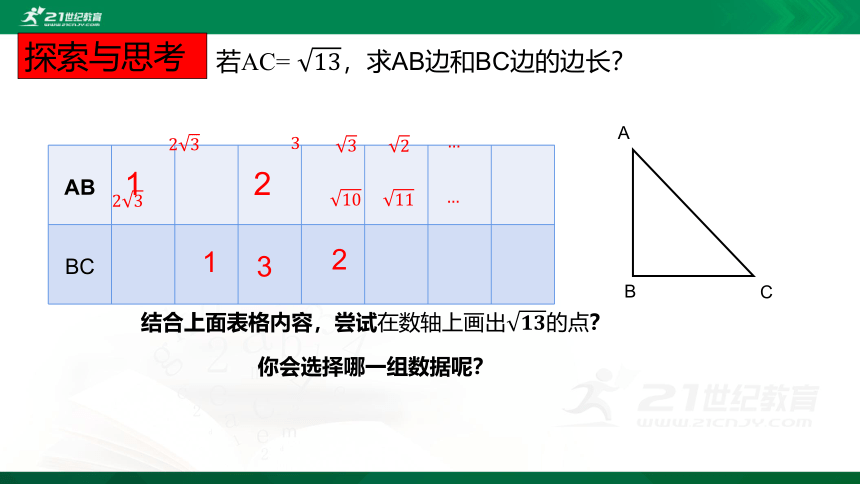
在Rt△ABC中,若AC= 13,求AB边和BC边的边长?
?
A
B
C
{69CF1AB2-1976-4502-BF36-3FF5EA218861}
AB
BC
1
23
?
1
23
?
2
3
2
3
?
3
?
10
?
2
?
11
?
…
?
…
?
结合上面表格内容,尝试在数轴上画出????????的点?
你会选择哪一组数据呢?
?
探索与思考
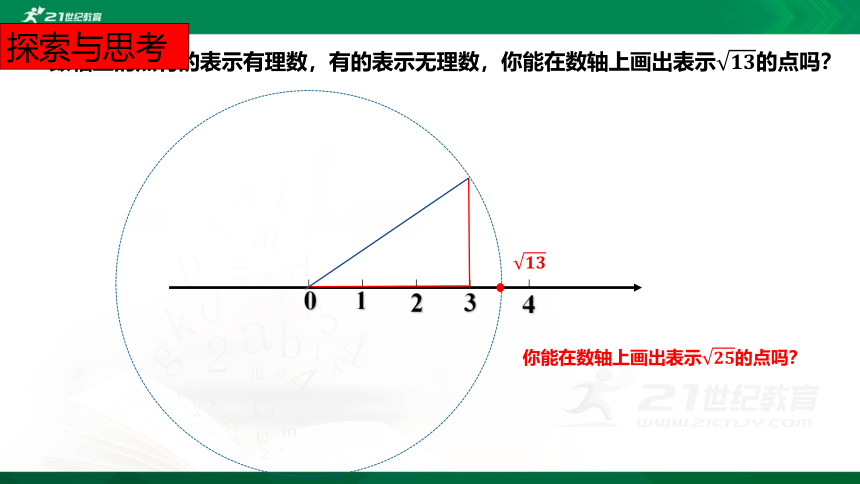
数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示????????的点吗?
?
0
1
2
3
4
????????
?
你能在数轴上画出表示????????的点吗?
?
探索与思考
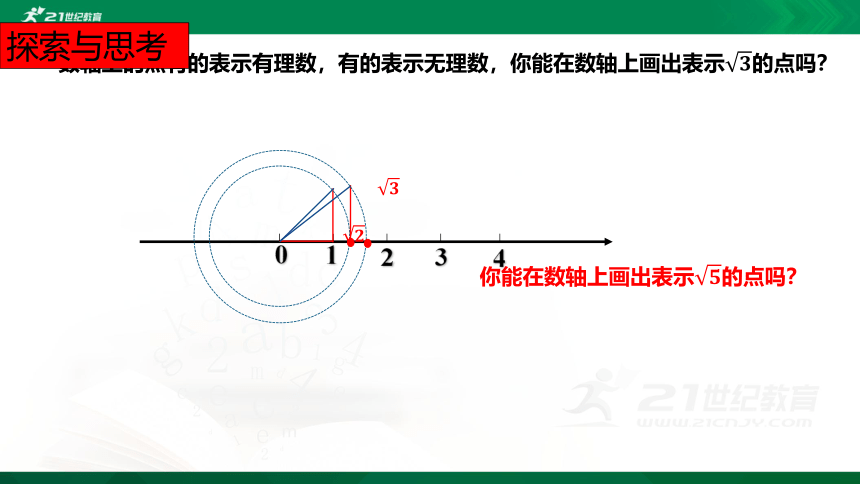
数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示????的点吗?
?
0
1
2
3
4
????
?
你能在数轴上画出表示????的点吗?
?
????
?
探索与思考
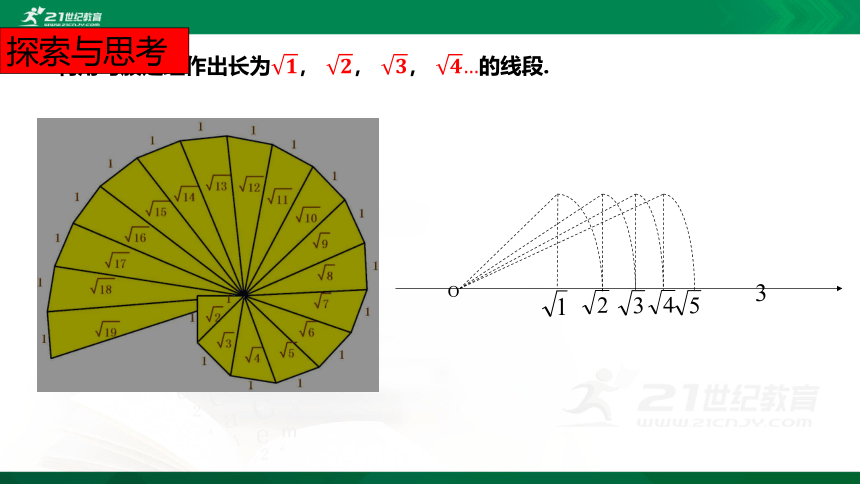
利用勾股定理作出长为????, ????, ????, ????…的线段.
?
探索与思考
O
3
1.如图,矩形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是( )
A.25 B.22 C.3 D.5
?
【答案】D
【详解】
由勾股定理可知,
∵OB=22+12=5,∴这个点表示的实数是5.
故选D.
?
课堂练习
2.如图,AB=AC,则数轴上点C所表示的数为( )
A.5 +1 B.5﹣1 C.﹣5 +1 D.﹣5﹣1
?
【答案】B
【详解】
解:由勾股定理得:AB=22+12=5,
∴AC=AB=5,
∴数轴上点C所表示的数为5?1.
故选B.
?
3.如图,网格中每个小正方形的边长均为1,点????,????,????都在格点上,以????为圆心,????????为半径画弧,交最上方的网格线于点????,则????????的长为( )
A.5 B.0. 8
C.3?5 D.13
?
【答案】C
【详解】
如图,连接AD,则AD=AB=3,
由勾股定理可得,Rt△ADE中,DE= ????????2?????????2=5,
又∵CE=3,∴CD=3-5,
故选:C.
?
如图,OP=1,过点P作PP1⊥OP,且PP1=1,得OP1=2;再过点P1作P1P2⊥OP1且P1P2=1,得OP2=3;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2……依此法继续作下去,得OP2018的值为( )
A.2016 B.2017
C.2018 D.2019
?
【答案】D
【详解】∵OP=1,OP1=2,OP2=3,OP3=4=2,
∴OP4=5,…,
OP2018=2019.
故选:D
?
写出如图格点△ABC各顶点的坐标,求出此三角形的周长.
【答案】A(2,2)、B(-2,-1)、C(3,-2),面积9.5平方单位
【详解】
由图可知,A(2,2),B(-2,-1),C(3,-2).
AB=32+42=5,
AC=12+42=17,
BC=12+52=26,
故周长=5+17+26.
?
1.如图,在四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=42,CD=22,点P在四边形ABCD的边上,若点P到BD的距离为3,则点P的个数为( )
A.2 B.3 C.4 D.5
?
分析:首先作出AB、AD边上的点P(点A)到BD的垂线段AE,即点P到BD的最长距离,作出BC、CD的点P(点C)到BD的垂线段CF,即点P到BD的最长距离,由已知计算出AE、CF的长与3比较得出答案。
A
拓展提升
解析:过点A作AE⊥BD于E,过点C作CF⊥BD于F,
∵∠BAD=∠ADC=90°,AB=AD=4 2,CD=2 2,
∴∠ABD=∠ADB=45°,
∴∠CDF=90°-∠ADB=45°,
∵sin∠ABD=AEAB,
∴AE=AB?sin∠ABD=4 2?sin45°=4>3,
CF=22CD═2<3,所以在AB和AD边上有符合P到BD的距离为3的点2个,故选A。
?
1、表示无理数
利用勾股定理的知识在数轴上表示无理数。
课堂小结
谢谢聆听
第三课时 利用勾股定理表示无理数的点
第十七章 勾股定理
2021年春人教版八年级(下)数学
1.利用勾股定理画出一条线段等于已知长度为无理数的线段。
2.通过学习勾股定理的应用,培养学生基本运算能力和应用意识。
利用勾股定理画出一条线段等于已知长度为无理数的线段。(重点)
利用勾股定理解决几何问题。(难点)??
学习目标
探索与思考
八年级上册中我们曾经通过画图得到结论:斜边和一条直角边对应相等的两个直角三角形全等. 学习了勾股定理后,你能证明这一结论吗?
A
B
C
A ′
B ′
C′
已知:如图,在Rt △ABC和Rt △A ′ B ′ C ′中,
∠C= ∠C ′,AB=A ′B ′,AC=A ′C ′.
求证: △ABC ≌ △A ′ B ′ C ′.
证明:在Rt △ABC和Rt △A ′ B ′ C ′中,∠C= 90°,
根据勾股定理,得BC = ????????????????????????? , B’C’ = ????′????′?????????′????′????
又 AB = A ′B ′,AC = A ′C ′,
∴BC = B ′ C ′.
∴ △ABC ≌ △A ′ B ′ C ′(SSS).
?
在Rt△ABC中,若AC= 13,求AB边和BC边的边长?
?
A
B
C
{69CF1AB2-1976-4502-BF36-3FF5EA218861}
AB
BC
1
23
?
1
23
?
2
3
2
3
?
3
?
10
?
2
?
11
?
…
?
…
?
结合上面表格内容,尝试在数轴上画出????????的点?
你会选择哪一组数据呢?
?
探索与思考
数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示????????的点吗?
?
0
1
2
3
4
????????
?
你能在数轴上画出表示????????的点吗?
?
探索与思考
数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示????的点吗?
?
0
1
2
3
4
????
?
你能在数轴上画出表示????的点吗?
?
????
?
探索与思考
利用勾股定理作出长为????, ????, ????, ????…的线段.
?
探索与思考
O
3
1.如图,矩形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是( )
A.25 B.22 C.3 D.5
?
【答案】D
【详解】
由勾股定理可知,
∵OB=22+12=5,∴这个点表示的实数是5.
故选D.
?
课堂练习
2.如图,AB=AC,则数轴上点C所表示的数为( )
A.5 +1 B.5﹣1 C.﹣5 +1 D.﹣5﹣1
?
【答案】B
【详解】
解:由勾股定理得:AB=22+12=5,
∴AC=AB=5,
∴数轴上点C所表示的数为5?1.
故选B.
?
3.如图,网格中每个小正方形的边长均为1,点????,????,????都在格点上,以????为圆心,????????为半径画弧,交最上方的网格线于点????,则????????的长为( )
A.5 B.0. 8
C.3?5 D.13
?
【答案】C
【详解】
如图,连接AD,则AD=AB=3,
由勾股定理可得,Rt△ADE中,DE= ????????2?????????2=5,
又∵CE=3,∴CD=3-5,
故选:C.
?
如图,OP=1,过点P作PP1⊥OP,且PP1=1,得OP1=2;再过点P1作P1P2⊥OP1且P1P2=1,得OP2=3;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2……依此法继续作下去,得OP2018的值为( )
A.2016 B.2017
C.2018 D.2019
?
【答案】D
【详解】∵OP=1,OP1=2,OP2=3,OP3=4=2,
∴OP4=5,…,
OP2018=2019.
故选:D
?
写出如图格点△ABC各顶点的坐标,求出此三角形的周长.
【答案】A(2,2)、B(-2,-1)、C(3,-2),面积9.5平方单位
【详解】
由图可知,A(2,2),B(-2,-1),C(3,-2).
AB=32+42=5,
AC=12+42=17,
BC=12+52=26,
故周长=5+17+26.
?
1.如图,在四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=42,CD=22,点P在四边形ABCD的边上,若点P到BD的距离为3,则点P的个数为( )
A.2 B.3 C.4 D.5
?
分析:首先作出AB、AD边上的点P(点A)到BD的垂线段AE,即点P到BD的最长距离,作出BC、CD的点P(点C)到BD的垂线段CF,即点P到BD的最长距离,由已知计算出AE、CF的长与3比较得出答案。
A
拓展提升
解析:过点A作AE⊥BD于E,过点C作CF⊥BD于F,
∵∠BAD=∠ADC=90°,AB=AD=4 2,CD=2 2,
∴∠ABD=∠ADB=45°,
∴∠CDF=90°-∠ADB=45°,
∵sin∠ABD=AEAB,
∴AE=AB?sin∠ABD=4 2?sin45°=4>3,
CF=22CD═2<3,所以在AB和AD边上有符合P到BD的距离为3的点2个,故选A。
?
1、表示无理数
利用勾股定理的知识在数轴上表示无理数。
课堂小结
谢谢聆听
