正弦函数、余弦函数的图象
图片预览



文档简介
(共15张PPT)
§1.4.1正弦函数、余弦函数的图象
复习
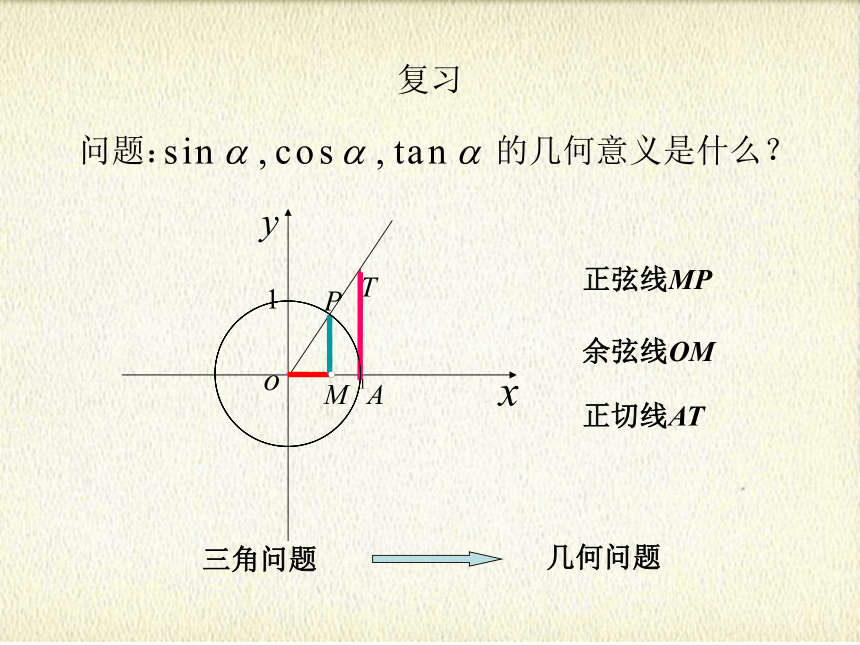
问题: 的几何意义是什么?
o
1
1
P
M
A
T
正弦线MP
余弦线OM
正切线AT
三角问题
几何问题
正弦函数图象画法探究
1.能否用描点法作函数y=sinx, x∈[0,2π]的图象
只要能够确定该图象上的点(x,sinx) 的坐标,就可以用描点法作出函数图象。而该图象上点的坐标可通过x的值查三角函数表得到。
2.能否不通过查表得到点(x,sinx)的坐标
可以利用与单位圆有关的三角函数线
正弦、余弦函数的图象
问题:如何作出正弦的图象?
途径:利用单位圆中正弦线(表示正弦)来解决.
步骤:列表,描点,连线.
y=sinx x [0,2 ]
O1
O
y
x
-1
1
y=sinx x R
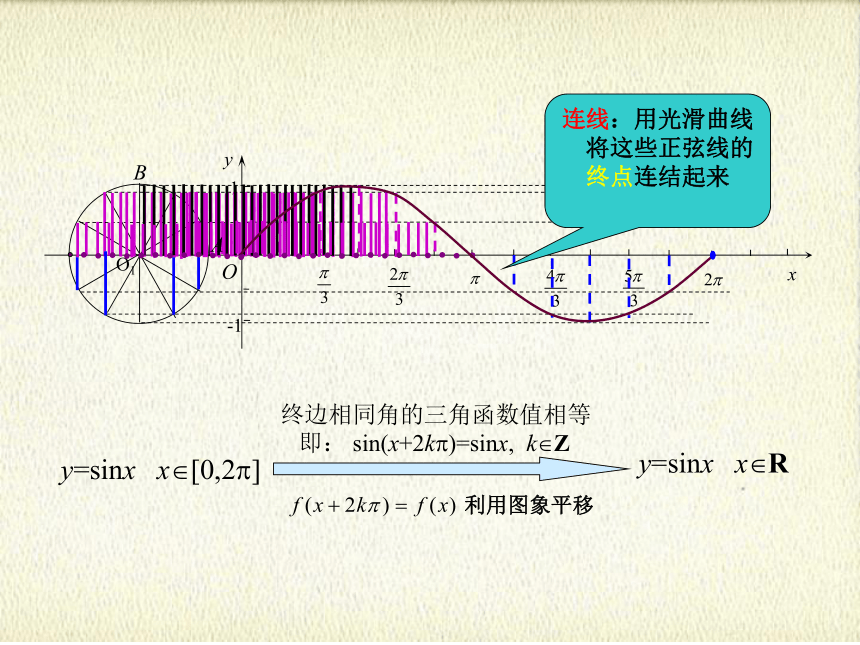
终边相同角的三角函数值相等
即: sin(x+2k )=sinx, k Z
连线:用光滑曲线
将这些正弦线的终点连结起来
利用图象平移
A
B
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
y
x
o
1
-1
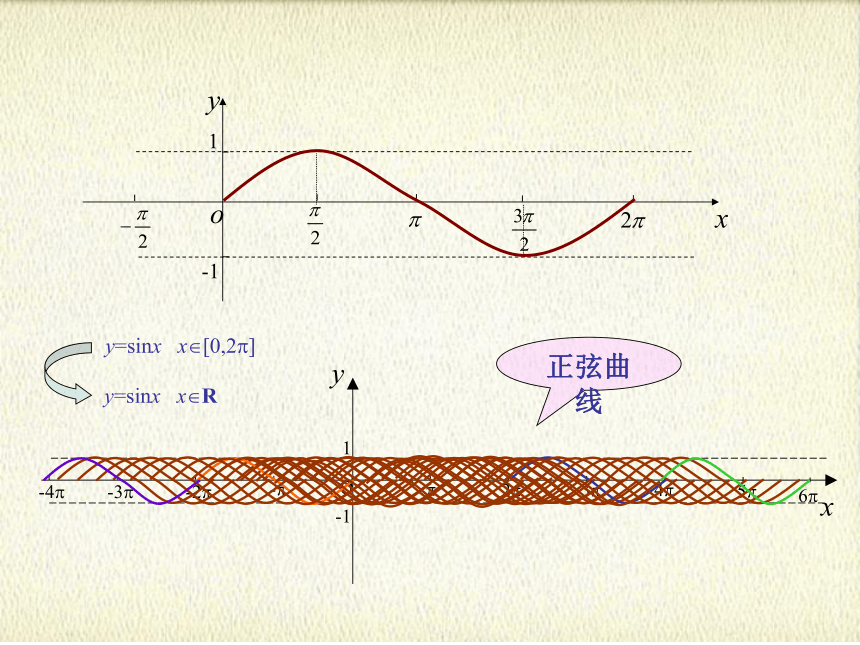
y=sinx x [0,2 ]
y=sinx x R
正弦曲线
y
x
o
1
-1
如何作出正弦函数的图象(在精确度要求不太高时)?
(0,0)
( ,1)
( ,0)
( ,-1)
( 2 ,0)
五点画图法
五点法—
(0,0)
( ,1)
( ,0)
( ,1)
( 2 ,0)
(0,0)
( ,1)
( ,0)
( ,1)
( 2 ,0)
(0,0)
( ,1)
( ,0)
( ,1)
( 2 ,0)
(0,0)
( ,1)
( ,0)
( ,1)
( 2 ,0)
(0,0)
( ,1)
( ,0)
( ,-1)
( 2 ,0)
(0,0)
( ,1)
( ,0)
( ,-1)
( 2 ,0)
(0,0)
( ,1)
( ,0)
( ,-1)
( 2 ,0)
(0,0)
( ,1)
( ,0)
( ,-1)
( 2 ,0)
x
sin x
0 2
0
1
0
-1
0
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
余弦函数的图象
正弦函数的图象
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
y=cosx=sin(x+ ), x R
余弦曲线
(0,1)
( ,0)
( ,-1)
( ,0)
( 2 ,1)
正弦曲线
形状完全一样只是位置不同
例1 画出函数y=1+sinx,x [0, 2 ]的简图:
x
sin x
1+sin x
0 2
0
1
0
-1
0
1 2 1 0 1
o
1
y
x
-1
2
y=sinx,x [0, 2 ]
y=1+sinx,x [0, 2 ]
步骤:
1.列表
2.描点
3.连线
例2 画出函数y= - cosx,x [0, 2 ]的简图:
x
cos x
- cos x
0 2
1
0
-1
0
1
-1 0 1 0 -1
y
x
o
1
-1
y= - cosx,x [0, 2 ]
y=cosx,x [0, 2 ]
练习:在同一直角坐标系内画
出 和 的图象.
再谈图象变换
画出下列函数的草图
还记得吗:
1、平移变换
2、翻折变换
3、对称变换
4、伸缩变换
这是唯一的途径吗?你还想到什么方法?
小 结
1. 正弦曲线、余弦曲线的联系和区别;
2.五点作图法:与x轴的交点,最高点,最低点,即x取
y
x
o
1
-1
y=sinx,x [0, 2 ]
y=cosx,x [0, 2 ]
§1.4.1正弦函数、余弦函数的图象
复习
问题: 的几何意义是什么?
o
1
1
P
M
A
T
正弦线MP
余弦线OM
正切线AT
三角问题
几何问题
正弦函数图象画法探究
1.能否用描点法作函数y=sinx, x∈[0,2π]的图象
只要能够确定该图象上的点(x,sinx) 的坐标,就可以用描点法作出函数图象。而该图象上点的坐标可通过x的值查三角函数表得到。
2.能否不通过查表得到点(x,sinx)的坐标
可以利用与单位圆有关的三角函数线
正弦、余弦函数的图象
问题:如何作出正弦的图象?
途径:利用单位圆中正弦线(表示正弦)来解决.
步骤:列表,描点,连线.
y=sinx x [0,2 ]
O1
O
y
x
-1
1
y=sinx x R
终边相同角的三角函数值相等
即: sin(x+2k )=sinx, k Z
连线:用光滑曲线
将这些正弦线的终点连结起来
利用图象平移
A
B
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
y
x
o
1
-1
y=sinx x [0,2 ]
y=sinx x R
正弦曲线
y
x
o
1
-1
如何作出正弦函数的图象(在精确度要求不太高时)?
(0,0)
( ,1)
( ,0)
( ,-1)
( 2 ,0)
五点画图法
五点法—
(0,0)
( ,1)
( ,0)
( ,1)
( 2 ,0)
(0,0)
( ,1)
( ,0)
( ,1)
( 2 ,0)
(0,0)
( ,1)
( ,0)
( ,1)
( 2 ,0)
(0,0)
( ,1)
( ,0)
( ,1)
( 2 ,0)
(0,0)
( ,1)
( ,0)
( ,-1)
( 2 ,0)
(0,0)
( ,1)
( ,0)
( ,-1)
( 2 ,0)
(0,0)
( ,1)
( ,0)
( ,-1)
( 2 ,0)
(0,0)
( ,1)
( ,0)
( ,-1)
( 2 ,0)
x
sin x
0 2
0
1
0
-1
0
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
余弦函数的图象
正弦函数的图象
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
y=cosx=sin(x+ ), x R
余弦曲线
(0,1)
( ,0)
( ,-1)
( ,0)
( 2 ,1)
正弦曲线
形状完全一样只是位置不同
例1 画出函数y=1+sinx,x [0, 2 ]的简图:
x
sin x
1+sin x
0 2
0
1
0
-1
0
1 2 1 0 1
o
1
y
x
-1
2
y=sinx,x [0, 2 ]
y=1+sinx,x [0, 2 ]
步骤:
1.列表
2.描点
3.连线
例2 画出函数y= - cosx,x [0, 2 ]的简图:
x
cos x
- cos x
0 2
1
0
-1
0
1
-1 0 1 0 -1
y
x
o
1
-1
y= - cosx,x [0, 2 ]
y=cosx,x [0, 2 ]
练习:在同一直角坐标系内画
出 和 的图象.
再谈图象变换
画出下列函数的草图
还记得吗:
1、平移变换
2、翻折变换
3、对称变换
4、伸缩变换
这是唯一的途径吗?你还想到什么方法?
小 结
1. 正弦曲线、余弦曲线的联系和区别;
2.五点作图法:与x轴的交点,最高点,最低点,即x取
y
x
o
1
-1
y=sinx,x [0, 2 ]
y=cosx,x [0, 2 ]
