两点间的距离
图片预览




文档简介
(共20张PPT)
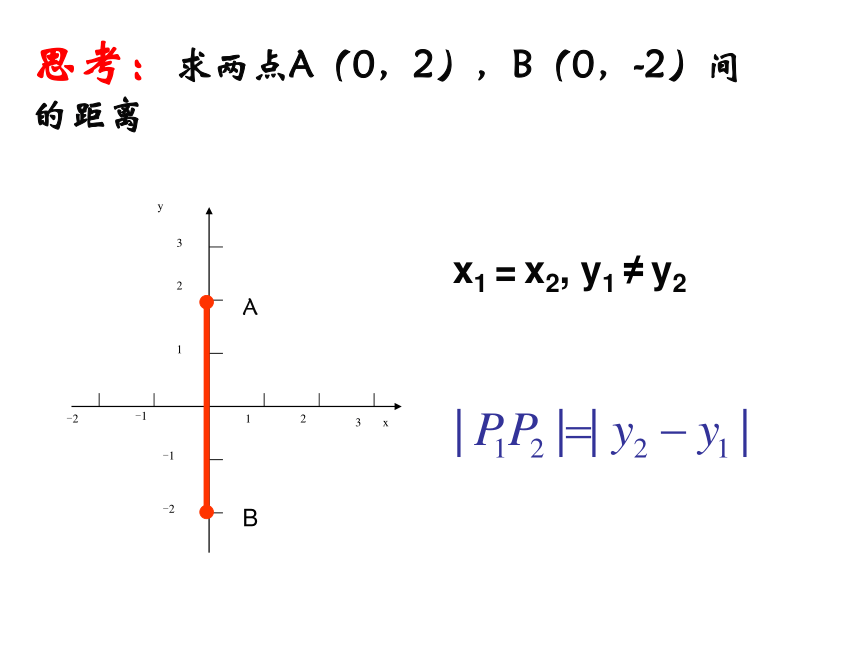
思考:求两点A(0,2),B(0,-2)间的距离
1
1
2
2
3
3
-1
-1
-2
-2
y
x
A
B
x1 = x2, y1 ≠ y2
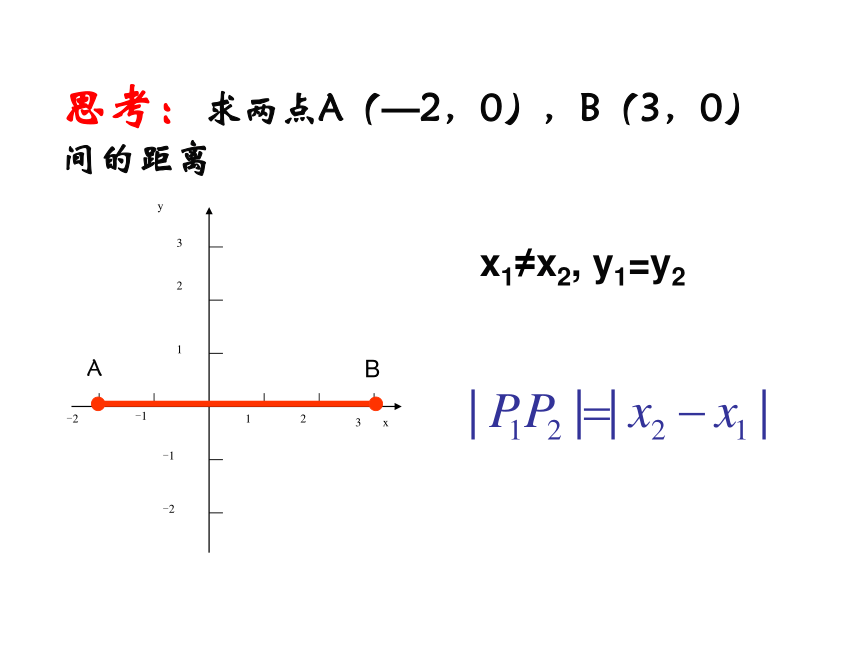
思考:求两点A(—2,0),B(3,0)间的距离
1
1
2
2
3
3
-1
-1
-2
-2
y
x
A
B
x1≠x2, y1=y2
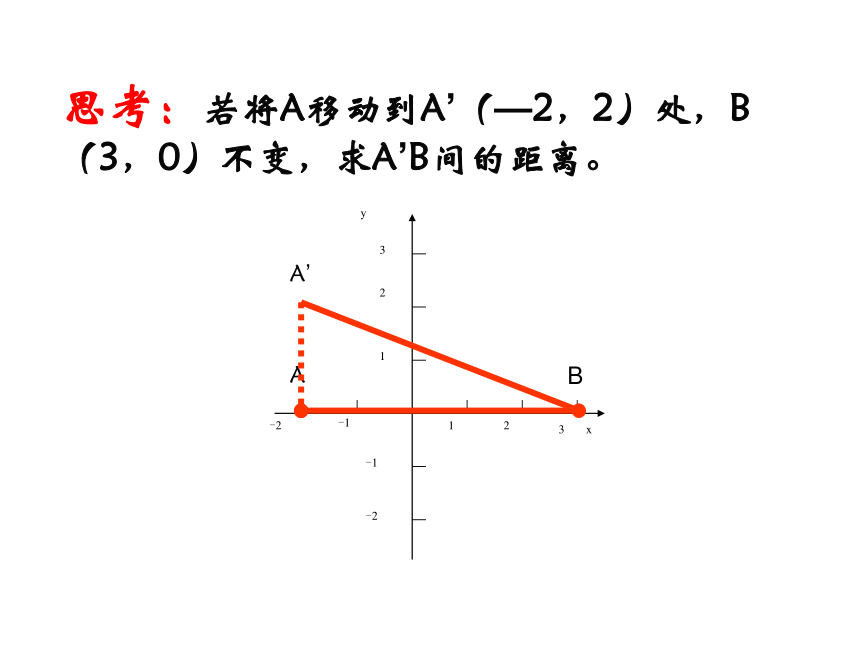
思考:若将A移动到A’(—2,2)处,B(3,0)不变,求A’B间的距离。
1
1
2
2
3
3
-1
-1
-2
-2
y
x
A
B
A’
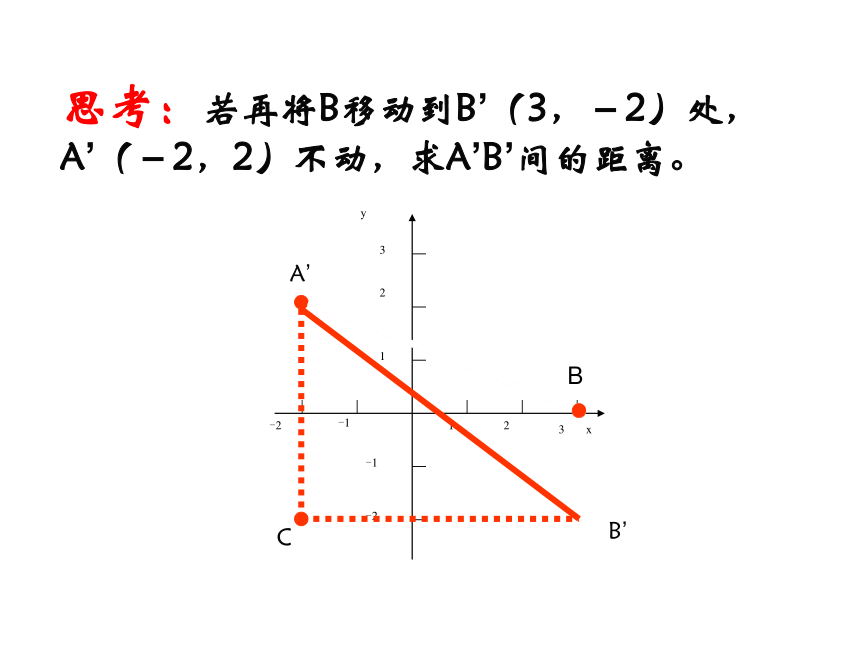
思考:若再将B移动到B’(3,-2)处, A’(-2,2)不动,求A’B’间的距离。
1
1
2
2
3
3
-1
-1
-2
-2
y
x
B’
B
A’
C
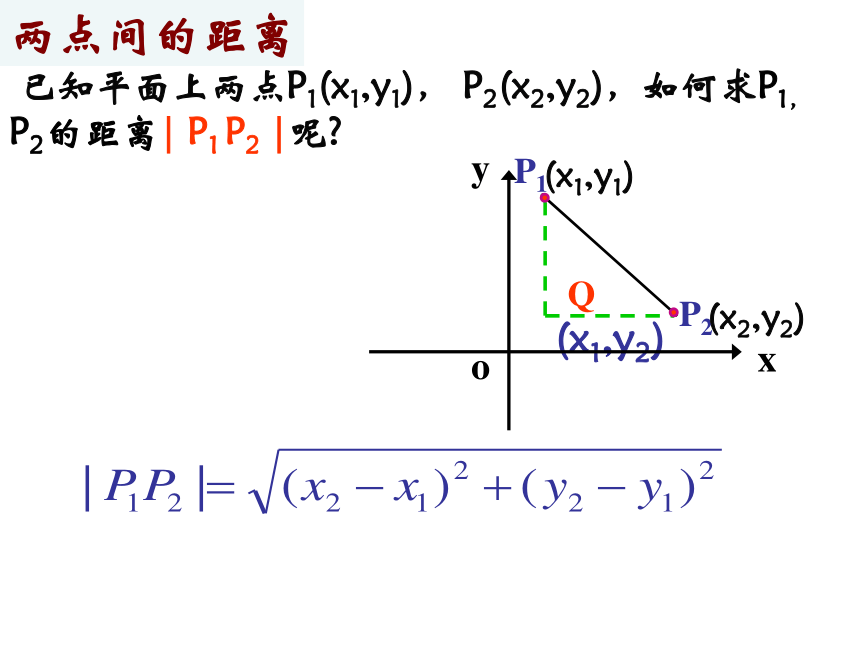
已知平面上两点P1(x1,y1), P2(x2,y2),如何求P1, P2的距离| P1 P2 |呢
两点间的距离
Q
(x1,y2)
y
x
o
P1
P2
(x1,y1)
(x2,y2)
已知平面上两点P1(x1,y1), P2(x2,y2),如何求P1, P2的距离| P1 P2 |呢
两点间的距离公式
(1) x1≠x2, y1=y2
(2) x1 = x2, y1 ≠ y2
特别的:
2
2
|
|
:
)
,
(
y
x
OP
y
x
P
O
+
=
的距离
与任一点
原点
(3)
练习
1、求下列两点间的距离:
(1)、A(6,0),B(-2,0) (2)、C(0,-4),D(0,-1)
(3)、P(6,0),Q(0,-2) (4)、M(2,1),N(5,-1)
解:
(1)
(2)
(3)
(4)
例题分析
解:设所求点为P(x,0),于是有
解得x=1,所以所求点P(1,0)
2、求在x轴上与点A(5,12)的距离为13的点的坐标;
练习
3、已知点P的横坐标是7,点P与点N(-1,5)间的距离等于10,求点P的纵坐标。
例题分析
例:证明平行四边形四条边的平方和等于两条对角线的平方和。
y
x
o
(b,c)
(a+b,c)
(a,0)
(0,0)
A
B
D
C
y
x
o
(b ,c)
(a+b ,c)
(a,0)
(0,0)
解:如图,以顶点A为坐标原点,AB所在直线为x轴,建立直角坐标系,则有A(0,0)。
设B(a,0),D(b,c),由平行四边形的性质可得C(a+b,c)
A
B
D
C
点C的纵坐标等于
点D的纵坐标
C、D两点横
坐标之差为a
例:证明平行四边形四条边的平方和等于两条对角线的平方和。
因此,平行四边形四条边的平方和等于两条对角线的平方和。
y
x
o
(b,c)
(a+b,c)
(a,0)
(0,0)
A
B
D
C
第一步:建立坐标系,用坐标表示有关的量;
第二步:进行有关的代数运算;
第三步:把代数运算结果“翻译”所几何关系.
在例4中,是否还有其他的建立坐标系的方法?
思考
实际上,本题还可以以对角线的交点为原点,一条对角线所在直线为x轴建立直角坐标系来证明。
y
x
o
A
B
D
C
(a,c)
(-a,-c)
(b,d)
(-b,d)
设点C的坐标为(a,c),点B的坐标为(b,d)(a,b,c,d都是正数),由平行四边形的性质可知,点A的坐标为(-a,-c),点D的坐标为(-b,-d)。
y
x
o
A
B
D
C
解决例4的问题,上面两种建系方法都比较简单,但若是以A点位坐标原点,AB所在直线为x轴建立直角坐标系的话,显然C,D点的坐标将会变得比较复杂。
要认真体会适当建立坐标系对证明的重要性,它可以简化计算。
y
x
o
(b,c)
(a+b,c)
(a,0)
(0,0)
A
B
D
C
(a,c)
(-a,-c)
(b,d)
(-b,-d)
y
x
o
A
B
D
C
练习
5、证明直角三角形斜边的中点到三个顶点的距离相等。
y
x
o
B
C
A
M
(0,0)
(a,0)
(0,b)
练习:已知△ABC的三个顶点A
(-1,0),B(1,0),C( )
试判断△ABC的形状.
分析:计算三边的长,比较后可得结论.
思考
1、平面内两点P1(x1,y1), P2(x2,y2) 的距离公式是
小结
2、坐标法证明简单平面几何问题的步骤
第一步:建立坐标系,用坐标表示有关的量;
第二步:进行有关的代数运算;
第三步:把代数运算结果“翻译”所几何关系.
思考:求两点A(0,2),B(0,-2)间的距离
1
1
2
2
3
3
-1
-1
-2
-2
y
x
A
B
x1 = x2, y1 ≠ y2
思考:求两点A(—2,0),B(3,0)间的距离
1
1
2
2
3
3
-1
-1
-2
-2
y
x
A
B
x1≠x2, y1=y2
思考:若将A移动到A’(—2,2)处,B(3,0)不变,求A’B间的距离。
1
1
2
2
3
3
-1
-1
-2
-2
y
x
A
B
A’
思考:若再将B移动到B’(3,-2)处, A’(-2,2)不动,求A’B’间的距离。
1
1
2
2
3
3
-1
-1
-2
-2
y
x
B’
B
A’
C
已知平面上两点P1(x1,y1), P2(x2,y2),如何求P1, P2的距离| P1 P2 |呢
两点间的距离
Q
(x1,y2)
y
x
o
P1
P2
(x1,y1)
(x2,y2)
已知平面上两点P1(x1,y1), P2(x2,y2),如何求P1, P2的距离| P1 P2 |呢
两点间的距离公式
(1) x1≠x2, y1=y2
(2) x1 = x2, y1 ≠ y2
特别的:
2
2
|
|
:
)
,
(
y
x
OP
y
x
P
O
+
=
的距离
与任一点
原点
(3)
练习
1、求下列两点间的距离:
(1)、A(6,0),B(-2,0) (2)、C(0,-4),D(0,-1)
(3)、P(6,0),Q(0,-2) (4)、M(2,1),N(5,-1)
解:
(1)
(2)
(3)
(4)
例题分析
解:设所求点为P(x,0),于是有
解得x=1,所以所求点P(1,0)
2、求在x轴上与点A(5,12)的距离为13的点的坐标;
练习
3、已知点P的横坐标是7,点P与点N(-1,5)间的距离等于10,求点P的纵坐标。
例题分析
例:证明平行四边形四条边的平方和等于两条对角线的平方和。
y
x
o
(b,c)
(a+b,c)
(a,0)
(0,0)
A
B
D
C
y
x
o
(b ,c)
(a+b ,c)
(a,0)
(0,0)
解:如图,以顶点A为坐标原点,AB所在直线为x轴,建立直角坐标系,则有A(0,0)。
设B(a,0),D(b,c),由平行四边形的性质可得C(a+b,c)
A
B
D
C
点C的纵坐标等于
点D的纵坐标
C、D两点横
坐标之差为a
例:证明平行四边形四条边的平方和等于两条对角线的平方和。
因此,平行四边形四条边的平方和等于两条对角线的平方和。
y
x
o
(b,c)
(a+b,c)
(a,0)
(0,0)
A
B
D
C
第一步:建立坐标系,用坐标表示有关的量;
第二步:进行有关的代数运算;
第三步:把代数运算结果“翻译”所几何关系.
在例4中,是否还有其他的建立坐标系的方法?
思考
实际上,本题还可以以对角线的交点为原点,一条对角线所在直线为x轴建立直角坐标系来证明。
y
x
o
A
B
D
C
(a,c)
(-a,-c)
(b,d)
(-b,d)
设点C的坐标为(a,c),点B的坐标为(b,d)(a,b,c,d都是正数),由平行四边形的性质可知,点A的坐标为(-a,-c),点D的坐标为(-b,-d)。
y
x
o
A
B
D
C
解决例4的问题,上面两种建系方法都比较简单,但若是以A点位坐标原点,AB所在直线为x轴建立直角坐标系的话,显然C,D点的坐标将会变得比较复杂。
要认真体会适当建立坐标系对证明的重要性,它可以简化计算。
y
x
o
(b,c)
(a+b,c)
(a,0)
(0,0)
A
B
D
C
(a,c)
(-a,-c)
(b,d)
(-b,-d)
y
x
o
A
B
D
C
练习
5、证明直角三角形斜边的中点到三个顶点的距离相等。
y
x
o
B
C
A
M
(0,0)
(a,0)
(0,b)
练习:已知△ABC的三个顶点A
(-1,0),B(1,0),C( )
试判断△ABC的形状.
分析:计算三边的长,比较后可得结论.
思考
1、平面内两点P1(x1,y1), P2(x2,y2) 的距离公式是
小结
2、坐标法证明简单平面几何问题的步骤
第一步:建立坐标系,用坐标表示有关的量;
第二步:进行有关的代数运算;
第三步:把代数运算结果“翻译”所几何关系.
