1.3y=Asin(ωx+φ)的图象变换课件(苏教版必修4)
文档属性
| 名称 | 1.3y=Asin(ωx+φ)的图象变换课件(苏教版必修4) |

|
|
| 格式 | rar | ||
| 文件大小 | 362.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-22 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
函数 y=Asin( x+ ) 的图象
复习练习
1. 要得到函数 y= 2 sin x 的图象,只需将 y= sinx 图象( )
A.横坐标扩大原来的两倍 B. 纵坐标扩大原来的两倍
C.横坐标扩大到原来的两倍 D. 纵坐标扩大到原来的两倍
2. 要得到函数 y=sin3x 的图象,只需将 y=sinx 图象( )
A. 横坐标扩大原来的3倍 B.横坐标扩大到原来的3倍
C. 横坐标缩小原来的1/3倍 D.横坐标缩小到原来的1/3倍
3. 要得到函数 y=sin(x + π/3)的图象,只需将 y=sinx 图象( )
A. 向左平移π/6个单位 B. 向右平移π/6个单位
C. 向左平移π/3个单位 D. 向右平移π/3个单位
4. 要得到函数 y=sin(2x-π/3)的图象,只需将y=sin2x图象( )
A. 向左平移π/3 个单位 B. 向右平移π/3个单位
C. 向左平移π/ 6个单位 D. 向右平移π/6 个单位
( 弹簧振子演示)
D
D
C
D
例1 作函数 y = 3sin(2 + )的简图
分析 :
因为T= ,所以用“五点法”先作长度为一个周期的闭区
间上的简图
设:
那么:
且
当 X 取 0,
, , , 时,可求得相对应的 、y 的
值,得到“五点”,再描点作图 。然后将简图左右扩展。
y=3sin(2x+ )
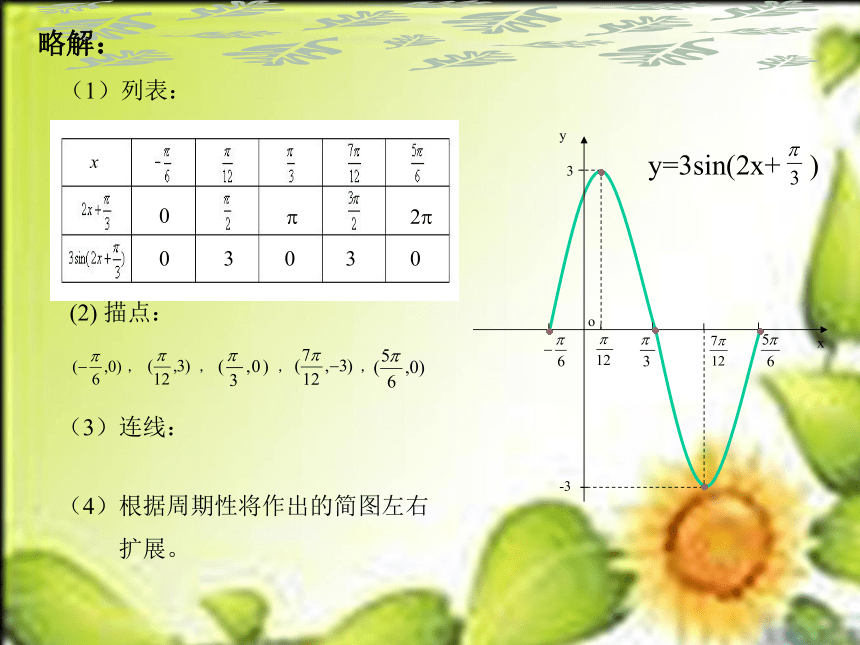
略解:
(2) 描点:
, , , ,
(3)连线:
(4)根据周期性将作出的简图左右
扩展。
0
0
0
0
3
3
2
(1)列表:
x
y
o
3
-3
函数 y=sinx y=sin(x+ ) 的图象
(3)横坐标不变
纵坐标伸长到原来的3倍
y=3sin(2x+ )的图象
y=sin(2x+ ) 的图象
(1)向左平移
纵坐标不变
(2)横坐标缩短到原来的 倍
1
-1
2
-2
o
x
y
3
-3
2
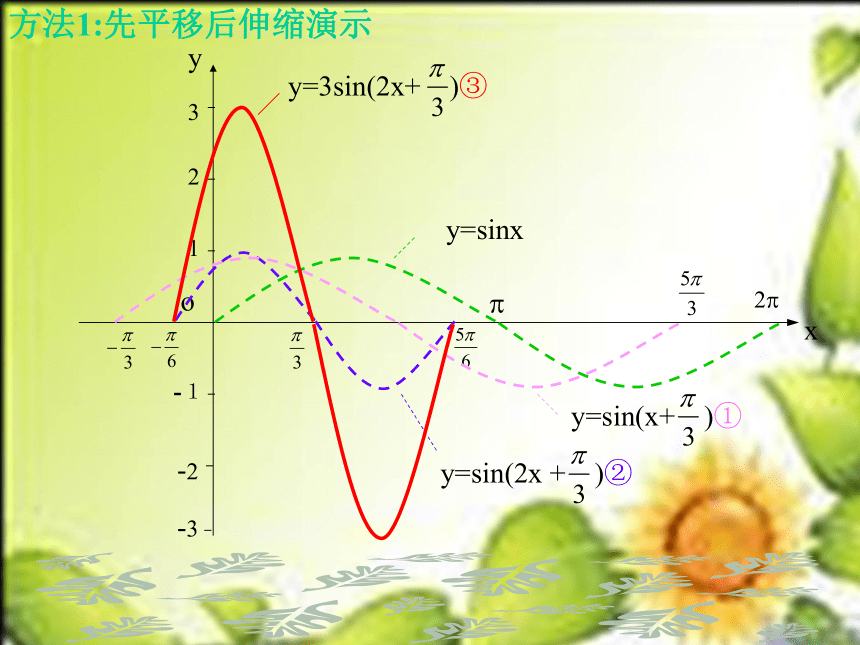
y=sin(2x + )②
y=sinx
y=sin(x+ )①
y=3sin(2x+ )③
方法1:先平移后伸缩演示
y=Sin( x+ ) 的图象
函数 y=Sinx y=Sin(x+ ) 的图象
(3)纵坐标伸长(A>1)或缩短(0到原来的A倍(横坐标不变)
y=ASin( x+ )的图象
(1)向左( >0)或向右( <0)
平移| |个单位
(2)横坐标缩短( >1)或伸长(0< <1)到
原来的 倍,(纵坐标不变)
方法1:先平移后伸缩一般规律
(3)横坐标不变
纵坐标伸长到原来的3倍
y=3Sin(2x+ )的图象
y=Sin(2x+ ) 的图象
(1)横坐标缩短到原来的 倍
纵坐标不变
(2) 向左平移
函数 y=Sinx y=Sin2x的图象
1
-1
2
-2
o
x
y
3
-3
2
y=sin(2x + )②
y=sinx
y=3sin(2x+ )③
y=sin2x①
方法2:先伸缩后平移演示
y=Sin( x+ ) 的图象
(3)横坐标不变,纵坐标伸长(A>1)
或缩短(0y=ASin( x+ )的图象
函数 y=Sinx y=Sin x 的图象
(1)横坐标缩短( >1)或伸长(0< <1)到
原来的 倍,纵坐标不变
(2)向左( >0)或向右( <0)
平移| |个单位
方法2:先伸缩后平移一般规律
1
-1
2
-2
o
x
y
3
-3
2
y=sinx
y=3sin(2x+ )③
y=3sinx①
y=3sin2x②
其余方法演示 ….
例2、如图所示 ,弹簧挂着的物体作上下振动,它在时间 t(秒)内离开平衡位置(就是静止时的位置)的位移 S (cm) 由 函 S = 5sin(π/2 t + π/4 ) 决定,
(1) 试求物体离开平衡位置的最大距离;
(2 试求物体往复振动一次所需的时间;
(3) 试求物体每秒钟内往复振动的次数;
解:演示课件(点击此处)
练习: (点击空白处)
练习
1、 当函数 y = -5sin (-2x +π/4) 表示一个振动量时其振幅为 周期为 ______
频率为 相位为 初相为 ;
2、将函数 y= sin2x 的图象向左平移 π/ 6 得到的曲线对应的解析式为( )
A. y=sin(2x+π/6) B. y=sin(2x-π/6)
C. y=sin(2x+π/3) D. y=sin(2x-π/3)
3、要得到函数 y = cos3x 的图象,只需将函数 y = cos (3x-π/ 6) 的图象( )
A. 向左平移π/6个单位 B. 向右平移π/6个单位
C. 向左平移π/18个单位 D. 向右平移π/18个单位
4、函数 y = 3sin( x/ 2 + π/3) 的图象可由函数 y = 3 sin x 经( )变换而得;
A. 先把横坐标扩大到原来的两倍(纵坐标不变) ,再向左平移π/6个单位
B. 先把横坐标缩短到原来的1/2倍(纵坐标不变) ,再向右平移π/3个单位
C. 先向右平移π/3个单位 ,再把横坐标缩短到原来的1/2倍(纵坐标不变)
D. 先向左平移π/3个单位 ,再把横坐标扩大到原来的两倍(纵坐标不变)
*5、要得到函数 y = cos ( 2x -π/4) 的图象,只需将函数 y = sin 2 x 的图象( )
A. 向左平移π/4个单位 B. 向右平移π / 4 个单位
C. 向左平移π/ 8个单位 D. 向右平移π/ 8个单位
5
π
1/ π
-2x +π/4
π/ 4
C
C
D
D
小结:
1、作正弦型函数y=Asin( x+ ) 的图象的方法:
(1)用“五点法”作图;
(2)利用变换关系作图。
2、函数 y = sinx 的图象与函数 y=Asin( x+ )的图象间的变换关系。
3、余弦型函数 y=Acos( x+ ) 的相关问题同样处理。
y = sinx 的图象 y=Asin( x+ )
Y = sin( x+ )
y=sin(x+ )
y=sin x
4 、 函数的物理背景
《函数y=Asin(ωx+φ)的图象》
函数 y=Asin( x+ ) 的图象
复习练习
1. 要得到函数 y= 2 sin x 的图象,只需将 y= sinx 图象( )
A.横坐标扩大原来的两倍 B. 纵坐标扩大原来的两倍
C.横坐标扩大到原来的两倍 D. 纵坐标扩大到原来的两倍
2. 要得到函数 y=sin3x 的图象,只需将 y=sinx 图象( )
A. 横坐标扩大原来的3倍 B.横坐标扩大到原来的3倍
C. 横坐标缩小原来的1/3倍 D.横坐标缩小到原来的1/3倍
3. 要得到函数 y=sin(x + π/3)的图象,只需将 y=sinx 图象( )
A. 向左平移π/6个单位 B. 向右平移π/6个单位
C. 向左平移π/3个单位 D. 向右平移π/3个单位
4. 要得到函数 y=sin(2x-π/3)的图象,只需将y=sin2x图象( )
A. 向左平移π/3 个单位 B. 向右平移π/3个单位
C. 向左平移π/ 6个单位 D. 向右平移π/6 个单位
( 弹簧振子演示)
D
D
C
D
例1 作函数 y = 3sin(2 + )的简图
分析 :
因为T= ,所以用“五点法”先作长度为一个周期的闭区
间上的简图
设:
那么:
且
当 X 取 0,
, , , 时,可求得相对应的 、y 的
值,得到“五点”,再描点作图 。然后将简图左右扩展。
y=3sin(2x+ )
略解:
(2) 描点:
, , , ,
(3)连线:
(4)根据周期性将作出的简图左右
扩展。
0
0
0
0
3
3
2
(1)列表:
x
y
o
3
-3
函数 y=sinx y=sin(x+ ) 的图象
(3)横坐标不变
纵坐标伸长到原来的3倍
y=3sin(2x+ )的图象
y=sin(2x+ ) 的图象
(1)向左平移
纵坐标不变
(2)横坐标缩短到原来的 倍
1
-1
2
-2
o
x
y
3
-3
2
y=sin(2x + )②
y=sinx
y=sin(x+ )①
y=3sin(2x+ )③
方法1:先平移后伸缩演示
y=Sin( x+ ) 的图象
函数 y=Sinx y=Sin(x+ ) 的图象
(3)纵坐标伸长(A>1)或缩短(0
y=ASin( x+ )的图象
(1)向左( >0)或向右( <0)
平移| |个单位
(2)横坐标缩短( >1)或伸长(0< <1)到
原来的 倍,(纵坐标不变)
方法1:先平移后伸缩一般规律
(3)横坐标不变
纵坐标伸长到原来的3倍
y=3Sin(2x+ )的图象
y=Sin(2x+ ) 的图象
(1)横坐标缩短到原来的 倍
纵坐标不变
(2) 向左平移
函数 y=Sinx y=Sin2x的图象
1
-1
2
-2
o
x
y
3
-3
2
y=sin(2x + )②
y=sinx
y=3sin(2x+ )③
y=sin2x①
方法2:先伸缩后平移演示
y=Sin( x+ ) 的图象
(3)横坐标不变,纵坐标伸长(A>1)
或缩短(0
函数 y=Sinx y=Sin x 的图象
(1)横坐标缩短( >1)或伸长(0< <1)到
原来的 倍,纵坐标不变
(2)向左( >0)或向右( <0)
平移| |个单位
方法2:先伸缩后平移一般规律
1
-1
2
-2
o
x
y
3
-3
2
y=sinx
y=3sin(2x+ )③
y=3sinx①
y=3sin2x②
其余方法演示 ….
例2、如图所示 ,弹簧挂着的物体作上下振动,它在时间 t(秒)内离开平衡位置(就是静止时的位置)的位移 S (cm) 由 函 S = 5sin(π/2 t + π/4 ) 决定,
(1) 试求物体离开平衡位置的最大距离;
(2 试求物体往复振动一次所需的时间;
(3) 试求物体每秒钟内往复振动的次数;
解:演示课件(点击此处)
练习: (点击空白处)
练习
1、 当函数 y = -5sin (-2x +π/4) 表示一个振动量时其振幅为 周期为 ______
频率为 相位为 初相为 ;
2、将函数 y= sin2x 的图象向左平移 π/ 6 得到的曲线对应的解析式为( )
A. y=sin(2x+π/6) B. y=sin(2x-π/6)
C. y=sin(2x+π/3) D. y=sin(2x-π/3)
3、要得到函数 y = cos3x 的图象,只需将函数 y = cos (3x-π/ 6) 的图象( )
A. 向左平移π/6个单位 B. 向右平移π/6个单位
C. 向左平移π/18个单位 D. 向右平移π/18个单位
4、函数 y = 3sin( x/ 2 + π/3) 的图象可由函数 y = 3 sin x 经( )变换而得;
A. 先把横坐标扩大到原来的两倍(纵坐标不变) ,再向左平移π/6个单位
B. 先把横坐标缩短到原来的1/2倍(纵坐标不变) ,再向右平移π/3个单位
C. 先向右平移π/3个单位 ,再把横坐标缩短到原来的1/2倍(纵坐标不变)
D. 先向左平移π/3个单位 ,再把横坐标扩大到原来的两倍(纵坐标不变)
*5、要得到函数 y = cos ( 2x -π/4) 的图象,只需将函数 y = sin 2 x 的图象( )
A. 向左平移π/4个单位 B. 向右平移π / 4 个单位
C. 向左平移π/ 8个单位 D. 向右平移π/ 8个单位
5
π
1/ π
-2x +π/4
π/ 4
C
C
D
D
小结:
1、作正弦型函数y=Asin( x+ ) 的图象的方法:
(1)用“五点法”作图;
(2)利用变换关系作图。
2、函数 y = sinx 的图象与函数 y=Asin( x+ )的图象间的变换关系。
3、余弦型函数 y=Acos( x+ ) 的相关问题同样处理。
y = sinx 的图象 y=Asin( x+ )
Y = sin( x+ )
y=sin(x+ )
y=sin x
4 、 函数的物理背景
《函数y=Asin(ωx+φ)的图象》
