2020-2021学年高一数学人教A版必修2第二章2.3.1 直线与平面垂直的判定课件(共23张PPT)
文档属性
| 名称 | 2020-2021学年高一数学人教A版必修2第二章2.3.1 直线与平面垂直的判定课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 851.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 09:29:35 | ||
图片预览





文档简介
(共23张PPT)
直线与平面垂直的判定
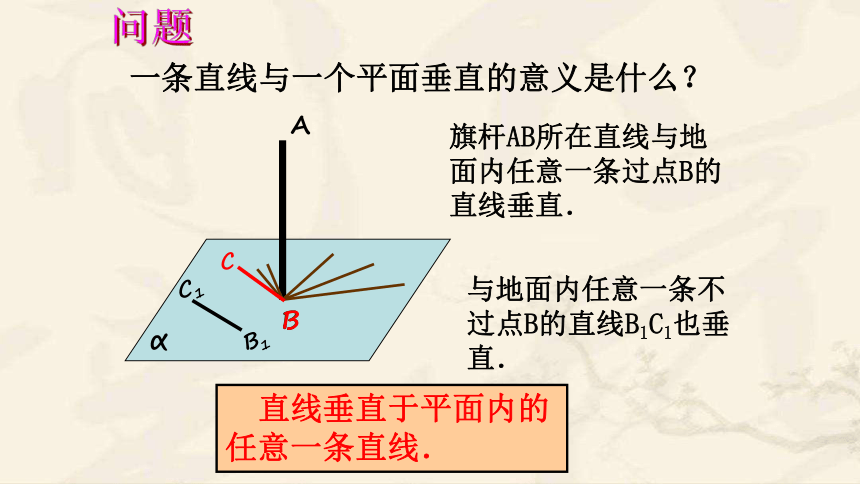
一条直线与一个平面垂直的意义是什么?
A
α
B
B1
C1
C
B
旗杆AB所在直线与地面内任意一条过点B的直线垂直.
与地面内任意一条不过点B的直线B1C1也垂直.
直线垂直于平面内的
任意一条直线.
直线与平面垂直的定义:
直线与平面的交点叫做垂足。
如果直线
与平面
内的任意一条直线都垂直,
我们就说直线
与平面
垂直,
记作
.
直线
叫做平面
的垂线,
叫做直线
平面
的垂面。
P
m
直线l与平面α垂直的画法:
通常地直线画成与表示平面的平行四边形
的一边垂直。
1.如果一条直线
l
和一个平面内的无数条直线都垂直,则直线
l
和平面
α互相垂直(
)
思考:
?
B
C
l
直线
l
垂直于平面α
,则直线
l
垂直于平面α中的任意一条直线
?
m
P
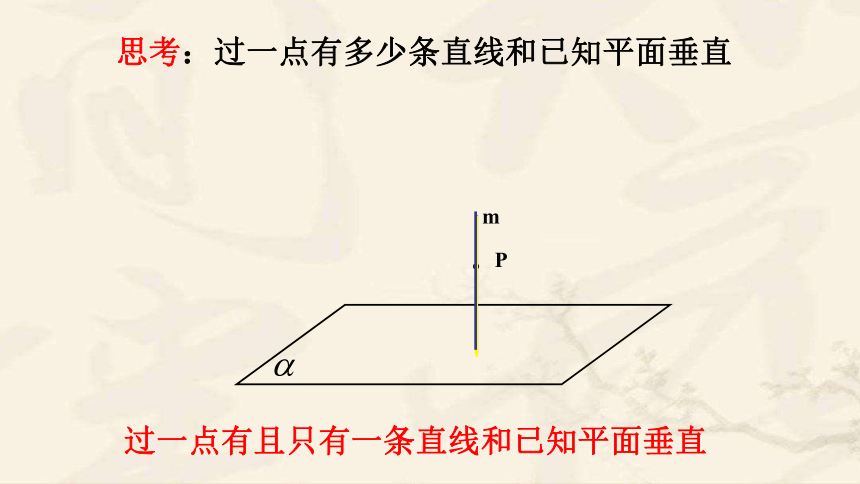
过一点有且只有一条直线和已知平面垂直
思考:过一点有多少条直线和已知平面垂直
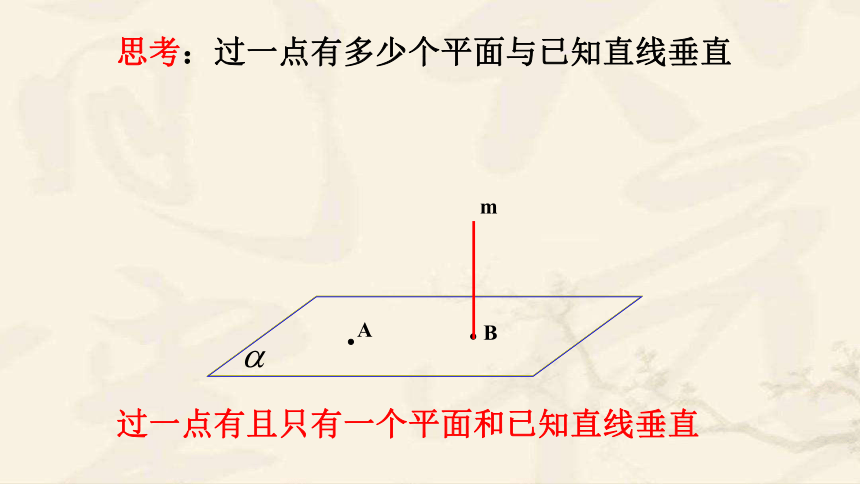
过一点有且只有一个平面和已知直线垂直
m
A
B
思考:过一点有多少个平面与已知直线垂直
除定义外,如何判定一条直线与平面垂直呢?
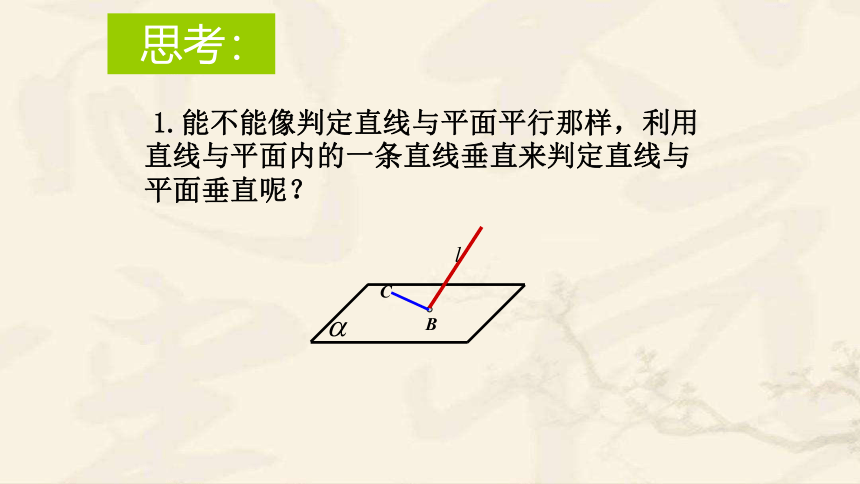
1.能不能像判定直线与平面平行那样,利用直线与平面内的一条直线垂直来判定直线与平面垂直呢?
思考:
B
C
l
2.一条直线不行,两条直线行不行呢?能利用直线l与平面内两条直线m,n都垂直来判定直线与平面垂直吗?
思考:
n
m
l
当平面内m,n平行的时候,这并不能判定l垂直于α
那平面内的两条直线相交时又是什么情况呢?
过?ABC的顶点A翻折纸片,得到折痕AD,将翻折后的纸片竖起放在桌面上(BD,DC与桌面接触)
(1)折痕AD与桌面垂直吗?
(2)如何翻折才能使折痕AD与桌面所在平面垂直?
A
B
D
C
请同学们准备一块三角形的纸片,我们一起来做一个实验:
由此你能得到什么结论呢?
一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直.
直线与平面垂直判定定理
判定定理
线线垂直
线面垂直
(1)若一条直线与一个三角形的两条边垂直,
则这条直线垂直于三角形所在的平面.(
)
(2)若一条直线与一个平行四边形的两条边
垂直,则这条直线垂直于平行四边形所在
的平面.(
)
(3)若一条直线与一个梯形的两腰垂直,则这
条直线垂直于梯形所在的平面.(
)
判断下列命题是否正确?
想一想
课本例1:
如图,已知
,求证
如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于同一个平面。
如果两条直线同时垂直于同一个平面,那么
这两条直线平行。
直线与平面垂直的性质定理
符号语言:
作用:判断两直线平行
S
B
C
D
A
E
在四棱锥S-ABCD中,SA=AB=2,SB=SD=
,底面ABCD是菱形,且∠ABC=60°,E为CD的中点
(1)证明:SA⊥面ABCD
(2)证明:AB
⊥面SAE
D1
B1
A1
C1
C
A
D
B
已知正方体ABCD-A1B1C1D1中,
求证:BD1⊥AB1
D1
B1
A1
C1
C
A
D
B
已知正方体ABCD-A1B1C1D1中,
求证:BD1⊥AB1
D1
B1
A2
C1
C
A
D
B
D1
B1
A1
C1
如图,已知PA⊥平面ABCD,且四边形ABCD为矩形,M,N分别是AB,PC的中点.
(1)求证:MN⊥CD;(2)若∠PDA=45°,求证:MN⊥平面PCD.
已知△ADB和△ADC都是以D为直角顶点的直角三角形,且AD=BD=CD,
∠BAC=60°
(1)求证:
AD⊥平面BDC
(
2)求证:BD⊥平面ADC
D
B
C
A
过△ABC所在平面
外一点P,作PO⊥
,垂足为O,连接PA,PB,PC。
若PA=PB=PC,∠C=90°
问:点O是AB边的
点
中
过△ABC所在平面
外一点P,作PO⊥
,垂足为O,连接PA,PB,PC。
若PA=PB=PC,
问:点O是△ABC的
心
外
过△ABC所在平面
外一点P,作PO⊥
,垂足为O,连接PA,PB,PC。
若PA⊥PB,PB⊥PC,PC⊥PA,
问:点O是△ABC的
心
垂
直线与平面垂直的判定
一条直线与一个平面垂直的意义是什么?
A
α
B
B1
C1
C
B
旗杆AB所在直线与地面内任意一条过点B的直线垂直.
与地面内任意一条不过点B的直线B1C1也垂直.
直线垂直于平面内的
任意一条直线.
直线与平面垂直的定义:
直线与平面的交点叫做垂足。
如果直线
与平面
内的任意一条直线都垂直,
我们就说直线
与平面
垂直,
记作
.
直线
叫做平面
的垂线,
叫做直线
平面
的垂面。
P
m
直线l与平面α垂直的画法:
通常地直线画成与表示平面的平行四边形
的一边垂直。
1.如果一条直线
l
和一个平面内的无数条直线都垂直,则直线
l
和平面
α互相垂直(
)
思考:
?
B
C
l
直线
l
垂直于平面α
,则直线
l
垂直于平面α中的任意一条直线
?
m
P
过一点有且只有一条直线和已知平面垂直
思考:过一点有多少条直线和已知平面垂直
过一点有且只有一个平面和已知直线垂直
m
A
B
思考:过一点有多少个平面与已知直线垂直
除定义外,如何判定一条直线与平面垂直呢?
1.能不能像判定直线与平面平行那样,利用直线与平面内的一条直线垂直来判定直线与平面垂直呢?
思考:
B
C
l
2.一条直线不行,两条直线行不行呢?能利用直线l与平面内两条直线m,n都垂直来判定直线与平面垂直吗?
思考:
n
m
l
当平面内m,n平行的时候,这并不能判定l垂直于α
那平面内的两条直线相交时又是什么情况呢?
过?ABC的顶点A翻折纸片,得到折痕AD,将翻折后的纸片竖起放在桌面上(BD,DC与桌面接触)
(1)折痕AD与桌面垂直吗?
(2)如何翻折才能使折痕AD与桌面所在平面垂直?
A
B
D
C
请同学们准备一块三角形的纸片,我们一起来做一个实验:
由此你能得到什么结论呢?
一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直.
直线与平面垂直判定定理
判定定理
线线垂直
线面垂直
(1)若一条直线与一个三角形的两条边垂直,
则这条直线垂直于三角形所在的平面.(
)
(2)若一条直线与一个平行四边形的两条边
垂直,则这条直线垂直于平行四边形所在
的平面.(
)
(3)若一条直线与一个梯形的两腰垂直,则这
条直线垂直于梯形所在的平面.(
)
判断下列命题是否正确?
想一想
课本例1:
如图,已知
,求证
如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于同一个平面。
如果两条直线同时垂直于同一个平面,那么
这两条直线平行。
直线与平面垂直的性质定理
符号语言:
作用:判断两直线平行
S
B
C
D
A
E
在四棱锥S-ABCD中,SA=AB=2,SB=SD=
,底面ABCD是菱形,且∠ABC=60°,E为CD的中点
(1)证明:SA⊥面ABCD
(2)证明:AB
⊥面SAE
D1
B1
A1
C1
C
A
D
B
已知正方体ABCD-A1B1C1D1中,
求证:BD1⊥AB1
D1
B1
A1
C1
C
A
D
B
已知正方体ABCD-A1B1C1D1中,
求证:BD1⊥AB1
D1
B1
A2
C1
C
A
D
B
D1
B1
A1
C1
如图,已知PA⊥平面ABCD,且四边形ABCD为矩形,M,N分别是AB,PC的中点.
(1)求证:MN⊥CD;(2)若∠PDA=45°,求证:MN⊥平面PCD.
已知△ADB和△ADC都是以D为直角顶点的直角三角形,且AD=BD=CD,
∠BAC=60°
(1)求证:
AD⊥平面BDC
(
2)求证:BD⊥平面ADC
D
B
C
A
过△ABC所在平面
外一点P,作PO⊥
,垂足为O,连接PA,PB,PC。
若PA=PB=PC,∠C=90°
问:点O是AB边的
点
中
过△ABC所在平面
外一点P,作PO⊥
,垂足为O,连接PA,PB,PC。
若PA=PB=PC,
问:点O是△ABC的
心
外
过△ABC所在平面
外一点P,作PO⊥
,垂足为O,连接PA,PB,PC。
若PA⊥PB,PB⊥PC,PC⊥PA,
问:点O是△ABC的
心
垂
