2020-2021学年七年级数学北师大版下册 1.7.1 整式的除法 课件(18张)
文档属性
| 名称 | 2020-2021学年七年级数学北师大版下册 1.7.1 整式的除法 课件(18张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 275.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-22 00:00:00 | ||
图片预览






文档简介
第一章 整式的乘除
第1课时 整式的除法
学习目标
知识点一:单项式除以单项式
(1)单项式除以单项式法则:
单项式相除,把系数、 分别相除后,作为商的因式;对于只在被除式里含有的字母,则连同它的 一起作为商的一个因式.?
指数
知识要点
同底数幂
(2)提示:单项式除以单项式法则的实质是将单项式除以单项式转化为同底数幂的除法运算,运算的结果仍是单项式.举例如下:
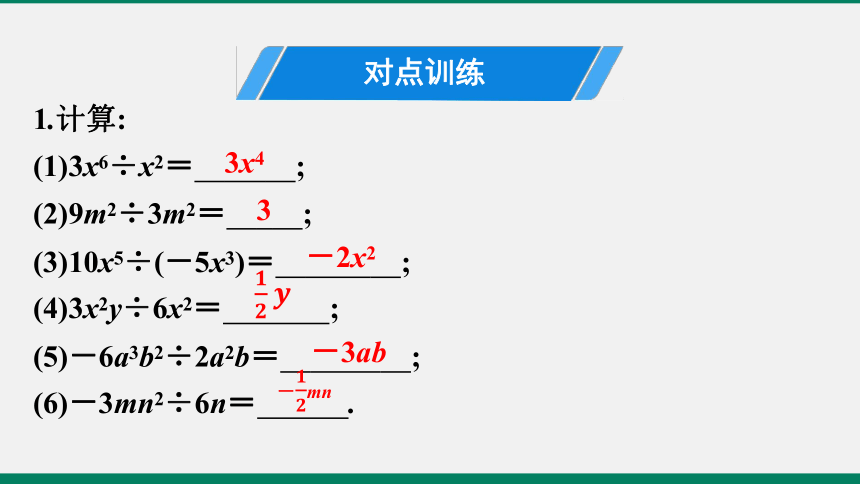
1.计算:
(1)3x6÷x2= ;?
(2)9m2÷3m2= ;?
(3)10x5÷(-5x3)= ;?
(4)3x2y÷6x2=? ;?
(5)-6a3b2÷2a2b= ;?
(6)-3mn2÷6n= .?
-3ab
-2x2
3
对点训练
3x4
-????????mn
?
????????????
?
知识点二:单项式除以单项式的一般步骤
?
(1)系数:把系数相除,所得结果作为商的系数.注意单项式的系数包含它前面的符号;
?
(2)同底数幂:把同底数幂相除,所得结果作为商的因式;
(3)只在被除式里含有的字母,则连同它的指数一起作为商的一个因式.
2.计算:
(1)24a3b2 ÷ 3ab2;
解:(1)原式=(24÷3)(a3÷a)(b2÷b2)
=8a3-1·1
=8a2.
(2)-21a2b3c ÷ 3ab.
(2)原式=(-21÷3)a2-1b3-1c
=-7ab2c.
知识点三:整式的混合运算
?
解题时要注意运算顺序,先乘方,再乘除.有括号先算括号内的,同级运算按照从左到右的顺序进行.
3.计算:
(1)(6xy2)2 ÷ 3xy;
解:(1)原式=36x2y4÷3xy=12xy3.
4.计算(a4b)2 ÷ a2的结果是( )
A.a2b2 B.a6b2
C.a7b2 D.a8b2
精典范例
B
5.计算(-6xy2)2 ÷(-3xy)的结果为( )
A.-12xy3 B.2y3
C.12xy D.2xy3
变式练习
A
6.计算:
(1)12a3b2 ÷ 3ab; (2)-8xy2 ÷ 2xy;
4a2b -4y
7.计算:
(1)2x2y3 ÷(-3xy); (2)10x2y3 ÷ 2x2y;
8.计算:6xy2·(-2x2y) ÷(-3y3).
解:原式=-12x3y3÷(-3y3)=4x3.
9.计算:(-3x2y)2·6xy3 ÷ 9x3y4.
解:原式=9x4y2·6xy3÷9x3y4=54x5y5÷9x3y4=6x2y.
10.已知8a3bm ÷ 8anb2=b2,那么m,n的取值为( )
A.m=4,n=3 B.m=4,n=1
C.m=1,n=3 D.m=2,n=3
A
11.(新题速递)(2020河北)墨迹覆盖了等式“x3 x=x2(x≠0)”中的运算符号,则覆盖的是( )
A.+
B.-
C.×
D.÷
D
★12.(创新题)在一次“学数学,用少年智力开发报”的主题会上,有这样一个节目:主持人小明同学亮出了A,B,C三张卡片,上面分别写有16a3b4c2 ,4a2bc ,32a4b7c3 ,其中有两张卡片上的单项式相除,所得的商为2ab3c.这两张卡片是 和 ,作为被除式的卡片是 (只填写卡片代号即可).?
C
A
C
第1课时 整式的除法
学习目标
知识点一:单项式除以单项式
(1)单项式除以单项式法则:
单项式相除,把系数、 分别相除后,作为商的因式;对于只在被除式里含有的字母,则连同它的 一起作为商的一个因式.?
指数
知识要点
同底数幂
(2)提示:单项式除以单项式法则的实质是将单项式除以单项式转化为同底数幂的除法运算,运算的结果仍是单项式.举例如下:
1.计算:
(1)3x6÷x2= ;?
(2)9m2÷3m2= ;?
(3)10x5÷(-5x3)= ;?
(4)3x2y÷6x2=? ;?
(5)-6a3b2÷2a2b= ;?
(6)-3mn2÷6n= .?
-3ab
-2x2
3
对点训练
3x4
-????????mn
?
????????????
?
知识点二:单项式除以单项式的一般步骤
?
(1)系数:把系数相除,所得结果作为商的系数.注意单项式的系数包含它前面的符号;
?
(2)同底数幂:把同底数幂相除,所得结果作为商的因式;
(3)只在被除式里含有的字母,则连同它的指数一起作为商的一个因式.
2.计算:
(1)24a3b2 ÷ 3ab2;
解:(1)原式=(24÷3)(a3÷a)(b2÷b2)
=8a3-1·1
=8a2.
(2)-21a2b3c ÷ 3ab.
(2)原式=(-21÷3)a2-1b3-1c
=-7ab2c.
知识点三:整式的混合运算
?
解题时要注意运算顺序,先乘方,再乘除.有括号先算括号内的,同级运算按照从左到右的顺序进行.
3.计算:
(1)(6xy2)2 ÷ 3xy;
解:(1)原式=36x2y4÷3xy=12xy3.
4.计算(a4b)2 ÷ a2的结果是( )
A.a2b2 B.a6b2
C.a7b2 D.a8b2
精典范例
B
5.计算(-6xy2)2 ÷(-3xy)的结果为( )
A.-12xy3 B.2y3
C.12xy D.2xy3
变式练习
A
6.计算:
(1)12a3b2 ÷ 3ab; (2)-8xy2 ÷ 2xy;
4a2b -4y
7.计算:
(1)2x2y3 ÷(-3xy); (2)10x2y3 ÷ 2x2y;
8.计算:6xy2·(-2x2y) ÷(-3y3).
解:原式=-12x3y3÷(-3y3)=4x3.
9.计算:(-3x2y)2·6xy3 ÷ 9x3y4.
解:原式=9x4y2·6xy3÷9x3y4=54x5y5÷9x3y4=6x2y.
10.已知8a3bm ÷ 8anb2=b2,那么m,n的取值为( )
A.m=4,n=3 B.m=4,n=1
C.m=1,n=3 D.m=2,n=3
A
11.(新题速递)(2020河北)墨迹覆盖了等式“x3 x=x2(x≠0)”中的运算符号,则覆盖的是( )
A.+
B.-
C.×
D.÷
D
★12.(创新题)在一次“学数学,用少年智力开发报”的主题会上,有这样一个节目:主持人小明同学亮出了A,B,C三张卡片,上面分别写有16a3b4c2 ,4a2bc ,32a4b7c3 ,其中有两张卡片上的单项式相除,所得的商为2ab3c.这两张卡片是 和 ,作为被除式的卡片是 (只填写卡片代号即可).?
C
A
C
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
