2020-2021学年七年级数学华东师大版下册6.2.1等式的性质与方程的简单变形课件(共18张)
文档属性
| 名称 | 2020-2021学年七年级数学华东师大版下册6.2.1等式的性质与方程的简单变形课件(共18张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 344.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-22 13:31:20 | ||
图片预览






文档简介
6.2解一元一次方程
义务教育课程标准实验教科书
七年级 下册
学习目标
1.理解方程简单变形的依据与方法。
2.通过实例感受方程变形的合理性。
3.会用方程变形解简单的一元一次方程。
重点、难点
重点:理解方程简单变形的依据与方法。
难点:如何用方程变形解简单的一元一次方程。
小刚在做作业时,遇到方程
2x=5x,他将方程两边同时
除以x,竟然得到2=5!他错
在什么地方?
请你判断
等式的基本性质是什么?
探究新知
你用过天平吗?用天平称物,有什么特点?
方程和平天平有相似之处吗?
学习课本第4页,总结方程的变形法则!
归纳总结
等式性质1:方程两边都加上或减去同一个数或同一个整式,
方程的解不变;
等式性质2:方程两边都乘以或除以同一个不为零的数,
方程的解不变。
通过对方程进行适当的变形,可以求得方程
的解。
看 谁 解 得 快
解方程: 5x – 2 = 8 .
解:
得
方程
5x – 2 = 8
两边同时加上 2 ,
5x – 2 = 8
+ 2
+ 2
即 5x =
10
两边同除以5 得:
x = 2.
?
5x = 8 + 2
为什么?
把原求解的书写格式改成:
5x – 2 = 8
5x = 8 + 2
简缩格式:
有什么规律可循?
5x – 2 + 2 = 8 + 2
能否写成:
解题后的思考
?
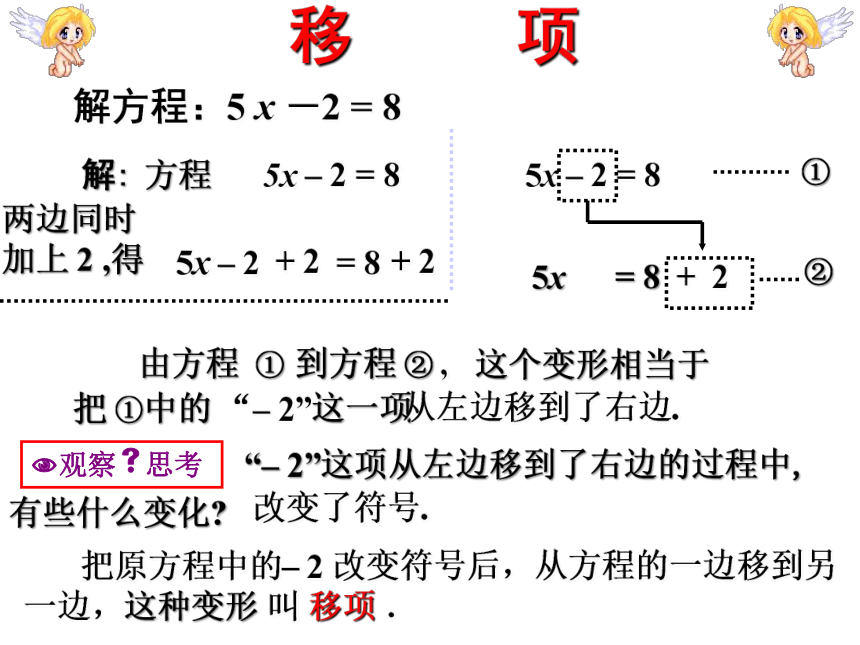
移 项
解方程:5 x -2 = 8
解:
方程
5x – 2 = 8
两边同时
加上 2 ,得
5x – 2 = 8
+ 2
+ 2
5x – 2 = 8
5x = 8 + 2
这个变形相当于
把 ①中的 “– 2”这一项
由方程 ①
①
到方程 ② ,
②
从左边移到了右边.
?观察?思考
“– 2”这项从左边移到了右边的过程中,
有些什么变化?
改变了符号.
把原方程中的– 2 改变符号后,从方程的一边移到另
一边,这种变形 叫 移项 .
移 项
例1
(1)x-5=7
解:(1)由x-5=7
(2)4x=3x-4
移项,得
即
x=12
解:(2)由4x=3x-4
移项,得
x=7+5
4x-3x=-4
即
x=-4
在上面的解方程过程中,移项一定要变号!
解下列方程:
方程两边都乘以或除以同一个不为零的数,
方程的解不变。
两边都除以-5,得
解下列方程:
例2
上面两种方程都是“将未知数的系数化为1”。
请问如何“将未知数的系数化为1”?
利用方程的变形求方程 的解
请说出每一步的变形
( )
( )
移项
将x的系数化为1
做一做
例题解析
在前面的解方程中,移项后的“化简”只用到了对常项的合并。
试看看下述的解方程。
例3 解下列方程:
(1)8x=2x-7
(2)6=8+2x
(3)
? 观察 & 思考 ?
① 移项有什么新特点?
② 移项后的化简包括哪些内容?
含未知数的项宜向左移、常数项往右移.
左边对含未知数的项合并、右边对常数项合并.
解方程的思考途径
例3 解下列方程:
(1)8x=2x-7
(2)6=8+2x
(3)
解:8x=2x-7
移项,得
8x-2x=-7
合并同类项,得6x=-7
将x的系数化为1,得
试一试,你会解(2)、(3)
小题吗?
含未知数的项宜向左移、常数项向右移。左边对含未知数的项合并、右边对常数项合并。
解法欣赏
解法欣赏
解 题 后 的 反 思
(1) 移项实际上是对方程两边进行 ,
使用的是等式的性质 ;
? 解题后的反思
(2) 系数 化为 1 实际上是对方程两边进行 ,
使用的是等式的性质 .
同乘除
同加减
1
2
1.下列方程变形是否正确?为什么?
牛 刀 小 试
2.解下列方程。
我们的收获……
结合本堂课的内容,请用下列句式造句。
我学会了……
我明白了……
我认为……
我会用……
我想……
义务教育课程标准实验教科书
七年级 下册
学习目标
1.理解方程简单变形的依据与方法。
2.通过实例感受方程变形的合理性。
3.会用方程变形解简单的一元一次方程。
重点、难点
重点:理解方程简单变形的依据与方法。
难点:如何用方程变形解简单的一元一次方程。
小刚在做作业时,遇到方程
2x=5x,他将方程两边同时
除以x,竟然得到2=5!他错
在什么地方?
请你判断
等式的基本性质是什么?
探究新知
你用过天平吗?用天平称物,有什么特点?
方程和平天平有相似之处吗?
学习课本第4页,总结方程的变形法则!
归纳总结
等式性质1:方程两边都加上或减去同一个数或同一个整式,
方程的解不变;
等式性质2:方程两边都乘以或除以同一个不为零的数,
方程的解不变。
通过对方程进行适当的变形,可以求得方程
的解。
看 谁 解 得 快
解方程: 5x – 2 = 8 .
解:
得
方程
5x – 2 = 8
两边同时加上 2 ,
5x – 2 = 8
+ 2
+ 2
即 5x =
10
两边同除以5 得:
x = 2.
?
5x = 8 + 2
为什么?
把原求解的书写格式改成:
5x – 2 = 8
5x = 8 + 2
简缩格式:
有什么规律可循?
5x – 2 + 2 = 8 + 2
能否写成:
解题后的思考
?
移 项
解方程:5 x -2 = 8
解:
方程
5x – 2 = 8
两边同时
加上 2 ,得
5x – 2 = 8
+ 2
+ 2
5x – 2 = 8
5x = 8 + 2
这个变形相当于
把 ①中的 “– 2”这一项
由方程 ①
①
到方程 ② ,
②
从左边移到了右边.
?观察?思考
“– 2”这项从左边移到了右边的过程中,
有些什么变化?
改变了符号.
把原方程中的– 2 改变符号后,从方程的一边移到另
一边,这种变形 叫 移项 .
移 项
例1
(1)x-5=7
解:(1)由x-5=7
(2)4x=3x-4
移项,得
即
x=12
解:(2)由4x=3x-4
移项,得
x=7+5
4x-3x=-4
即
x=-4
在上面的解方程过程中,移项一定要变号!
解下列方程:
方程两边都乘以或除以同一个不为零的数,
方程的解不变。
两边都除以-5,得
解下列方程:
例2
上面两种方程都是“将未知数的系数化为1”。
请问如何“将未知数的系数化为1”?
利用方程的变形求方程 的解
请说出每一步的变形
( )
( )
移项
将x的系数化为1
做一做
例题解析
在前面的解方程中,移项后的“化简”只用到了对常项的合并。
试看看下述的解方程。
例3 解下列方程:
(1)8x=2x-7
(2)6=8+2x
(3)
? 观察 & 思考 ?
① 移项有什么新特点?
② 移项后的化简包括哪些内容?
含未知数的项宜向左移、常数项往右移.
左边对含未知数的项合并、右边对常数项合并.
解方程的思考途径
例3 解下列方程:
(1)8x=2x-7
(2)6=8+2x
(3)
解:8x=2x-7
移项,得
8x-2x=-7
合并同类项,得6x=-7
将x的系数化为1,得
试一试,你会解(2)、(3)
小题吗?
含未知数的项宜向左移、常数项向右移。左边对含未知数的项合并、右边对常数项合并。
解法欣赏
解法欣赏
解 题 后 的 反 思
(1) 移项实际上是对方程两边进行 ,
使用的是等式的性质 ;
? 解题后的反思
(2) 系数 化为 1 实际上是对方程两边进行 ,
使用的是等式的性质 .
同乘除
同加减
1
2
1.下列方程变形是否正确?为什么?
牛 刀 小 试
2.解下列方程。
我们的收获……
结合本堂课的内容,请用下列句式造句。
我学会了……
我明白了……
我认为……
我会用……
我想……
