苏科版八年级下册数学 假期练习题:第11章 反比例函数(Word版 含答案)
文档属性
| 名称 | 苏科版八年级下册数学 假期练习题:第11章 反比例函数(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 196.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-22 12:42:17 | ||
图片预览

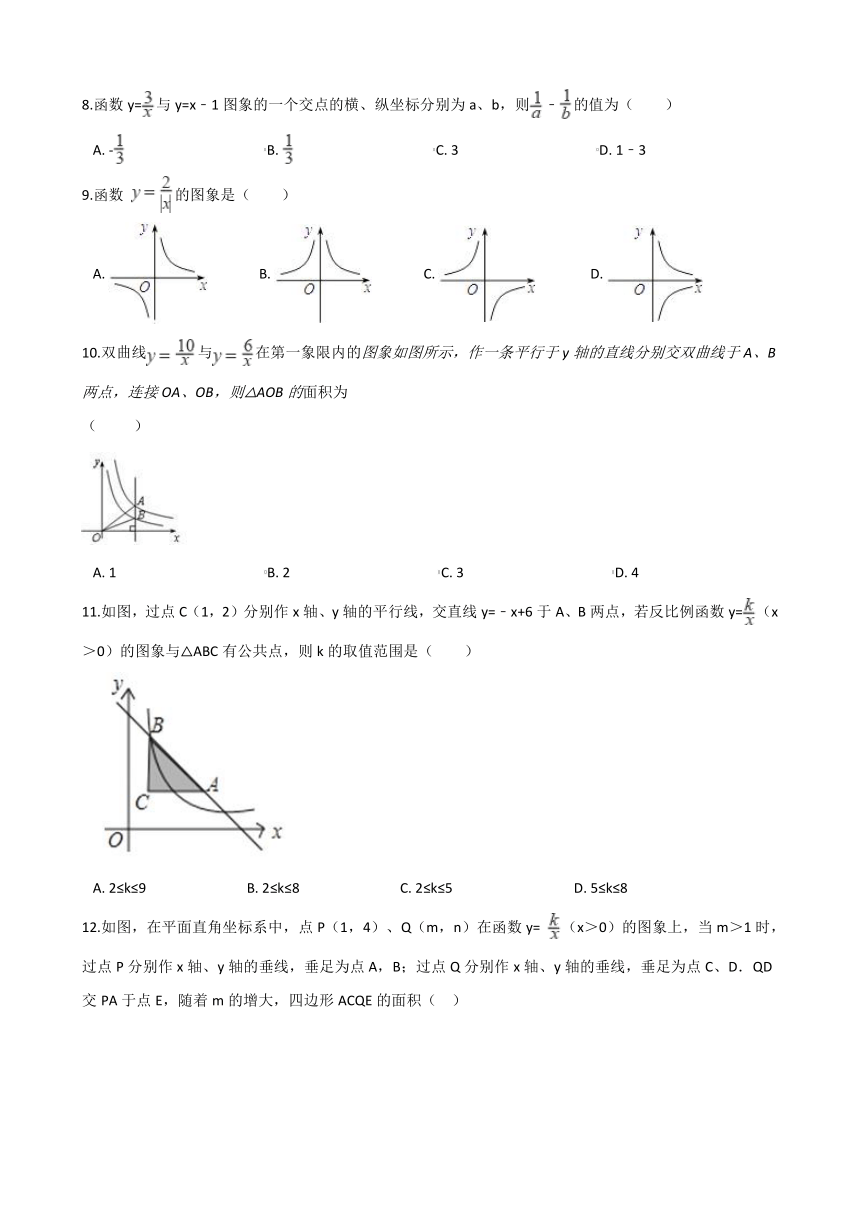

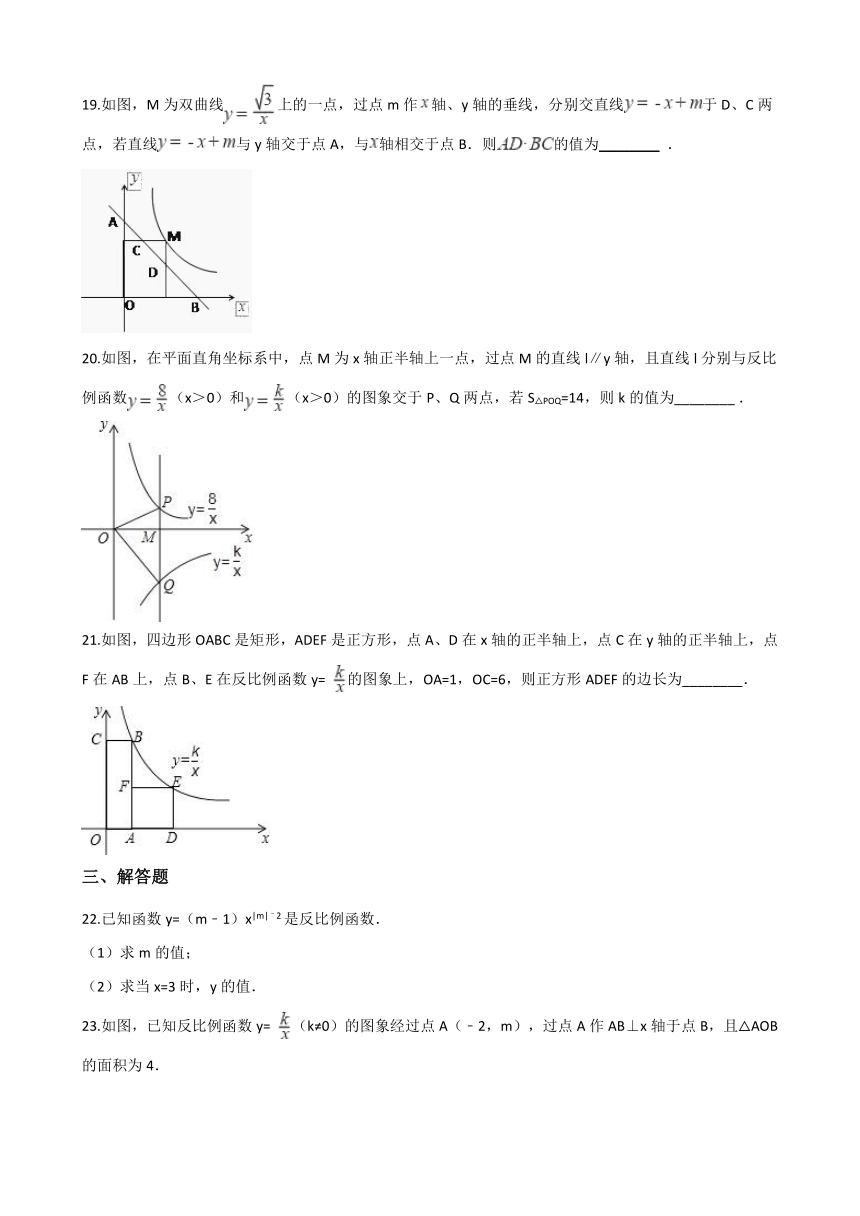

文档简介
第11章 反比例函数
一、选择题
1.下列函数中,y是x的反比例函数的是(?? )
A.?y= ???????????????????????????????B.?y= ???????????????????????????????C.?y= ???????????????????????????????D.?y=﹣
2.已知反比例函数的图象经过点(2,﹣1),则它的解析式是( )
A.?y=﹣2x???????????????????????????????B.?y=2x???????????????????????????????C.????????????????????????????????D.?
3.已知反比例函数, 下列结论不正确的是( ? ?? )
A.?图象经过点(1,1)??????????????????????????????????????????B.?图象在第一、三象限
C.?当x>1时,04.若反比例函数y=的图象位于第二、四象限,则k的取值可能是( )
A.?-1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
5.如图,所示的计算程序中,y与x之间的函数关系对应的图象所在的象限是(?????? )
A.?第一象限????????????????????B.?第一、三象限????????????????????C.?第二、四象限????????????????????D.?第一、四象限
6.如图,反比例函数 的图象经过点A,则当x=﹣1时,y的值是(?? )
A.?2?????????????????????????????????????????B.?﹣2?????????????????????????????????????????C.??????????????????????????????????????????D.?-
7.反比例函数 的大致图象为(?? )
A.????????????????B.????????????????C.????????????????D.?
8.函数y=与y=x﹣1图象的一个交点的横、纵坐标分别为a、b,则﹣的值为( )
A.?-????????????????????????????????????????B.?????????????????????????????????????????C.?3????????????????????????????????????????D.?1﹣3
9.函数 的图象是( )
A.????????????????B.????????????????C.?????????????????D.?
10.双曲线与在第一象限内的图象如图所示,作一条平行于y轴的直线分别交双曲线于A、B两点,连接OA、OB,则△AOB的面积为
(?? ? ? )
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
11.如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=﹣x+6于A、B两点,若反比例函数y=(x>0)的图象与△ABC有公共点,则k的取值范围是( )
?
A.?2≤k≤9?????????????????????????????B.?2≤k≤8?????????????????????????????C.?2≤k≤5???????????????????????????????????D.?5≤k≤8
12.如图,在平面直角坐标系中,点P(1,4)、Q(m,n)在函数y= (x>0)的图象上,当m>1时,过点P分别作x轴、y轴的垂线,垂足为点A,B;过点Q分别作x轴、y轴的垂线,垂足为点C、D.QD交PA于点E,随着m的增大,四边形ACQE的面积(?? )
A.?减小???????????????????????????B.?增大???????????????????????????C.?先减小后增大???????????????????????????D.?先增大后减小
二、填空题
13.若函数 是反比例函数,则其表达式是________.
14.已知反比例函数 的图象位于第一、三象限,则 的取值范围是________.
15.已知一次函数y=3x+m与反比例函数y=的图象有两个交点,当m=________?时,有一个交点的纵坐标为6.
16.已知点P(1,2)在反比例函数 的图象上,根据图象判断,当x>1时,y的取值范围是________
17.某人用所带的钱去买某种每支售价1.8元的圆珠笔,恰好买12支,假设他用这些钱可买单价为x元的圆珠笔y支,那么y与x的函数关系式为________.
18.反比例函数y=的图象如图所示,点M是该图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=3,则k的值为________.?
19.如图,M为双曲线上的一点,过点m作轴、y轴的垂线,分别交直线于D、C两点,若直线与y轴交于点A,与轴相交于点B.则的值为________ .
20.如图,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线l∥y轴,且直线l分别与反比例函数(x>0)和(x>0)的图象交于P、Q两点,若S△POQ=14,则k的值为________?.
21.如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y= 的图象上,OA=1,OC=6,则正方形ADEF的边长为________.
三、解答题
22.已知函数y=(m﹣1)x|m|﹣2是反比例函数.
(1)求m的值;
(2)求当x=3时,y的值.
23.如图,已知反比例函数y= (k≠0)的图象经过点A(﹣2,m),过点A作AB⊥x轴于点B,且△AOB的面积为4.
(Ⅰ)求k和m的值;
(Ⅱ)设C(x,y)是该反比例函数图象上一点,当1≤x≤4时,求函数值y的取值范围.
24.反比例函数(k≠0)与一次函数y=mx+b(m≠0)交于点A(1,2k﹣1).
(1)求反比例函数的解析式;
(2)若一次函数与x轴交于点B,且△AOB的面积为3,求一次函数的解析式.
25.如图,直线y=x﹣1与反比例函数y= 的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(﹣1,m).
(1)求反比例函数的解析式;
(2)若点P(n,﹣1)是反比例函数图象上一点,过点P作PE⊥x轴于点E,延长EP交直线AB于点F,求△CEF的面积.
26.如图,已知A(﹣4,a),B(﹣1,2)是一次函数y1=kx+b与反比例函数y2= (m<0)图象的两个交点,AC⊥x轴于C.
(1)求出k,b及m的值.
(2)根据图象直接回答:在第二象限内,当y1>y2时,x的取值范围是 ________.
(3)若P是线段AB上的一点,连接PC,若△PCA的面积等于 ,求点P坐标.
27.如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2= (m为常数,且m≠0)的图象交于点A(﹣2,1)、B(1,n).
(1)求反比例函数和一次函数的解析式;
(2)连结OA、OB,求△AOB的面积;
(3)直接写出当y1<y2<0时,自变量x的取值范围.
参考答案
一、选择题
1.D 2. D 3. D 4. A 5. C 6.A 7. C 8. A 9. B 10. B 11. A 12.B
二、填空题
13. 14. 15.5 16.0<y<2
17.y= 18.-3 19. 20.-20 21.2
三、解答题
22.解:(1)|m|﹣2=﹣1且m﹣1≠0,
解得:m=±1且m≠1,
∴m=﹣1.
(2)当m=﹣1时,原方程变为y=﹣,
当x=3时,y=﹣.
23.解:(Ⅰ)∵△AOB的面积为4,
∴ ?(?xA)?yA=4,
即可得:k=xA?yA=﹣8,
令x=2,得:m=4;
(Ⅱ)当1≤x≤4时,y随x的增大而增大,
令x=1,得:y=﹣8;
令x=4,得:y=﹣2,
所以﹣8≤y≤﹣2即为所求.
24.(1)解:把A(1,2k﹣1)代入得,
2k﹣1=k,
∴k=1,
∴反比例函数的解析式为:;
(2)解:由(1)得k=1,
∴A(1,1),
设B(a,0),
∴S△AOB=?|a|×1=3,
∴a=±6,
∴B(﹣6,0)或(6,0),
把A(1,1),B(﹣6,0)代入y=mx+b得:,
∴,
∴一次函数的解析式为:,
把A(1,1),B(6,0)代入y=mx+b得:,
∴,
∴一次函数的解析式为:.
所以符合条件的一次函数解析式为或.
25.(1)解:将点A的坐标代入y=x﹣1,可得:m=﹣1﹣1=﹣2, 将点A(﹣1,﹣2)代入反比例函数y= ,可得:k=﹣1×(﹣2)=2,
故反比例函数解析式为:y=
(2)解:将点P的纵坐标y=﹣1,代入反比例函数关系式可得:x=﹣2, 将点F的横坐标x=﹣2代入直线解析式可得:y=﹣3,
故可得EF=3,CE=OE+OC=2+1=3,
故可得S△CEF= CE×EF=
26.(1)解:把B(﹣1,2)代入y= 得m=﹣1×2=﹣2,
把A(﹣4,a)代入y=﹣ 得a=﹣ = ,
把A(﹣4, ),B(﹣1,2)代入y=kx+b,
得 ,
解得: ,
∴k= ?,b= ,m=﹣2
(2)﹣4<x<﹣1
(3)解:设点P的横坐标为xP ,
∵AC⊥x轴,点A(﹣4, ),
∴AC= .
∵△PCA的面积等于 ,
∴ × ×[xP﹣(﹣4)]= ,
解得xP=﹣2,
∵P是线段AB上的一点,
∴yP= ×(﹣2)+ = ,
∴点P的坐标为(﹣2, ?)
27. (1)解:∵A(﹣2,1),
∴将A坐标代入反比例函数解析式y2= 中,得m=﹣2,
∴反比例函数解析式为y=﹣ ;
将B坐标代入y=﹣ ,得n=﹣2,
∴B坐标(1,﹣2),
将A与B坐标代入一次函数解析式中,得 ,
解得a=﹣1,b=﹣1,
∴一次函数解析式为y1=﹣x﹣1
(2)解:设直线AB与y轴交于点C,
令x=0,得y=﹣1,
∴点C坐标(0,﹣1),
∴S△AOB=S△AOC+S△COB= ×1×2+ ×1×1=
(3)解:由图象可得,当y1<y2<0时,自变量x的取值范围x>1.
一、选择题
1.下列函数中,y是x的反比例函数的是(?? )
A.?y= ???????????????????????????????B.?y= ???????????????????????????????C.?y= ???????????????????????????????D.?y=﹣
2.已知反比例函数的图象经过点(2,﹣1),则它的解析式是( )
A.?y=﹣2x???????????????????????????????B.?y=2x???????????????????????????????C.????????????????????????????????D.?
3.已知反比例函数, 下列结论不正确的是( ? ?? )
A.?图象经过点(1,1)??????????????????????????????????????????B.?图象在第一、三象限
C.?当x>1时,0
A.?-1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
5.如图,所示的计算程序中,y与x之间的函数关系对应的图象所在的象限是(?????? )
A.?第一象限????????????????????B.?第一、三象限????????????????????C.?第二、四象限????????????????????D.?第一、四象限
6.如图,反比例函数 的图象经过点A,则当x=﹣1时,y的值是(?? )
A.?2?????????????????????????????????????????B.?﹣2?????????????????????????????????????????C.??????????????????????????????????????????D.?-
7.反比例函数 的大致图象为(?? )
A.????????????????B.????????????????C.????????????????D.?
8.函数y=与y=x﹣1图象的一个交点的横、纵坐标分别为a、b,则﹣的值为( )
A.?-????????????????????????????????????????B.?????????????????????????????????????????C.?3????????????????????????????????????????D.?1﹣3
9.函数 的图象是( )
A.????????????????B.????????????????C.?????????????????D.?
10.双曲线与在第一象限内的图象如图所示,作一条平行于y轴的直线分别交双曲线于A、B两点,连接OA、OB,则△AOB的面积为
(?? ? ? )
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
11.如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=﹣x+6于A、B两点,若反比例函数y=(x>0)的图象与△ABC有公共点,则k的取值范围是( )
?
A.?2≤k≤9?????????????????????????????B.?2≤k≤8?????????????????????????????C.?2≤k≤5???????????????????????????????????D.?5≤k≤8
12.如图,在平面直角坐标系中,点P(1,4)、Q(m,n)在函数y= (x>0)的图象上,当m>1时,过点P分别作x轴、y轴的垂线,垂足为点A,B;过点Q分别作x轴、y轴的垂线,垂足为点C、D.QD交PA于点E,随着m的增大,四边形ACQE的面积(?? )
A.?减小???????????????????????????B.?增大???????????????????????????C.?先减小后增大???????????????????????????D.?先增大后减小
二、填空题
13.若函数 是反比例函数,则其表达式是________.
14.已知反比例函数 的图象位于第一、三象限,则 的取值范围是________.
15.已知一次函数y=3x+m与反比例函数y=的图象有两个交点,当m=________?时,有一个交点的纵坐标为6.
16.已知点P(1,2)在反比例函数 的图象上,根据图象判断,当x>1时,y的取值范围是________
17.某人用所带的钱去买某种每支售价1.8元的圆珠笔,恰好买12支,假设他用这些钱可买单价为x元的圆珠笔y支,那么y与x的函数关系式为________.
18.反比例函数y=的图象如图所示,点M是该图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=3,则k的值为________.?
19.如图,M为双曲线上的一点,过点m作轴、y轴的垂线,分别交直线于D、C两点,若直线与y轴交于点A,与轴相交于点B.则的值为________ .
20.如图,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线l∥y轴,且直线l分别与反比例函数(x>0)和(x>0)的图象交于P、Q两点,若S△POQ=14,则k的值为________?.
21.如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y= 的图象上,OA=1,OC=6,则正方形ADEF的边长为________.
三、解答题
22.已知函数y=(m﹣1)x|m|﹣2是反比例函数.
(1)求m的值;
(2)求当x=3时,y的值.
23.如图,已知反比例函数y= (k≠0)的图象经过点A(﹣2,m),过点A作AB⊥x轴于点B,且△AOB的面积为4.
(Ⅰ)求k和m的值;
(Ⅱ)设C(x,y)是该反比例函数图象上一点,当1≤x≤4时,求函数值y的取值范围.
24.反比例函数(k≠0)与一次函数y=mx+b(m≠0)交于点A(1,2k﹣1).
(1)求反比例函数的解析式;
(2)若一次函数与x轴交于点B,且△AOB的面积为3,求一次函数的解析式.
25.如图,直线y=x﹣1与反比例函数y= 的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(﹣1,m).
(1)求反比例函数的解析式;
(2)若点P(n,﹣1)是反比例函数图象上一点,过点P作PE⊥x轴于点E,延长EP交直线AB于点F,求△CEF的面积.
26.如图,已知A(﹣4,a),B(﹣1,2)是一次函数y1=kx+b与反比例函数y2= (m<0)图象的两个交点,AC⊥x轴于C.
(1)求出k,b及m的值.
(2)根据图象直接回答:在第二象限内,当y1>y2时,x的取值范围是 ________.
(3)若P是线段AB上的一点,连接PC,若△PCA的面积等于 ,求点P坐标.
27.如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2= (m为常数,且m≠0)的图象交于点A(﹣2,1)、B(1,n).
(1)求反比例函数和一次函数的解析式;
(2)连结OA、OB,求△AOB的面积;
(3)直接写出当y1<y2<0时,自变量x的取值范围.
参考答案
一、选择题
1.D 2. D 3. D 4. A 5. C 6.A 7. C 8. A 9. B 10. B 11. A 12.B
二、填空题
13. 14. 15.5 16.0<y<2
17.y= 18.-3 19. 20.-20 21.2
三、解答题
22.解:(1)|m|﹣2=﹣1且m﹣1≠0,
解得:m=±1且m≠1,
∴m=﹣1.
(2)当m=﹣1时,原方程变为y=﹣,
当x=3时,y=﹣.
23.解:(Ⅰ)∵△AOB的面积为4,
∴ ?(?xA)?yA=4,
即可得:k=xA?yA=﹣8,
令x=2,得:m=4;
(Ⅱ)当1≤x≤4时,y随x的增大而增大,
令x=1,得:y=﹣8;
令x=4,得:y=﹣2,
所以﹣8≤y≤﹣2即为所求.
24.(1)解:把A(1,2k﹣1)代入得,
2k﹣1=k,
∴k=1,
∴反比例函数的解析式为:;
(2)解:由(1)得k=1,
∴A(1,1),
设B(a,0),
∴S△AOB=?|a|×1=3,
∴a=±6,
∴B(﹣6,0)或(6,0),
把A(1,1),B(﹣6,0)代入y=mx+b得:,
∴,
∴一次函数的解析式为:,
把A(1,1),B(6,0)代入y=mx+b得:,
∴,
∴一次函数的解析式为:.
所以符合条件的一次函数解析式为或.
25.(1)解:将点A的坐标代入y=x﹣1,可得:m=﹣1﹣1=﹣2, 将点A(﹣1,﹣2)代入反比例函数y= ,可得:k=﹣1×(﹣2)=2,
故反比例函数解析式为:y=
(2)解:将点P的纵坐标y=﹣1,代入反比例函数关系式可得:x=﹣2, 将点F的横坐标x=﹣2代入直线解析式可得:y=﹣3,
故可得EF=3,CE=OE+OC=2+1=3,
故可得S△CEF= CE×EF=
26.(1)解:把B(﹣1,2)代入y= 得m=﹣1×2=﹣2,
把A(﹣4,a)代入y=﹣ 得a=﹣ = ,
把A(﹣4, ),B(﹣1,2)代入y=kx+b,
得 ,
解得: ,
∴k= ?,b= ,m=﹣2
(2)﹣4<x<﹣1
(3)解:设点P的横坐标为xP ,
∵AC⊥x轴,点A(﹣4, ),
∴AC= .
∵△PCA的面积等于 ,
∴ × ×[xP﹣(﹣4)]= ,
解得xP=﹣2,
∵P是线段AB上的一点,
∴yP= ×(﹣2)+ = ,
∴点P的坐标为(﹣2, ?)
27. (1)解:∵A(﹣2,1),
∴将A坐标代入反比例函数解析式y2= 中,得m=﹣2,
∴反比例函数解析式为y=﹣ ;
将B坐标代入y=﹣ ,得n=﹣2,
∴B坐标(1,﹣2),
将A与B坐标代入一次函数解析式中,得 ,
解得a=﹣1,b=﹣1,
∴一次函数解析式为y1=﹣x﹣1
(2)解:设直线AB与y轴交于点C,
令x=0,得y=﹣1,
∴点C坐标(0,﹣1),
∴S△AOB=S△AOC+S△COB= ×1×2+ ×1×1=
(3)解:由图象可得,当y1<y2<0时,自变量x的取值范围x>1.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
