2020-2021学年人教版九年级数学下册第27章《相似》常考题型综合练习一( word版含答案)
文档属性
| 名称 | 2020-2021学年人教版九年级数学下册第27章《相似》常考题型综合练习一( word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 226.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-22 12:36:19 | ||
图片预览


文档简介
九年级数学下册第27章《相似》常考题型综合练习一
1.如图所示,在等腰△ABC中,AB=AC=10cm,BC=16cm.点D由点A出发沿AB方向向点B匀速运动,同时点E由点B出发沿BC方向向点C匀速运动,它们的速度均为1cm/s.连接DE,设运动时间为t(s)(0<t<10),解答下列问题:
(1)当t为何值时,△BDE的面积为7.5cm2;
(2)在点D,E的运动中,是否存在时间t,使得△BDE与△ABC相似?若存在,请求出对应的时间t;若不存在,请说明理由.
2.如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)连接AQ、CP,若AQ⊥CP,求t的值.
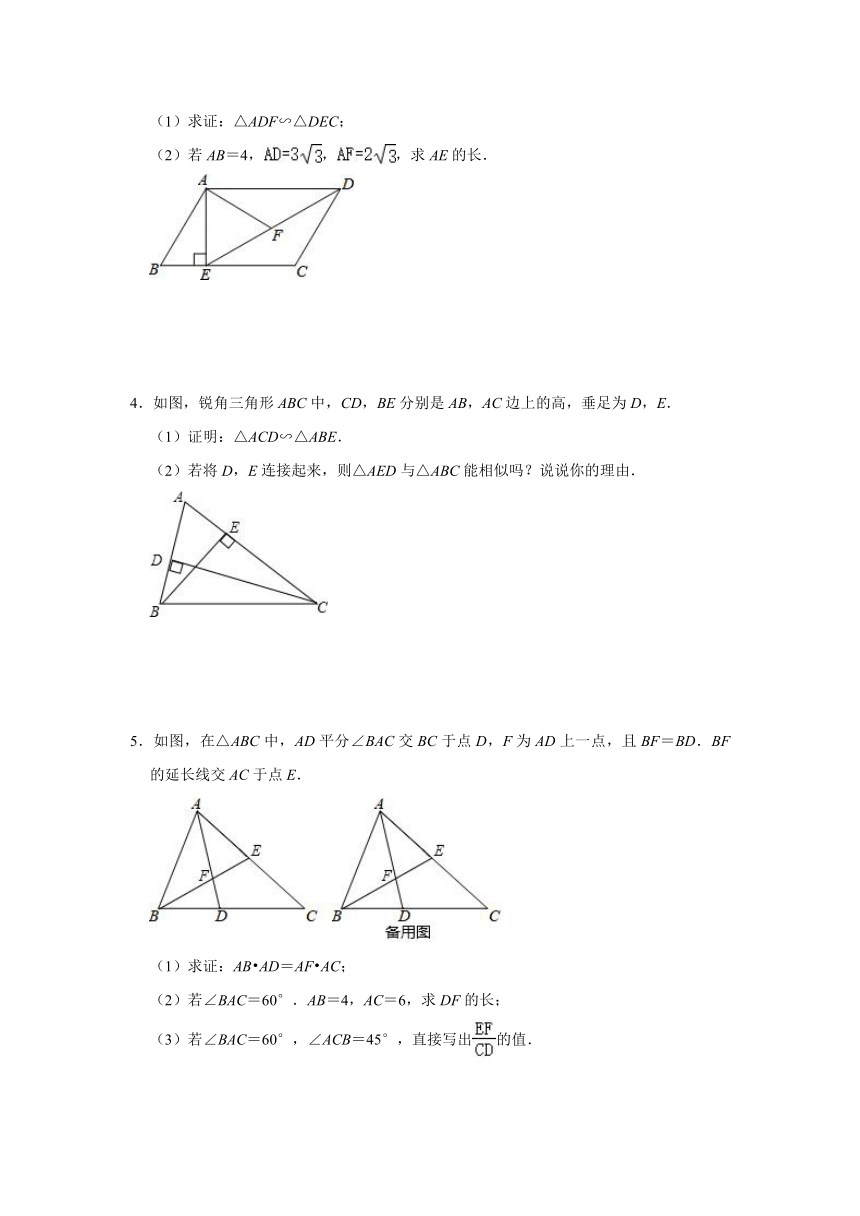
3.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为点E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=4,,,求AE的长.
4.如图,锐角三角形ABC中,CD,BE分别是AB,AC边上的高,垂足为D,E.
(1)证明:△ACD∽△ABE.
(2)若将D,E连接起来,则△AED与△ABC能相似吗?说说你的理由.
5.如图,在△ABC中,AD平分∠BAC交BC于点D,F为AD上一点,且BF=BD.BF的延长线交AC于点E.
(1)求证:AB?AD=AF?AC;
(2)若∠BAC=60°.AB=4,AC=6,求DF的长;
(3)若∠BAC=60°,∠ACB=45°,直接写出的值.
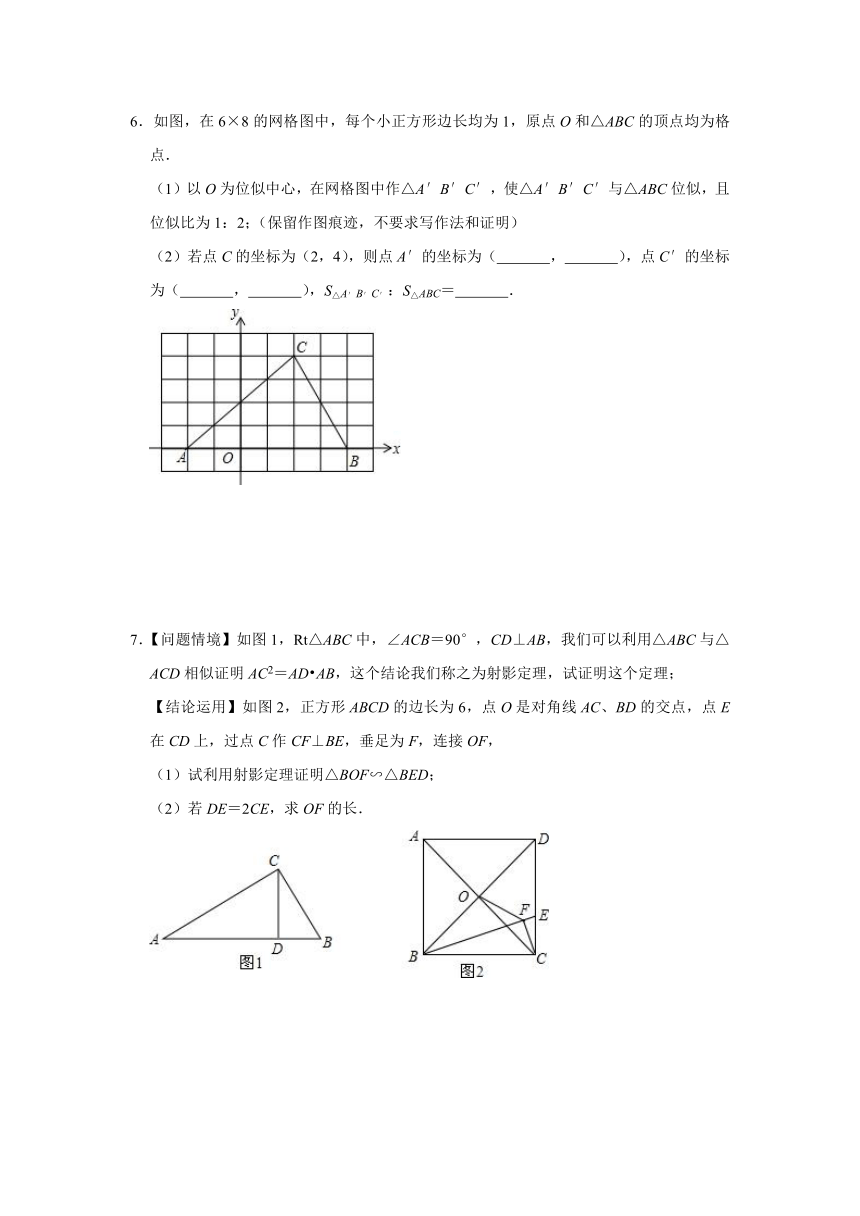
6.如图,在6×8的网格图中,每个小正方形边长均为1,原点O和△ABC的顶点均为格点.
(1)以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′与△ABC位似,且位似比为1:2;(保留作图痕迹,不要求写作法和证明)
(2)若点C的坐标为(2,4),则点A′的坐标为(
,
),点C′的坐标为(
,
),S△A′B′C′:S△ABC=
.
7.【问题情境】如图1,Rt△ABC中,∠ACB=90°,CD⊥AB,我们可以利用△ABC与△ACD相似证明AC2=AD?AB,这个结论我们称之为射影定理,试证明这个定理;
【结论运用】如图2,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,过点C作CF⊥BE,垂足为F,连接OF,
(1)试利用射影定理证明△BOF∽△BED;
(2)若DE=2CE,求OF的长.
8.一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm,把它加工成正方形零件如图1,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)求证:△AEF∽△ABC;
(2)求这个正方形零件的边长;
(3)如果把它加工成矩形零件如图2,问这个矩形的最大面积是多少?
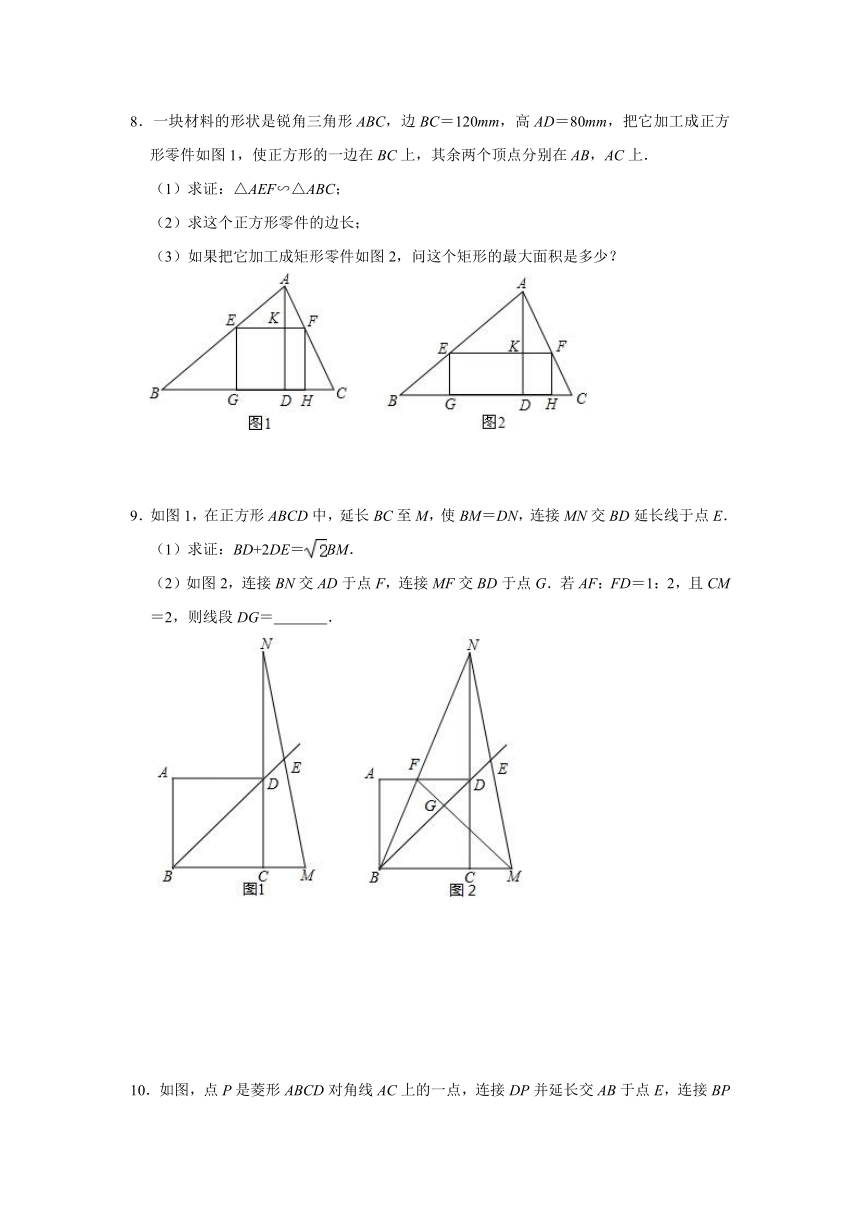
9.如图1,在正方形ABCD中,延长BC至M,使BM=DN,连接MN交BD延长线于点E.
(1)求证:BD+2DE=BM.
(2)如图2,连接BN交AD于点F,连接MF交BD于点G.若AF:FD=1:2,且CM=2,则线段DG=
.
10.如图,点P是菱形ABCD对角线AC上的一点,连接DP并延长交AB于点E,连接BP并延长交AD于点F,交CD延长线于点G.
(1)求证:PB=PD.
(2)若DF:FA=1:2
①请写出线段PF与线段PD之间满足的数量关系,并说明理由;
②当△DGP是等腰三角形时,求tan∠DAB的值.
参考答案
1.解:(1)分别过点D、A作DF⊥BC、AG⊥BC,垂足为F、G
如图
∴DF∥AG,=
∵AB=AC=10,BC=16∴BG=8,∴AG=6.
∵AD=BE=t,∴BD=10﹣t,
∴=
解得DF=(10﹣t)
∵S△BDE=BE?DF=7.5
∴(10﹣t)?t=15
解得t=5.
答:t为5秒时,△BDE的面积为7.5cm2.
(2)存在.理由如下:
①当BE=DE时,△BDE∽△BCA,
∴=即=,
解得t=,
②当BD=DE时,△BDE∽△BAC,
=即=,
解得t=.
答:存在时间t为或秒时,使得△BDE与△ABC相似.
2.解:根据勾股定理得:BA=;
(1)分两种情况讨论:
①当△BPQ∽△BAC时,,
∵BP=5t,QC=4t,AB=10,BC=8,
∴,解得,t=1,
②当△BPQ∽△BCA时,,
∴,解得,t=;
∴t=1或时,△BPQ∽△BCA;
(2)过P作PM⊥BC于点M,AQ,CP交于点N,如图所示:
则PB=5t,PM=3t,MC=8﹣4t,
∵∠NAC+∠NCA=90°,∠PCM+∠NCA=90°,
∴∠NAC=∠PCM,
∵∠ACQ=∠PMC,
∴△ACQ∽△CMP,
∴,
∴,解得t=.
3.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠B+∠C=180°,∠ADF=∠DEC.
∵∠AFD+∠AFE=180°,∠AFE=∠B
∴∠AFD=∠C
∴△ADF∽△DEC;
(2)解:∵四边形ABCD是平行四边形,
∴CD=AB=4,
由(1)知△ADF∽△DEC,
∴,
∴.
在Rt△ADE中,由勾股定理得:.
4.证明:(1)∵CD,BE分别是AB,AC边上的高,
∴∠ADC=∠AEB=90°.
∵∠A=∠A,
∴△ACD∽△ABE.
(2)连接DE,
∵△ACD∽△ABE,
∴AD:AE=AC:AB,
∴AD:AC=AE:AB,
∵∠A=∠A,
∴△AED∽△ABC.
5.解:
(1)∵AD平分∠BAC
∴∠BAF=∠DAC
又∵BF=BD
∴∠BFD=∠FDB
∴∠AFB=∠ADC
∴△AFB∽△ADC
∴.
∴AB?AD=AF?AC
(2)作BH⊥AD于H,作CN⊥AD于N,则BH=AB=2,CN=AC=3
∴AH=BH=2,AN=CN=3
∴HN=
∵∠BDH=∠CDN
∴△BHD∽△CND
∴
∴HD=
又∵BF=BD,BH⊥DF
∴DF=2HD=
(3)由(1)得△AFB∽△ADC,
∴①,易证△ABD,△AEF,△BFD均为顶角为30°的等腰三角形
∴AB=AD,AE=AF,BF=BD
易证△ABD∽△AEF
∴②
∴①×②得==,过F作FG⊥AB于G,设FG=x,则AF=2x,BF=x,AG=x,BG=x
∴AB=(+1)x,
∴==4﹣2
6.解:(1)如图所示:△A′B′C′即为所求;
(2)A′(﹣1,0),
C′(1,2),
S△A′B′C′:S△ABC=1:4.
故答案为:﹣1,0;1,2;1:4.
7.【问题情境】
证明:如图1,
∵CD⊥AB,
∴∠ADC=90°,
而∠CAD=∠BAC,
∴Rt△ACD∽Rt△ABC,
∴AC:AB=AD:AC,
∴AC2=AD?AB;
【结论运用】
(1)证明:如图2,
∵四边形ABCD为正方形,
∴OC⊥BO,∠BCD=90°,
∴BC2=BO?BD,
∵CF⊥BE,
∴BC2=BF?BE,
∴BO?BD=BF?BE,
即=,
而∠OBF=∠EBD,
∴△BOF∽△BED;
(2)∵BC=CD=6,
而DE=2CE,
∴DE=4,CE=2,
在Rt△BCE中,BE==2,
在Rt△OBC中,OB=BC=3,
∵△BOF∽△BED,
∴=,即=,
∴OF=.
8.解:(1)∵四边形EGFH为正方形,
∴BC∥EF,
∴△AEF∽△ABC;
(2)设正方形零件的边长为x
mm,则KD=EF=x,AK=80﹣x,
∵EF∥BC,
∴△AEF∽△ABC,
∵AD⊥BC,
∴,
∴,
解得x=48.
答:正方形零件的边长为48mm.
(3)设EF=x,EG=y,
∵△AEF∽△ABC
∴,
∴=
∴y=80﹣x
∴矩形面积S=xy=﹣x2+80x=﹣(x﹣60)2+2400(0<x<120)
故当x=60时,此时矩形的面积最大,最大面积为2400mm2.
9.(1)证明:过点M作MP⊥BC交BD的延长线于点P,
∵四边形ABCD是正方形,
∴∠BCD=90°,∠DBC=∠BDC=45°,
∴PM∥CN,
∴∠N=∠EMP,∠BDC=∠MPB=45°,
∴BM=PM,
∵BM=DN,
∴DN=MP,
在△DEN和△PEM中
,
∴△DEN≌△PEM,
∴DE=EP,
∵△BMP是等腰直角三角形
∴BP=BM
∴BD+2DE=BM.
(2)解:∵AF:FD=1:2,
∴DF:BC=2:3,
∵△BCN∽△FDN,
∴
设正方形边长为a,又知CM=2,
∴BM=DN=a+2,CN=2a+2
∴,
解得:a=2,
∴DF=,BM=4,BD=2,
又∵△DFG∽△BMG,
∴,
∴,
∴DG=.
故答案为:.
10.(1)证明:∵四边形ABCD是菱形,
∴AB=AD,AC平分∠DAB,
∴∠DAP=∠BAP,
在△APB和△APD中,
,
∴△APB≌△APD,
∴PB=PD;
(2)解:①∵四边形ABCD是菱形,
∴AD∥BC,AD=BC,
∴△AFP∽△CBP,
∴,
∵,
∴,
∴,
由(1)知PB=PD,
∴,
∴PF=PD.
②由(1)证得△APB≌△APD,
∴∠ABP=∠ADP,
∵GC∥AB,
∴∠G=∠ABP,
∴∠ADP=∠G,
∴∠GDP>∠G,
∴PD≠PG.
(Ⅰ),若DG=PG,
∵DG∥AB,
∴△DGP∽△EBP,
∴PB=EB,
由(2)知,设PF=2a,
则PB=BE=PD=3a,PE=PF=2a,BF=5a,
由△DGP∽△EBP,得DG=a,
∴AB=AD=2DG=9a,
∴AF=6a,
如图1,作FH⊥AB于H,设AH=x,
则(6a)2﹣x2=(5a)2﹣(9a﹣x)2,
解得x=a,∴FH=,
∴tan∠DAB=;
(Ⅱ)若DG=DP,如图2,
设DG=DP=3m,则PB=3m,PE=BE=PF=2m,
AB=AD=2DG=6m,AF=4m,BF=5m,
设AH=x,
∴(4m)2﹣x2=(5m)2﹣(6m﹣x)2,
解得x=m,
∴FH=,
∴tan∠DAB==.
1.如图所示,在等腰△ABC中,AB=AC=10cm,BC=16cm.点D由点A出发沿AB方向向点B匀速运动,同时点E由点B出发沿BC方向向点C匀速运动,它们的速度均为1cm/s.连接DE,设运动时间为t(s)(0<t<10),解答下列问题:
(1)当t为何值时,△BDE的面积为7.5cm2;
(2)在点D,E的运动中,是否存在时间t,使得△BDE与△ABC相似?若存在,请求出对应的时间t;若不存在,请说明理由.
2.如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)连接AQ、CP,若AQ⊥CP,求t的值.
3.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为点E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=4,,,求AE的长.
4.如图,锐角三角形ABC中,CD,BE分别是AB,AC边上的高,垂足为D,E.
(1)证明:△ACD∽△ABE.
(2)若将D,E连接起来,则△AED与△ABC能相似吗?说说你的理由.
5.如图,在△ABC中,AD平分∠BAC交BC于点D,F为AD上一点,且BF=BD.BF的延长线交AC于点E.
(1)求证:AB?AD=AF?AC;
(2)若∠BAC=60°.AB=4,AC=6,求DF的长;
(3)若∠BAC=60°,∠ACB=45°,直接写出的值.
6.如图,在6×8的网格图中,每个小正方形边长均为1,原点O和△ABC的顶点均为格点.
(1)以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′与△ABC位似,且位似比为1:2;(保留作图痕迹,不要求写作法和证明)
(2)若点C的坐标为(2,4),则点A′的坐标为(
,
),点C′的坐标为(
,
),S△A′B′C′:S△ABC=
.
7.【问题情境】如图1,Rt△ABC中,∠ACB=90°,CD⊥AB,我们可以利用△ABC与△ACD相似证明AC2=AD?AB,这个结论我们称之为射影定理,试证明这个定理;
【结论运用】如图2,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,过点C作CF⊥BE,垂足为F,连接OF,
(1)试利用射影定理证明△BOF∽△BED;
(2)若DE=2CE,求OF的长.
8.一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm,把它加工成正方形零件如图1,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)求证:△AEF∽△ABC;
(2)求这个正方形零件的边长;
(3)如果把它加工成矩形零件如图2,问这个矩形的最大面积是多少?
9.如图1,在正方形ABCD中,延长BC至M,使BM=DN,连接MN交BD延长线于点E.
(1)求证:BD+2DE=BM.
(2)如图2,连接BN交AD于点F,连接MF交BD于点G.若AF:FD=1:2,且CM=2,则线段DG=
.
10.如图,点P是菱形ABCD对角线AC上的一点,连接DP并延长交AB于点E,连接BP并延长交AD于点F,交CD延长线于点G.
(1)求证:PB=PD.
(2)若DF:FA=1:2
①请写出线段PF与线段PD之间满足的数量关系,并说明理由;
②当△DGP是等腰三角形时,求tan∠DAB的值.
参考答案
1.解:(1)分别过点D、A作DF⊥BC、AG⊥BC,垂足为F、G
如图
∴DF∥AG,=
∵AB=AC=10,BC=16∴BG=8,∴AG=6.
∵AD=BE=t,∴BD=10﹣t,
∴=
解得DF=(10﹣t)
∵S△BDE=BE?DF=7.5
∴(10﹣t)?t=15
解得t=5.
答:t为5秒时,△BDE的面积为7.5cm2.
(2)存在.理由如下:
①当BE=DE时,△BDE∽△BCA,
∴=即=,
解得t=,
②当BD=DE时,△BDE∽△BAC,
=即=,
解得t=.
答:存在时间t为或秒时,使得△BDE与△ABC相似.
2.解:根据勾股定理得:BA=;
(1)分两种情况讨论:
①当△BPQ∽△BAC时,,
∵BP=5t,QC=4t,AB=10,BC=8,
∴,解得,t=1,
②当△BPQ∽△BCA时,,
∴,解得,t=;
∴t=1或时,△BPQ∽△BCA;
(2)过P作PM⊥BC于点M,AQ,CP交于点N,如图所示:
则PB=5t,PM=3t,MC=8﹣4t,
∵∠NAC+∠NCA=90°,∠PCM+∠NCA=90°,
∴∠NAC=∠PCM,
∵∠ACQ=∠PMC,
∴△ACQ∽△CMP,
∴,
∴,解得t=.
3.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠B+∠C=180°,∠ADF=∠DEC.
∵∠AFD+∠AFE=180°,∠AFE=∠B
∴∠AFD=∠C
∴△ADF∽△DEC;
(2)解:∵四边形ABCD是平行四边形,
∴CD=AB=4,
由(1)知△ADF∽△DEC,
∴,
∴.
在Rt△ADE中,由勾股定理得:.
4.证明:(1)∵CD,BE分别是AB,AC边上的高,
∴∠ADC=∠AEB=90°.
∵∠A=∠A,
∴△ACD∽△ABE.
(2)连接DE,
∵△ACD∽△ABE,
∴AD:AE=AC:AB,
∴AD:AC=AE:AB,
∵∠A=∠A,
∴△AED∽△ABC.
5.解:
(1)∵AD平分∠BAC
∴∠BAF=∠DAC
又∵BF=BD
∴∠BFD=∠FDB
∴∠AFB=∠ADC
∴△AFB∽△ADC
∴.
∴AB?AD=AF?AC
(2)作BH⊥AD于H,作CN⊥AD于N,则BH=AB=2,CN=AC=3
∴AH=BH=2,AN=CN=3
∴HN=
∵∠BDH=∠CDN
∴△BHD∽△CND
∴
∴HD=
又∵BF=BD,BH⊥DF
∴DF=2HD=
(3)由(1)得△AFB∽△ADC,
∴①,易证△ABD,△AEF,△BFD均为顶角为30°的等腰三角形
∴AB=AD,AE=AF,BF=BD
易证△ABD∽△AEF
∴②
∴①×②得==,过F作FG⊥AB于G,设FG=x,则AF=2x,BF=x,AG=x,BG=x
∴AB=(+1)x,
∴==4﹣2
6.解:(1)如图所示:△A′B′C′即为所求;
(2)A′(﹣1,0),
C′(1,2),
S△A′B′C′:S△ABC=1:4.
故答案为:﹣1,0;1,2;1:4.
7.【问题情境】
证明:如图1,
∵CD⊥AB,
∴∠ADC=90°,
而∠CAD=∠BAC,
∴Rt△ACD∽Rt△ABC,
∴AC:AB=AD:AC,
∴AC2=AD?AB;
【结论运用】
(1)证明:如图2,
∵四边形ABCD为正方形,
∴OC⊥BO,∠BCD=90°,
∴BC2=BO?BD,
∵CF⊥BE,
∴BC2=BF?BE,
∴BO?BD=BF?BE,
即=,
而∠OBF=∠EBD,
∴△BOF∽△BED;
(2)∵BC=CD=6,
而DE=2CE,
∴DE=4,CE=2,
在Rt△BCE中,BE==2,
在Rt△OBC中,OB=BC=3,
∵△BOF∽△BED,
∴=,即=,
∴OF=.
8.解:(1)∵四边形EGFH为正方形,
∴BC∥EF,
∴△AEF∽△ABC;
(2)设正方形零件的边长为x
mm,则KD=EF=x,AK=80﹣x,
∵EF∥BC,
∴△AEF∽△ABC,
∵AD⊥BC,
∴,
∴,
解得x=48.
答:正方形零件的边长为48mm.
(3)设EF=x,EG=y,
∵△AEF∽△ABC
∴,
∴=
∴y=80﹣x
∴矩形面积S=xy=﹣x2+80x=﹣(x﹣60)2+2400(0<x<120)
故当x=60时,此时矩形的面积最大,最大面积为2400mm2.
9.(1)证明:过点M作MP⊥BC交BD的延长线于点P,
∵四边形ABCD是正方形,
∴∠BCD=90°,∠DBC=∠BDC=45°,
∴PM∥CN,
∴∠N=∠EMP,∠BDC=∠MPB=45°,
∴BM=PM,
∵BM=DN,
∴DN=MP,
在△DEN和△PEM中
,
∴△DEN≌△PEM,
∴DE=EP,
∵△BMP是等腰直角三角形
∴BP=BM
∴BD+2DE=BM.
(2)解:∵AF:FD=1:2,
∴DF:BC=2:3,
∵△BCN∽△FDN,
∴
设正方形边长为a,又知CM=2,
∴BM=DN=a+2,CN=2a+2
∴,
解得:a=2,
∴DF=,BM=4,BD=2,
又∵△DFG∽△BMG,
∴,
∴,
∴DG=.
故答案为:.
10.(1)证明:∵四边形ABCD是菱形,
∴AB=AD,AC平分∠DAB,
∴∠DAP=∠BAP,
在△APB和△APD中,
,
∴△APB≌△APD,
∴PB=PD;
(2)解:①∵四边形ABCD是菱形,
∴AD∥BC,AD=BC,
∴△AFP∽△CBP,
∴,
∵,
∴,
∴,
由(1)知PB=PD,
∴,
∴PF=PD.
②由(1)证得△APB≌△APD,
∴∠ABP=∠ADP,
∵GC∥AB,
∴∠G=∠ABP,
∴∠ADP=∠G,
∴∠GDP>∠G,
∴PD≠PG.
(Ⅰ),若DG=PG,
∵DG∥AB,
∴△DGP∽△EBP,
∴PB=EB,
由(2)知,设PF=2a,
则PB=BE=PD=3a,PE=PF=2a,BF=5a,
由△DGP∽△EBP,得DG=a,
∴AB=AD=2DG=9a,
∴AF=6a,
如图1,作FH⊥AB于H,设AH=x,
则(6a)2﹣x2=(5a)2﹣(9a﹣x)2,
解得x=a,∴FH=,
∴tan∠DAB=;
(Ⅱ)若DG=DP,如图2,
设DG=DP=3m,则PB=3m,PE=BE=PF=2m,
AB=AD=2DG=6m,AF=4m,BF=5m,
设AH=x,
∴(4m)2﹣x2=(5m)2﹣(6m﹣x)2,
解得x=m,
∴FH=,
∴tan∠DAB==.
