内蒙古赤峰市第二高级中学2021届高三下学期第一次月考数学(文)试题 Word版含答案
文档属性
| 名称 | 内蒙古赤峰市第二高级中学2021届高三下学期第一次月考数学(文)试题 Word版含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 967.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-22 00:00:00 | ||
图片预览



文档简介
赤峰二中2021届高三下学期第一次月考
文科数学
一、选择题
1.已知集合false,集合false,则false( )
A.false B.false C.false D.false
2.若复数false满足false (其中false为虚数单位)则复数false的虚部为( )
A.false B.false C.false D.false
3.良渚遗址是人类早期城市文明的范例,是华夏五千年文明史的实证之一,2019年获准列入世界遗产名录.考古学家在测定遗址年代的过程中,利用“生物死亡后体内的碳14含量按确
定的比率衰减”这一规律,建立了样本中碳14的含量y随时间x(年)变化的数学模型:false(false表示碳14的初始量).2020年考古学家对良渚遗址某文物样本进行碳14年代学检测,检测出碳14的含量约为初始量的55%,据此推测良渚遗址存在的时期距今大约是(参考数据:false,false)( )
A.3450年 B.4010年 C.4580年 D.5160年
4.已知非零向量false、false满足false,且false,则false与false的夹角为( )
A.false B.false C.false D.false
5.已知平面false平面false,false,false,则下列结论一定正确的是( )
A.false,false是平行直线 B.false,false是异面直线
C.false,false是共面直线 D.false,false是不相交直线
6.在false中,角false,false,false所对的边分别为false,false,false,若false,则false的形状为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不确定
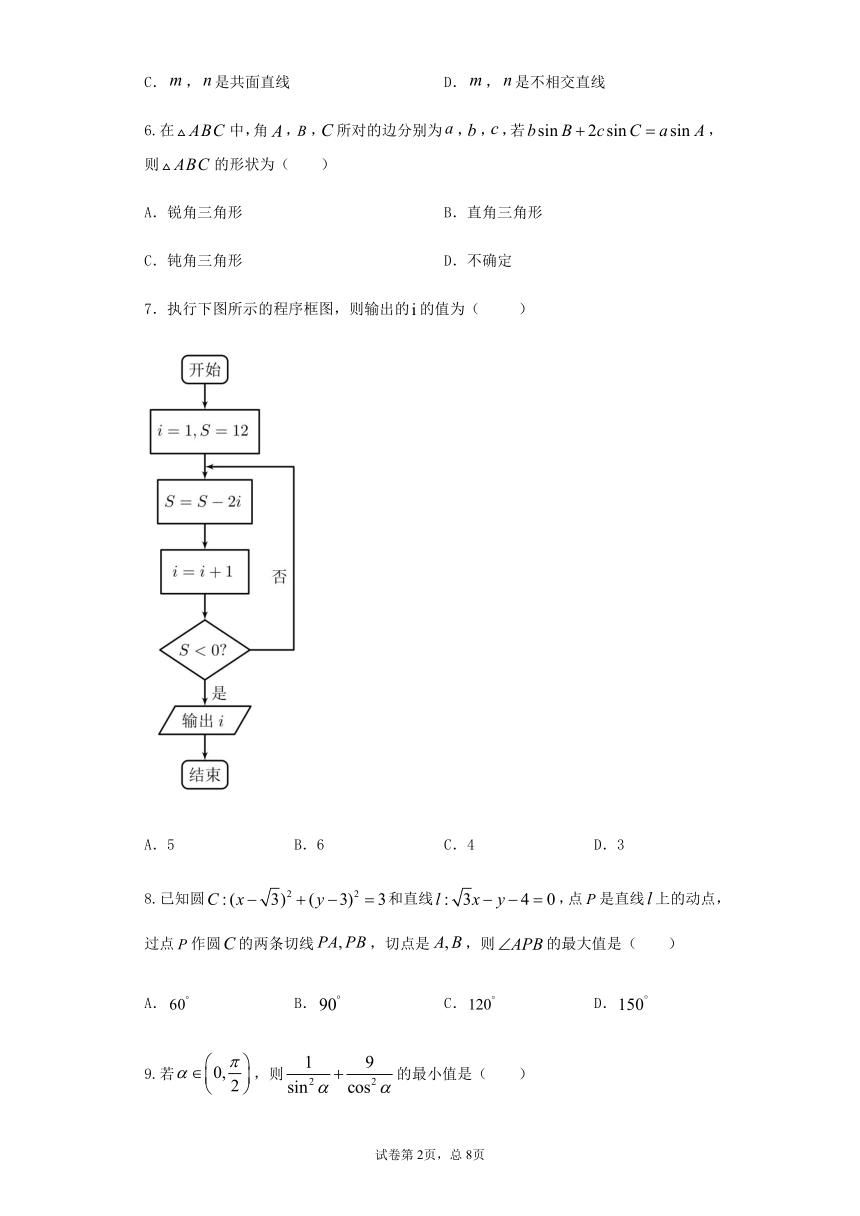
7.执行下图所示的程序框图,则输出的false的值为( )
A.5 B.6 C.4 D.3
8.已知圆false和直线false,点false是直线false上的动点,过点false作圆false的两条切线false,切点是false,则false的最大值是( )
A.false B.false C.false D.false
9.若false,则false的最小值是( )
A.false B.false C.false D.false
10.意大利著名天文学家伽利略曾错误地猜测链条自然下垂时的形状是抛物线.直到1690年,雅各布·伯努利正式提出该问题为“悬链线”问题并向数学界征求答案.1691年他的弟弟约翰·伯努利和菜布尼兹?惠更斯三人各自都得到了正确答案,给出悬链线的数学表达式——双曲余弦函数:falsefalse(false为自然对数的底数).当false,false时,记false,false,false,则false,false,false的大小关系为( )
A.false B.false
C.false D.false
11.已知抛物线false的焦点为false,准线为false,点false分别在抛物线false上,且false,直线false交false于点false,false,垂足为false,若false的面积为false,则false到false的距离为()
A.false B.false C.8 D.6
12.设实数false,已知函数f(x)=false,若函数false在区间false上有两个零点false,则false的取值范围是( )
A.false B.false
C.false D.false
二、填空题
13.已知变量false,false满足约束条件false则false的最大值为____ .
14.甲、乙两个学习小组各有五名同学,如图是甲、乙两组同学某次数学月考成绩(单位:分)的茎叶图,已知在这次数学月考中,甲组成绩的中位数为false,乙组成绩的平均数为false,则false的值为____ ___
15.已知false为偶函数,若曲线false在点false处的切线方程为false,则false___ ____.
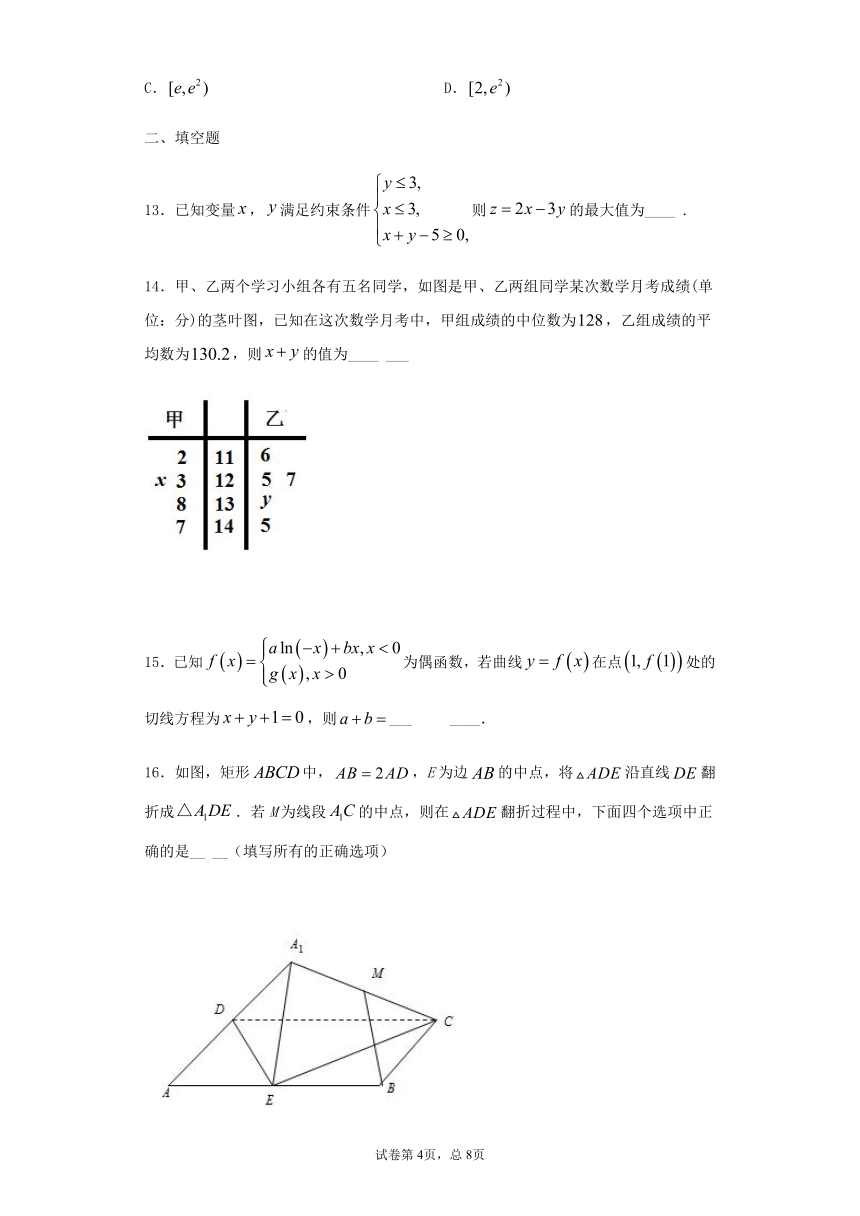
16.如图,矩形false中,false,E为边false的中点,将false沿直线false翻折成false.若M为线段false的中点,则在false翻折过程中,下面四个选项中正确的是__ __(填写所有的正确选项)
(1)false是定值
(2)点M在某个球面上运动
(3)存在某个位置,使false
(4)存在某个位置,使false平面false
三、解答题
17.从下列①②③选项中,选择其中一个作为条件进行解答:
①已知数列false的前n项和false;
②已知数列false是等比数列,false,false;
③已知数列false中,false,且对任意的正整数m,n都有false.
(1)求数列false的通项公式;
(2)已知false,求数列false的前2021项的和false.
18.如图,在四棱锥false中,false平面ABCD.false,false,false,E是PD的中点.
(1)证明:false平面PBC;
(2)若false,求三棱锥false的体积.
19.自从新型冠状病毒爆发以来,美国疫情持续升级,以下是美国2020年4月9日-12月14日每隔25天统计1次共11次累计确诊人数(万).
日期(月/日)
4/09
5/04
5/29
6/23
7/18
8/13
9/06
10/01
10/26
11/19
12/14
统计时间顺序false
1
2
3
4
5
6
7
8
9
10
11
累计确诊人数false
43.3
118.8
179.4
238.8
377.0
536.0
646.0
744.7
888.9
1187.4
1673.7
(1)将4月9日作为第1次统计,若将统计时间顺序作为变量false,每次累计确诊人数作为变量false,得到函数关系false(false?false).对上表的数据作初步处理,得到部分数据已作近似处理的一些统计量的值false,false,false,false,false,false,false,false,false,false.根据相关数据,确定该函数关系式(函数的参数精确到0.01).
(2)为了了解患新冠肺炎与年龄的关系,已知某地患有新冠肺炎的老年、中年、青年的人数分别为45人,30人,15人,按分层抽样的方法随机抽取6人进行问卷调查,再从6人中随机抽取2人进行调查结果对比,求这2人中至少一人是老年人的概率.
附参考公式:回归直线false的斜率和截距的最小二乘估计分别为
false,false
20.已知椭圆false的离心率为false,短轴长为false.
(1)求椭圆C的方程;
(2)设A,B分别为椭圆C的左、右顶点,若过点false且斜率不为0的直线l与椭圆C交于M、N两点,直线AM与BN相交于点Q.证明:点Q在定直线上.
21.已知函数false.
(1)当false时,求函数false的单调区间;
(2)若false(false为自然对数的底数),不等式false恒成立,求false的取值范围.
22.在极坐标系中,曲线C的极坐标方程为false,点P的极坐标为false,以极点为坐标原点,极轴为x轴正半轴,建立平面直角坐标系.
(1)求曲线C的直角坐标方程和点P的直角坐标;
(2)已知直线false(t为参数),若直线l与曲线C的交点分别是A、B,求falsefalse的值.
23.设函数false.
(1)解不等式false;
(2)若关于x的方程false没有实数根,求实数m的取值范围.
参考答案
1-12 C A C B D C A C A C D D
13.0
14.16
15.3
16.124
17.(1)条件选择见解析;false;(2)false.
【分析】
(1)选①:利用公式false进行求解即可.
选②:利用等比数列的通项公式进行求解即可.
选③:通过取特殊值,结合等比数列的定义进行求解即可;
(2)根据对数的运算性质,结合裂项相消法进行求解即可.
【详解】
(1)若选①,当false时,false,
当false时,false,显然当false时,false也适合,
所以false.
若选②,设等比数列false的公比为false,
因为false,false,所以有false,
解得false,false,false.
若选③,令false,falsefalse是以false为首项,公比为false的等比数列,
因此false;
(2)由题意知,false,
false.
18.(1)证明见解析;(2)false.
【分析】
(1)取PC的中点F,连接EF、BF,可证明四边形false是平行四边形,根据线面平行的判定定理,即可得证;
(2)根据题中条件及余弦定理,可求得AC的长,根据勾股定理,可证false,根据E为PD中点,可得false,代入数据,计算整理,即可得结果.
【详解】
(1)证明:取PC的中点F,连接EF、BF,如图所示:
因为E、F分别为PD,PC的中点,
所以false且false,
又false,false,
所以false且false
所以四边形false是平行四边形,
所以false,
又因为false平面PBC,false平面PBC
所以false平面PBC.
(2)因为AB=1,false,false,
所以false,即false,
所以false,即false,
因为E是PD的中点,
所以false,
又false,所以false,所以false,
所以false,
所以false.
【点睛】
解题的关键是利用等体积法,false,进行转换,可大大简化计算,提高正确率,属基础题.
19.【详解】
(1)false两边同时取对,得false,
false,false,得false.
所以函数关系式为false.
(2)由题意抽取的false人中,老年人有false人,设老年人为false,其他人是false,所以所有的基本事件为
false,
false
基本事件总数为false个,这false人中至少一人是老年人有false个,所以概率为false.
20.(1)false;(2)证明见解析.
【分析】
(1)用离心率公式和false列方程求得false,即可得椭圆方程;
(2)方法一:设直线false,false,false联立椭圆方程,由韦达定理得false关系,由直线false和false方程联立求解交点坐标,并化简得false,即可证明问题;
方法二:设false,false,false,false两两不等,
因为P,M,N三点共线,由斜率相等得到方程,同理A,M,Q三点共线与B,N,Q三点共线也得到两方程,再结合三条方程求解false,即可证明问题.
【详解】
解:(1)因为椭圆的离心率false,false,false,
又false,false.
因为false,所以false,false,
所以椭圆C的方程为false.
(2)解法一:设直线false,false,false,
false,可得false,
所以false.
直线AM的方程:false①
直线BN的方程:false②
由对称性可知:点Q在垂直于x轴的直线上,
联立①②可得false.
因为false,
所以false
所以点Q在直线false上.
解法二:设false,false,false,false两两不等,
因为P,M,N三点共线,
所以false,
整理得:false.
又A,M,Q三点共线,有:false①
又B,N,Q三点共线,有false②将①与②两式相除得:
false
false
即false,
将false即false
代入得:false解得false(舍去)或false,(因为直线false与椭圆相交故false)
所以Q在定直线false上.
【点晴】
求解直线与圆锥曲线定点定值问题:关键在于运用设而不求思想、联立方程和韦达定理,构造坐标点方程从而解决相关问题.
21.(1)单调递减区间是false,单调递增区间是false;(2)false.
【分析】
(1)当false时,求false的导数,分析导函数的正负求单调区间.
(2)若false,不等式false恒成立
将其转化为求false在false上的最小值false,分类讨论可得false的取值范围.
【详解】
解:(1)由题意知false的定义域是false
因为false,
令false得false(舍),
false由false得false
所以false的单调递减区间是false,单调递增区间是false
(2)因为false,false恒成立,
有false,false,
即false在false上恒成立,
所以false在false上的最小值false.
由(1)知:
① 当false,即false时,false在false上单调递减,
false,
即false,false,false,
② 当false,即false时,false在false上单调递增,
false,即false
③ 当false,即false时,
false在false上单调递减,在false上单调递增,
因为false,false,
从而false,此时false成立,
综上:a的取值范围为false.
【点睛】
用导数求函数的单调区间或判断函数的单调性问题时应注意如下几方面:
(1)在利用导数讨论函数的单调区间时,首先要确定函数的定义域;
(2)不能随意将函数的2个独立的单调递增(或递减)区间写成并集形式;
(3)利用导数解决含参函数的单调性问题时,一般将其转化为不等式恒成立问题,解题过程中要注意分类讨论和数形结合思想的应用.
22.(1)false;false;(2)4.
【分析】
(1)false两边同时乘以false,由false,false可得直角坐标方程以及点P的直角坐标.
(2)将直线的参数方程代入C方程,利用参数false的几何意义即可求解.
【详解】
解:(1)由false,得false,
又false,false,∴false,
即曲线C的直角坐标方程为false,
点P的直角坐标为false.
(2)把直线l的方程代入C方程,整理得false,
false,
设A、B对应的参数分别是false、false,则false,
于是false
23.(1)false;(2)false.
【分析】
(1)分段讨论去绝对值解不等式即可;
(2)先将题意转化为false没有实数根, 再求false值域,利用false取值为false值域的补集,计算即得结果.
【详解】
解:(1)当false时,false,
得false,所以false;
当false时,false,
得false,所以false;
当false时,false,得false,所以false.
综上,原不等式的解集为false;
(2)方程false没有实数根,即false没有实数根,
令false,
当且仅当false时,即false时等号成立,即false值域为false,
若false没有实数根,则false,即false,
所以实数m的取值范围为false.
【点睛】
方法点睛:
1、绝对值不等式的解法:
(1)利用绝对值不等式的几何意义求解,体现了数形结合的思想;
(2)利于“零点分段法”去绝对值进行求解,体现了分类讨论思想;
(3)通过构造函数,利用函数图象求解,体现了函数与方程思想.
2、不等式恒成立问题通常可转化成函数最值来处理.
文科数学
一、选择题
1.已知集合false,集合false,则false( )
A.false B.false C.false D.false
2.若复数false满足false (其中false为虚数单位)则复数false的虚部为( )
A.false B.false C.false D.false
3.良渚遗址是人类早期城市文明的范例,是华夏五千年文明史的实证之一,2019年获准列入世界遗产名录.考古学家在测定遗址年代的过程中,利用“生物死亡后体内的碳14含量按确
定的比率衰减”这一规律,建立了样本中碳14的含量y随时间x(年)变化的数学模型:false(false表示碳14的初始量).2020年考古学家对良渚遗址某文物样本进行碳14年代学检测,检测出碳14的含量约为初始量的55%,据此推测良渚遗址存在的时期距今大约是(参考数据:false,false)( )
A.3450年 B.4010年 C.4580年 D.5160年
4.已知非零向量false、false满足false,且false,则false与false的夹角为( )
A.false B.false C.false D.false
5.已知平面false平面false,false,false,则下列结论一定正确的是( )
A.false,false是平行直线 B.false,false是异面直线
C.false,false是共面直线 D.false,false是不相交直线
6.在false中,角false,false,false所对的边分别为false,false,false,若false,则false的形状为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不确定
7.执行下图所示的程序框图,则输出的false的值为( )
A.5 B.6 C.4 D.3
8.已知圆false和直线false,点false是直线false上的动点,过点false作圆false的两条切线false,切点是false,则false的最大值是( )
A.false B.false C.false D.false
9.若false,则false的最小值是( )
A.false B.false C.false D.false
10.意大利著名天文学家伽利略曾错误地猜测链条自然下垂时的形状是抛物线.直到1690年,雅各布·伯努利正式提出该问题为“悬链线”问题并向数学界征求答案.1691年他的弟弟约翰·伯努利和菜布尼兹?惠更斯三人各自都得到了正确答案,给出悬链线的数学表达式——双曲余弦函数:falsefalse(false为自然对数的底数).当false,false时,记false,false,false,则false,false,false的大小关系为( )
A.false B.false
C.false D.false
11.已知抛物线false的焦点为false,准线为false,点false分别在抛物线false上,且false,直线false交false于点false,false,垂足为false,若false的面积为false,则false到false的距离为()
A.false B.false C.8 D.6
12.设实数false,已知函数f(x)=false,若函数false在区间false上有两个零点false,则false的取值范围是( )
A.false B.false
C.false D.false
二、填空题
13.已知变量false,false满足约束条件false则false的最大值为____ .
14.甲、乙两个学习小组各有五名同学,如图是甲、乙两组同学某次数学月考成绩(单位:分)的茎叶图,已知在这次数学月考中,甲组成绩的中位数为false,乙组成绩的平均数为false,则false的值为____ ___
15.已知false为偶函数,若曲线false在点false处的切线方程为false,则false___ ____.
16.如图,矩形false中,false,E为边false的中点,将false沿直线false翻折成false.若M为线段false的中点,则在false翻折过程中,下面四个选项中正确的是__ __(填写所有的正确选项)
(1)false是定值
(2)点M在某个球面上运动
(3)存在某个位置,使false
(4)存在某个位置,使false平面false
三、解答题
17.从下列①②③选项中,选择其中一个作为条件进行解答:
①已知数列false的前n项和false;
②已知数列false是等比数列,false,false;
③已知数列false中,false,且对任意的正整数m,n都有false.
(1)求数列false的通项公式;
(2)已知false,求数列false的前2021项的和false.
18.如图,在四棱锥false中,false平面ABCD.false,false,false,E是PD的中点.
(1)证明:false平面PBC;
(2)若false,求三棱锥false的体积.
19.自从新型冠状病毒爆发以来,美国疫情持续升级,以下是美国2020年4月9日-12月14日每隔25天统计1次共11次累计确诊人数(万).
日期(月/日)
4/09
5/04
5/29
6/23
7/18
8/13
9/06
10/01
10/26
11/19
12/14
统计时间顺序false
1
2
3
4
5
6
7
8
9
10
11
累计确诊人数false
43.3
118.8
179.4
238.8
377.0
536.0
646.0
744.7
888.9
1187.4
1673.7
(1)将4月9日作为第1次统计,若将统计时间顺序作为变量false,每次累计确诊人数作为变量false,得到函数关系false(false?false).对上表的数据作初步处理,得到部分数据已作近似处理的一些统计量的值false,false,false,false,false,false,false,false,false,false.根据相关数据,确定该函数关系式(函数的参数精确到0.01).
(2)为了了解患新冠肺炎与年龄的关系,已知某地患有新冠肺炎的老年、中年、青年的人数分别为45人,30人,15人,按分层抽样的方法随机抽取6人进行问卷调查,再从6人中随机抽取2人进行调查结果对比,求这2人中至少一人是老年人的概率.
附参考公式:回归直线false的斜率和截距的最小二乘估计分别为
false,false
20.已知椭圆false的离心率为false,短轴长为false.
(1)求椭圆C的方程;
(2)设A,B分别为椭圆C的左、右顶点,若过点false且斜率不为0的直线l与椭圆C交于M、N两点,直线AM与BN相交于点Q.证明:点Q在定直线上.
21.已知函数false.
(1)当false时,求函数false的单调区间;
(2)若false(false为自然对数的底数),不等式false恒成立,求false的取值范围.
22.在极坐标系中,曲线C的极坐标方程为false,点P的极坐标为false,以极点为坐标原点,极轴为x轴正半轴,建立平面直角坐标系.
(1)求曲线C的直角坐标方程和点P的直角坐标;
(2)已知直线false(t为参数),若直线l与曲线C的交点分别是A、B,求falsefalse的值.
23.设函数false.
(1)解不等式false;
(2)若关于x的方程false没有实数根,求实数m的取值范围.
参考答案
1-12 C A C B D C A C A C D D
13.0
14.16
15.3
16.124
17.(1)条件选择见解析;false;(2)false.
【分析】
(1)选①:利用公式false进行求解即可.
选②:利用等比数列的通项公式进行求解即可.
选③:通过取特殊值,结合等比数列的定义进行求解即可;
(2)根据对数的运算性质,结合裂项相消法进行求解即可.
【详解】
(1)若选①,当false时,false,
当false时,false,显然当false时,false也适合,
所以false.
若选②,设等比数列false的公比为false,
因为false,false,所以有false,
解得false,false,false.
若选③,令false,falsefalse是以false为首项,公比为false的等比数列,
因此false;
(2)由题意知,false,
false.
18.(1)证明见解析;(2)false.
【分析】
(1)取PC的中点F,连接EF、BF,可证明四边形false是平行四边形,根据线面平行的判定定理,即可得证;
(2)根据题中条件及余弦定理,可求得AC的长,根据勾股定理,可证false,根据E为PD中点,可得false,代入数据,计算整理,即可得结果.
【详解】
(1)证明:取PC的中点F,连接EF、BF,如图所示:
因为E、F分别为PD,PC的中点,
所以false且false,
又false,false,
所以false且false
所以四边形false是平行四边形,
所以false,
又因为false平面PBC,false平面PBC
所以false平面PBC.
(2)因为AB=1,false,false,
所以false,即false,
所以false,即false,
因为E是PD的中点,
所以false,
又false,所以false,所以false,
所以false,
所以false.
【点睛】
解题的关键是利用等体积法,false,进行转换,可大大简化计算,提高正确率,属基础题.
19.【详解】
(1)false两边同时取对,得false,
false,false,得false.
所以函数关系式为false.
(2)由题意抽取的false人中,老年人有false人,设老年人为false,其他人是false,所以所有的基本事件为
false,
false
基本事件总数为false个,这false人中至少一人是老年人有false个,所以概率为false.
20.(1)false;(2)证明见解析.
【分析】
(1)用离心率公式和false列方程求得false,即可得椭圆方程;
(2)方法一:设直线false,false,false联立椭圆方程,由韦达定理得false关系,由直线false和false方程联立求解交点坐标,并化简得false,即可证明问题;
方法二:设false,false,false,false两两不等,
因为P,M,N三点共线,由斜率相等得到方程,同理A,M,Q三点共线与B,N,Q三点共线也得到两方程,再结合三条方程求解false,即可证明问题.
【详解】
解:(1)因为椭圆的离心率false,false,false,
又false,false.
因为false,所以false,false,
所以椭圆C的方程为false.
(2)解法一:设直线false,false,false,
false,可得false,
所以false.
直线AM的方程:false①
直线BN的方程:false②
由对称性可知:点Q在垂直于x轴的直线上,
联立①②可得false.
因为false,
所以false
所以点Q在直线false上.
解法二:设false,false,false,false两两不等,
因为P,M,N三点共线,
所以false,
整理得:false.
又A,M,Q三点共线,有:false①
又B,N,Q三点共线,有false②将①与②两式相除得:
false
false
即false,
将false即false
代入得:false解得false(舍去)或false,(因为直线false与椭圆相交故false)
所以Q在定直线false上.
【点晴】
求解直线与圆锥曲线定点定值问题:关键在于运用设而不求思想、联立方程和韦达定理,构造坐标点方程从而解决相关问题.
21.(1)单调递减区间是false,单调递增区间是false;(2)false.
【分析】
(1)当false时,求false的导数,分析导函数的正负求单调区间.
(2)若false,不等式false恒成立
将其转化为求false在false上的最小值false,分类讨论可得false的取值范围.
【详解】
解:(1)由题意知false的定义域是false
因为false,
令false得false(舍),
false由false得false
所以false的单调递减区间是false,单调递增区间是false
(2)因为false,false恒成立,
有false,false,
即false在false上恒成立,
所以false在false上的最小值false.
由(1)知:
① 当false,即false时,false在false上单调递减,
false,
即false,false,false,
② 当false,即false时,false在false上单调递增,
false,即false
③ 当false,即false时,
false在false上单调递减,在false上单调递增,
因为false,false,
从而false,此时false成立,
综上:a的取值范围为false.
【点睛】
用导数求函数的单调区间或判断函数的单调性问题时应注意如下几方面:
(1)在利用导数讨论函数的单调区间时,首先要确定函数的定义域;
(2)不能随意将函数的2个独立的单调递增(或递减)区间写成并集形式;
(3)利用导数解决含参函数的单调性问题时,一般将其转化为不等式恒成立问题,解题过程中要注意分类讨论和数形结合思想的应用.
22.(1)false;false;(2)4.
【分析】
(1)false两边同时乘以false,由false,false可得直角坐标方程以及点P的直角坐标.
(2)将直线的参数方程代入C方程,利用参数false的几何意义即可求解.
【详解】
解:(1)由false,得false,
又false,false,∴false,
即曲线C的直角坐标方程为false,
点P的直角坐标为false.
(2)把直线l的方程代入C方程,整理得false,
false,
设A、B对应的参数分别是false、false,则false,
于是false
23.(1)false;(2)false.
【分析】
(1)分段讨论去绝对值解不等式即可;
(2)先将题意转化为false没有实数根, 再求false值域,利用false取值为false值域的补集,计算即得结果.
【详解】
解:(1)当false时,false,
得false,所以false;
当false时,false,
得false,所以false;
当false时,false,得false,所以false.
综上,原不等式的解集为false;
(2)方程false没有实数根,即false没有实数根,
令false,
当且仅当false时,即false时等号成立,即false值域为false,
若false没有实数根,则false,即false,
所以实数m的取值范围为false.
【点睛】
方法点睛:
1、绝对值不等式的解法:
(1)利用绝对值不等式的几何意义求解,体现了数形结合的思想;
(2)利于“零点分段法”去绝对值进行求解,体现了分类讨论思想;
(3)通过构造函数,利用函数图象求解,体现了函数与方程思想.
2、不等式恒成立问题通常可转化成函数最值来处理.
同课章节目录
