16.1二次根式的性质 课件-2020-2021学年人教版八年级数学下册(共19张)
文档属性
| 名称 | 16.1二次根式的性质 课件-2020-2021学年人教版八年级数学下册(共19张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-22 13:59:36 | ||
图片预览




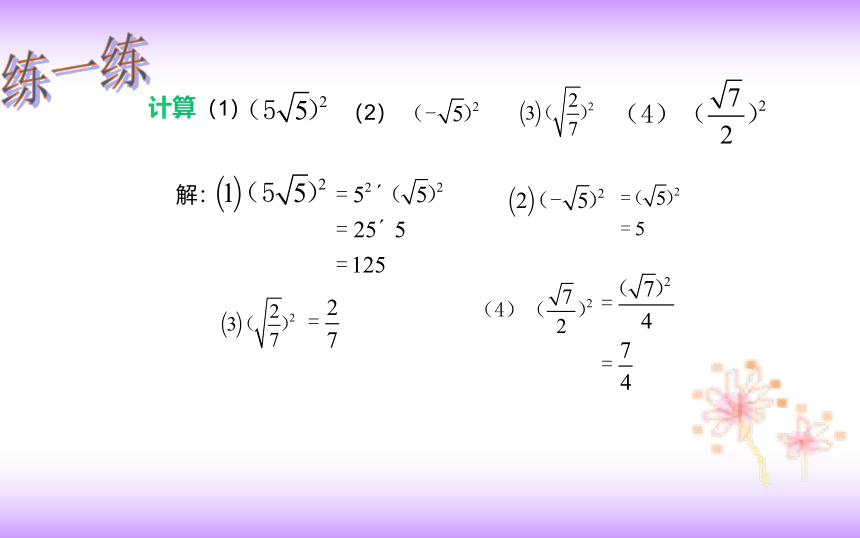


文档简介
空白演示
单击输入您的封面副标题
16.1 二次根式的性质
人教版数学八年级下册
当 >0时, 表示 的算术平方
根,因此 >___;当 =0时, 表示0
的算术平方根,因此 =___.这就是
说,当 ≥____时, ≥ ??? .即
( ≥0)是一个非负数.
0
0
0
0
温故知新
4
9
0.01
2
30
二次根式的性质探究1
问题1:利用算术平方根的意义填空
运算顺序:先开方,再平方
归纳
(a≥0)
探究新知
=4×5
=20
例2 计算:
(1) (2)
解:⑴ =
⑵ =
1.5
例题讲解
计算(1)
(2)
解:
练一练
二次根式的性质探究2
问题2:利用算术平方根的意义填空
运算顺序:先平方,再开方
0.01
0
4
归纳
4
探究新知
例3:化简
解:(1)原式=
(2)原式=
(3)原式=
(4)原式=
例题讲解
计算:
解:
练一练
二次根式的性质1、2
比较分析 和
{5940675A-B579-460E-94D1-54222C63F5DA}
读法
运算顺序
a的取值范围
运算结果
先开方,后平方
先平方,后开方
a≥0
a取全体实数
a
∣a∣
a的算术平方根的平方
a的平方的算术平方根
求平方直“抵消”
求根就取绝对值
探究新知
10
5
7
18
( x﹤ y)
∵x∴x-y<0
∴
1.计算:
巩固练习
2.对于性质 ,逆向思考可得:
(a≥0)
(a≥0),
请根据这一结论完成填空:
(1) ;(2) .
2
?
3
?
????2-3=????2-
?
=(x+3)(x-3)
?
(3)在实数范围内分解因式:x2-3
巩固练习
3.若 ,则x的取值范围为 ( )
(A) x≤1 (B) x≥1 (C) 0≤x≤1 (D)一切有理数
A
m ≤ 4
11、8、3
巩固练习
4.化简及求值:
巩固练习
5..若a.b为实数,且
求 的值
解:
巩固练习
6.已知a,b,c为△ABC的三边长,化简:
+
-
巩固练习
7.实数p在数轴上的位置如图所示,化简
巩固练习
1、 ( ≥0)是一个_______数.
2、 = ____ ( ≥ ).
= ____ ( ≥ ).
3、 与 的区别是
.
非负
0
0
中的a可以是一
切实数 ,而 中 必须是大于或等于零.
即 = ,.
=| |
( )
≥
0
课堂小结
布置作业
教科书5页,习 题16.1 2,4题
教科书第60页第3、6题
布置作业
再见
单击输入您的封面副标题
16.1 二次根式的性质
人教版数学八年级下册
当 >0时, 表示 的算术平方
根,因此 >___;当 =0时, 表示0
的算术平方根,因此 =___.这就是
说,当 ≥____时, ≥ ??? .即
( ≥0)是一个非负数.
0
0
0
0
温故知新
4
9
0.01
2
30
二次根式的性质探究1
问题1:利用算术平方根的意义填空
运算顺序:先开方,再平方
归纳
(a≥0)
探究新知
=4×5
=20
例2 计算:
(1) (2)
解:⑴ =
⑵ =
1.5
例题讲解
计算(1)
(2)
解:
练一练
二次根式的性质探究2
问题2:利用算术平方根的意义填空
运算顺序:先平方,再开方
0.01
0
4
归纳
4
探究新知
例3:化简
解:(1)原式=
(2)原式=
(3)原式=
(4)原式=
例题讲解
计算:
解:
练一练
二次根式的性质1、2
比较分析 和
{5940675A-B579-460E-94D1-54222C63F5DA}
读法
运算顺序
a的取值范围
运算结果
先开方,后平方
先平方,后开方
a≥0
a取全体实数
a
∣a∣
a的算术平方根的平方
a的平方的算术平方根
求平方直“抵消”
求根就取绝对值
探究新知
10
5
7
18
( x﹤ y)
∵x
∴
1.计算:
巩固练习
2.对于性质 ,逆向思考可得:
(a≥0)
(a≥0),
请根据这一结论完成填空:
(1) ;(2) .
2
?
3
?
????2-3=????2-
?
=(x+3)(x-3)
?
(3)在实数范围内分解因式:x2-3
巩固练习
3.若 ,则x的取值范围为 ( )
(A) x≤1 (B) x≥1 (C) 0≤x≤1 (D)一切有理数
A
m ≤ 4
11、8、3
巩固练习
4.化简及求值:
巩固练习
5..若a.b为实数,且
求 的值
解:
巩固练习
6.已知a,b,c为△ABC的三边长,化简:
+
-
巩固练习
7.实数p在数轴上的位置如图所示,化简
巩固练习
1、 ( ≥0)是一个_______数.
2、 = ____ ( ≥ ).
= ____ ( ≥ ).
3、 与 的区别是
.
非负
0
0
中的a可以是一
切实数 ,而 中 必须是大于或等于零.
即 = ,.
=| |
( )
≥
0
课堂小结
布置作业
教科书5页,习 题16.1 2,4题
教科书第60页第3、6题
布置作业
再见
