17.1勾股定理(1)作业-2020-2021学年人教版八年级数学下册(word版含答案)
文档属性
| 名称 | 17.1勾股定理(1)作业-2020-2021学年人教版八年级数学下册(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 229.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-22 14:39:12 | ||
图片预览

文档简介
17.1勾股定理作业
一、选择题
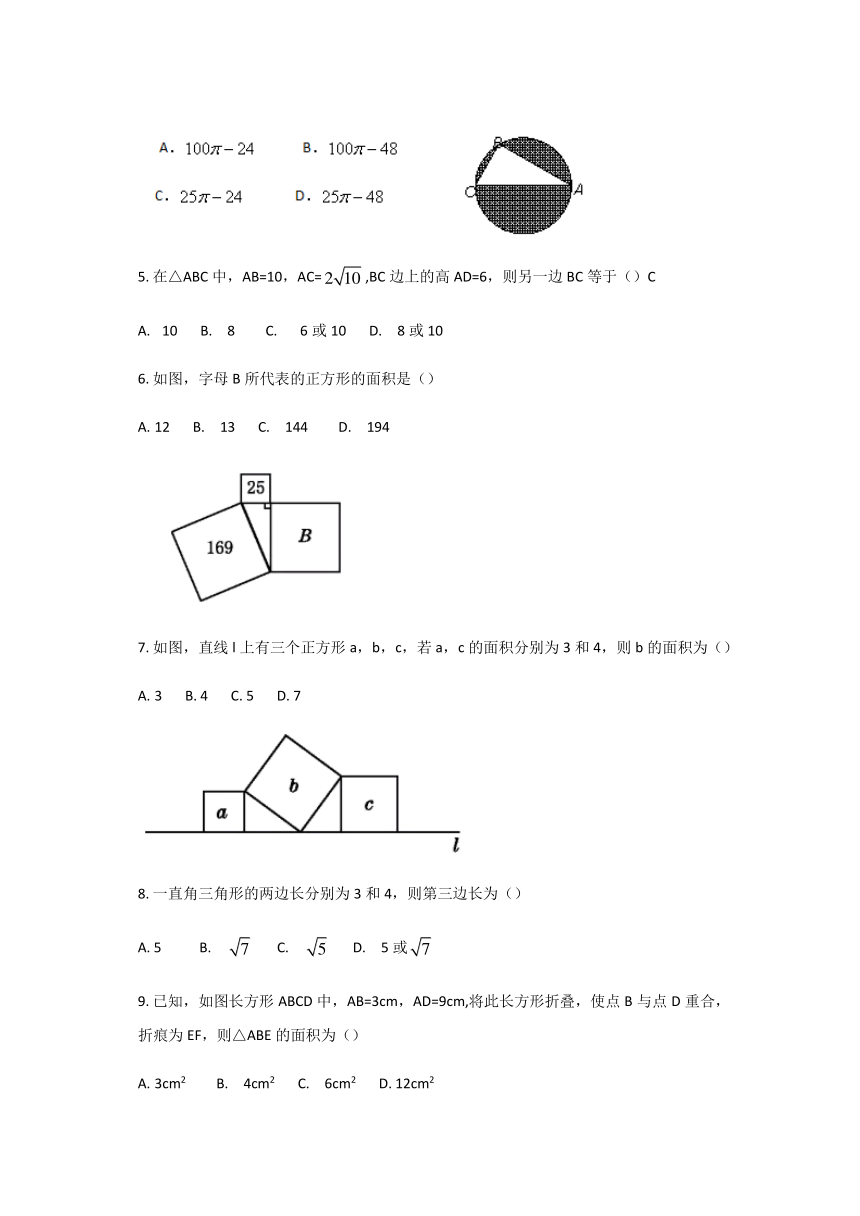
如图,以直角三角形的三边a,b,c为边或直径,分别向外作等边三角形,半圆,等腰直角三角形和正方形,上述四种情况的面积关系满足S1+S2=S3的图形个数是()
1 B. 2 C. 3 D . 4
如图,正方形网格中,每个小正方形的边长为1,则在△ABC中,边长是整数的边有()
0条 B. 1条 C. 2条 D. 3条
如图,在△ABC中,AB=AC,AD是∠BAC的平分线,已知AB=5,AD=3,则BC的长为()
5 B. 6 C. 8 D. 10
如图,在Rt△ABC中,∠B=900,以AC为直径的圆恰好过点B,AB=8,BC=6,则阴影部分的面积是()
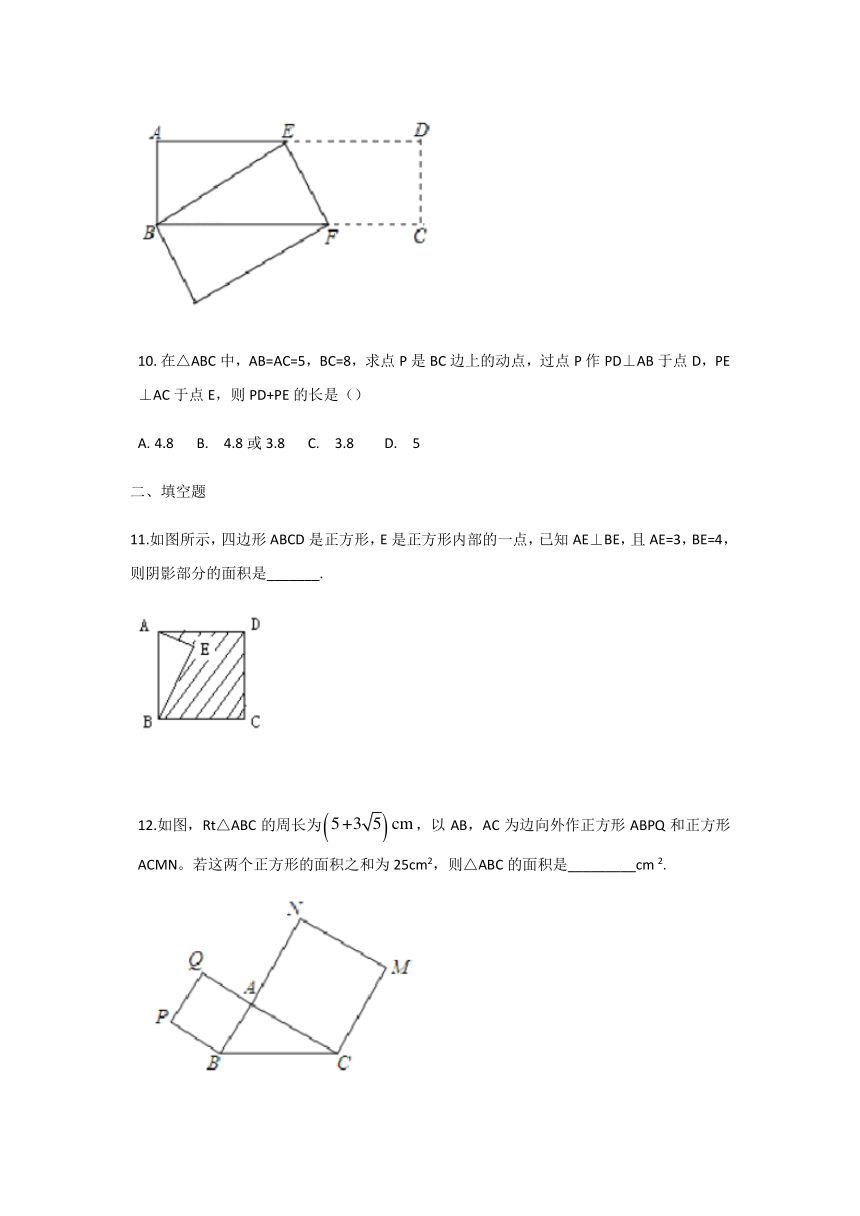
在△ABC中,AB=10,AC=,BC边上的高AD=6,则另一边BC等于()C
10 B. 8 C. 6或10 D. 8或10
如图,字母B所代表的正方形的面积是()
12 B. 13 C. 144 D. 194
如图,直线l上有三个正方形a,b,c,若a,c的面积分别为3和4,则b的面积为()
3 B. 4 C. 5 D. 7
一直角三角形的两边长分别为3和4,则第三边长为()
A. 5 B. C. D. 5或
已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为()
3cm2 B. 4cm2 C. 6cm2 D. 12cm2
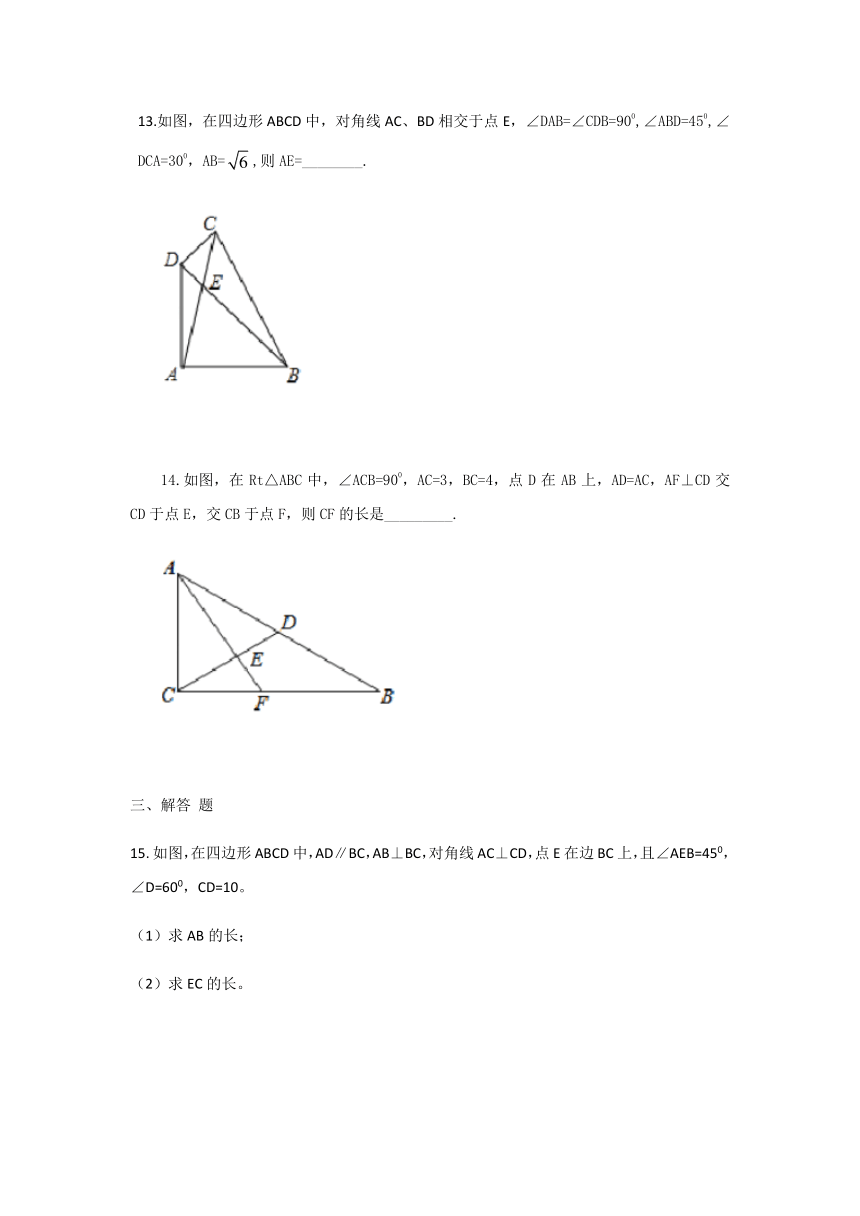
在△ABC中,AB=AC=5,BC=8,求点P是BC边上的动点,过点P作PD⊥AB于点D,PE⊥AC于点E,则PD+PE的长是()
4.8 B. 4.8或3.8 C. 3.8 D. 5
填空题
11.如图所示,四边形ABCD是正方形,E是正方形内部的一点,已知AE⊥BE,且AE=3,BE=4,则阴影部分的面积是_______.
12.如图,Rt△ABC的周长为,以AB,AC为边向外作正方形ABPQ和正方形ACMN。若这两个正方形的面积之和为25cm2,则△ABC的面积是_________cm 2.
13.如图,在四边形ABCD中,对角线AC、BD相交于点E,∠DAB=∠CDB=900,∠ABD=450,∠DCA=300,AB=,则AE=________.
14.如图,在Rt△ABC中,∠ACB=900,AC=3,BC=4,点D在AB上,AD=AC,AF⊥CD交CD于点E,交CB于点F,则CF的长是_________.
解答 题
如图,在四边形ABCD中,AD∥BC,AB⊥BC,对角线AC⊥CD,点E在边BC上,且∠AEB=450,∠D=600,CD=10。
求AB的长;
求EC的长。
如图,在△ABC中,CD⊥AB于D,AC=4,BC=3,DB=.
求DC的长;
求AB的长。
参考答案
选择题
1 2 3 4 5 6 7 8 9 10
D C C C C C C D C A
填空题
19
5(cm)2
解析:设AB=c,AC=b,BC=a
∵两个正方形的面积之和为25cm2
∴
∵
∴a=5
∵Rt△ABC的周长为
∴b+c=
∵(b+c)2=
∴2ab=45-25=20
∴ S△ABC的面积=ab=5(cm)2
2
解析:过A作AF⊥BD,垂足为F
∵∠ABD=450,∠DAB=900
∴∠ADB=∠ABD
∴AD=AB=
∴DB=2
∴AF=
∵∠CDB=∠AFD=900
∴CD∥AF
∴∠EAF=∠ECD=300
∴AE=2EF
根据勾股定理 可得:AE=2
解析:连接DF
∵AD=AC,AF⊥CD
∴CE=DE
∴CF=DF
∵AF=AF
∴△ACF≌△ADF
∴∠ADF=∠ACF=900
∴∠BDF=900
又∵∠ACB=900,AC=3,BC=4
∴AB=5
∴BD=AB-AD=2
∵DF2+DB2=BF2
∴FC2+4=(4-FC)2
解得 FC=
解答 题
15.解析:(1)∵AC⊥CD,∠D=600
∴∠DAC=300
∴AD=2CD=20
∴AC=
∵AD∥BC
∴∠ACB=∠∠DAC=300
∵AB⊥BC
∴AB=AC=5
(2) ∵AB⊥BC,∠AEB=450,
∴∠BAE=∠AEB=450
∴BE=AB=5
∵BC=
∴EC=BC-EB=15-5
16.解析:(1)∵CD⊥AB
∴∠CDB=∠CDA=900
∵,BC=3,DB=
∴DC=
(2)∵,AC=4,DC=
∴AD=
∴AB=AD+DB=+=5
一、选择题
如图,以直角三角形的三边a,b,c为边或直径,分别向外作等边三角形,半圆,等腰直角三角形和正方形,上述四种情况的面积关系满足S1+S2=S3的图形个数是()
1 B. 2 C. 3 D . 4
如图,正方形网格中,每个小正方形的边长为1,则在△ABC中,边长是整数的边有()
0条 B. 1条 C. 2条 D. 3条
如图,在△ABC中,AB=AC,AD是∠BAC的平分线,已知AB=5,AD=3,则BC的长为()
5 B. 6 C. 8 D. 10
如图,在Rt△ABC中,∠B=900,以AC为直径的圆恰好过点B,AB=8,BC=6,则阴影部分的面积是()
在△ABC中,AB=10,AC=,BC边上的高AD=6,则另一边BC等于()C
10 B. 8 C. 6或10 D. 8或10
如图,字母B所代表的正方形的面积是()
12 B. 13 C. 144 D. 194
如图,直线l上有三个正方形a,b,c,若a,c的面积分别为3和4,则b的面积为()
3 B. 4 C. 5 D. 7
一直角三角形的两边长分别为3和4,则第三边长为()
A. 5 B. C. D. 5或
已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为()
3cm2 B. 4cm2 C. 6cm2 D. 12cm2
在△ABC中,AB=AC=5,BC=8,求点P是BC边上的动点,过点P作PD⊥AB于点D,PE⊥AC于点E,则PD+PE的长是()
4.8 B. 4.8或3.8 C. 3.8 D. 5
填空题
11.如图所示,四边形ABCD是正方形,E是正方形内部的一点,已知AE⊥BE,且AE=3,BE=4,则阴影部分的面积是_______.
12.如图,Rt△ABC的周长为,以AB,AC为边向外作正方形ABPQ和正方形ACMN。若这两个正方形的面积之和为25cm2,则△ABC的面积是_________cm 2.
13.如图,在四边形ABCD中,对角线AC、BD相交于点E,∠DAB=∠CDB=900,∠ABD=450,∠DCA=300,AB=,则AE=________.
14.如图,在Rt△ABC中,∠ACB=900,AC=3,BC=4,点D在AB上,AD=AC,AF⊥CD交CD于点E,交CB于点F,则CF的长是_________.
解答 题
如图,在四边形ABCD中,AD∥BC,AB⊥BC,对角线AC⊥CD,点E在边BC上,且∠AEB=450,∠D=600,CD=10。
求AB的长;
求EC的长。
如图,在△ABC中,CD⊥AB于D,AC=4,BC=3,DB=.
求DC的长;
求AB的长。
参考答案
选择题
1 2 3 4 5 6 7 8 9 10
D C C C C C C D C A
填空题
19
5(cm)2
解析:设AB=c,AC=b,BC=a
∵两个正方形的面积之和为25cm2
∴
∵
∴a=5
∵Rt△ABC的周长为
∴b+c=
∵(b+c)2=
∴2ab=45-25=20
∴ S△ABC的面积=ab=5(cm)2
2
解析:过A作AF⊥BD,垂足为F
∵∠ABD=450,∠DAB=900
∴∠ADB=∠ABD
∴AD=AB=
∴DB=2
∴AF=
∵∠CDB=∠AFD=900
∴CD∥AF
∴∠EAF=∠ECD=300
∴AE=2EF
根据勾股定理 可得:AE=2
解析:连接DF
∵AD=AC,AF⊥CD
∴CE=DE
∴CF=DF
∵AF=AF
∴△ACF≌△ADF
∴∠ADF=∠ACF=900
∴∠BDF=900
又∵∠ACB=900,AC=3,BC=4
∴AB=5
∴BD=AB-AD=2
∵DF2+DB2=BF2
∴FC2+4=(4-FC)2
解得 FC=
解答 题
15.解析:(1)∵AC⊥CD,∠D=600
∴∠DAC=300
∴AD=2CD=20
∴AC=
∵AD∥BC
∴∠ACB=∠∠DAC=300
∵AB⊥BC
∴AB=AC=5
(2) ∵AB⊥BC,∠AEB=450,
∴∠BAE=∠AEB=450
∴BE=AB=5
∵BC=
∴EC=BC-EB=15-5
16.解析:(1)∵CD⊥AB
∴∠CDB=∠CDA=900
∵,BC=3,DB=
∴DC=
(2)∵,AC=4,DC=
∴AD=
∴AB=AD+DB=+=5
