18.1.1勾股定理
图片预览



文档简介
(共27张PPT)
1、你曾见过这个图案吗
活动1 欣赏图片 了解历史
赵爽弦图
这个图案是3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称之为“赵爽弦图”
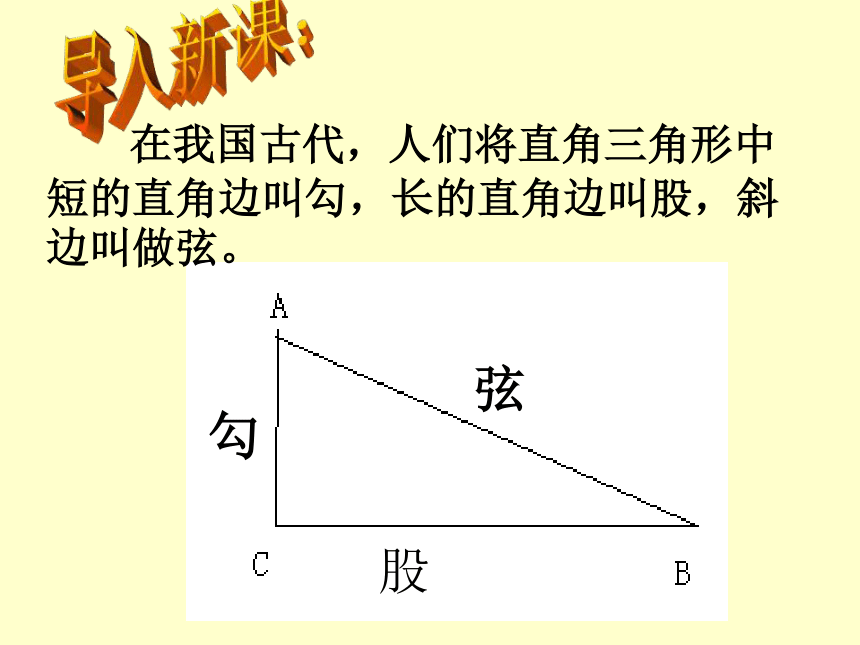
勾
股
弦
在我国古代,人们将直角三角形中短的直角边叫勾,长的直角边叫股,斜边叫做弦。
活动2、 探索勾股定理
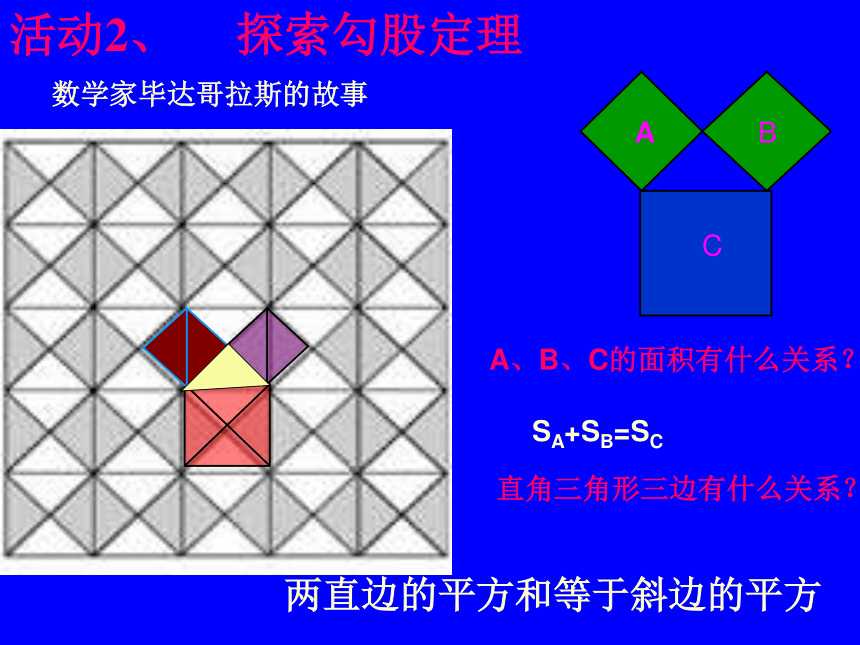
A
B
C
A、B、C的面积有什么关系?
SA+SB=SC
直角三角形三边有什么关系?
两直边的平方和等于斜边的平方
数学家毕达哥拉斯的故事
探索勾股定理
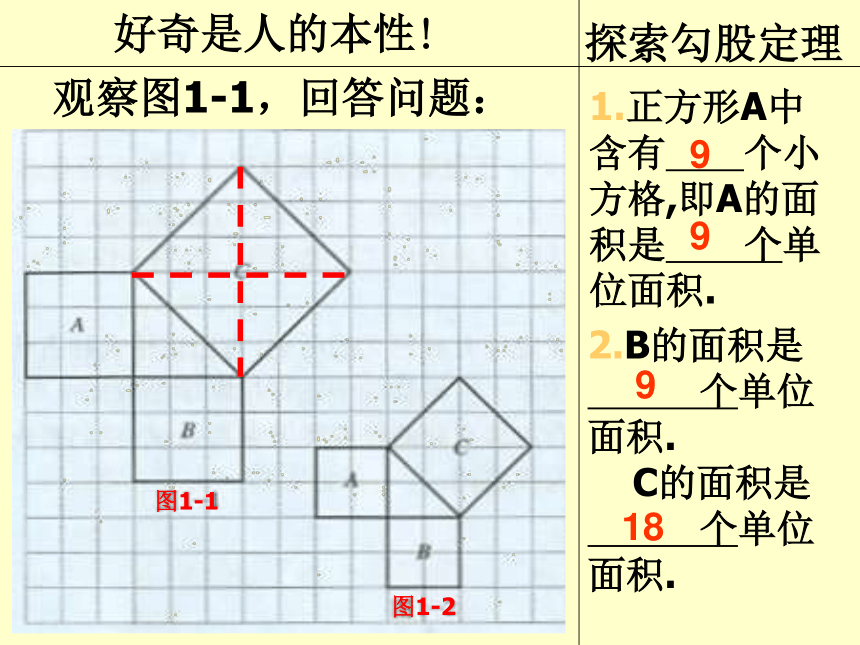
观察图1-1,回答问题:
1.正方形A中含有 个小方格,即A的面积是 个单位面积.
2.B的面积是 个单位面积. C的面积是 个单位面积.
图1-1
图1-2
好奇是人的本性!
9
9
18
9
探索勾股定理
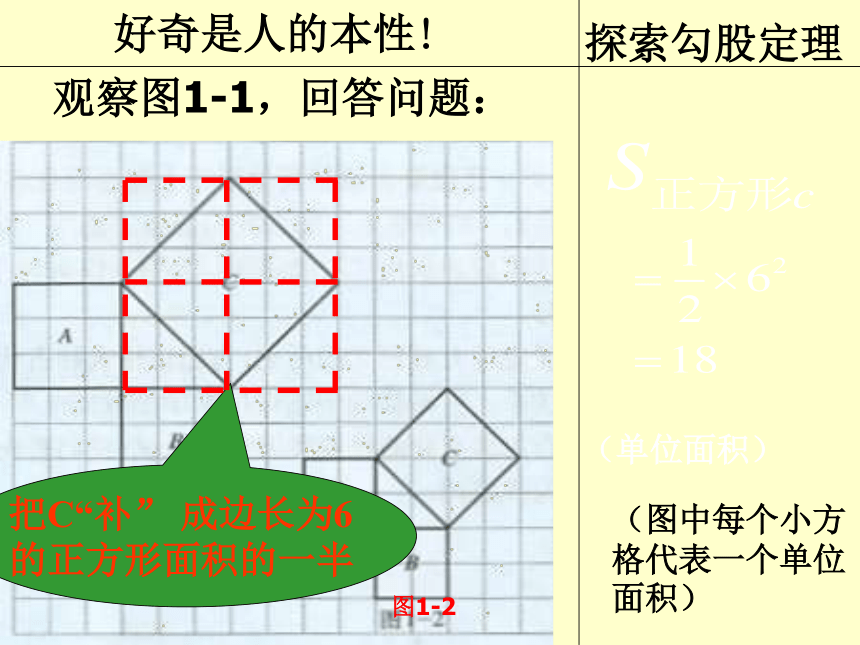
观察图1-1,回答问题:
图1-1
图1-2
好奇是人的本性!
(图中每个小方格代表一个单位面积)
(单位面积)
把C“补” 成边长为6的正方形面积的一半
SA+SB=SC
B
C
a
b
c
A
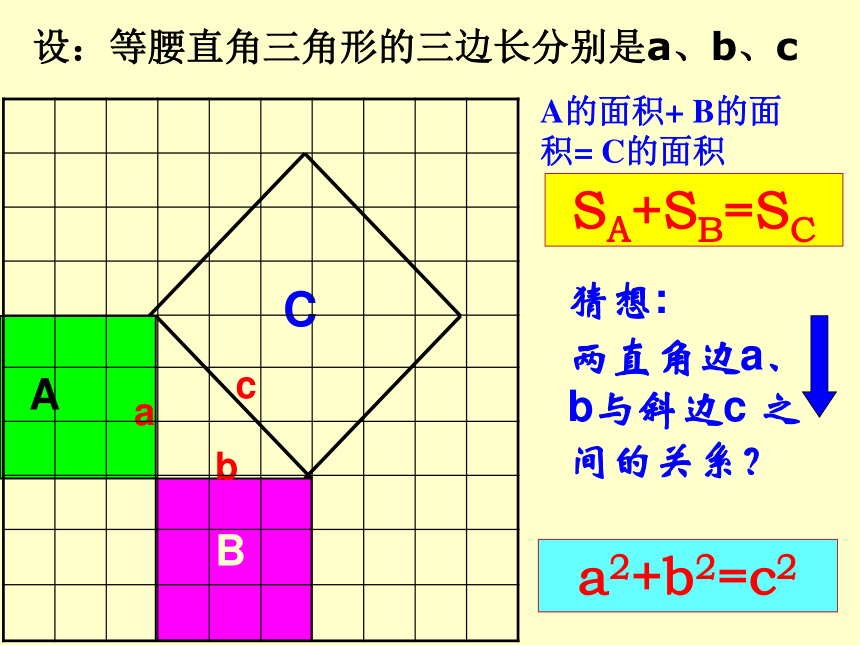
设:等腰直角三角形的三边长分别是a、b、c
猜想:
两直角边a、b与斜边c 之间的关系?
A的面积+ B的面积= C的面积
a2+b2=c2
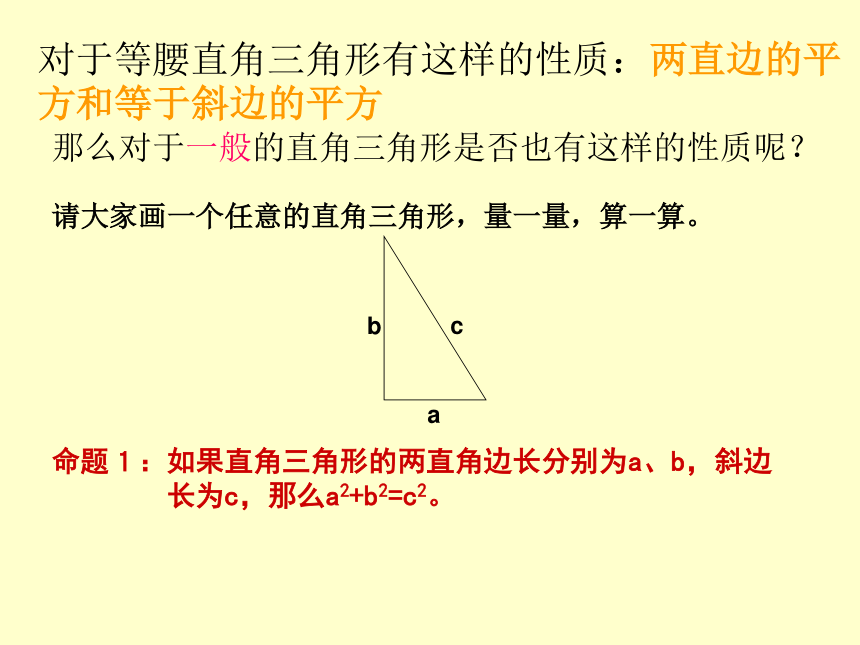
对于等腰直角三角形有这样的性质:两直边的平方和等于斜边的平方
那么对于一般的直角三角形是否也有这样的性质呢?
请大家画一个任意的直角三角形,量一量,算一算。
命题1:如果直角三角形的两直角边长分别为a、b,斜边
长为c,那么a2+b2=c2。
a
b
c
A
B
C
图1-3
A
B
C
图1-4
2.观察右边两个图并填写下表:
A的面积 B的面积 C的面积
图1-3
图1-4
16
9
25
4
9
13
你是怎样得到表中的结果的?与同伴交流交流.
A
B
C
图1-3
A
B
C
图1-4
3.三个正方形A,B,C面积之间有什么关系?
SA+SB=SC
即:两条直角边上的正方形面积之和等于斜边上的正方形的面积.
A
B
C
a
c
b
SA+SB=SC
设:直角三角形的三边长分别是a、b、c
a2+b2=c2
两条直角边上的正方形面积之和等于斜边上的正方形的面积.
c
b a
依据科学理论的证实:
我国汉代的数学家赵爽指出:四个全等的直角三角形如下拼成一个中空的正方形,由大正方形的面积等于小正方形的面积与4个直角三角形的面积和得:
直角三角形两直角边的平方和等于斜边的平方
a
b
你能用这个图试着证明勾股定理吗?
赵爽弦图
赵爽弦图的证法
化简得: c2 =a2+ b2.
定理:经过证明被确认为正确的命题叫做定理。
勾股定理:
如果直角三角形的两直角边长分别为 a、b,斜边为c,那么a2+b2=c2。
如图,在Rt△ABC中,∠C= 90°,则
a2+b2=c2
A
B
C
股b
勾 a
弦c
勾股定理的各种表达式:
在RT△ABC中,∠C=90°, ∠A 、∠B、 ∠C的对边分别为a 、b 、c ,则:
c2=a2+b2
a2=c2-b2
b2=c2-a2
c2=a2+b2
a2=c2-b2
b2=c2-a2
c=
a=
b=
练习:
1、求下列图中字母所表示的正方形的面积
=625
225
400
A
225
81
B
=144
2、求出下列直角三角形中未知边的长度
6
8
x
5
x
13
解:由勾股定理得:
x2 =36+64
x2 =100
x2=62+82
∴ x=10
∵ x2+52=132
∴ x2=132-52
x2 =169-25
x2 =144
∴ x=12
∵ x > 0
∵ x > 0
1) 在直角三角形中,两条直角边分别为a,b, 斜边为c,则c2=____
a2+b2
2) 在RT△ABC中∠C=90°,
⑴若a=4,b=3,则c=____
⑵若c=13,b=5,则a=____
⑶ 若 c=17,a=8,则b=____
5
12
15
一 填空题:
(3 ) 等边三角形的边长为12,
则它的高为______
(4) 在直角三角形中,如果有两边 为3,4,那么另一边为_________
5或
⑶一个长方形的长是宽的2 倍,其对角线的长是5㎝,那么它的宽是( )
A ㎝ B ㎝ C ㎝ D ㎝
二 选择题:
⑴如果直角三角形的一个锐角为30度,斜边长是2 ㎝ ,那么直角三角形的其它两边长是( )
A 1, B 1 ,3 C 1, D 1 ,5
⑵如图,在RT△ABC中,∠C=90°,
∠B=45°,AC=1,则AB=( )
A 2, B 1, C , D
A
C
B
A
B
C
(4)、放学以后,小红和小颖从学校分手,分别沿着东方向和南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖用20分钟到家,小红和小颖家的距离为 ( )
A、600米 B、800米
C、1000米 D、不能确定
(5)、直角三角形两直角边分别为5厘米、12厘米,那么斜边上的高是 ( )
A、6厘米 B、 8厘米
C、 80/13厘米; D、 60/13厘米;
C
D
探索勾股定理
1、想一想
我们有:
三、解决问题:
46
b=58
a=46
58
c
c2=a2+b2 =462+582
=5480
而742=5476
由勾股定理得:
在误差范围内
D
A
B
C
2、蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)
G
F
E
某楼房三楼失火,消防队员赶来救火,了解到每层楼高2米,消防队员取来7米长的云梯,如果梯子的底部离墙基的距离是2.5米,请问消防队能否进入三楼灭火
应用举例
解:如图,在Rt△ABC中,∠C=90°, AC=6米 ,
BC=2米,则AB= ≈6.3
因为7米大于6.3米
所以消防队能进入三楼灭火
1)本节课我们学习了什么
3)了解用面积法证明勾股定理
勾股定理
2)利用勾股定理,
已知直角三角形
的某两边长,会根据条件求另一边
2、通过书籍和网络查阅有关资料,了解勾股定理的历史背景
和意义(如课本P65)
1、P69-70第1、2题
1、你曾见过这个图案吗
活动1 欣赏图片 了解历史
赵爽弦图
这个图案是3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称之为“赵爽弦图”
勾
股
弦
在我国古代,人们将直角三角形中短的直角边叫勾,长的直角边叫股,斜边叫做弦。
活动2、 探索勾股定理
A
B
C
A、B、C的面积有什么关系?
SA+SB=SC
直角三角形三边有什么关系?
两直边的平方和等于斜边的平方
数学家毕达哥拉斯的故事
探索勾股定理
观察图1-1,回答问题:
1.正方形A中含有 个小方格,即A的面积是 个单位面积.
2.B的面积是 个单位面积. C的面积是 个单位面积.
图1-1
图1-2
好奇是人的本性!
9
9
18
9
探索勾股定理
观察图1-1,回答问题:
图1-1
图1-2
好奇是人的本性!
(图中每个小方格代表一个单位面积)
(单位面积)
把C“补” 成边长为6的正方形面积的一半
SA+SB=SC
B
C
a
b
c
A
设:等腰直角三角形的三边长分别是a、b、c
猜想:
两直角边a、b与斜边c 之间的关系?
A的面积+ B的面积= C的面积
a2+b2=c2
对于等腰直角三角形有这样的性质:两直边的平方和等于斜边的平方
那么对于一般的直角三角形是否也有这样的性质呢?
请大家画一个任意的直角三角形,量一量,算一算。
命题1:如果直角三角形的两直角边长分别为a、b,斜边
长为c,那么a2+b2=c2。
a
b
c
A
B
C
图1-3
A
B
C
图1-4
2.观察右边两个图并填写下表:
A的面积 B的面积 C的面积
图1-3
图1-4
16
9
25
4
9
13
你是怎样得到表中的结果的?与同伴交流交流.
A
B
C
图1-3
A
B
C
图1-4
3.三个正方形A,B,C面积之间有什么关系?
SA+SB=SC
即:两条直角边上的正方形面积之和等于斜边上的正方形的面积.
A
B
C
a
c
b
SA+SB=SC
设:直角三角形的三边长分别是a、b、c
a2+b2=c2
两条直角边上的正方形面积之和等于斜边上的正方形的面积.
c
b a
依据科学理论的证实:
我国汉代的数学家赵爽指出:四个全等的直角三角形如下拼成一个中空的正方形,由大正方形的面积等于小正方形的面积与4个直角三角形的面积和得:
直角三角形两直角边的平方和等于斜边的平方
a
b
你能用这个图试着证明勾股定理吗?
赵爽弦图
赵爽弦图的证法
化简得: c2 =a2+ b2.
定理:经过证明被确认为正确的命题叫做定理。
勾股定理:
如果直角三角形的两直角边长分别为 a、b,斜边为c,那么a2+b2=c2。
如图,在Rt△ABC中,∠C= 90°,则
a2+b2=c2
A
B
C
股b
勾 a
弦c
勾股定理的各种表达式:
在RT△ABC中,∠C=90°, ∠A 、∠B、 ∠C的对边分别为a 、b 、c ,则:
c2=a2+b2
a2=c2-b2
b2=c2-a2
c2=a2+b2
a2=c2-b2
b2=c2-a2
c=
a=
b=
练习:
1、求下列图中字母所表示的正方形的面积
=625
225
400
A
225
81
B
=144
2、求出下列直角三角形中未知边的长度
6
8
x
5
x
13
解:由勾股定理得:
x2 =36+64
x2 =100
x2=62+82
∴ x=10
∵ x2+52=132
∴ x2=132-52
x2 =169-25
x2 =144
∴ x=12
∵ x > 0
∵ x > 0
1) 在直角三角形中,两条直角边分别为a,b, 斜边为c,则c2=____
a2+b2
2) 在RT△ABC中∠C=90°,
⑴若a=4,b=3,则c=____
⑵若c=13,b=5,则a=____
⑶ 若 c=17,a=8,则b=____
5
12
15
一 填空题:
(3 ) 等边三角形的边长为12,
则它的高为______
(4) 在直角三角形中,如果有两边 为3,4,那么另一边为_________
5或
⑶一个长方形的长是宽的2 倍,其对角线的长是5㎝,那么它的宽是( )
A ㎝ B ㎝ C ㎝ D ㎝
二 选择题:
⑴如果直角三角形的一个锐角为30度,斜边长是2 ㎝ ,那么直角三角形的其它两边长是( )
A 1, B 1 ,3 C 1, D 1 ,5
⑵如图,在RT△ABC中,∠C=90°,
∠B=45°,AC=1,则AB=( )
A 2, B 1, C , D
A
C
B
A
B
C
(4)、放学以后,小红和小颖从学校分手,分别沿着东方向和南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖用20分钟到家,小红和小颖家的距离为 ( )
A、600米 B、800米
C、1000米 D、不能确定
(5)、直角三角形两直角边分别为5厘米、12厘米,那么斜边上的高是 ( )
A、6厘米 B、 8厘米
C、 80/13厘米; D、 60/13厘米;
C
D
探索勾股定理
1、想一想
我们有:
三、解决问题:
46
b=58
a=46
58
c
c2=a2+b2 =462+582
=5480
而742=5476
由勾股定理得:
在误差范围内
D
A
B
C
2、蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)
G
F
E
某楼房三楼失火,消防队员赶来救火,了解到每层楼高2米,消防队员取来7米长的云梯,如果梯子的底部离墙基的距离是2.5米,请问消防队能否进入三楼灭火
应用举例
解:如图,在Rt△ABC中,∠C=90°, AC=6米 ,
BC=2米,则AB= ≈6.3
因为7米大于6.3米
所以消防队能进入三楼灭火
1)本节课我们学习了什么
3)了解用面积法证明勾股定理
勾股定理
2)利用勾股定理,
已知直角三角形
的某两边长,会根据条件求另一边
2、通过书籍和网络查阅有关资料,了解勾股定理的历史背景
和意义(如课本P65)
1、P69-70第1、2题
