2.5.1一元一次不等式与一次函数的关系-2020-2021学年北师大版八年级数学下册课件(共13张)
文档属性
| 名称 | 2.5.1一元一次不等式与一次函数的关系-2020-2021学年北师大版八年级数学下册课件(共13张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 156.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-22 00:00:00 | ||
图片预览



文档简介
第二章 一元一次不等式
与一元一次不等式组
2.5 一元一次不等式与一次函数
第1课时 一元一次不等式与一次函数的关系
一、复习回顾
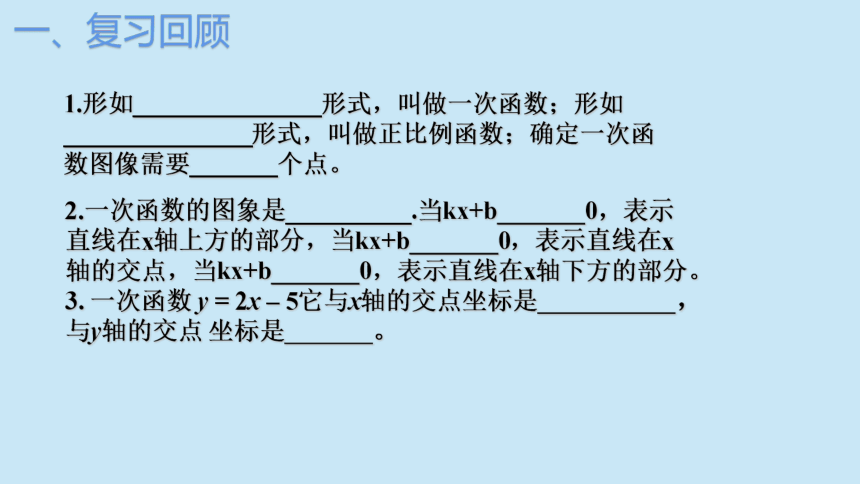
1.形如_______________形式,叫做一次函数;形如_______________形式,叫做正比例函数;确定一次函数图像需要_______个点。
2.一次函数的图象是__________.当kx+b_______0,表示直线在x轴上方的部分,当kx+b_______0,表示直线在x轴的交点,当kx+b_______0,表示直线在x轴下方的部分。
3. 一次函数 y = 2x – 5它与x轴的交点坐标是 ,与y轴的交点 坐标是 。
二、新课导入
小华准备将平时的零用钱储存起来,他已经存有300元,现在起每月存50元.小华的同学小丽以前没有存过零用钱,在听说小华存零用钱后,表示从现在起每月存70元,争取超过小华.根据以上信息,你能帮助小丽计算出她需要多久才能超过小华吗?
三、新课讲授
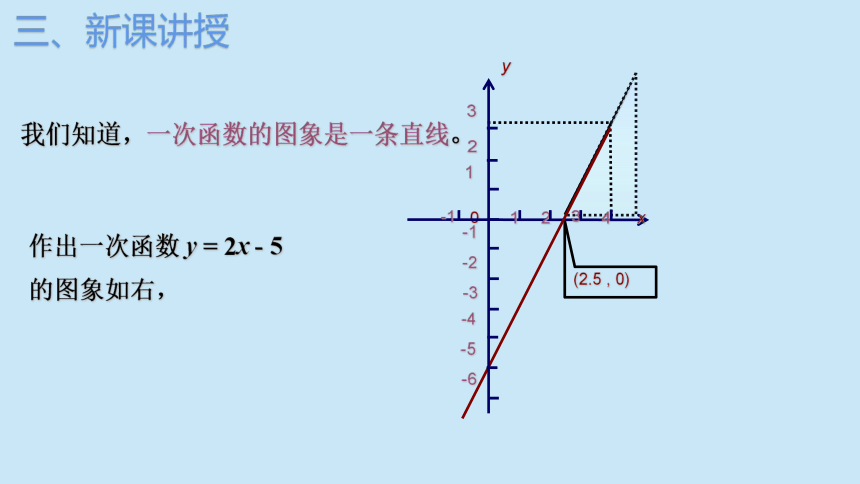
我们知道,一次函数的图象是一条直线。
作出一次函数 y = 2x - 5
的图象如右,
(2.5 , 0)
0
x
1
2
3
-1
4
1
-1
-2
3
-4
-3
2
-5
-6
y
观察图象回答下列问题:
x > 2.5 时
x = 2.5 时
x < 2.5 时
x > 4 时
(2.5 , 0)
0
x
1
2
3
-1
4
1
-1
-2
3
-4
-3
2
-5
-6
y
(1) x 取哪些值时, 2x-5=0 ?
(2) x 取哪些值时, 2x-5>0 ?
(3) x 取哪些值时, 2x-5<0 ?
(4) x 取哪些值时, 2x-5 >3 ?
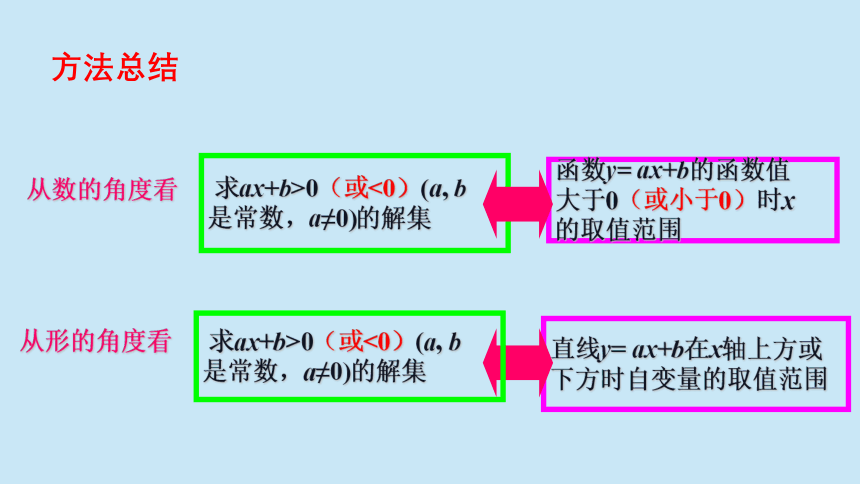
求ax+b>0(或<0)(a, b
是常数,a≠0)的解集
函数y= ax+b的函数值
大于0(或小于0)时x
的取值范围
直线y= ax+b在x轴上方或
下方时自变量的取值范围
从数的角度看
从形的角度看
求ax+b>0(或<0)(a, b
是常数,a≠0)的解集
方法总结
如果 y=-2x-5 , 那么当 x 取何值时 , y>0 ?
你解答此道题, 可有几种方法 ?
用“函数图象法”及“解不等式法”解函数问题
法一:
将函数问题转化为不等式问题(从数的角度看)
即 解不等式
-2x- 5 > 0 ;
法二:
图象法(从形的角度看)
x
y
-1
-2
-3
-4
-5
1
-1
-2
-3
-4
-5
-6
1
2
3
由图易知,
当 x
< -2.5时 y>0 .
例1: 如图,函数y=2x和y=- x+4的图象相交于点A.(1)求点A的坐标;(2)根据图象,直接写出不等式2x≥- x+4的解集.
解:(1)由 , 解得
∴点A的坐标为( ,3);
(2)由图象得不等式2x≥-3(2)x+4的解集为x≥2(3).
y=2x
y=- x+4
y=3
例2:一次函数y=kx+b(k≠0)中两个变量x、y的部分对应值如下表所示:
那么关于x的不等式kx+b≥-1的解集是________.
{5940675A-B579-460E-94D1-54222C63F5DA}x
…
-2
-1
0
1
2
…
y
…
8
5
2
-1
-4
…
x≤1
例3:如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( )
A.x>0B.0<x<1C.1<x<2D.x>2
C
四、巩固练习
1、若y1=-x+3,y2=3x-4,试确定当x取何值时
(1)y1<y2?
(2)y1=y2?
(3)y1>y2?
①解不等式法:
即:-x+3<3x-4
即:-x+3=3x-4
即:-x+3 < 3x-4
②函数图象法:
x
y
3
y1=-x+3
y2=3x-4
观察何时y1<y2
y1=y2
y1>y2
?
?
?
?
2.某单位准备和一个体车主或一国营出租车公司中的一家签订月租车合同,设汽车每月行驶x 千米,个体车主收费y1元,国营出租车公司收费为y2元,观察下列图象
可知,当x________时,选用个体车较合算.
3.当自变量 x 的取值满足什么条件时,函数 y = 3x+8 的值满足下列条件?
y = 0 (2) y = -7 (3) y >0 (4) y < 2
>1500
五、课堂小结
求ax+b>0(或<0)(a, b
是常数,a≠0)的解集
函数y= ax+b的函数值
大于0(或小于0)时x
的取值范围
直线y= ax+b在x轴上方或
下方时自变量的取值范围
从数的角度看
从形的角度看
求ax+b>0(或<0)(a, b
是常数,a≠0)的解集
“一次函数问题”可转换成 “一次不等式的问题” ;
反过来,
“一次不等式的问题”可转换成 “一次函数的问题”。
与一元一次不等式组
2.5 一元一次不等式与一次函数
第1课时 一元一次不等式与一次函数的关系
一、复习回顾
1.形如_______________形式,叫做一次函数;形如_______________形式,叫做正比例函数;确定一次函数图像需要_______个点。
2.一次函数的图象是__________.当kx+b_______0,表示直线在x轴上方的部分,当kx+b_______0,表示直线在x轴的交点,当kx+b_______0,表示直线在x轴下方的部分。
3. 一次函数 y = 2x – 5它与x轴的交点坐标是 ,与y轴的交点 坐标是 。
二、新课导入
小华准备将平时的零用钱储存起来,他已经存有300元,现在起每月存50元.小华的同学小丽以前没有存过零用钱,在听说小华存零用钱后,表示从现在起每月存70元,争取超过小华.根据以上信息,你能帮助小丽计算出她需要多久才能超过小华吗?
三、新课讲授
我们知道,一次函数的图象是一条直线。
作出一次函数 y = 2x - 5
的图象如右,
(2.5 , 0)
0
x
1
2
3
-1
4
1
-1
-2
3
-4
-3
2
-5
-6
y
观察图象回答下列问题:
x > 2.5 时
x = 2.5 时
x < 2.5 时
x > 4 时
(2.5 , 0)
0
x
1
2
3
-1
4
1
-1
-2
3
-4
-3
2
-5
-6
y
(1) x 取哪些值时, 2x-5=0 ?
(2) x 取哪些值时, 2x-5>0 ?
(3) x 取哪些值时, 2x-5<0 ?
(4) x 取哪些值时, 2x-5 >3 ?
求ax+b>0(或<0)(a, b
是常数,a≠0)的解集
函数y= ax+b的函数值
大于0(或小于0)时x
的取值范围
直线y= ax+b在x轴上方或
下方时自变量的取值范围
从数的角度看
从形的角度看
求ax+b>0(或<0)(a, b
是常数,a≠0)的解集
方法总结
如果 y=-2x-5 , 那么当 x 取何值时 , y>0 ?
你解答此道题, 可有几种方法 ?
用“函数图象法”及“解不等式法”解函数问题
法一:
将函数问题转化为不等式问题(从数的角度看)
即 解不等式
-2x- 5 > 0 ;
法二:
图象法(从形的角度看)
x
y
-1
-2
-3
-4
-5
1
-1
-2
-3
-4
-5
-6
1
2
3
由图易知,
当 x
< -2.5时 y>0 .
例1: 如图,函数y=2x和y=- x+4的图象相交于点A.(1)求点A的坐标;(2)根据图象,直接写出不等式2x≥- x+4的解集.
解:(1)由 , 解得
∴点A的坐标为( ,3);
(2)由图象得不等式2x≥-3(2)x+4的解集为x≥2(3).
y=2x
y=- x+4
y=3
例2:一次函数y=kx+b(k≠0)中两个变量x、y的部分对应值如下表所示:
那么关于x的不等式kx+b≥-1的解集是________.
{5940675A-B579-460E-94D1-54222C63F5DA}x
…
-2
-1
0
1
2
…
y
…
8
5
2
-1
-4
…
x≤1
例3:如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( )
A.x>0B.0<x<1C.1<x<2D.x>2
C
四、巩固练习
1、若y1=-x+3,y2=3x-4,试确定当x取何值时
(1)y1<y2?
(2)y1=y2?
(3)y1>y2?
①解不等式法:
即:-x+3<3x-4
即:-x+3=3x-4
即:-x+3 < 3x-4
②函数图象法:
x
y
3
y1=-x+3
y2=3x-4
观察何时y1<y2
y1=y2
y1>y2
?
?
?
?
2.某单位准备和一个体车主或一国营出租车公司中的一家签订月租车合同,设汽车每月行驶x 千米,个体车主收费y1元,国营出租车公司收费为y2元,观察下列图象
可知,当x________时,选用个体车较合算.
3.当自变量 x 的取值满足什么条件时,函数 y = 3x+8 的值满足下列条件?
y = 0 (2) y = -7 (3) y >0 (4) y < 2
>1500
五、课堂小结
求ax+b>0(或<0)(a, b
是常数,a≠0)的解集
函数y= ax+b的函数值
大于0(或小于0)时x
的取值范围
直线y= ax+b在x轴上方或
下方时自变量的取值范围
从数的角度看
从形的角度看
求ax+b>0(或<0)(a, b
是常数,a≠0)的解集
“一次函数问题”可转换成 “一次不等式的问题” ;
反过来,
“一次不等式的问题”可转换成 “一次函数的问题”。
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
