2.6.2一元一次不等式组的解法和应用-2020-2021学年北师大版八年级数学下册课件(共23张)
文档属性
| 名称 | 2.6.2一元一次不等式组的解法和应用-2020-2021学年北师大版八年级数学下册课件(共23张) |  | |
| 格式 | pptx | ||
| 文件大小 | 526.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-22 15:40:44 | ||
图片预览








文档简介
第二章 一元一次不等式
与一元一次不等式组
2.6 一元一次不等式组
第2课时 一元一次不等式组的解法及应用
一、复习回顾
解一元一次不等式组的解题步骤:
(1)求出不等式组中各个不等式的解集;
(2)利用数轴,找出这些不等式解集的公共部分;
(3)表示出这个不等式组的解集.
两个一元一次不等式所组成的不等式组的解集有以下四种情形.设a<b,那么(1)不等式组 的解集是x>b; 同大取大
(3)不等式组 的解集是a<x<b; 大小小大中间找
(4)不等式组 的解集是无解; 大大小小找不到
(2)不等式组 的解集是x<a; 同小取小
这是用式子表示,也可以用语言简单表述为:同大取大;同小取小;大小小大中间找;大大小小找不到。
1、解下列不等式组⑴
⑵
⑶
⑷
二、新课导入
思考:
1、在什么条件下,长度为3cm , 7cm , xcm的三条线段可以围成一个三角形?
2 、如何解不等式组3<2-3x<8
例1、解不等式组
②
①
三、新课讲授
解:解不等式①,得x>-1
解不等式② 得
在数轴上表示它们的解集:
-3
-2
-1
0
4
2
1
3
5
解一元一次不等式组的步骤:
求出这个不等式组中各个不等式的解集
借助数轴求出这些不等式的解集的公共部分,即求出了这个不等式组的解集
{5940675A-B579-460E-94D1-54222C63F5DA}不等式组
数轴表示
解集
填表:
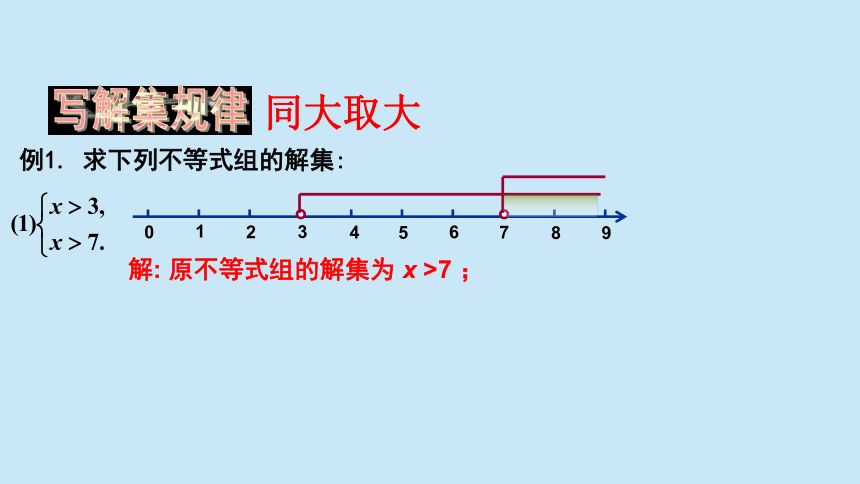
例1. 求下列不等式组的解集:
解: 原不等式组的解集为 x >7 ;
写解集规律
0
7
6
5
4
2
1
3
8
9
同大取大
解: 原不等式组的解集为 x >2 ;
-4
3
2
1
0
-2
-3
-1
4
5
解: 原不等式组的解集为 x >-2 ;
-6
1
0
-1
-2
-4
-5
-3
2
3
例1. 求下列不等式组的解集:
解: 原不等式组的解集为 x ≤3 ;
写解集规律
0
7
6
5
4
2
1
3
8
9
同小取小
解: 原不等式组的解集为 x ≤-5 ;
-7
0
-1
-2
-3
-5
-6
-4
1
2
解: 原不等式组的解集为 x<-1 ;
-3
4
3
2
1
-1
-2
0
5
6
例1. 求下列不等式组的解集:
解: 原不等式组的解集为 3 < x < 7 ;
写解集规律
0
7
6
5
4
2
1
3
8
9
大小、小大取中间
解: 原不等式组的解集为 -5< x <-2 ;
-8
-1
-2
-3
-4
-6
-7
-5
0
1
解: 原不等式组的解集为 -1≤x < 4 ;
-3
4
3
2
1
-1
-2
0
5
6
例1. 求下列不等式组的解集:
解: 原不等式组无解 ;
写解集规律
0
7
6
5
4
2
1
3
8
9
大大、小小解不了
-8
-1
-2
-3
-4
-6
-7
-5
0
1
-3
4
3
2
1
-1
-2
0
5
6
解: 原不等式组无解 ;
解: 原不等式组无解 ;
同大取大
的解集是
当a>b时,
x>a
x>b
x>a
同小取小
的解集是
当a>b时,
x<a
x<b
x<b
大小小大取中间
的解集是
当a>b时,
x<a
x≥b
b ≤ x<a
大小等同取等值
x=a
的解集是
x≥a
x≤a
不等式组
大大小小则无解
的解集是
当a>b时,
x > a
x < b
无解
文字记忆
数学语言
图形
4.解集及记忆方法
a
b
a
b
a
b
a
a
b
例2 解不等式组
例3 当x取哪些整数时,不等式2(x+2)<x+5与3(x-2)+8>2x同时成立?
例4 不等式组 的解集是x>a,则a的取值范围是 。
例5.某地区发生严重旱情,为了保障人畜饮水安全,急需饮水设备12台.现有甲、乙两种设备可供选择,其中甲种设备的购买费用为4000元/台,安装及运输费用为600元/台;乙种设备的购买费用为3000元/台,安装及运输费用为800元/台.若要求购买的费用不超过40000元,安装及运输费用不超过9200元,则可购买甲、乙两种设备各多少台?
解:设购买甲种设备x台,则购买乙种设备(12-x)台,购买设备的费用为4000x+3000(12-x),安装及运输费用为600x+800(12-x),根据题意得 600x+800(12-x)≤9200.
(4000x+3000(12-x)≤40000,)解得2≤x≤4,
由于x取整数,
所以x=2,3,4.答:有三种方案:①购买甲种设备2台,乙种设备10台;②购买甲种设备3台,乙种设备9台;③购买甲种设备4台,乙种设备8台.
四、巩固练习
1.解下列不等式组
2.若不等式组1-2x>x-2(x+a≥0,)无解,则实数a的取值范围是( )A.a≥-1 B.a<-1C.a≤1 D.a≤-1
3.求不等式组 的整数解.
五、课堂小结
1. 由几个一元一次不等式组所组成的不等式组
叫做一元一次不等式组
2. 几个一元一次不等式的解集的公共部分, 叫做由它们所组成的一元一次不等式组的解集.
3. 求不等式组的解集的过程, 叫做 解不等式组.
4. 解简单一元一次不等式组的方法:
(1) 利用数轴找几个解集的公共部分:
(2) 利用规律: 同大取大;
同小取小;
大小、小大取中间;
大大、小小解不了(是空集)。
与一元一次不等式组
2.6 一元一次不等式组
第2课时 一元一次不等式组的解法及应用
一、复习回顾
解一元一次不等式组的解题步骤:
(1)求出不等式组中各个不等式的解集;
(2)利用数轴,找出这些不等式解集的公共部分;
(3)表示出这个不等式组的解集.
两个一元一次不等式所组成的不等式组的解集有以下四种情形.设a<b,那么(1)不等式组 的解集是x>b; 同大取大
(3)不等式组 的解集是a<x<b; 大小小大中间找
(4)不等式组 的解集是无解; 大大小小找不到
(2)不等式组 的解集是x<a; 同小取小
这是用式子表示,也可以用语言简单表述为:同大取大;同小取小;大小小大中间找;大大小小找不到。
1、解下列不等式组⑴
⑵
⑶
⑷
二、新课导入
思考:
1、在什么条件下,长度为3cm , 7cm , xcm的三条线段可以围成一个三角形?
2 、如何解不等式组3<2-3x<8
例1、解不等式组
②
①
三、新课讲授
解:解不等式①,得x>-1
解不等式② 得
在数轴上表示它们的解集:
-3
-2
-1
0
4
2
1
3
5
解一元一次不等式组的步骤:
求出这个不等式组中各个不等式的解集
借助数轴求出这些不等式的解集的公共部分,即求出了这个不等式组的解集
{5940675A-B579-460E-94D1-54222C63F5DA}不等式组
数轴表示
解集
填表:
例1. 求下列不等式组的解集:
解: 原不等式组的解集为 x >7 ;
写解集规律
0
7
6
5
4
2
1
3
8
9
同大取大
解: 原不等式组的解集为 x >2 ;
-4
3
2
1
0
-2
-3
-1
4
5
解: 原不等式组的解集为 x >-2 ;
-6
1
0
-1
-2
-4
-5
-3
2
3
例1. 求下列不等式组的解集:
解: 原不等式组的解集为 x ≤3 ;
写解集规律
0
7
6
5
4
2
1
3
8
9
同小取小
解: 原不等式组的解集为 x ≤-5 ;
-7
0
-1
-2
-3
-5
-6
-4
1
2
解: 原不等式组的解集为 x<-1 ;
-3
4
3
2
1
-1
-2
0
5
6
例1. 求下列不等式组的解集:
解: 原不等式组的解集为 3 < x < 7 ;
写解集规律
0
7
6
5
4
2
1
3
8
9
大小、小大取中间
解: 原不等式组的解集为 -5< x <-2 ;
-8
-1
-2
-3
-4
-6
-7
-5
0
1
解: 原不等式组的解集为 -1≤x < 4 ;
-3
4
3
2
1
-1
-2
0
5
6
例1. 求下列不等式组的解集:
解: 原不等式组无解 ;
写解集规律
0
7
6
5
4
2
1
3
8
9
大大、小小解不了
-8
-1
-2
-3
-4
-6
-7
-5
0
1
-3
4
3
2
1
-1
-2
0
5
6
解: 原不等式组无解 ;
解: 原不等式组无解 ;
同大取大
的解集是
当a>b时,
x>a
x>b
x>a
同小取小
的解集是
当a>b时,
x<a
x<b
x<b
大小小大取中间
的解集是
当a>b时,
x<a
x≥b
b ≤ x<a
大小等同取等值
x=a
的解集是
x≥a
x≤a
不等式组
大大小小则无解
的解集是
当a>b时,
x > a
x < b
无解
文字记忆
数学语言
图形
4.解集及记忆方法
a
b
a
b
a
b
a
a
b
例2 解不等式组
例3 当x取哪些整数时,不等式2(x+2)<x+5与3(x-2)+8>2x同时成立?
例4 不等式组 的解集是x>a,则a的取值范围是 。
例5.某地区发生严重旱情,为了保障人畜饮水安全,急需饮水设备12台.现有甲、乙两种设备可供选择,其中甲种设备的购买费用为4000元/台,安装及运输费用为600元/台;乙种设备的购买费用为3000元/台,安装及运输费用为800元/台.若要求购买的费用不超过40000元,安装及运输费用不超过9200元,则可购买甲、乙两种设备各多少台?
解:设购买甲种设备x台,则购买乙种设备(12-x)台,购买设备的费用为4000x+3000(12-x),安装及运输费用为600x+800(12-x),根据题意得 600x+800(12-x)≤9200.
(4000x+3000(12-x)≤40000,)解得2≤x≤4,
由于x取整数,
所以x=2,3,4.答:有三种方案:①购买甲种设备2台,乙种设备10台;②购买甲种设备3台,乙种设备9台;③购买甲种设备4台,乙种设备8台.
四、巩固练习
1.解下列不等式组
2.若不等式组1-2x>x-2(x+a≥0,)无解,则实数a的取值范围是( )A.a≥-1 B.a<-1C.a≤1 D.a≤-1
3.求不等式组 的整数解.
五、课堂小结
1. 由几个一元一次不等式组所组成的不等式组
叫做一元一次不等式组
2. 几个一元一次不等式的解集的公共部分, 叫做由它们所组成的一元一次不等式组的解集.
3. 求不等式组的解集的过程, 叫做 解不等式组.
4. 解简单一元一次不等式组的方法:
(1) 利用数轴找几个解集的公共部分:
(2) 利用规律: 同大取大;
同小取小;
大小、小大取中间;
大大、小小解不了(是空集)。
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
