2020-2021学年 北师大版七年级数学下册 4.1 认识三角形 同步测试题(word版无答案)
文档属性
| 名称 | 2020-2021学年 北师大版七年级数学下册 4.1 认识三角形 同步测试题(word版无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 93.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-22 00:00:00 | ||
图片预览

文档简介
10312400103378004.1 认识三角形 同步测试题
班级:_____________姓名:_____________
一、 选择题 (本题共计 9 小题 ,每题 3 分 ,共计27分 , ) ?
1. 三角形的下列线段中一定能将三角形的面积分成相等的两部分的是(? ? ? ? )
A.中线 B.角平分线 C.高 D.中位线?
2. 适合条件∠A=∠B=∠C的三角形ABC是(??)
A.锐角三角形 B.直角三角形 C.钝角三角形 D.都有可能?
3. 关于三角形的三个内角,下面说法错误的是(? ? ? ? )
A.必有一内角不少于60? B.必有一内角不大于60?
C.最少有两个锐角 D.最多有两个锐角?
4. 已知,在Rt△ABC中,∠A=20?,则∠C的度数是( )
A.20? B.70? C.80? D.60??
5. 如果一个三角形的两条边长分别为2和6,那么这个三角形的周长可能是( )
A.10 B.11 C.12 D.14.2?
6. 已知a、b、c是三角形的三边长,化简:|a-b+c|-|a-b-c|=( )
A.2a-2b B.2a-2c C.a-2b D.0?
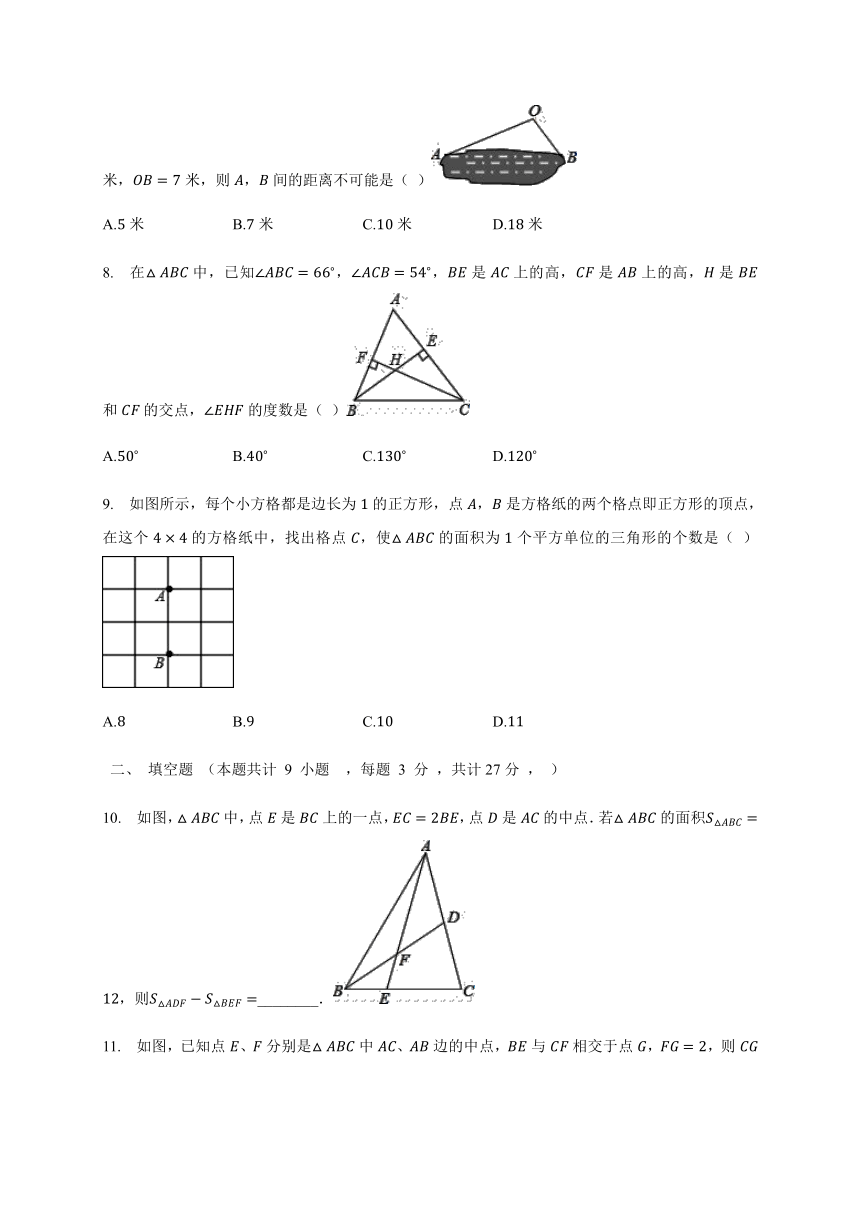
7. 如图,为了估计池塘岸边A,B两点间的距离,小玥同学在池塘一侧选取一点O,测得OA=12米,OB=7米,则A,B间的距离不可能是( )
A.5米 B.7米 C.10米 D.18米?
8. 在△ABC中,已知∠ABC=66?,∠ACB=54?,BE是AC上的高,CF是AB上的高,H是BE和CF的交点,∠EHF的度数是( )
A.50? B.40? C.130? D.120??
9. 如图所示,每个小方格都是边长为1的正方形,点A,B是方格纸的两个格点即正方形的顶点,在这个4×4的方格纸中,找出格点C,使△ABC的面积为1个平方单位的三角形的个数是( )
A.8 B.9 C.10 D.11
二、 填空题 (本题共计 9 小题 ,每题 3 分 ,共计27分 , ) ?
10. 如图,△ABC中,点E是BC上的一点,EC=2BE,点D是AC的中点.若△ABC的面积S△ABC=12,则S△ADF-S△BEF=________. ?
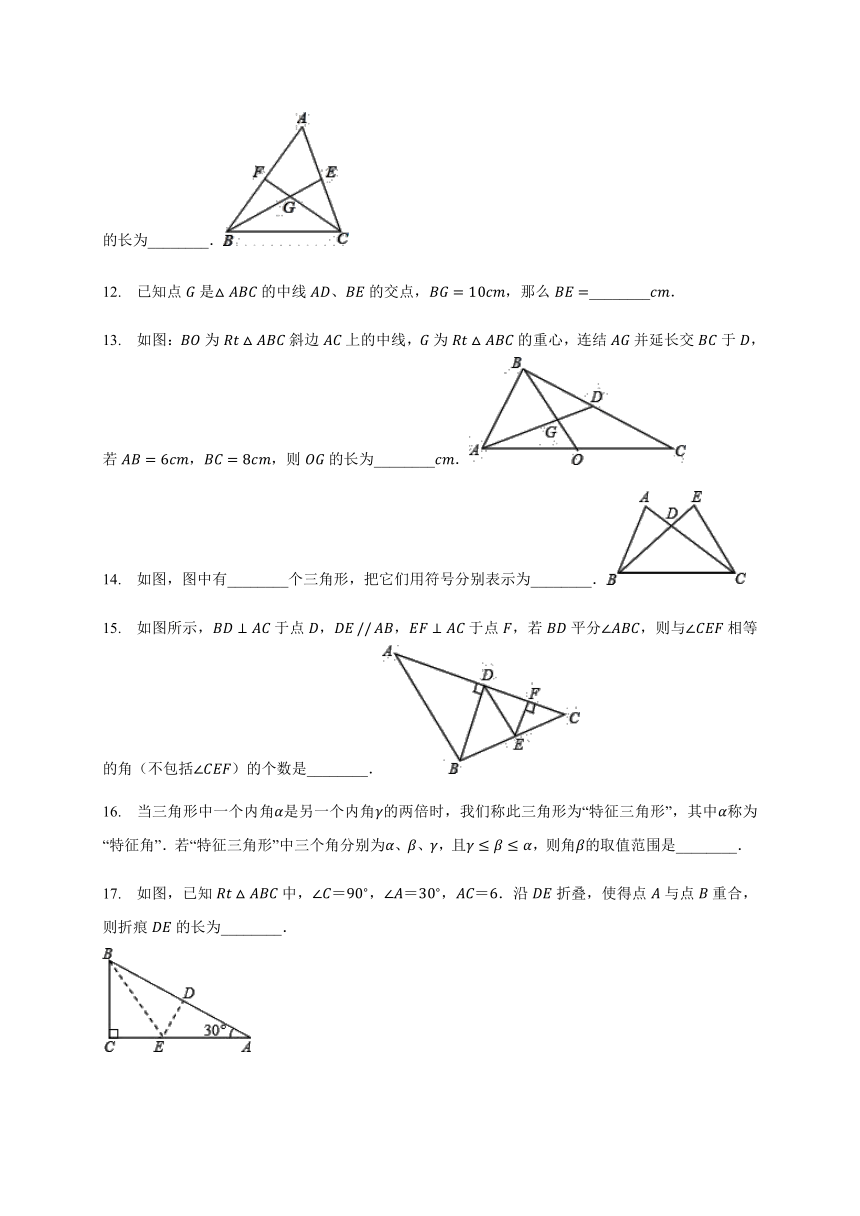
11. 如图,已知点E、F分别是△ABC中AC、AB边的中点,BE与CF相交于点G,FG=2,则CG的长为________. ?
12. 已知点G是△ABC的中线AD、BE的交点,BG=10cm,那么BE=________cm. ?
13. 如图:BO为Rt△ABC斜边AC上的中线,G为Rt△ABC的重心,连结AG并延长交BC于D,若AB=6cm,BC=8cm,则OG的长为________cm. ?
14. 如图,图中有________个三角形,把它们用符号分别表示为________. ?
15. 如图所示,BD⊥AC于点D,DE?//?AB,EF⊥AC于点F,若BD平分∠ABC,则与∠CEF相等的角(不包括∠CEF)的个数是________. ?
16. 当三角形中一个内角α是另一个内角γ的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.若“特征三角形”中三个角分别为α、β、γ,且γ≤β≤α,则角β的取值范围是________. ?
17. 如图,已知Rt△ABC中,∠C=90?,∠A=30?,AC=6.沿DE折叠,使得点A与点B重合,则折痕DE的长为________.
?
18. 小华在电话中问小明:“已知一个三角形三边长分别是4,9,12,如何求这个三角形的面积?小明提示说:“可通过作最长边上的高来求解.”小华根据小明的提示作出的图形正确的是________
三、 解答题 (本题共计 7 小题 ,共计66分 , )
19. 如图,在△ABC中,BE⊥AC,BC=5cm,AC=8cm,BE=3cm,
(1)求△ABC的面积;?
(2)画出△ABC中的BC边上的高AD,并求出AD的值.
?
20. 如图,在△ABC中,BD、CE是边AC、AB上的中线,BD与CE相交于点O,N是OC的中点.
(1)求证:OC=2OE;
(2)若S△CDN=1,求△ABC的面积.
?
21. 如图所示,在△ABC中,AD、BE相交于点O,BD:CD=3:2,AE:CE=2:1,若S△COD=2,求:
(1)S△BOC:S△AOC:S△AOB的值.
(2)求S△ABC.
?
22. 如图,已知:方格纸中的每个小方格是边长为1的正方形,A、B两点在小方格的顶点上确定一点,连接AB、AC、BC,使△ABC的面积为2个平方单位.
?
23. 如图,BD是△ABC的中线,点P是△ABC的重心,连接PC.
(1)写出图中的所有三角形________;
(2)若延长CP交AB于点E,BC=5cm,AC=7cm,AB为整数,求整数AE的长.
?
24. 已知a,b,c为三角形的三边.
(1)判断:a+b-c________0;(用不等号“<”或“>”表示)
(2)说明:a2-b2-c2-2bc<0.
?
25. 如图,BO、CO分别平分∠ABC和∠ACB,
(1)若∠A=60?时,则∠O=________度
(2)若∠A=100?时,则∠O=________度
(3)由(1)、(2)你发现了什么规律?当∠A的度数发生变化后,你的结论仍成立吗?(提示:三解形的内角和等于180?)
班级:_____________姓名:_____________
一、 选择题 (本题共计 9 小题 ,每题 3 分 ,共计27分 , ) ?
1. 三角形的下列线段中一定能将三角形的面积分成相等的两部分的是(? ? ? ? )
A.中线 B.角平分线 C.高 D.中位线?
2. 适合条件∠A=∠B=∠C的三角形ABC是(??)
A.锐角三角形 B.直角三角形 C.钝角三角形 D.都有可能?
3. 关于三角形的三个内角,下面说法错误的是(? ? ? ? )
A.必有一内角不少于60? B.必有一内角不大于60?
C.最少有两个锐角 D.最多有两个锐角?
4. 已知,在Rt△ABC中,∠A=20?,则∠C的度数是( )
A.20? B.70? C.80? D.60??
5. 如果一个三角形的两条边长分别为2和6,那么这个三角形的周长可能是( )
A.10 B.11 C.12 D.14.2?
6. 已知a、b、c是三角形的三边长,化简:|a-b+c|-|a-b-c|=( )
A.2a-2b B.2a-2c C.a-2b D.0?
7. 如图,为了估计池塘岸边A,B两点间的距离,小玥同学在池塘一侧选取一点O,测得OA=12米,OB=7米,则A,B间的距离不可能是( )
A.5米 B.7米 C.10米 D.18米?
8. 在△ABC中,已知∠ABC=66?,∠ACB=54?,BE是AC上的高,CF是AB上的高,H是BE和CF的交点,∠EHF的度数是( )
A.50? B.40? C.130? D.120??
9. 如图所示,每个小方格都是边长为1的正方形,点A,B是方格纸的两个格点即正方形的顶点,在这个4×4的方格纸中,找出格点C,使△ABC的面积为1个平方单位的三角形的个数是( )
A.8 B.9 C.10 D.11
二、 填空题 (本题共计 9 小题 ,每题 3 分 ,共计27分 , ) ?
10. 如图,△ABC中,点E是BC上的一点,EC=2BE,点D是AC的中点.若△ABC的面积S△ABC=12,则S△ADF-S△BEF=________. ?
11. 如图,已知点E、F分别是△ABC中AC、AB边的中点,BE与CF相交于点G,FG=2,则CG的长为________. ?
12. 已知点G是△ABC的中线AD、BE的交点,BG=10cm,那么BE=________cm. ?
13. 如图:BO为Rt△ABC斜边AC上的中线,G为Rt△ABC的重心,连结AG并延长交BC于D,若AB=6cm,BC=8cm,则OG的长为________cm. ?
14. 如图,图中有________个三角形,把它们用符号分别表示为________. ?
15. 如图所示,BD⊥AC于点D,DE?//?AB,EF⊥AC于点F,若BD平分∠ABC,则与∠CEF相等的角(不包括∠CEF)的个数是________. ?
16. 当三角形中一个内角α是另一个内角γ的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.若“特征三角形”中三个角分别为α、β、γ,且γ≤β≤α,则角β的取值范围是________. ?
17. 如图,已知Rt△ABC中,∠C=90?,∠A=30?,AC=6.沿DE折叠,使得点A与点B重合,则折痕DE的长为________.
?
18. 小华在电话中问小明:“已知一个三角形三边长分别是4,9,12,如何求这个三角形的面积?小明提示说:“可通过作最长边上的高来求解.”小华根据小明的提示作出的图形正确的是________
三、 解答题 (本题共计 7 小题 ,共计66分 , )
19. 如图,在△ABC中,BE⊥AC,BC=5cm,AC=8cm,BE=3cm,
(1)求△ABC的面积;?
(2)画出△ABC中的BC边上的高AD,并求出AD的值.
?
20. 如图,在△ABC中,BD、CE是边AC、AB上的中线,BD与CE相交于点O,N是OC的中点.
(1)求证:OC=2OE;
(2)若S△CDN=1,求△ABC的面积.
?
21. 如图所示,在△ABC中,AD、BE相交于点O,BD:CD=3:2,AE:CE=2:1,若S△COD=2,求:
(1)S△BOC:S△AOC:S△AOB的值.
(2)求S△ABC.
?
22. 如图,已知:方格纸中的每个小方格是边长为1的正方形,A、B两点在小方格的顶点上确定一点,连接AB、AC、BC,使△ABC的面积为2个平方单位.
?
23. 如图,BD是△ABC的中线,点P是△ABC的重心,连接PC.
(1)写出图中的所有三角形________;
(2)若延长CP交AB于点E,BC=5cm,AC=7cm,AB为整数,求整数AE的长.
?
24. 已知a,b,c为三角形的三边.
(1)判断:a+b-c________0;(用不等号“<”或“>”表示)
(2)说明:a2-b2-c2-2bc<0.
?
25. 如图,BO、CO分别平分∠ABC和∠ACB,
(1)若∠A=60?时,则∠O=________度
(2)若∠A=100?时,则∠O=________度
(3)由(1)、(2)你发现了什么规律?当∠A的度数发生变化后,你的结论仍成立吗?(提示:三解形的内角和等于180?)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
