6.1.2 两个计数原理的综合应用(习题课)-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册课件(14张 ppt )
文档属性
| 名称 | 6.1.2 两个计数原理的综合应用(习题课)-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册课件(14张 ppt ) |

|
|
| 格式 | pptx | ||
| 文件大小 | 348.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 00:00:00 | ||
图片预览





文档简介
两个计数原理
——综合应用(习题课)
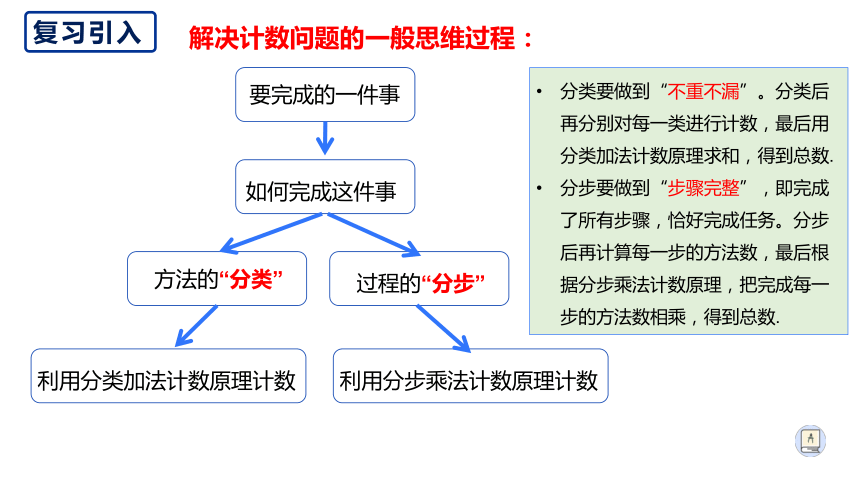
解决计数问题的一般思维过程:
要完成的一件事
如何完成这件事
方法的“分类”
过程的“分步”
利用分类加法计数原理计数
利用分步乘法计数原理计数
分类要做到“不重不漏”。分类后再分别对每一类进行计数,最后用分类加法计数原理求和,得到总数.
分步要做到“步骤完整”,即完成了所有步骤,恰好完成任务。分步后再计算每一步的方法数,最后根据分步乘法计数原理,把完成每一步的方法数相乘,得到总数.
复习引入
题型一:分类加法计数原理和分步乘法计数原理的直接应用
1.从5名同学中选出正、副组长各1名,有多少种不同的选法?
解:要完成的一件事是“从5名同学中选出正、副组长各1名”,分两步完成:第1步,选正组长,有5种方法;第2步,选副组长,有4种方法,所以共有5×4=20种。
2.在1,2,…,500中,被5除余2的数共有多少个?
法一:解:被5除余2的数的末位是2或7,在1,2,…,500中符合题意的数分为3类:
第1类:一位数,只有2,7两个数;.
第2类:两位数,个位数有2,7两种取法,十位数有9种取法,共有2×9=18个数;
第3类:三位数,个位数有2,7两种取法,十位数有10种取法,百位数可以为1,2,3,4,共4种取法,共有2×10×4=80个数。
所以,N=2+18+80=100.
题型一:分类加法计数原理和分步乘法计数原理的直接应用
1.从5名同学中选出正、副组长各1名,有多少种不同的选法?
解:要完成的一件事是“从5名同学中选出正、副组长各1名”,分两步完成:第1步,选正组长,有5种方法;第2步,选副组长,有4种方法,所以共有5×4=20种。
2.在1,2,…,500中,被5除余2的数共有多少个?
法二:
5=k ...2
=
5k +2
=
所以,N=100.
题型一:分类加法计数原理和分步乘法计数原理的直接应用
变式1:各位上的数字不可以重复?
变式2:0.1.2.3.4 可以组成多少个三位数?(各位上的数字不可以重复)
3.由数字1,2,3,4,5可以组成多少个三位数(各位上的数字可以重复)?
解:分3步来解决,由于各位上的数字可重复,因此三位数中每一位都有5种来法,所以共可以组成5×5×5=125个三位数.
解:分3步来解决,由于各位上的数字不可重复,
第1步:选一个百位数字,5种;第2步:选一个十位数字,4种;第3步:选一个个位数字,3种
所以共可以组成5×4×3=60个三位数.
解:分3步来解决,由于各位上的数字不可重复,
第1步:选一个百位数字,在1,2,3,4四个数里选一个,4种选择;第2步:选一个十位数字,4种;第3步:选一个个位数字,3种;所以共可以组成4×4×3=48个三位数.
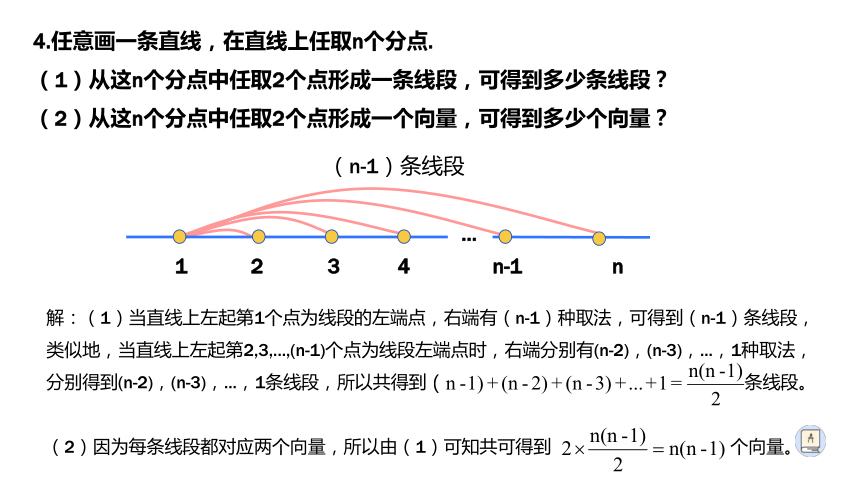
4.任意画一条直线,在直线上任取n个分点.
(1)从这n个分点中任取2个点形成一条线段,可得到多少条线段?
(2)从这n个分点中任取2个点形成一个向量,可得到多少个向量?
解:(1)当直线上左起第1个点为线段的左端点,右端有(n-1)种取法,可得到(n-1)条线段,类似地,当直线上左起第2,3,...,(n-1)个点为线段左端点时,右端分别有(n-2),(n-3),...,1种取法,分别得到(n-2),(n-3),...,1条线段,所以共得到 条线段。
(2)因为每条线段都对应两个向量,所以由(1)可知共可得到 个向量。
...
1
2
3
n-1
4
n
(n-1)条线段
题型二:投信问题
例1. 把3封信投到4个信箱,所有可能的投法有多少种?
练习1:(课本12页 8题)
(1)4名同学分别报名参加学校的足球队、篮球队、乒乓球队,每人限报其中的一个运动队,不同报法的种数是34还是43?
(2)3个班分别从5个景点中选择一处游览,不同选法的种数是35还是53?
易错点:分不清两个计数原理,首先明确“要完成的一件事”,如何完成?分类还是分步,然后合理选择计数原理。
解:(1)一件事情是“4名同学分别参加3个运动队中的一个,每人限报一个,可以报同一个运动队”,应该是人选运动队,所以不同报法种数是34.
(2)一件事情是“3个班分别从5个景点中选择一处游览”,应该是班选景点,故不同的选法种数是53.
题型三:涂色类问题
例2.将红、黄、蓝、白、黑五种颜色涂在如图所示“田”字形的4个小方格内,每格涂一种颜色,相邻两格涂不同的颜色,如果颜色可以反复使用,共有多少种不同的涂色方法?
解:第1个小方格可以从五种颜色中任取一种颜色涂上,有5种不同的涂法.
①当第2个、第3个小方格涂不同颜色时,有4×3=12(种)不同的涂法,第4个小方格有3种不同的涂法,由分步乘法计数原理可知有5×12×3=180(种)不同的涂法.
②当第2个、第3个小方格涂相同颜色时,有4种涂法,由于相邻两格不同色,因此,第4个小方格也有4种不同的涂法,由分步乘法计数原理可知有5×4×4=80(种)不同的涂法.
由分类加法计数原理可得共有180+80=260(种)不同的涂法.
题型三:涂色类问题
练习1:本例中的区域改为如图所示,其他条件均不变,则不同的涂法共有多少种?
将红、黄、蓝、白、黑五种颜色涂在如图所示“田”字形的4个小方格内,每格涂一种颜色,相邻两格涂不同的颜色,如果颜色可以反复使用,共有多少种不同的涂色方法?
法一:依题意,可分两类:①④不同色;①④同色.
第1类,①④不同色,则①②③④所涂的颜色各不相同,我们可将这件事情分成四步来完成.
第1步涂①,从5种颜色中任选一种,有5种涂法;第2步涂②,从余下的4种颜色中任选一种,有4种涂法;第3步涂③与第4步涂④时,分别有3种涂法和2种涂法.
于是由分步乘法计数原理得,不同的涂法为5×4×3×2=120(种).
第2类,①④同色,则①②③不同色,我们可将涂色工作分成三步来完成.
第1步涂①④,有5种涂法;第2步涂②,有4种涂法;第3步涂③,有3种涂法.
于是由分步乘法计数原理得,不同的涂法有5×4×3=60(种).
综上可知,所求的涂色方法共有120+60=180(种).
题型三:涂色类问题
练习1:本例中的区域改为如图所示,其他条件均不变,则不同的涂法共有多少种?
将红、黄、蓝、白、黑五种颜色涂在如图所示“田”字形的4个小方格内,每格涂一种颜色,相邻两格涂不同的颜色,如果颜色可以反复使用,共有多少种不同的涂色方法?
法二:
第1步涂②,从5种颜色中任选一种,有5种涂法;
第2步涂③,从余下的4种颜色中任选一种,有4种涂法;
第3步涂①,与第4步涂④时,分别有3种涂法.
于是由分步乘法计数原理得,不同的涂法有5×4×3×3=180(种).
先涂相邻最多的方格。
题型三:涂色类问题
练习2:(课本12页 11题)
在国庆长假期间,要从7人中选若干人在7天假期值班(每天只需1人值班),不出现同一人;连续值班2天,有多少种可能的安排方法?
解:利用分步乘法计数原理,分七步来求解。
第一步,安排第一天的值班人员,有7种方法;
第二步,安排第二天的值班人员,有6种方法;除第一天值班的人外,剩余6人都可安排。
第三步,安排第三天的值班人员,有6种方法;除第二天值班的人外(包括第一天值班的人),剩余6人都可安排。
同理,第四、五、六、七步均有6种方法。
公上所述,共有7×6×6×6×6×6×6=26592.
题型三:涂色类问题
练习3:(课本27页 17题)
如图,现要用5种不同的颜色对某市的4个区县地图进行着色,要求有公共边的两个地区不能用同一种颜色,共有几种不同的着色方法?
解:可以按照Ⅰ、Ⅱ、Ⅲ、Ⅳ的顺序着色,所以不同的着色方法种数为 5?4?3?3=180
课堂小结
题型一:分类加法计数原理和分步乘法计数原理的直接应用;
题型二:投信问题;
题型三:涂色类问题;
——综合应用(习题课)
解决计数问题的一般思维过程:
要完成的一件事
如何完成这件事
方法的“分类”
过程的“分步”
利用分类加法计数原理计数
利用分步乘法计数原理计数
分类要做到“不重不漏”。分类后再分别对每一类进行计数,最后用分类加法计数原理求和,得到总数.
分步要做到“步骤完整”,即完成了所有步骤,恰好完成任务。分步后再计算每一步的方法数,最后根据分步乘法计数原理,把完成每一步的方法数相乘,得到总数.
复习引入
题型一:分类加法计数原理和分步乘法计数原理的直接应用
1.从5名同学中选出正、副组长各1名,有多少种不同的选法?
解:要完成的一件事是“从5名同学中选出正、副组长各1名”,分两步完成:第1步,选正组长,有5种方法;第2步,选副组长,有4种方法,所以共有5×4=20种。
2.在1,2,…,500中,被5除余2的数共有多少个?
法一:解:被5除余2的数的末位是2或7,在1,2,…,500中符合题意的数分为3类:
第1类:一位数,只有2,7两个数;.
第2类:两位数,个位数有2,7两种取法,十位数有9种取法,共有2×9=18个数;
第3类:三位数,个位数有2,7两种取法,十位数有10种取法,百位数可以为1,2,3,4,共4种取法,共有2×10×4=80个数。
所以,N=2+18+80=100.
题型一:分类加法计数原理和分步乘法计数原理的直接应用
1.从5名同学中选出正、副组长各1名,有多少种不同的选法?
解:要完成的一件事是“从5名同学中选出正、副组长各1名”,分两步完成:第1步,选正组长,有5种方法;第2步,选副组长,有4种方法,所以共有5×4=20种。
2.在1,2,…,500中,被5除余2的数共有多少个?
法二:
5=k ...2
=
5k +2
=
所以,N=100.
题型一:分类加法计数原理和分步乘法计数原理的直接应用
变式1:各位上的数字不可以重复?
变式2:0.1.2.3.4 可以组成多少个三位数?(各位上的数字不可以重复)
3.由数字1,2,3,4,5可以组成多少个三位数(各位上的数字可以重复)?
解:分3步来解决,由于各位上的数字可重复,因此三位数中每一位都有5种来法,所以共可以组成5×5×5=125个三位数.
解:分3步来解决,由于各位上的数字不可重复,
第1步:选一个百位数字,5种;第2步:选一个十位数字,4种;第3步:选一个个位数字,3种
所以共可以组成5×4×3=60个三位数.
解:分3步来解决,由于各位上的数字不可重复,
第1步:选一个百位数字,在1,2,3,4四个数里选一个,4种选择;第2步:选一个十位数字,4种;第3步:选一个个位数字,3种;所以共可以组成4×4×3=48个三位数.
4.任意画一条直线,在直线上任取n个分点.
(1)从这n个分点中任取2个点形成一条线段,可得到多少条线段?
(2)从这n个分点中任取2个点形成一个向量,可得到多少个向量?
解:(1)当直线上左起第1个点为线段的左端点,右端有(n-1)种取法,可得到(n-1)条线段,类似地,当直线上左起第2,3,...,(n-1)个点为线段左端点时,右端分别有(n-2),(n-3),...,1种取法,分别得到(n-2),(n-3),...,1条线段,所以共得到 条线段。
(2)因为每条线段都对应两个向量,所以由(1)可知共可得到 个向量。
...
1
2
3
n-1
4
n
(n-1)条线段
题型二:投信问题
例1. 把3封信投到4个信箱,所有可能的投法有多少种?
练习1:(课本12页 8题)
(1)4名同学分别报名参加学校的足球队、篮球队、乒乓球队,每人限报其中的一个运动队,不同报法的种数是34还是43?
(2)3个班分别从5个景点中选择一处游览,不同选法的种数是35还是53?
易错点:分不清两个计数原理,首先明确“要完成的一件事”,如何完成?分类还是分步,然后合理选择计数原理。
解:(1)一件事情是“4名同学分别参加3个运动队中的一个,每人限报一个,可以报同一个运动队”,应该是人选运动队,所以不同报法种数是34.
(2)一件事情是“3个班分别从5个景点中选择一处游览”,应该是班选景点,故不同的选法种数是53.
题型三:涂色类问题
例2.将红、黄、蓝、白、黑五种颜色涂在如图所示“田”字形的4个小方格内,每格涂一种颜色,相邻两格涂不同的颜色,如果颜色可以反复使用,共有多少种不同的涂色方法?
解:第1个小方格可以从五种颜色中任取一种颜色涂上,有5种不同的涂法.
①当第2个、第3个小方格涂不同颜色时,有4×3=12(种)不同的涂法,第4个小方格有3种不同的涂法,由分步乘法计数原理可知有5×12×3=180(种)不同的涂法.
②当第2个、第3个小方格涂相同颜色时,有4种涂法,由于相邻两格不同色,因此,第4个小方格也有4种不同的涂法,由分步乘法计数原理可知有5×4×4=80(种)不同的涂法.
由分类加法计数原理可得共有180+80=260(种)不同的涂法.
题型三:涂色类问题
练习1:本例中的区域改为如图所示,其他条件均不变,则不同的涂法共有多少种?
将红、黄、蓝、白、黑五种颜色涂在如图所示“田”字形的4个小方格内,每格涂一种颜色,相邻两格涂不同的颜色,如果颜色可以反复使用,共有多少种不同的涂色方法?
法一:依题意,可分两类:①④不同色;①④同色.
第1类,①④不同色,则①②③④所涂的颜色各不相同,我们可将这件事情分成四步来完成.
第1步涂①,从5种颜色中任选一种,有5种涂法;第2步涂②,从余下的4种颜色中任选一种,有4种涂法;第3步涂③与第4步涂④时,分别有3种涂法和2种涂法.
于是由分步乘法计数原理得,不同的涂法为5×4×3×2=120(种).
第2类,①④同色,则①②③不同色,我们可将涂色工作分成三步来完成.
第1步涂①④,有5种涂法;第2步涂②,有4种涂法;第3步涂③,有3种涂法.
于是由分步乘法计数原理得,不同的涂法有5×4×3=60(种).
综上可知,所求的涂色方法共有120+60=180(种).
题型三:涂色类问题
练习1:本例中的区域改为如图所示,其他条件均不变,则不同的涂法共有多少种?
将红、黄、蓝、白、黑五种颜色涂在如图所示“田”字形的4个小方格内,每格涂一种颜色,相邻两格涂不同的颜色,如果颜色可以反复使用,共有多少种不同的涂色方法?
法二:
第1步涂②,从5种颜色中任选一种,有5种涂法;
第2步涂③,从余下的4种颜色中任选一种,有4种涂法;
第3步涂①,与第4步涂④时,分别有3种涂法.
于是由分步乘法计数原理得,不同的涂法有5×4×3×3=180(种).
先涂相邻最多的方格。
题型三:涂色类问题
练习2:(课本12页 11题)
在国庆长假期间,要从7人中选若干人在7天假期值班(每天只需1人值班),不出现同一人;连续值班2天,有多少种可能的安排方法?
解:利用分步乘法计数原理,分七步来求解。
第一步,安排第一天的值班人员,有7种方法;
第二步,安排第二天的值班人员,有6种方法;除第一天值班的人外,剩余6人都可安排。
第三步,安排第三天的值班人员,有6种方法;除第二天值班的人外(包括第一天值班的人),剩余6人都可安排。
同理,第四、五、六、七步均有6种方法。
公上所述,共有7×6×6×6×6×6×6=26592.
题型三:涂色类问题
练习3:(课本27页 17题)
如图,现要用5种不同的颜色对某市的4个区县地图进行着色,要求有公共边的两个地区不能用同一种颜色,共有几种不同的着色方法?
解:可以按照Ⅰ、Ⅱ、Ⅲ、Ⅳ的顺序着色,所以不同的着色方法种数为 5?4?3?3=180
课堂小结
题型一:分类加法计数原理和分步乘法计数原理的直接应用;
题型二:投信问题;
题型三:涂色类问题;
