5.3.2 函数的极值与最大(小)值(2)-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第二册课件(13张PPT)
文档属性
| 名称 | 5.3.2 函数的极值与最大(小)值(2)-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第二册课件(13张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 273.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 21:21:59 | ||
图片预览




文档简介
5.3.2 函数的极值
与最大(小)值(二)
1.了解函数最大(小)值的概念以及与函数极值的区别与联系;2.初步掌握求函数最值的方法;3.体会数形结合、化归转化的数学思想.
复习引入
如果在x0附近的左侧f '(x)>0,右侧f '(x)<0 ,那么 f (x0) 为极大值;
解方程 f '(x) = 0.当 f '(x0) = 0 时:
如果在x0附近的左侧f '(x)<0,右侧f '(x)>0 ,那么 f (x0) 为极小值;
1.求函数 y=f(x)的极值的一般方法:
2.函数最大值和最小值的概念:
一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:
(1)对于任意的x∈I,都有f(x)≤M; (2)存在x0∈I,使得f(x0) = M
那么,称M是函数y=f(x)的最大值;
一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:
(2)对于任意的x∈I,都有f(x)≥M; (2)存在x0∈I,使得f(x0) = M
那么,称M是函数y=f(x)的最小值 。
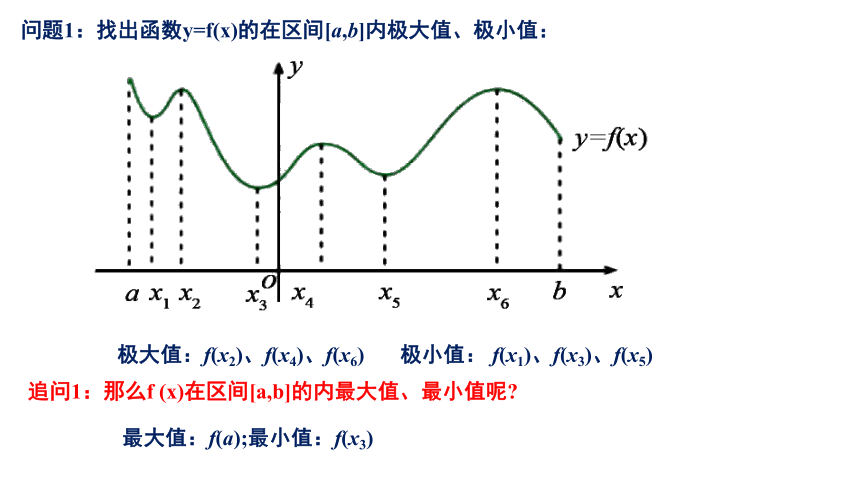
问题1:找出函数y=f(x)的在区间[a,b]内极大值、极小值:
追问1:那么f (x)在区间[a,b]的内最大值、最小值呢?
极大值:f(x2)、f(x4)、f(x6)
极小值: f(x1)、f(x3)、f(x5)
最大值:f(a);最小值:f(x3)
x
y
O
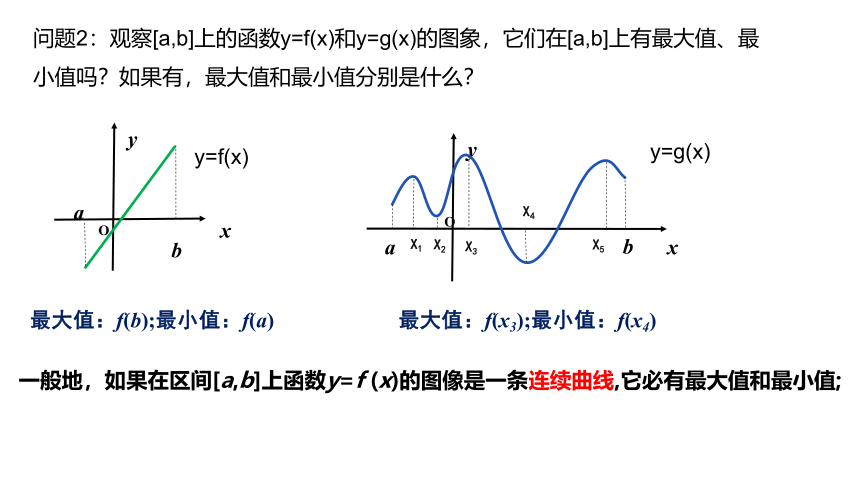
问题2:观察[a,b]上的函数y=f(x)和y=g(x)的图象,它们在[a,b]上有最大值、最小值吗?如果有,最大值和最小值分别是什么?
a
b
y=f(x)
x
y
O
a
b
X2
X1
X3
X4
X5
y=g(x)
最大值:f(b);最小值:f(a)
最大值:f(x3);最小值:f(x4)
一般地,如果在区间[a,b]上函数y=f (x)的图像是一条连续曲线,它必有最大值和最小值;
追问1:函数最值与极值有什么关系?
联系:只要把函数y=f(x)的所有极值连同端点的函数值进行比较,就可以求出函数的最大值和最小值。
区别:
1、函数的最大值、最小值是比较整个定义域上的函数值得出的,函数的极大值、极小值是比较极值点附近的函数值得出的。
2、函数的极值可以有多个,但函数在其定义域上的最大值、最小值最多各有一个。
3、极值只能在区间内取得,最值则可以在端点处取得;有最值未必有极值;极值有可能成为最值,最值只要不在端点处取得必定是极值。
追问2:为什么给定函数的区间必须是闭区间?
因为不能保证f(x)在开区间上有最大值和最小值(最值有可能在区间端点处取得)。
解:因为
x
(0,2)
2
(2,3)
y′
y
令 , 解得x1=-2 , x2=2.
单调递减
-4/3
+
-
0
所以,当x=0时,函数f(x)在[0,3]上取得最大值4,
当x=2时,函数f(x)在[0,3]上取得最小值- 4/3.
例1:求
在[0,3]的最大值与最小值;
又因为f(0)=4,f(3)=1
单调递增
求f(x)在[a,b]上的最大值与最小值的步骤如下:
(1)f(x)在(a,b)内导函数为零的点,并计算出其函数值;
(2)将f(x)的各导数值为零的点的函数值与f(a)、f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
解:(1)因为
x
y′
y
令 解得x= .
单调递减
+
-
0
所以,当x=2时,函数f(x)在[0,3]上取得最大值20,
当x= 时,函数f(x)在[0,3]上取得最小值 .
练习1:求下列函数在给定区间上的最大值与最小值;
又因为f(0)=-2,f(2)=20
单调递增
解:(2)因为
x
y′
y
令 解得 .
单调递减
+
-
0
所以,当x=2时,函数f(x)在 上取得最大值22,
当x= 时,函数f(x)在 上取得最小值 .
练习1:求下列函数在给定区间上的最大值与最小值;
又因为
单调递增
课堂小结
1.最大(小)值的概念
一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:
(1)对于任意的x∈I,都有f(x)≤M; (2)存在x0∈I,使得f(x0) = M
那么,称M是函数y=f(x)的最大值;
设函数y=f(x)的定义域为I,如果存在实数M满足:
(2)对于任意的x∈I,都有f(x)≥M; (2)存在x0∈I,使得f(x0) = M
那么,称M是函数y=f(x)的最小值 。
2.最大(小)值与函数极值的区别与联系
只要把函数y=f(x)的所有极值连同端点的函数值进行比较,就可以求出函数的最大值和最小值。
课堂小结
3.求f(x)在[a,b]上的最大值与最小值的步骤如下:
(1)f(x)在(a,b)内导函数为零的点,并计算出其函数值;
(2)将f(x)的各导数值为零的点的函数值与f(a)、f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
与最大(小)值(二)
1.了解函数最大(小)值的概念以及与函数极值的区别与联系;2.初步掌握求函数最值的方法;3.体会数形结合、化归转化的数学思想.
复习引入
如果在x0附近的左侧f '(x)>0,右侧f '(x)<0 ,那么 f (x0) 为极大值;
解方程 f '(x) = 0.当 f '(x0) = 0 时:
如果在x0附近的左侧f '(x)<0,右侧f '(x)>0 ,那么 f (x0) 为极小值;
1.求函数 y=f(x)的极值的一般方法:
2.函数最大值和最小值的概念:
一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:
(1)对于任意的x∈I,都有f(x)≤M; (2)存在x0∈I,使得f(x0) = M
那么,称M是函数y=f(x)的最大值;
一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:
(2)对于任意的x∈I,都有f(x)≥M; (2)存在x0∈I,使得f(x0) = M
那么,称M是函数y=f(x)的最小值 。
问题1:找出函数y=f(x)的在区间[a,b]内极大值、极小值:
追问1:那么f (x)在区间[a,b]的内最大值、最小值呢?
极大值:f(x2)、f(x4)、f(x6)
极小值: f(x1)、f(x3)、f(x5)
最大值:f(a);最小值:f(x3)
x
y
O
问题2:观察[a,b]上的函数y=f(x)和y=g(x)的图象,它们在[a,b]上有最大值、最小值吗?如果有,最大值和最小值分别是什么?
a
b
y=f(x)
x
y
O
a
b
X2
X1
X3
X4
X5
y=g(x)
最大值:f(b);最小值:f(a)
最大值:f(x3);最小值:f(x4)
一般地,如果在区间[a,b]上函数y=f (x)的图像是一条连续曲线,它必有最大值和最小值;
追问1:函数最值与极值有什么关系?
联系:只要把函数y=f(x)的所有极值连同端点的函数值进行比较,就可以求出函数的最大值和最小值。
区别:
1、函数的最大值、最小值是比较整个定义域上的函数值得出的,函数的极大值、极小值是比较极值点附近的函数值得出的。
2、函数的极值可以有多个,但函数在其定义域上的最大值、最小值最多各有一个。
3、极值只能在区间内取得,最值则可以在端点处取得;有最值未必有极值;极值有可能成为最值,最值只要不在端点处取得必定是极值。
追问2:为什么给定函数的区间必须是闭区间?
因为不能保证f(x)在开区间上有最大值和最小值(最值有可能在区间端点处取得)。
解:因为
x
(0,2)
2
(2,3)
y′
y
令 , 解得x1=-2 , x2=2.
单调递减
-4/3
+
-
0
所以,当x=0时,函数f(x)在[0,3]上取得最大值4,
当x=2时,函数f(x)在[0,3]上取得最小值- 4/3.
例1:求
在[0,3]的最大值与最小值;
又因为f(0)=4,f(3)=1
单调递增
求f(x)在[a,b]上的最大值与最小值的步骤如下:
(1)f(x)在(a,b)内导函数为零的点,并计算出其函数值;
(2)将f(x)的各导数值为零的点的函数值与f(a)、f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
解:(1)因为
x
y′
y
令 解得x= .
单调递减
+
-
0
所以,当x=2时,函数f(x)在[0,3]上取得最大值20,
当x= 时,函数f(x)在[0,3]上取得最小值 .
练习1:求下列函数在给定区间上的最大值与最小值;
又因为f(0)=-2,f(2)=20
单调递增
解:(2)因为
x
y′
y
令 解得 .
单调递减
+
-
0
所以,当x=2时,函数f(x)在 上取得最大值22,
当x= 时,函数f(x)在 上取得最小值 .
练习1:求下列函数在给定区间上的最大值与最小值;
又因为
单调递增
课堂小结
1.最大(小)值的概念
一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:
(1)对于任意的x∈I,都有f(x)≤M; (2)存在x0∈I,使得f(x0) = M
那么,称M是函数y=f(x)的最大值;
设函数y=f(x)的定义域为I,如果存在实数M满足:
(2)对于任意的x∈I,都有f(x)≥M; (2)存在x0∈I,使得f(x0) = M
那么,称M是函数y=f(x)的最小值 。
2.最大(小)值与函数极值的区别与联系
只要把函数y=f(x)的所有极值连同端点的函数值进行比较,就可以求出函数的最大值和最小值。
课堂小结
3.求f(x)在[a,b]上的最大值与最小值的步骤如下:
(1)f(x)在(a,b)内导函数为零的点,并计算出其函数值;
(2)将f(x)的各导数值为零的点的函数值与f(a)、f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
