2020-2021学年高二数学人教A版选修1-2第一章1.2独立性检验的基本思想及其初步应用Word版
文档属性
| 名称 | 2020-2021学年高二数学人教A版选修1-2第一章1.2独立性检验的基本思想及其初步应用Word版 |

|
|
| 格式 | doc | ||
| 文件大小 | 236.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 21:41:15 | ||
图片预览

文档简介
1.2独立性检验的基本思想及其初步应用 (2课时)
【授课时间】 年 月 日 班级:
【教学目标】 1.知识与技能
了解独立性检验的基本思想,会对两个分类变量进行独立性检验,明确独立性检验的基本步骤,并能利用独立性检验的基本思想来解决实际问题。
2.过程与方法
通过设置问题,引导学生自主学习、合作探究、归纳展示,培养学生分析问题、解决问题、团结协作的能力。
3.情感态度与价值观
通过本节课的学习,加强数学与现实生活的联系。以科学的态度评价两个分类变量有关系的可能性,让学生对统计方法有更深刻的认识,体会统计方法应用的广泛性。
【教学重点】理解独立性检验的基本思想及实施步骤
【教学难点】 (1)了解独立性检验的基本思想;
(2)了解随机变量K2的含义,K2的观测值很大,就认为两个分类变量是有关系的。
【课 型】新课
【教学用具】 PPT课件,课本
【教学方法】探究法,提问法,讨论法
【教学过程】
初次备课 二次备课
一、新课引入: (1)你认为吸烟与患肺癌有关系吗?
(2)你会如何使用以下数据反映吸烟与患肺癌的关系?
不患肺癌
患肺癌
总计
不吸烟
7 775
42
7 817
吸烟
2 099
49
2 148
总计
9 874
91
9 965
由以上列联表,我们估计吸烟是否对患肺癌有影响?①在不吸烟者中患肺癌的比例为0.54%;②在吸烟者中患肺癌的比例为2.28%.
二、新课讲授:
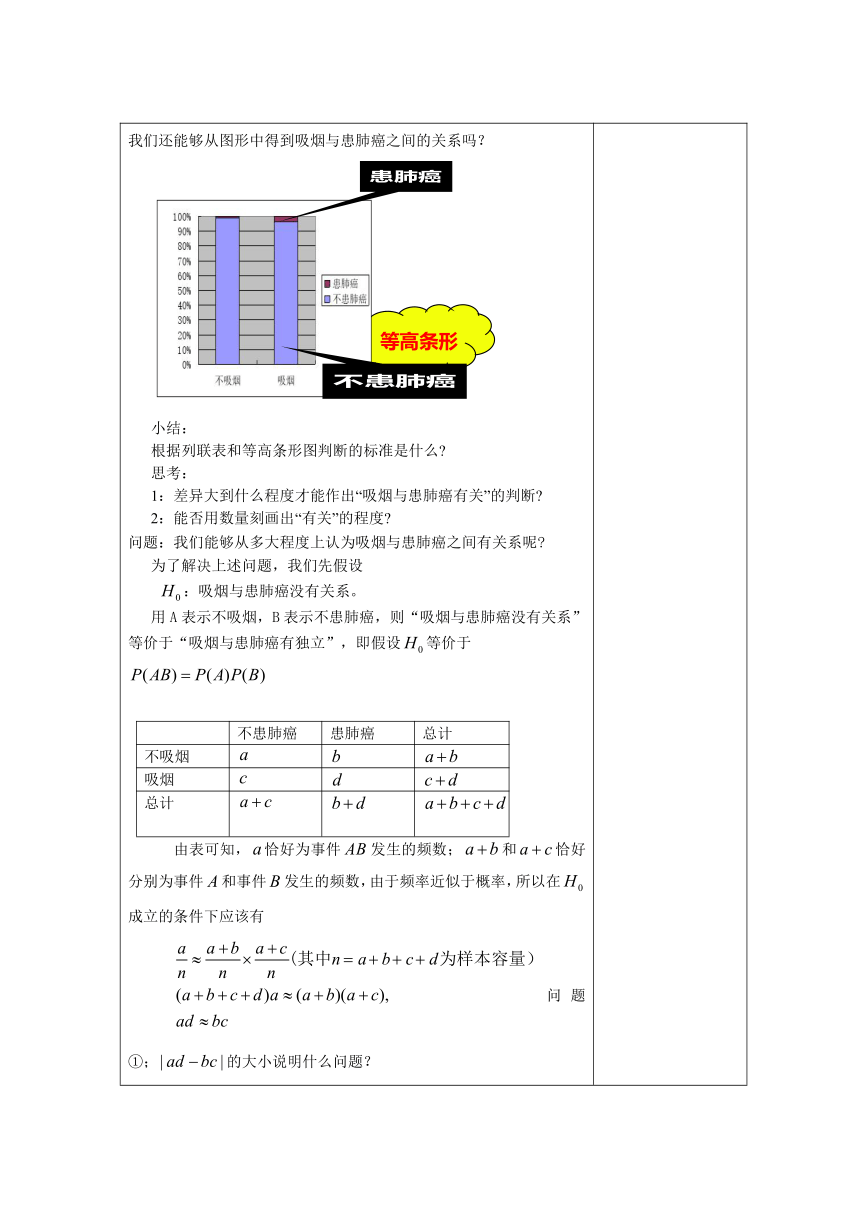
我们还能够从图形中得到吸烟与患肺癌之间的关系吗?
小结:
根据列联表和等高条形图判断的标准是什么?
思考:
1:差异大到什么程度才能作出“吸烟与患肺癌有关”的判断?
2:能否用数量刻画出“有关”的程度?
问题:我们能够从多大程度上认为吸烟与患肺癌之间有关系呢?
为了解决上述问题,我们先假设
:吸烟与患肺癌没有关系。
用A表示不吸烟,B表示不患肺癌,则“吸烟与患肺癌没有关系”等价于“吸烟与患肺癌有独立”,即假设等价于
不患肺癌
患肺癌
总计
不吸烟
吸烟
总计
由表可知,恰好为事件发生的频数;和恰好分别为事件和事件发生的频数,由于频率近似于概率,所以在成立的条件下应该有
问题①;的大小说明什么问题?
因此越小,说明吸烟与患肺癌之间关系越弱;越大,说明吸烟与患肺癌之间关系越强。
为了使不同样本容量的数据有统一的评判标准,基于上述分析,我们构造一个随机变量
其中为样本容量。
问题②:若:吸烟与患肺癌没有关系成立,则应该很小。由公式计算得到的观测值为
这个值到底能告诉我们什么呢?
解读临界值表
p(k≥k0)
0.50
0.40
0.25
0.15
0.10
k0
0.455
0.708
1.323
2.072
2.706
p(k≥k0)
0.05
0.025
0.010
0.005
0.001
k0
3.841
5.024
6.636
7.879
10.828
统计学家经过研究发现,在成立的情况下,
即在成立的情况下,的观测值大于6.635的概率非常小,近似于0.010,是一个小概率事件,假设下小概率事件不该发生。若发生了,就有理由判断不成立。
实际上借助于随机变量的观测值,建立了一个判断是否成立的 规则:
如果,就判断不成立,即吸烟与患肺癌有关系;否则就判断成立,即吸烟与患肺癌没有关系.在该规则下,把结论“成立”错判成“不成立”的概率不会超过,即有的把握认为不成立.
独立性检验定义:这种利用随机变量来判断“两个分类变量有关系”的方法,称为两个分类变量的独立性检验.
三、巩固练习:
在某医院,因为患心脏病而住院的665名男性病人中,有214人秃顶,而另外772名不是因为患心脏病而住院的男性病人中,有175人秃顶.利用图形判断秃顶与患心脏病是否有关系.能否在犯错误的概率不超过0.010的前提下认为秃顶与患心脏病有关系?
答案
解:根据题中的数据得到如下列联表:
相应的等高条形图如图所示:
比较来说,秃顶的病人中患心脏病的比例大一些,可以在某种程度上认为“秃顶与患心脏病有关”.
根据表中数据,得到:
所以在犯错误的概率不超过0.010的前提下认为秃顶与患心脏病有关系.
【板书设计】 “独立性检验”的具体做法步骤:
第一步:根据实际问题需要的可信程度确定临界值;
第二步:利用公式计算随机变量K2的观测值k;
第三步:查对临界值表得出结论.
课堂 小结 反证法
独立检验
要证明结论A
备择假设H
在A不成立的前提下进行推理
在H不成立的条件下,即H成立的条件下进行推理
推出矛盾,意味
着结论A成立
[推出有利于H成立的小概率事件(概率不超过的事件)发生,意味着H成立的可能性(可能性为(1-))很大]
没有找到矛盾,不能对A下任何结论,即反证法不成功
(推出有利于H成立的小概率事件不发生,接受原假设)
【布置作业】 课后习题P15 练习题
备课组长:
教学反思
亮点:
不足及改进措施:
教务处(教学部):
【授课时间】 年 月 日 班级:
【教学目标】 1.知识与技能
了解独立性检验的基本思想,会对两个分类变量进行独立性检验,明确独立性检验的基本步骤,并能利用独立性检验的基本思想来解决实际问题。
2.过程与方法
通过设置问题,引导学生自主学习、合作探究、归纳展示,培养学生分析问题、解决问题、团结协作的能力。
3.情感态度与价值观
通过本节课的学习,加强数学与现实生活的联系。以科学的态度评价两个分类变量有关系的可能性,让学生对统计方法有更深刻的认识,体会统计方法应用的广泛性。
【教学重点】理解独立性检验的基本思想及实施步骤
【教学难点】 (1)了解独立性检验的基本思想;
(2)了解随机变量K2的含义,K2的观测值很大,就认为两个分类变量是有关系的。
【课 型】新课
【教学用具】 PPT课件,课本
【教学方法】探究法,提问法,讨论法
【教学过程】
初次备课 二次备课
一、新课引入: (1)你认为吸烟与患肺癌有关系吗?
(2)你会如何使用以下数据反映吸烟与患肺癌的关系?
不患肺癌
患肺癌
总计
不吸烟
7 775
42
7 817
吸烟
2 099
49
2 148
总计
9 874
91
9 965
由以上列联表,我们估计吸烟是否对患肺癌有影响?①在不吸烟者中患肺癌的比例为0.54%;②在吸烟者中患肺癌的比例为2.28%.
二、新课讲授:
我们还能够从图形中得到吸烟与患肺癌之间的关系吗?
小结:
根据列联表和等高条形图判断的标准是什么?
思考:
1:差异大到什么程度才能作出“吸烟与患肺癌有关”的判断?
2:能否用数量刻画出“有关”的程度?
问题:我们能够从多大程度上认为吸烟与患肺癌之间有关系呢?
为了解决上述问题,我们先假设
:吸烟与患肺癌没有关系。
用A表示不吸烟,B表示不患肺癌,则“吸烟与患肺癌没有关系”等价于“吸烟与患肺癌有独立”,即假设等价于
不患肺癌
患肺癌
总计
不吸烟
吸烟
总计
由表可知,恰好为事件发生的频数;和恰好分别为事件和事件发生的频数,由于频率近似于概率,所以在成立的条件下应该有
问题①;的大小说明什么问题?
因此越小,说明吸烟与患肺癌之间关系越弱;越大,说明吸烟与患肺癌之间关系越强。
为了使不同样本容量的数据有统一的评判标准,基于上述分析,我们构造一个随机变量
其中为样本容量。
问题②:若:吸烟与患肺癌没有关系成立,则应该很小。由公式计算得到的观测值为
这个值到底能告诉我们什么呢?
解读临界值表
p(k≥k0)
0.50
0.40
0.25
0.15
0.10
k0
0.455
0.708
1.323
2.072
2.706
p(k≥k0)
0.05
0.025
0.010
0.005
0.001
k0
3.841
5.024
6.636
7.879
10.828
统计学家经过研究发现,在成立的情况下,
即在成立的情况下,的观测值大于6.635的概率非常小,近似于0.010,是一个小概率事件,假设下小概率事件不该发生。若发生了,就有理由判断不成立。
实际上借助于随机变量的观测值,建立了一个判断是否成立的 规则:
如果,就判断不成立,即吸烟与患肺癌有关系;否则就判断成立,即吸烟与患肺癌没有关系.在该规则下,把结论“成立”错判成“不成立”的概率不会超过,即有的把握认为不成立.
独立性检验定义:这种利用随机变量来判断“两个分类变量有关系”的方法,称为两个分类变量的独立性检验.
三、巩固练习:
在某医院,因为患心脏病而住院的665名男性病人中,有214人秃顶,而另外772名不是因为患心脏病而住院的男性病人中,有175人秃顶.利用图形判断秃顶与患心脏病是否有关系.能否在犯错误的概率不超过0.010的前提下认为秃顶与患心脏病有关系?
答案
解:根据题中的数据得到如下列联表:
相应的等高条形图如图所示:
比较来说,秃顶的病人中患心脏病的比例大一些,可以在某种程度上认为“秃顶与患心脏病有关”.
根据表中数据,得到:
所以在犯错误的概率不超过0.010的前提下认为秃顶与患心脏病有关系.
【板书设计】 “独立性检验”的具体做法步骤:
第一步:根据实际问题需要的可信程度确定临界值;
第二步:利用公式计算随机变量K2的观测值k;
第三步:查对临界值表得出结论.
课堂 小结 反证法
独立检验
要证明结论A
备择假设H
在A不成立的前提下进行推理
在H不成立的条件下,即H成立的条件下进行推理
推出矛盾,意味
着结论A成立
[推出有利于H成立的小概率事件(概率不超过的事件)发生,意味着H成立的可能性(可能性为(1-))很大]
没有找到矛盾,不能对A下任何结论,即反证法不成功
(推出有利于H成立的小概率事件不发生,接受原假设)
【布置作业】 课后习题P15 练习题
备课组长:
教学反思
亮点:
不足及改进措施:
教务处(教学部):
