2020-2021学年高二数学人教A版选修2-2 第二章2.2.2反证法Word版教案
文档属性
| 名称 | 2020-2021学年高二数学人教A版选修2-2 第二章2.2.2反证法Word版教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 48.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 21:51:42 | ||
图片预览

文档简介
【课 题】2.2.2反证法
【授课时间】 年 月 日 班级:
【教学目标】
1.知识与技能
(1) 了解反证法的基本原理; (2) 掌握运用反证法的一般步骤;
(3) 学会用反证法证明一些典型问题.
2.过程与方法
通过学生的参与,激发学生学习数学的兴趣。
3.情感态度与价值观
通过学生的参与,激发学生学习数学的兴趣。
【教学重点】用反证法证明一些典型问题.
【教学难点】用反证法证明一些典型问题.
【课 型】新课
【教学用具】 PPT课件,课本
【教学方法】探究法,提问法,讨论法
【教学过程】
初次备课
二次备课
预习检测:
桌面上有3枚正面朝上的硬币,每次用双手翻转2枚硬币,那么,无论怎样翻转,都不能使硬币全部反面朝上。你能解释这种现象吗?
新课引入:
利用反证法证明不等式的第三步所称的矛盾结果,通常是指所推出的结果与已知公理、定义、定理或已知条件、已证不等式,以及与临时假定矛盾等各种情况。
新课讲授:
3771900453390
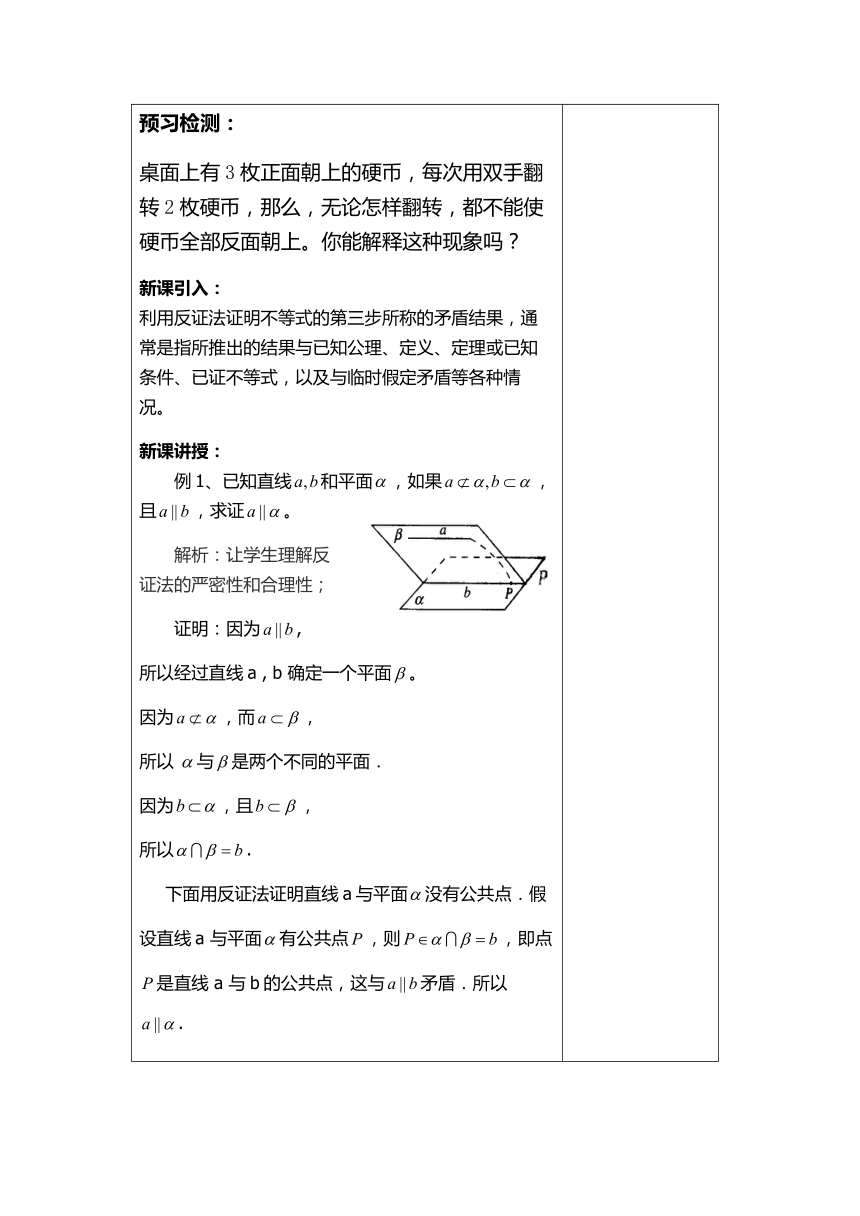
例1、已知直线和平面,如果,且,求证。
解析:让学生理解反证法的严密性和合理性;
证明:因为,
所以经过直线a , b 确定一个平面。
因为,而,
所以 与是两个不同的平面.
因为,且,
所以.
下面用反证法证明直线a与平面没有公共点.假设直线a 与平面有公共点,则,即点是直线 a 与b的公共点,这与矛盾.所以 .
点评:用反证法的基本步骤:
第一步 分清欲证不等式所涉及到的条件和结论;
第二步 作出与所证不等式相反的假定;
第三步 从条件和假定出发,应用证确的推理方法,推出矛盾结果;
第四步 断定产生矛盾结果的原因,在于开始所作的假定不正确,于是原证不等利
例2、求证:不是有理数
解析:直接证明一个数是无理数比较困难,我们采用反证法.假设不是无理数,那么它就是有理数.我们知道,任一有理数都可以写成形如(互质, ”的形式.下面我们看看能否由此推出矛盾.
证明:假设不是无理数,那么它就是有理数.于是,存在互质的正整数,使得,从而有,
因此,,
所以 m 为偶数.于是可设 ( k 是正整数),从而有
,即
所以n也为偶数.这与 m , n 互质矛盾!
由上述矛盾可知假设错误,从而是无理数.
点评:反证法是一种间接证法,它是先提出一个与命题的结论相反的假设,然后,从这个假设出发,经过正确的推理,导致矛盾,从而否定相反的假设,达到肯定原命题正确的一种方法。
例3、设二次函数, 求证:中至少有一个不小于.
解析:直接证明中至少有一个不小于.比较困难,我们应采用反证法
证明:假设都小于,则
(1)
另一方面,由绝对值不等式的性质,有
(2)
(1)、(2)两式的结果矛盾,所以假设不成立,原来的结论正确。
结论为“至少”、“至多”等时,我们应考虑用反证法解决。
巩固练习:
1. 证明不可能成等差数列.
2.设,求证
【板书设计】
2.2.2反证法
新课引入 例题1、
例题2、 例题3
巩固练习
课堂
小结
反证法是一种间接证法,它是先提出一个与命题的结论相反的假设,然后,从这个假设出发,经过正确的推理,导致矛盾,从而否定相反的假设,达到肯定原命题正确的一种方法。反证法可以分为归谬反证法(结论的反面只有一种)与穷举反证法(结论的反面不只一种)。用反证法证明一个命题的步骤,大体上分为:(1)反设;(2)归谬;(3)结论。
【布置作业】 课后练习题1、2
备课组长:
教学反思
亮点:
不足及改进措施:
教务处(教学部):
【授课时间】 年 月 日 班级:
【教学目标】
1.知识与技能
(1) 了解反证法的基本原理; (2) 掌握运用反证法的一般步骤;
(3) 学会用反证法证明一些典型问题.
2.过程与方法
通过学生的参与,激发学生学习数学的兴趣。
3.情感态度与价值观
通过学生的参与,激发学生学习数学的兴趣。
【教学重点】用反证法证明一些典型问题.
【教学难点】用反证法证明一些典型问题.
【课 型】新课
【教学用具】 PPT课件,课本
【教学方法】探究法,提问法,讨论法
【教学过程】
初次备课
二次备课
预习检测:
桌面上有3枚正面朝上的硬币,每次用双手翻转2枚硬币,那么,无论怎样翻转,都不能使硬币全部反面朝上。你能解释这种现象吗?
新课引入:
利用反证法证明不等式的第三步所称的矛盾结果,通常是指所推出的结果与已知公理、定义、定理或已知条件、已证不等式,以及与临时假定矛盾等各种情况。
新课讲授:
3771900453390
例1、已知直线和平面,如果,且,求证。
解析:让学生理解反证法的严密性和合理性;
证明:因为,
所以经过直线a , b 确定一个平面。
因为,而,
所以 与是两个不同的平面.
因为,且,
所以.
下面用反证法证明直线a与平面没有公共点.假设直线a 与平面有公共点,则,即点是直线 a 与b的公共点,这与矛盾.所以 .
点评:用反证法的基本步骤:
第一步 分清欲证不等式所涉及到的条件和结论;
第二步 作出与所证不等式相反的假定;
第三步 从条件和假定出发,应用证确的推理方法,推出矛盾结果;
第四步 断定产生矛盾结果的原因,在于开始所作的假定不正确,于是原证不等利
例2、求证:不是有理数
解析:直接证明一个数是无理数比较困难,我们采用反证法.假设不是无理数,那么它就是有理数.我们知道,任一有理数都可以写成形如(互质, ”的形式.下面我们看看能否由此推出矛盾.
证明:假设不是无理数,那么它就是有理数.于是,存在互质的正整数,使得,从而有,
因此,,
所以 m 为偶数.于是可设 ( k 是正整数),从而有
,即
所以n也为偶数.这与 m , n 互质矛盾!
由上述矛盾可知假设错误,从而是无理数.
点评:反证法是一种间接证法,它是先提出一个与命题的结论相反的假设,然后,从这个假设出发,经过正确的推理,导致矛盾,从而否定相反的假设,达到肯定原命题正确的一种方法。
例3、设二次函数, 求证:中至少有一个不小于.
解析:直接证明中至少有一个不小于.比较困难,我们应采用反证法
证明:假设都小于,则
(1)
另一方面,由绝对值不等式的性质,有
(2)
(1)、(2)两式的结果矛盾,所以假设不成立,原来的结论正确。
结论为“至少”、“至多”等时,我们应考虑用反证法解决。
巩固练习:
1. 证明不可能成等差数列.
2.设,求证
【板书设计】
2.2.2反证法
新课引入 例题1、
例题2、 例题3
巩固练习
课堂
小结
反证法是一种间接证法,它是先提出一个与命题的结论相反的假设,然后,从这个假设出发,经过正确的推理,导致矛盾,从而否定相反的假设,达到肯定原命题正确的一种方法。反证法可以分为归谬反证法(结论的反面只有一种)与穷举反证法(结论的反面不只一种)。用反证法证明一个命题的步骤,大体上分为:(1)反设;(2)归谬;(3)结论。
【布置作业】 课后练习题1、2
备课组长:
教学反思
亮点:
不足及改进措施:
教务处(教学部):
