2020-2021学年高一数学人教A版必修二4.2.1 直线与圆的位置关系课件(共21张PPT)
文档属性
| 名称 | 2020-2021学年高一数学人教A版必修二4.2.1 直线与圆的位置关系课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 969.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 00:00:00 | ||
图片预览





文档简介
4.2.1 直线与圆的位置关系
情境引入
情境引入
情境:“海上生明月,天涯共此时。”一年一度的中秋节即将到来,上图为一幅海边赏月图,若把海平面看作一条直线,把月亮看成一个圆,则在月亮升起的过程中,反映了直线与圆的哪些位置关系呢?
情境引入
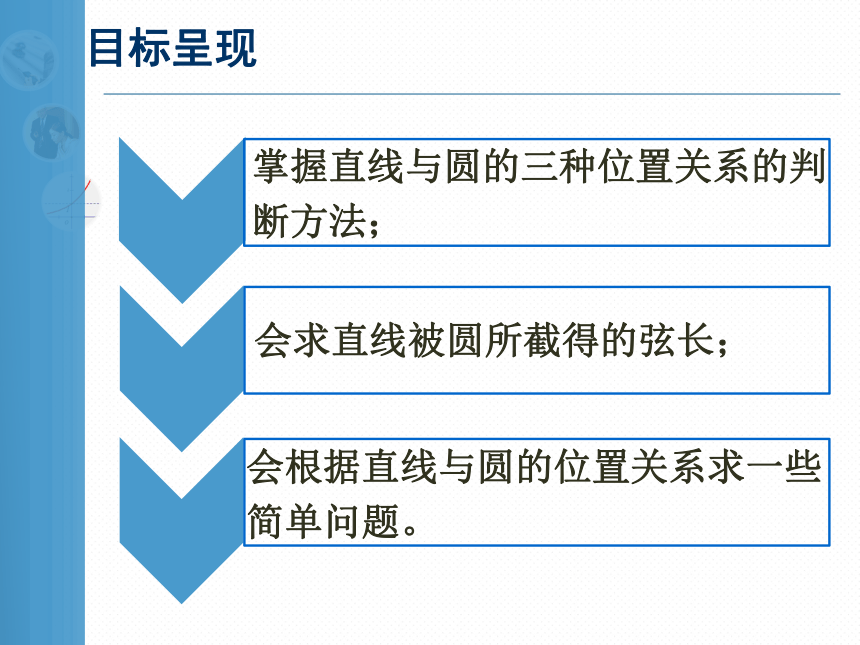
目标呈现
掌握直线与圆的三种位置关系的判断方法;
会求直线被圆所截得的弦长;
会根据直线与圆的位置关系求一些简单问题。
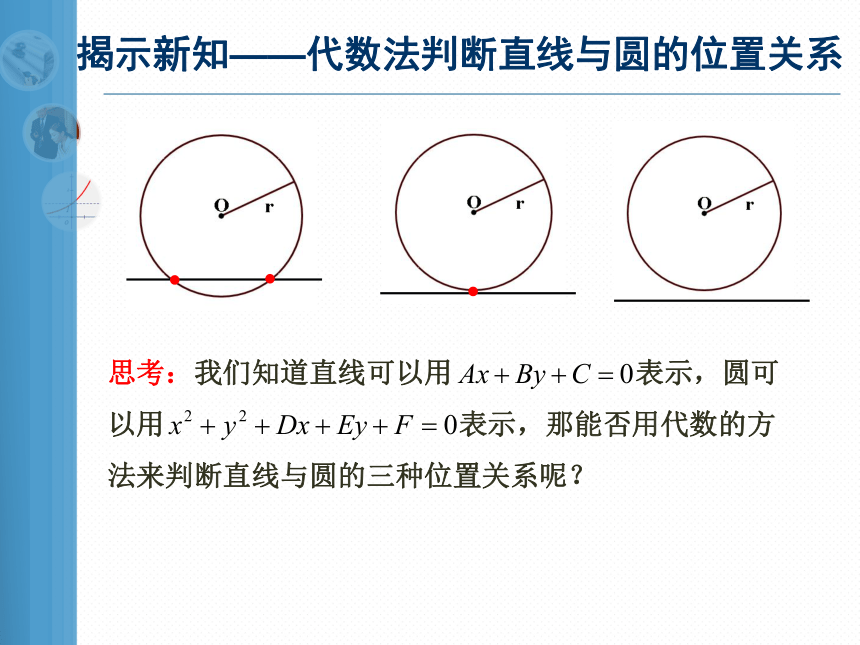
揭示新知——代数法判断直线与圆的位置关系
思考:我们知道直线可以用 表示,圆可以用 表示,那能否用代数的方法来判断直线与圆的三种位置关系呢?
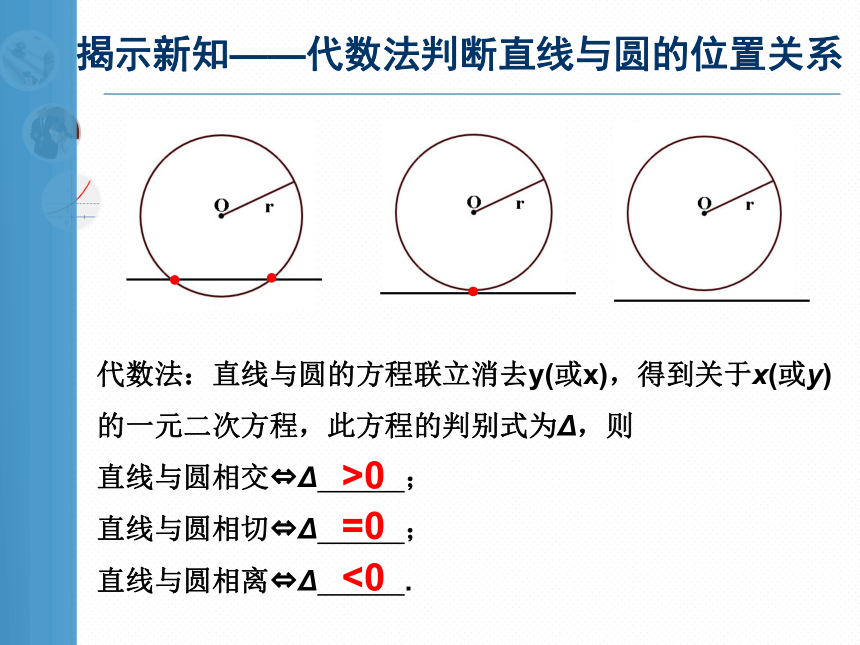
揭示新知——代数法判断直线与圆的位置关系
代数法:直线与圆的方程联立消去y(或x),得到关于x(或y)的一元二次方程,此方程的判别式为Δ,则
直线与圆相交?Δ ;
直线与圆相切?Δ ;
直线与圆相离?Δ .
=0
<0
>0
牛刀小试
1.判断下列命题是否正确.
(1)如果直线与圆组成的方程组有解,则直线与圆相交或相切. ( )
(2)直线x+2y-1=0与圆x2+y2-2x-y+1=0
的位置关系是相交.( )
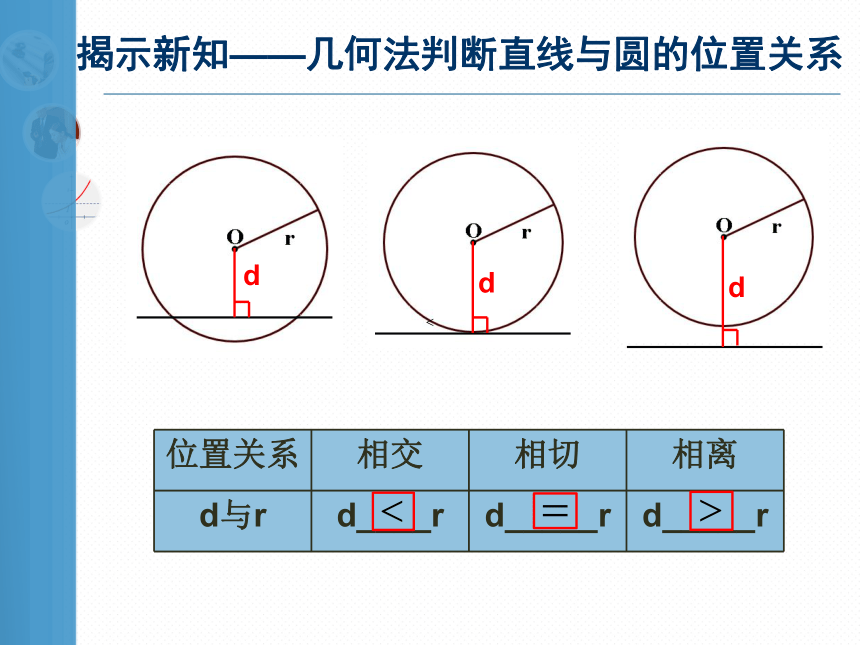
揭示新知——几何法判断直线与圆的位置关系
位置关系
相交
相切
相离
d与r
d____r
d_____r
d_____r
d
d
d
回顾旧知
1.圆的标准方程_________________________,圆心_______,半径______.
2.圆心 到直线 的距离
公式为___________________________.
范例讲解
例1.已知直线 :3x+y-6=0和圆心为C的圆
x2+y2-2y-4=0,
(1)判断直线 与圆C的位置关系;
(2)如果相交,求它们的交点的坐标.
解:(1)法一:圆x2+y2-2y-4=0可化为 ,
圆心C(0,1),半径r= ,圆心C到直线 的距离
∴直线 与圆相交,有两个交点
范例讲解
例1.已知直线 :3x+y-6=0和圆心为C的圆
x2+y2-2y-4=0,
(1)判断直线 与圆C的位置关系;
(2)如果相交,求它们的交点的坐标.
解:(1)法二:由直线 与圆的方程,得
消y,得
∵ ,∴直线 与圆相交,有两交点
范例讲解
例1.已知直线 :3x+y-6=0和圆心为C的圆
x2+y2-2y-4=0,
(1)判断直线 与圆C的位置关系;
(2)如果相交,求它们的交点的坐标.
解:(2)由 ,解得
把 代入,得
把 代入,得
∴两个交点坐标分别为
同学们能说说几何法和代数法判断直线与圆位置关系的具体步骤吗?
方法小结
直线与圆的位置关系
法一:几何法
求圆心,半径r;
求圆心到直线的距离d;
比较d与r
法二:代数法(可求交点坐标)
联立方程组,消y(或x);
得到x(或y)的一元二次方程,求根的判别式△
变式训练
例1.已知直线 :3x+y-6=0和圆心为C的圆
x2+y2-2y-4=0,
(1)判断直线 与圆C的位置关系;
(2)如果相交,求它们的交点的坐标;
(3)如果相交,求出直线被圆所截得的弦长|AB|.
解:(3)由(2)知,两个交点坐标分别为
∴
思考:直线与圆相交,还有其他方法求弦长吗?
弦长问题
d
A
B
r
思考:直线与圆相交,还有其他方法求弦长吗?
牛刀小试
1.直线 被圆
所截得的弦长是 ( )
A.1 B.2 C.3 D.4
B
2.判断直线 和圆 的位置
关系,若相交,求出直线被圆所截得的弦长.
变式1.若直线 和圆 有如下关系:(1)相交;(2)相切;(3)相离,试分别求满足条件的 的范围
课堂小结
1.本节课我们学习了哪些知识呢?
能力提升
例2.已知过点 的直线 被圆
所截得的弦长为 ,求直线 的方程.
能力提升
解:将圆的方程写成标准形式,得 ,
圆心(0,-2),r=5
设直线 的方程为 ,即
两边平方并整理得 ,解得
∴所求方程为
∵直线 被圆所截得的弦长为 ,
∴圆心到直线 的距离为
高考链接
1.(2019.重庆一中模拟)在平面直角坐标系xoy中,点
,直线 与直线 的交点坐标为圆C的圆心,设圆C的半径为1,过点A作斜率为 的直线n交圆C于A、B两点,求弦AB的长.
2.(2019.吉林省实验中学模拟)已知圆M过
两点,且圆心M在直线 上,求圆M的方程 .
情境引入
情境引入
情境:“海上生明月,天涯共此时。”一年一度的中秋节即将到来,上图为一幅海边赏月图,若把海平面看作一条直线,把月亮看成一个圆,则在月亮升起的过程中,反映了直线与圆的哪些位置关系呢?
情境引入
目标呈现
掌握直线与圆的三种位置关系的判断方法;
会求直线被圆所截得的弦长;
会根据直线与圆的位置关系求一些简单问题。
揭示新知——代数法判断直线与圆的位置关系
思考:我们知道直线可以用 表示,圆可以用 表示,那能否用代数的方法来判断直线与圆的三种位置关系呢?
揭示新知——代数法判断直线与圆的位置关系
代数法:直线与圆的方程联立消去y(或x),得到关于x(或y)的一元二次方程,此方程的判别式为Δ,则
直线与圆相交?Δ ;
直线与圆相切?Δ ;
直线与圆相离?Δ .
=0
<0
>0
牛刀小试
1.判断下列命题是否正确.
(1)如果直线与圆组成的方程组有解,则直线与圆相交或相切. ( )
(2)直线x+2y-1=0与圆x2+y2-2x-y+1=0
的位置关系是相交.( )
揭示新知——几何法判断直线与圆的位置关系
位置关系
相交
相切
相离
d与r
d____r
d_____r
d_____r
d
d
d
回顾旧知
1.圆的标准方程_________________________,圆心_______,半径______.
2.圆心 到直线 的距离
公式为___________________________.
范例讲解
例1.已知直线 :3x+y-6=0和圆心为C的圆
x2+y2-2y-4=0,
(1)判断直线 与圆C的位置关系;
(2)如果相交,求它们的交点的坐标.
解:(1)法一:圆x2+y2-2y-4=0可化为 ,
圆心C(0,1),半径r= ,圆心C到直线 的距离
∴直线 与圆相交,有两个交点
范例讲解
例1.已知直线 :3x+y-6=0和圆心为C的圆
x2+y2-2y-4=0,
(1)判断直线 与圆C的位置关系;
(2)如果相交,求它们的交点的坐标.
解:(1)法二:由直线 与圆的方程,得
消y,得
∵ ,∴直线 与圆相交,有两交点
范例讲解
例1.已知直线 :3x+y-6=0和圆心为C的圆
x2+y2-2y-4=0,
(1)判断直线 与圆C的位置关系;
(2)如果相交,求它们的交点的坐标.
解:(2)由 ,解得
把 代入,得
把 代入,得
∴两个交点坐标分别为
同学们能说说几何法和代数法判断直线与圆位置关系的具体步骤吗?
方法小结
直线与圆的位置关系
法一:几何法
求圆心,半径r;
求圆心到直线的距离d;
比较d与r
法二:代数法(可求交点坐标)
联立方程组,消y(或x);
得到x(或y)的一元二次方程,求根的判别式△
变式训练
例1.已知直线 :3x+y-6=0和圆心为C的圆
x2+y2-2y-4=0,
(1)判断直线 与圆C的位置关系;
(2)如果相交,求它们的交点的坐标;
(3)如果相交,求出直线被圆所截得的弦长|AB|.
解:(3)由(2)知,两个交点坐标分别为
∴
思考:直线与圆相交,还有其他方法求弦长吗?
弦长问题
d
A
B
r
思考:直线与圆相交,还有其他方法求弦长吗?
牛刀小试
1.直线 被圆
所截得的弦长是 ( )
A.1 B.2 C.3 D.4
B
2.判断直线 和圆 的位置
关系,若相交,求出直线被圆所截得的弦长.
变式1.若直线 和圆 有如下关系:(1)相交;(2)相切;(3)相离,试分别求满足条件的 的范围
课堂小结
1.本节课我们学习了哪些知识呢?
能力提升
例2.已知过点 的直线 被圆
所截得的弦长为 ,求直线 的方程.
能力提升
解:将圆的方程写成标准形式,得 ,
圆心(0,-2),r=5
设直线 的方程为 ,即
两边平方并整理得 ,解得
∴所求方程为
∵直线 被圆所截得的弦长为 ,
∴圆心到直线 的距离为
高考链接
1.(2019.重庆一中模拟)在平面直角坐标系xoy中,点
,直线 与直线 的交点坐标为圆C的圆心,设圆C的半径为1,过点A作斜率为 的直线n交圆C于A、B两点,求弦AB的长.
2.(2019.吉林省实验中学模拟)已知圆M过
两点,且圆心M在直线 上,求圆M的方程 .
