2020--2021学年九年级数学人教版下册 第二十七章 《相似》 常考题强化练习(Word版 含答案)
文档属性
| 名称 | 2020--2021学年九年级数学人教版下册 第二十七章 《相似》 常考题强化练习(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 188.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-22 17:04:06 | ||
图片预览



文档简介
2020--2021学年九年级下册数学第二十七章 《相似》
常考题强化练习(一)
1.阅读与计算,请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理,如图1,在△ABC中,AD平分∠BAC,则=.下面是这个定理的部分证明过程.
证明:如图2,过C作CE∥DA.交BA的延长线于E.…
任务:
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)填空:如图3,已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,则△ABD的周长是 .
2.已知:如图,△ABC是等边三角形,点D、E分别在边BC、AC上,∠ADE=60°.
(1)求证:△ABD∽△DCE;
(2)如果AB=3,EC=,求DC的长.
3.如图,在矩形ABCD中,AB=4,AD=10.一把三角尺的直角顶点P在AD上滑动时(点P与A、D不重合),一直角边始终经过点C,另一直角边与AB交于点E.
(1)证明△DPC∽△AEP;
(2)当∠CPD=30°时,求AE的长;
(3)是否存在这样的点P,使△DPC的周长等于△AEP周长的2倍?若存在,求出DP的长;若不存在,请说明理由.
4.如图,建筑物BC上有一个旗杆AB,小明和数学兴趣小组的同学计划用学过的知识测量该建筑物的高度,他们制订了测量方案,并利用课余时间完成了实地测量,测量方法如下:在该建筑物底部所在的平地上有一棵小树ED,小明沿CD后退,发现地面上的点F、树顶E、旗杆顶端A恰好在一条直线上,继续后退,发现地面上的点G、树顶E、建筑物顶端B恰好在一条直线上,已知旗杆AB=3米,DE=4米,DF=5米,FG=1.5米,点A、B、C在一条直线上,点C、D、F、G在一条直线上,AC、ED均垂直于CG,根据以上信息,请求出这座建筑物的高BC.
5.如图,在△ABC中,BC=3,D为AC延长线上一点,AC=3CD,∠CBD=∠A,过D作DH∥AB,交BC的延长线于点H.
(1)求证:△HCD∽△HDB.
(2)求DH长度.
6.如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF:DC=1:4,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为10,求BG的长.
7.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6,AF=4,求AE的长.
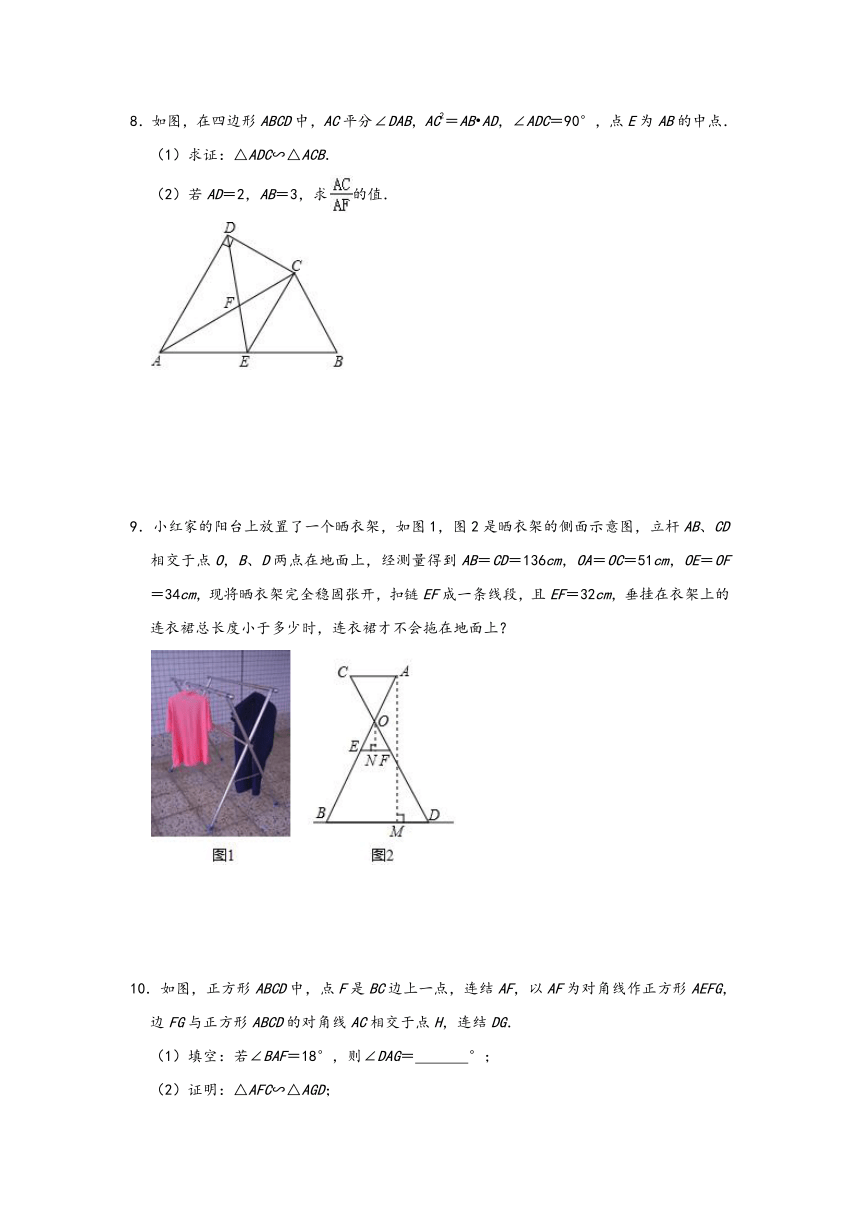
8.如图,在四边形ABCD中,AC平分∠DAB,AC2=AB?AD,∠ADC=90°,点E为AB的中点.
(1)求证:△ADC∽△ACB.
(2)若AD=2,AB=3,求的值.
9.小红家的阳台上放置了一个晒衣架,如图1,图2是晒衣架的侧面示意图,立杆AB、CD相交于点O,B、D两点在地面上,经测量得到AB=CD=136cm,OA=OC=51cm,OE=OF=34cm,现将晒衣架完全稳固张开,扣链EF成一条线段,且EF=32cm,垂挂在衣架上的连衣裙总长度小于多少时,连衣裙才不会拖在地面上?
10.如图,正方形ABCD中,点F是BC边上一点,连结AF,以AF为对角线作正方形AEFG,边FG与正方形ABCD的对角线AC相交于点H,连结DG.
(1)填空:若∠BAF=18°,则∠DAG= °;
(2)证明:△AFC∽△AGD;
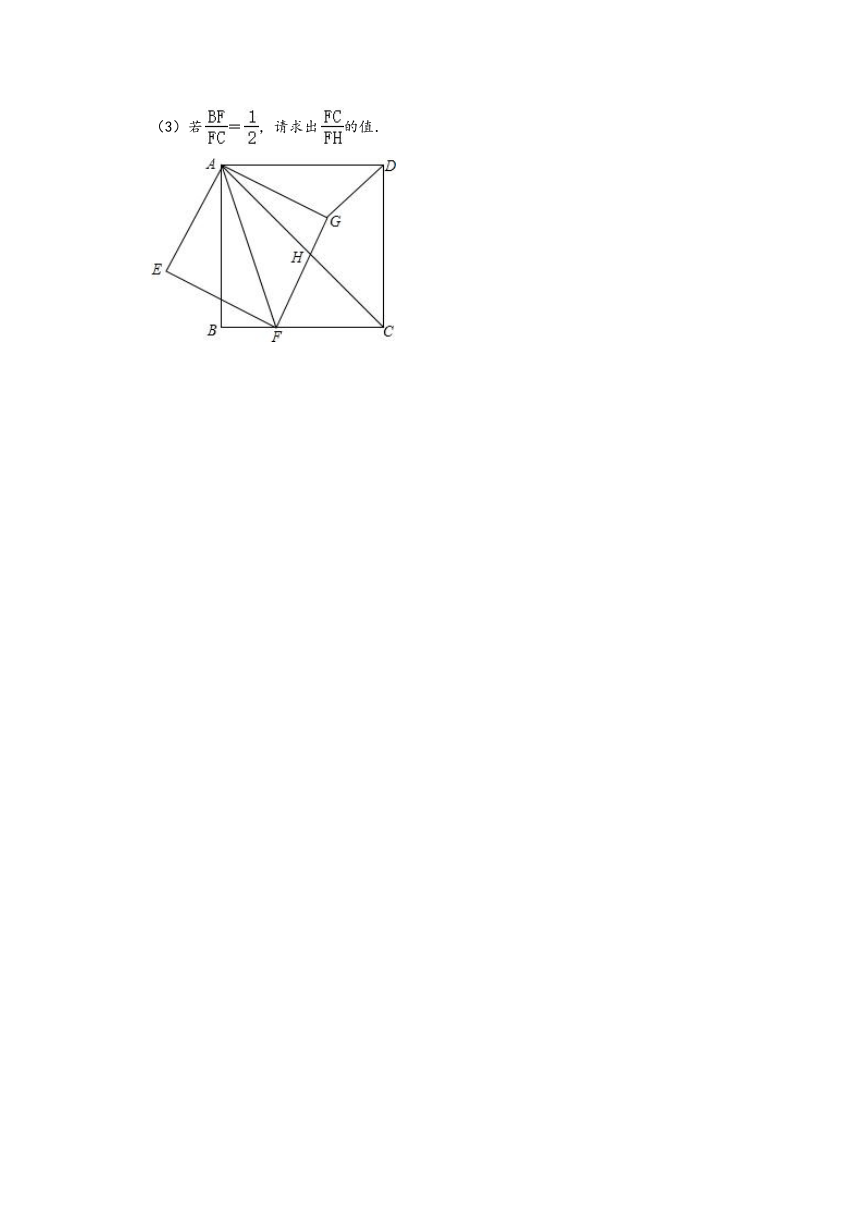
(3)若=,请求出的值.
参考答案
1.(1)证明:如图2,过C作CE∥DA.交BA的延长线于E,
∵CE∥AD,
∴=,∠2=∠ACE,∠1=∠E,
∵∠1=∠2,
∴∠ACE=∠E,
∴AE=AC,
∴=;
(2)解:如图3,∵AB=3,BC=4,∠ABC=90°,
∴AC=5,
∵AD平分∠BAC,
∴=,即=,
∴BD=BC=,
∴AD===,
∴△ABD的周长=+3+=.
故答案为.
2.(1)证明:∵△ABC是等边三角形,
∴∠B=∠C=60°,AB=AC,
∵∠B+∠BAD=∠ADE+∠CDE,∠B=∠ADE=60°,
∴∠BAD=∠CDE
∴△ABD∽△DCE;
(2)解:由(1)证得△ABD∽△DCE,
∴=,
设CD=x,则BD=3﹣x,
∴=,
∴x=1或x=2,
∴DC=1或DC=2.
3.解:(1)证明:在△DPC、△AEP中,∠1与∠2互余,∠2与∠3互余,
∴∠1=∠3,
又∠A=∠D=90°,
∴△DPC∽△AEP.
(2)∵∠2=30°,CD=4,
∴PC=8,PD=,
又∵AD=10,
∴AP=AD﹣PD=10﹣4,
由(1),得=10﹣12;
(3)存在这样的点P,使△DPC的周长等于△AEP周长的2倍,
∵相似三角形周长的比等于相似比,设=2,
解得DP=8.
4.解:由题意可得,∠ACF=∠EDF=90°,∠AFC=∠EFD,
∴△ACF∽△EDF,
∴,即,
∴CD=,
由题意可得,∠BCG=∠EDG=90°,∠BGC=∠EGD,
∴△BCG∽△EDG,
∴,即,
∴6.5BC=4(CD+6.5),
∴6.5BC=4×,
∴BC=14,
∴这座建筑物的高BC为14米.
5.解:(1)证明:∵DH∥AB,
∴∠A=∠HDC,
∵∠CBD=∠A,
∴∠HDC=∠CBD,又∠H=∠H,
∴△HCD∽△HDB;
(2)∵DH∥AB,
∴=,
∵AC=3CD,
∴=,
∴CH=1,
∴BH=BC+CH=3+1=4,
由(1)知△HCD∽△HDB,
∴=,
∴DH2=4×1=4,
∴DH=2(负值舍去).
答:DH的长度为2.
6.证明:∵四边形ABCD是正方形,
∴∠A=∠D=90°,AB=AD=CD,
∵AE=ED,DF:DC=1:4,
∴AE=DE=AD=AB,DF=CD=AD,
∵,=
∴,且∠A=∠D,
∴△ABE∽△DEF
(2)∵CB=AD=CD=10,
∴AE=DE=5,DF=,CF=
∵AD∥BC
∴△DEF∽△CGF
∴,即
∴CG=15
∴BG=BC+CG=10+15=25
7.(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,
∴∠C+∠B=180°,∠ADF=∠DEC.
∵∠AFD+∠AFE=180°,∠AFE=∠B,
∴∠AFD=∠C.
∴△ADF∽△DEC.
(2)解:∵四边形ABCD是平行四边形,∴CD=AB=8.
由(1)知△ADF∽△DEC,
∴=,
∴DE===12.
在Rt△ADE中,由勾股定理得:AE==6.
8.(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵AC2=AB?AD,
∴=,
∴△ADC∽△ACB;
(2)∵△ADC∽△ACB,
∴∠ACB=∠ADC=90°,
∵点E为AB的中点,
∴CE=AE=AB=,
∴∠EAC=∠ECA,
∴∠DAC=∠EAC,
∴∠DAC=∠ECA,
∴CE∥AD;
∴==,
∴=.
9.解:∵AB、CD相交于点O,
∴∠AOC=∠BOD
∵OA=OC,
∴∠OAC=∠OCA=(180°﹣∠BOD),
同理可证:∠OBD=∠ODB=(180°﹣∠BOD),
∴∠OAC=∠OBD,
∴AC∥BD,
在Rt△OEN中,ON==30(cm),
过点A作AM⊥BD于点M,
同理可证:EF∥BD,
∴∠ABM=∠OEN,则Rt△OEN∽Rt△ABM,
∴=,AM==120(cm),
所以垂挂在衣架上的连衣裙总长度小于120cm时,连衣裙才不会拖落到地面上.
10.解:(1)∵四边形ABCD,AEFG是正方形,
∴∠BAC=∠GAF=45°,
∴∠BAF+∠FAC=∠FAC+∠GAC=45°,
∴∠HAG=∠BAF=18°,
∵∠DAG+∠GAH=∠DAC=45°,
∴∠DAG=45°﹣18°=27°,
故答案为:27.
(2)∵四边形ABCD,AEFG是正方形,
∴=,=,
∴=,
∵∠DAG+∠GAC=∠FAC+∠GAC=45°,
∴∠DAG=∠CAF,
∴△AFC∽△AGD;
(3)∵=,
设BF=k,CF=2k,则AB=BC=3k,
∴AF===k,AC=AB=3k,
∵四边形ABCD,AEFG是正方形,
∴∠AFH=∠ACF,∠FAH=∠CAF,
∴△AFH∽△ACF,
∴=,
∴==.
常考题强化练习(一)
1.阅读与计算,请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理,如图1,在△ABC中,AD平分∠BAC,则=.下面是这个定理的部分证明过程.
证明:如图2,过C作CE∥DA.交BA的延长线于E.…
任务:
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)填空:如图3,已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,则△ABD的周长是 .
2.已知:如图,△ABC是等边三角形,点D、E分别在边BC、AC上,∠ADE=60°.
(1)求证:△ABD∽△DCE;
(2)如果AB=3,EC=,求DC的长.
3.如图,在矩形ABCD中,AB=4,AD=10.一把三角尺的直角顶点P在AD上滑动时(点P与A、D不重合),一直角边始终经过点C,另一直角边与AB交于点E.
(1)证明△DPC∽△AEP;
(2)当∠CPD=30°时,求AE的长;
(3)是否存在这样的点P,使△DPC的周长等于△AEP周长的2倍?若存在,求出DP的长;若不存在,请说明理由.
4.如图,建筑物BC上有一个旗杆AB,小明和数学兴趣小组的同学计划用学过的知识测量该建筑物的高度,他们制订了测量方案,并利用课余时间完成了实地测量,测量方法如下:在该建筑物底部所在的平地上有一棵小树ED,小明沿CD后退,发现地面上的点F、树顶E、旗杆顶端A恰好在一条直线上,继续后退,发现地面上的点G、树顶E、建筑物顶端B恰好在一条直线上,已知旗杆AB=3米,DE=4米,DF=5米,FG=1.5米,点A、B、C在一条直线上,点C、D、F、G在一条直线上,AC、ED均垂直于CG,根据以上信息,请求出这座建筑物的高BC.
5.如图,在△ABC中,BC=3,D为AC延长线上一点,AC=3CD,∠CBD=∠A,过D作DH∥AB,交BC的延长线于点H.
(1)求证:△HCD∽△HDB.
(2)求DH长度.
6.如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF:DC=1:4,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为10,求BG的长.
7.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6,AF=4,求AE的长.
8.如图,在四边形ABCD中,AC平分∠DAB,AC2=AB?AD,∠ADC=90°,点E为AB的中点.
(1)求证:△ADC∽△ACB.
(2)若AD=2,AB=3,求的值.
9.小红家的阳台上放置了一个晒衣架,如图1,图2是晒衣架的侧面示意图,立杆AB、CD相交于点O,B、D两点在地面上,经测量得到AB=CD=136cm,OA=OC=51cm,OE=OF=34cm,现将晒衣架完全稳固张开,扣链EF成一条线段,且EF=32cm,垂挂在衣架上的连衣裙总长度小于多少时,连衣裙才不会拖在地面上?
10.如图,正方形ABCD中,点F是BC边上一点,连结AF,以AF为对角线作正方形AEFG,边FG与正方形ABCD的对角线AC相交于点H,连结DG.
(1)填空:若∠BAF=18°,则∠DAG= °;
(2)证明:△AFC∽△AGD;
(3)若=,请求出的值.
参考答案
1.(1)证明:如图2,过C作CE∥DA.交BA的延长线于E,
∵CE∥AD,
∴=,∠2=∠ACE,∠1=∠E,
∵∠1=∠2,
∴∠ACE=∠E,
∴AE=AC,
∴=;
(2)解:如图3,∵AB=3,BC=4,∠ABC=90°,
∴AC=5,
∵AD平分∠BAC,
∴=,即=,
∴BD=BC=,
∴AD===,
∴△ABD的周长=+3+=.
故答案为.
2.(1)证明:∵△ABC是等边三角形,
∴∠B=∠C=60°,AB=AC,
∵∠B+∠BAD=∠ADE+∠CDE,∠B=∠ADE=60°,
∴∠BAD=∠CDE
∴△ABD∽△DCE;
(2)解:由(1)证得△ABD∽△DCE,
∴=,
设CD=x,则BD=3﹣x,
∴=,
∴x=1或x=2,
∴DC=1或DC=2.
3.解:(1)证明:在△DPC、△AEP中,∠1与∠2互余,∠2与∠3互余,
∴∠1=∠3,
又∠A=∠D=90°,
∴△DPC∽△AEP.
(2)∵∠2=30°,CD=4,
∴PC=8,PD=,
又∵AD=10,
∴AP=AD﹣PD=10﹣4,
由(1),得=10﹣12;
(3)存在这样的点P,使△DPC的周长等于△AEP周长的2倍,
∵相似三角形周长的比等于相似比,设=2,
解得DP=8.
4.解:由题意可得,∠ACF=∠EDF=90°,∠AFC=∠EFD,
∴△ACF∽△EDF,
∴,即,
∴CD=,
由题意可得,∠BCG=∠EDG=90°,∠BGC=∠EGD,
∴△BCG∽△EDG,
∴,即,
∴6.5BC=4(CD+6.5),
∴6.5BC=4×,
∴BC=14,
∴这座建筑物的高BC为14米.
5.解:(1)证明:∵DH∥AB,
∴∠A=∠HDC,
∵∠CBD=∠A,
∴∠HDC=∠CBD,又∠H=∠H,
∴△HCD∽△HDB;
(2)∵DH∥AB,
∴=,
∵AC=3CD,
∴=,
∴CH=1,
∴BH=BC+CH=3+1=4,
由(1)知△HCD∽△HDB,
∴=,
∴DH2=4×1=4,
∴DH=2(负值舍去).
答:DH的长度为2.
6.证明:∵四边形ABCD是正方形,
∴∠A=∠D=90°,AB=AD=CD,
∵AE=ED,DF:DC=1:4,
∴AE=DE=AD=AB,DF=CD=AD,
∵,=
∴,且∠A=∠D,
∴△ABE∽△DEF
(2)∵CB=AD=CD=10,
∴AE=DE=5,DF=,CF=
∵AD∥BC
∴△DEF∽△CGF
∴,即
∴CG=15
∴BG=BC+CG=10+15=25
7.(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,
∴∠C+∠B=180°,∠ADF=∠DEC.
∵∠AFD+∠AFE=180°,∠AFE=∠B,
∴∠AFD=∠C.
∴△ADF∽△DEC.
(2)解:∵四边形ABCD是平行四边形,∴CD=AB=8.
由(1)知△ADF∽△DEC,
∴=,
∴DE===12.
在Rt△ADE中,由勾股定理得:AE==6.
8.(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵AC2=AB?AD,
∴=,
∴△ADC∽△ACB;
(2)∵△ADC∽△ACB,
∴∠ACB=∠ADC=90°,
∵点E为AB的中点,
∴CE=AE=AB=,
∴∠EAC=∠ECA,
∴∠DAC=∠EAC,
∴∠DAC=∠ECA,
∴CE∥AD;
∴==,
∴=.
9.解:∵AB、CD相交于点O,
∴∠AOC=∠BOD
∵OA=OC,
∴∠OAC=∠OCA=(180°﹣∠BOD),
同理可证:∠OBD=∠ODB=(180°﹣∠BOD),
∴∠OAC=∠OBD,
∴AC∥BD,
在Rt△OEN中,ON==30(cm),
过点A作AM⊥BD于点M,
同理可证:EF∥BD,
∴∠ABM=∠OEN,则Rt△OEN∽Rt△ABM,
∴=,AM==120(cm),
所以垂挂在衣架上的连衣裙总长度小于120cm时,连衣裙才不会拖落到地面上.
10.解:(1)∵四边形ABCD,AEFG是正方形,
∴∠BAC=∠GAF=45°,
∴∠BAF+∠FAC=∠FAC+∠GAC=45°,
∴∠HAG=∠BAF=18°,
∵∠DAG+∠GAH=∠DAC=45°,
∴∠DAG=45°﹣18°=27°,
故答案为:27.
(2)∵四边形ABCD,AEFG是正方形,
∴=,=,
∴=,
∵∠DAG+∠GAC=∠FAC+∠GAC=45°,
∴∠DAG=∠CAF,
∴△AFC∽△AGD;
(3)∵=,
设BF=k,CF=2k,则AB=BC=3k,
∴AF===k,AC=AB=3k,
∵四边形ABCD,AEFG是正方形,
∴∠AFH=∠ACF,∠FAH=∠CAF,
∴△AFH∽△ACF,
∴=,
∴==.
