8.6 三角形内角和定理同步练习(含答案)
文档属性
| 名称 | 8.6 三角形内角和定理同步练习(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-22 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第八章 平行线的有关证明
6 三角形的内角和定理
知识能力全练
知识点一 三角形内角和定理
1.△ABC中,∠A=∠B=∠C,则此三角形为( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
2.如图所示,在△ABC中,∠A=60°,∠C=70°,BD平分∠ABC,DE∥BC,则∠BDE的度数是( )
A.50° B.25° C.30° D.35°
3.在下列条件中:①∠A+∠B=∠C;②∠A:∠B:∠C=1:2:3;③∠A=∠B==∠C;④∠A=∠B=2∠C;⑤∠A=∠B=∠C,能确定△ABC为直角三角形的条件有( )
A.2个 B.3个 C.4个 D.5个
4.如图所示,一束光线照射到平面镜AB上,然后在平面镜AB和CD之间来回反射,这时光线的反射角等于入射角,则∠1=∠2,∠3=∠4,∠5=∠6,若∠1=50°,∠6=65°,则∠3的度数为_____________.
5.如图所示,在△ABC中,BD⊥AC于点D,CE平分∠ACB交AB于点E,∠A=65°,∠CBD=36°,求∠BEC的度数.
知识点二 三角形的外角
6.如图所示,下列选项中的角是△BCD的外角的是( )
A.∠ACD B.∠DCE C.∠DAC D.∠D
知识点三 三角形的外角的有关定理
7.如图所示,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠ECD等于( )
A.40° B.45° C.50° D.55°
8.如图所示,D是△ABC中AC边上的一点,E是BD上一点,则对∠1,∠2,∠A之间的大小关系描述正确的是( )
A.∠A<∠1<∠2 B.∠2<∠1<∠A C.∠1>∠2>∠A D.无法确定
9.如图所示,在△ABC中,∠B=32°,将△ABC沿直线m翻折,点B落在点D的位置,则∠1-∠2的度数是__________度.
10.把一副三角板按如图所示的方式摆放,其中∠C=∠E=90°,∠A=45°,∠F=30°,则∠1+∠2=__________°.
11.已知,如图所示,点D、E分别在AB、AC边上,DE∥BC,F是AD上一点,FE的延长线交BC的延长线于点G.求证:
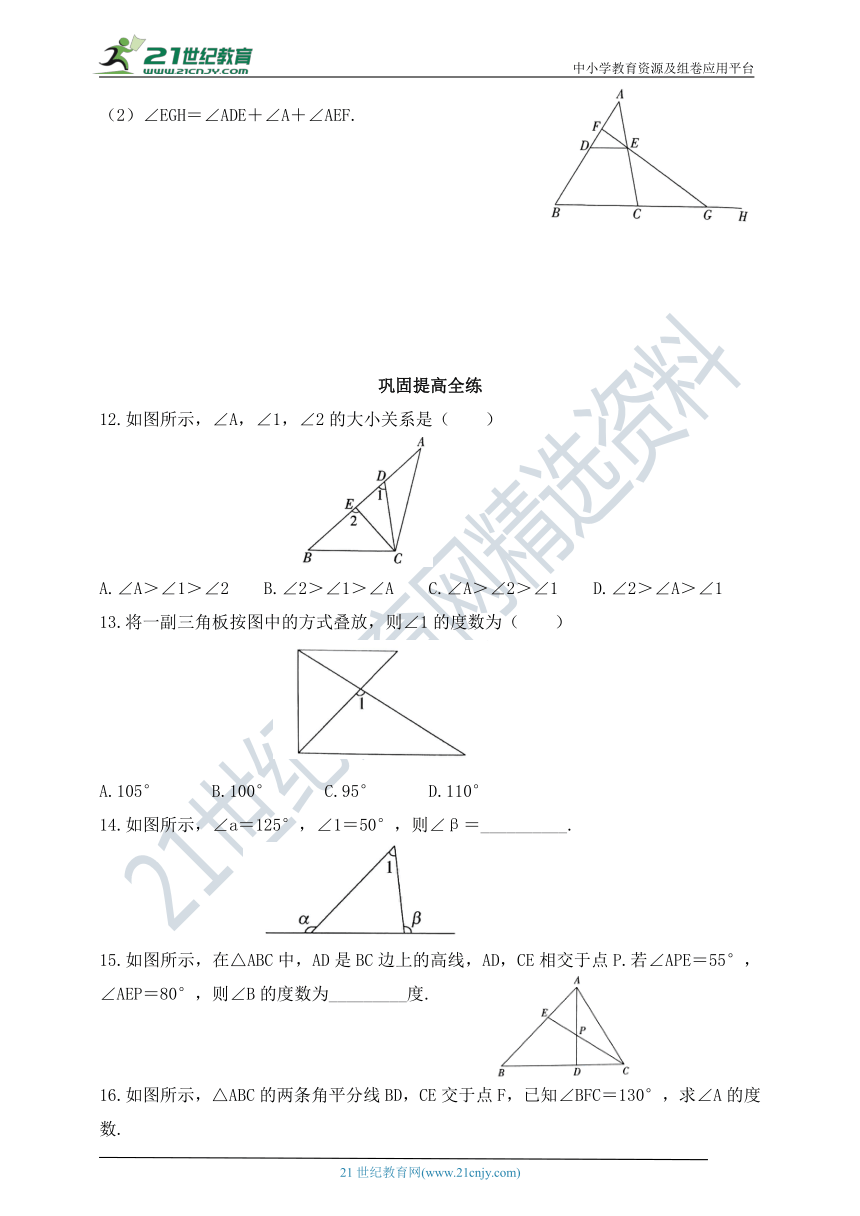
(1)∠EGH>∠ADE;
(2)∠EGH=∠ADE+∠A+∠AEF.
巩固提高全练
12.如图所示,∠A,∠1,∠2的大小关系是( )
A.∠A>∠1>∠2 B.∠2>∠1>∠A C.∠A>∠2>∠1 D.∠2>∠A>∠1
13.将一副三角板按图中的方式叠放,则∠1的度数为( )
A.105° B.100° C.95° D.110°
14.如图所示,∠a=125°,∠1=50°,则∠β=__________.
15.如图所示,在△ABC中,AD是BC边上的高线,AD,CE相交于点P.若∠APE=55°,∠AEP=80°,则∠B的度数为_________度.
16.如图所示,△ABC的两条角平分线BD,CE交于点F,已知∠BFC=130°,求∠A的度数.
17.如图所示,∠ACD是△ABC的外角,CE∥AB.若∠ACB=75°,∠ECD=50°,则∠A的度数为( )
A.50° B.55° C.70° D.75°
18.在△ABC中,若一个内角等于另外两个内角的差,则( )
A.必有一个内角等于30° B.必有一个内角等于45°
C.必有一个内角等于60° D.必有一个内角等于90°
19.将一副直角三角板按如图所示的方式放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上,则∠a的度数是( )
A.45° B.60° C.75° D.85
20.如图所示,将分别含有30°、45°角的一副三角板重叠,使直角顶点重合,若两直角重叠形成的角为65°,则图中∠a的度数为__________.
21.已知:如图所示,△ABC是任意一个三角形,求证:∠A+∠B+∠C=180°.
22.如图所示,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的平分线,CA2是∠A1CD的平分线,BA3是∠A2BD的平分线,CA3是∠A2CD的平分线,若∠A1=a,则
∠A2021=__________.
23.如图所示,在△ABC中,BD、CD分别是∠ABC、∠ACB的平分线,BP、CP分别
是△ABC的两个外角的平分线.
(1)当∠A=40°时,分别求∠D和∠P的度数;
(2)当∠A的大小变化时,试探究∠D+∠P的度数是否变化,如果不变化,求出∠D+∠P的值;如果变化,请说明理由.
参考答案
1.B 2.B 3.C
4.答案 57.5°
解析 如图,∵∠2=∠1=50°,∠5=∠6=65°,
∴∠7=180°-∠2-∠5=65°,∴∠3+∠4=180°-65°=115°
∵∠3=∠4,∴∠3=×115°=57.5°.
5.解析 ∵BD⊥AC,∠CBD=36°,∴∠BCD=90°-∠CBD=90°-36°=54°,
∵CE平分∠ACB,∴∠ACE=∠ACB=×54°=27°,
∵∠A=65°,∠A+∠AEC+∠ACE=180°,
∴∠AEC=180°-∠A-∠ACE=180°-65°-27°=88°,
∵∠AEC+∠BEC=180°,∴∠BEC=180°-∠AEC=180°-88°=92°.
6.B 7.C 8.A
9.答案 64
解析 如图所示:
由折叠的性质,得∠D=∠B=32°,
根据三角形外角的性质,得∠1=∠3+∠B,∠3=∠2+∠D,
∴∠1=∠2+∠D+∠B=∠2+2∠B=∠2+64°,
∴∠1-∠2=64°.
10.答案 225
解析 如图,
∵∠C=∠E=90°,∠A=45°,∠F=30°,∴∠D=60°,
∵∠1=∠D+∠3,∠2=∠F+∠6,∠3=∠4,∠5=∠6,∠4+∠5=180°-∠A,
∴∠1+∠2=∠D+∠F+∠4+∠5=∠D+∠F+180°-∠A
=60°+30°+180°-45°=225°.
11.证明 (1)∠EGH是△的外角,∴∠EGH>∠B
又∵DE∥BC,∴∠B=∠ADE,∴∠EGH>∠ADE.
(2)∵∠BFE是△AFE的外角,∴∠BFE=∠A+∠AEF.
∵∠EGH是△BFG的外角,∴∠EGH=∠B+∠BFE,∴∠EG=∠B+∠A+∠AEF,
又∵DE∥BC,∴∠B=∠ADE,∴∠EGH=∠ADE+∠A+∠AEF.
12.B 13.A
14.答案 105°
解析 ∵∠2=∠a-∠1=125°-50°=75°,
∴∠B=180°-∠2=180°-75°=105°.
15.答案 45
解析 ∵AD⊥BC,∴∠PDC=90°,
∵∠CPD=∠APE=55°,∴∠PCD=90°-55°=35°,
∵∠AEP=∠B+∠ECB,∴∠B=∠AEP-∠ECB=80°-35°=45°.
16.解析 BD平分∠ABC,CE平分∠ACB,
∴∠ABC=2∠FBC,∠ACB=2∠FCB,
∴∠ABC+∠ACB=2(∠FBC+∠FCB),
∵∠FBC+∠FCB=180°-∠BFC=180°-130°=50°,
∴∠ABC+∠ACB=2×50°=100°,
∴∠A=180°-(∠ABC+∠ACB)=180°-100°=80°.
17.B 18.D 19.C
20.答案 140°
解析 如图,
∵∠ACB=90°,∠DCB=65°,∴∠ACD=∠ACB-∠DCB=90°-65°=25°,
∵∠A=60°,∴∠DFB=∠AFC=180°-∠ACD-∠A=180°-25°-60°=95°,
∵∠D=45°,∴∠a=∠D+∠DFB=45°+95°=140°.
21.证明 如图,过点A作EF∥BC,
∵EF∥BC,∴∠1=∠B,∠2=∠C,
∵∠1+∠2+∠BAC=180°,∴∠BAC+∠B+∠C=180°.
22.答案
解析 ∵BA1是∠ABC的平分线,CA1是∠ACD的平分线,
∴∠A1BC=∠ABC,∠A1CD=∠ACD,
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,
∴(∠A+∠ABC)=∠ABC+∠A1,∴∠A1=∠A.
同理可得当∠A1=a时,
∠A2=∠A1=a,∠A3=∠A2=a,∠A4=∠A3=a,……,
∠A2021=.
23.解析(1)在△ABC中,∠ABC+∠ACB=180°-∠A,
∵BD、CD分别是∠ABC、∠ACB的平分线,∴∠DBC=∠ABC,∠DCB=∠ACB,
∴∠DBC+∠DCB=(∠ABC+∠ACB)=(180°-∠A)=90°-∠A,
在△BCD中,∠BDC=180°-(∠DBC+∠DCB)-=180°-(90°-∠A=90°+∠A,
当∠A=40°时,∠BDC=90°+20°=110°.
∵BP、CP分别是△ABC的两个外角的平分线,
∴∠CBP=∠CBE,∠BCP=∠BCF,
∴∠CBP+∠BCP=∠CBE+∠BCF=(∠CBE+∠BCF)
=(∠A+∠ACB+∠A+∠ABC)=(180°+∠A),
∴∠BPC=180°-(∠CBP+∠BCP)=180°-(180°+∠A)=90°-∠A,
当∠A=40°时,∠BPC=90°-×40°=70°.
(2)∠D+∠P的值不变.
由(1)知∠D=90°+∠A,∠P=90°-∠A,
∴∠D+∠P=180°.
_21?????????è?????(www.21cnjy.com)_
第八章 平行线的有关证明
6 三角形的内角和定理
知识能力全练
知识点一 三角形内角和定理
1.△ABC中,∠A=∠B=∠C,则此三角形为( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
2.如图所示,在△ABC中,∠A=60°,∠C=70°,BD平分∠ABC,DE∥BC,则∠BDE的度数是( )
A.50° B.25° C.30° D.35°
3.在下列条件中:①∠A+∠B=∠C;②∠A:∠B:∠C=1:2:3;③∠A=∠B==∠C;④∠A=∠B=2∠C;⑤∠A=∠B=∠C,能确定△ABC为直角三角形的条件有( )
A.2个 B.3个 C.4个 D.5个
4.如图所示,一束光线照射到平面镜AB上,然后在平面镜AB和CD之间来回反射,这时光线的反射角等于入射角,则∠1=∠2,∠3=∠4,∠5=∠6,若∠1=50°,∠6=65°,则∠3的度数为_____________.
5.如图所示,在△ABC中,BD⊥AC于点D,CE平分∠ACB交AB于点E,∠A=65°,∠CBD=36°,求∠BEC的度数.
知识点二 三角形的外角
6.如图所示,下列选项中的角是△BCD的外角的是( )
A.∠ACD B.∠DCE C.∠DAC D.∠D
知识点三 三角形的外角的有关定理
7.如图所示,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠ECD等于( )
A.40° B.45° C.50° D.55°
8.如图所示,D是△ABC中AC边上的一点,E是BD上一点,则对∠1,∠2,∠A之间的大小关系描述正确的是( )
A.∠A<∠1<∠2 B.∠2<∠1<∠A C.∠1>∠2>∠A D.无法确定
9.如图所示,在△ABC中,∠B=32°,将△ABC沿直线m翻折,点B落在点D的位置,则∠1-∠2的度数是__________度.
10.把一副三角板按如图所示的方式摆放,其中∠C=∠E=90°,∠A=45°,∠F=30°,则∠1+∠2=__________°.
11.已知,如图所示,点D、E分别在AB、AC边上,DE∥BC,F是AD上一点,FE的延长线交BC的延长线于点G.求证:
(1)∠EGH>∠ADE;
(2)∠EGH=∠ADE+∠A+∠AEF.
巩固提高全练
12.如图所示,∠A,∠1,∠2的大小关系是( )
A.∠A>∠1>∠2 B.∠2>∠1>∠A C.∠A>∠2>∠1 D.∠2>∠A>∠1
13.将一副三角板按图中的方式叠放,则∠1的度数为( )
A.105° B.100° C.95° D.110°
14.如图所示,∠a=125°,∠1=50°,则∠β=__________.
15.如图所示,在△ABC中,AD是BC边上的高线,AD,CE相交于点P.若∠APE=55°,∠AEP=80°,则∠B的度数为_________度.
16.如图所示,△ABC的两条角平分线BD,CE交于点F,已知∠BFC=130°,求∠A的度数.
17.如图所示,∠ACD是△ABC的外角,CE∥AB.若∠ACB=75°,∠ECD=50°,则∠A的度数为( )
A.50° B.55° C.70° D.75°
18.在△ABC中,若一个内角等于另外两个内角的差,则( )
A.必有一个内角等于30° B.必有一个内角等于45°
C.必有一个内角等于60° D.必有一个内角等于90°
19.将一副直角三角板按如图所示的方式放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上,则∠a的度数是( )
A.45° B.60° C.75° D.85
20.如图所示,将分别含有30°、45°角的一副三角板重叠,使直角顶点重合,若两直角重叠形成的角为65°,则图中∠a的度数为__________.
21.已知:如图所示,△ABC是任意一个三角形,求证:∠A+∠B+∠C=180°.
22.如图所示,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的平分线,CA2是∠A1CD的平分线,BA3是∠A2BD的平分线,CA3是∠A2CD的平分线,若∠A1=a,则
∠A2021=__________.
23.如图所示,在△ABC中,BD、CD分别是∠ABC、∠ACB的平分线,BP、CP分别
是△ABC的两个外角的平分线.
(1)当∠A=40°时,分别求∠D和∠P的度数;
(2)当∠A的大小变化时,试探究∠D+∠P的度数是否变化,如果不变化,求出∠D+∠P的值;如果变化,请说明理由.
参考答案
1.B 2.B 3.C
4.答案 57.5°
解析 如图,∵∠2=∠1=50°,∠5=∠6=65°,
∴∠7=180°-∠2-∠5=65°,∴∠3+∠4=180°-65°=115°
∵∠3=∠4,∴∠3=×115°=57.5°.
5.解析 ∵BD⊥AC,∠CBD=36°,∴∠BCD=90°-∠CBD=90°-36°=54°,
∵CE平分∠ACB,∴∠ACE=∠ACB=×54°=27°,
∵∠A=65°,∠A+∠AEC+∠ACE=180°,
∴∠AEC=180°-∠A-∠ACE=180°-65°-27°=88°,
∵∠AEC+∠BEC=180°,∴∠BEC=180°-∠AEC=180°-88°=92°.
6.B 7.C 8.A
9.答案 64
解析 如图所示:
由折叠的性质,得∠D=∠B=32°,
根据三角形外角的性质,得∠1=∠3+∠B,∠3=∠2+∠D,
∴∠1=∠2+∠D+∠B=∠2+2∠B=∠2+64°,
∴∠1-∠2=64°.
10.答案 225
解析 如图,
∵∠C=∠E=90°,∠A=45°,∠F=30°,∴∠D=60°,
∵∠1=∠D+∠3,∠2=∠F+∠6,∠3=∠4,∠5=∠6,∠4+∠5=180°-∠A,
∴∠1+∠2=∠D+∠F+∠4+∠5=∠D+∠F+180°-∠A
=60°+30°+180°-45°=225°.
11.证明 (1)∠EGH是△的外角,∴∠EGH>∠B
又∵DE∥BC,∴∠B=∠ADE,∴∠EGH>∠ADE.
(2)∵∠BFE是△AFE的外角,∴∠BFE=∠A+∠AEF.
∵∠EGH是△BFG的外角,∴∠EGH=∠B+∠BFE,∴∠EG=∠B+∠A+∠AEF,
又∵DE∥BC,∴∠B=∠ADE,∴∠EGH=∠ADE+∠A+∠AEF.
12.B 13.A
14.答案 105°
解析 ∵∠2=∠a-∠1=125°-50°=75°,
∴∠B=180°-∠2=180°-75°=105°.
15.答案 45
解析 ∵AD⊥BC,∴∠PDC=90°,
∵∠CPD=∠APE=55°,∴∠PCD=90°-55°=35°,
∵∠AEP=∠B+∠ECB,∴∠B=∠AEP-∠ECB=80°-35°=45°.
16.解析 BD平分∠ABC,CE平分∠ACB,
∴∠ABC=2∠FBC,∠ACB=2∠FCB,
∴∠ABC+∠ACB=2(∠FBC+∠FCB),
∵∠FBC+∠FCB=180°-∠BFC=180°-130°=50°,
∴∠ABC+∠ACB=2×50°=100°,
∴∠A=180°-(∠ABC+∠ACB)=180°-100°=80°.
17.B 18.D 19.C
20.答案 140°
解析 如图,
∵∠ACB=90°,∠DCB=65°,∴∠ACD=∠ACB-∠DCB=90°-65°=25°,
∵∠A=60°,∴∠DFB=∠AFC=180°-∠ACD-∠A=180°-25°-60°=95°,
∵∠D=45°,∴∠a=∠D+∠DFB=45°+95°=140°.
21.证明 如图,过点A作EF∥BC,
∵EF∥BC,∴∠1=∠B,∠2=∠C,
∵∠1+∠2+∠BAC=180°,∴∠BAC+∠B+∠C=180°.
22.答案
解析 ∵BA1是∠ABC的平分线,CA1是∠ACD的平分线,
∴∠A1BC=∠ABC,∠A1CD=∠ACD,
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,
∴(∠A+∠ABC)=∠ABC+∠A1,∴∠A1=∠A.
同理可得当∠A1=a时,
∠A2=∠A1=a,∠A3=∠A2=a,∠A4=∠A3=a,……,
∠A2021=.
23.解析(1)在△ABC中,∠ABC+∠ACB=180°-∠A,
∵BD、CD分别是∠ABC、∠ACB的平分线,∴∠DBC=∠ABC,∠DCB=∠ACB,
∴∠DBC+∠DCB=(∠ABC+∠ACB)=(180°-∠A)=90°-∠A,
在△BCD中,∠BDC=180°-(∠DBC+∠DCB)-=180°-(90°-∠A=90°+∠A,
当∠A=40°时,∠BDC=90°+20°=110°.
∵BP、CP分别是△ABC的两个外角的平分线,
∴∠CBP=∠CBE,∠BCP=∠BCF,
∴∠CBP+∠BCP=∠CBE+∠BCF=(∠CBE+∠BCF)
=(∠A+∠ACB+∠A+∠ABC)=(180°+∠A),
∴∠BPC=180°-(∠CBP+∠BCP)=180°-(180°+∠A)=90°-∠A,
当∠A=40°时,∠BPC=90°-×40°=70°.
(2)∠D+∠P的值不变.
由(1)知∠D=90°+∠A,∠P=90°-∠A,
∴∠D+∠P=180°.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
