8.6 三角形内角和定理课件(共20张PPT)
文档属性
| 名称 | 8.6 三角形内角和定理课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-22 17:10:35 | ||
图片预览



文档简介
第八章 平行线的有关证明
6 三角形内角和定理
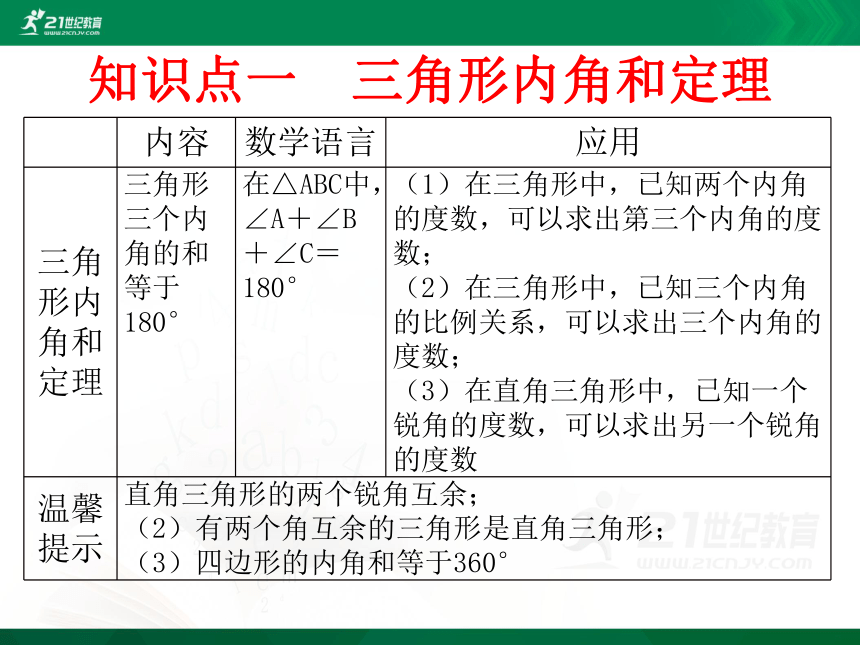
知识点一 三角形内角和定理
内容
数学语言
应用
三角形内角和定理
温馨提示
知识点一 三角形内角和定理
内容
数学语言
应用
三角形内角和定理
三角形三个内角的和等于180°
在△ABC中,∠A+∠B+∠C=180°
(1)在三角形中,已知两个内角的度数,可以求出第三个内角的度数;
(2)在三角形中,已知三个内角的比例关系,可以求出三个内角的度数;
(3)在直角三角形中,已知一个锐角的度数,可以求出另一个锐角的度数
温馨提示
直角三角形的两个锐角互余;
(2)有两个角互余的三角形是直角三角形;
(3)四边形的内角和等于360°
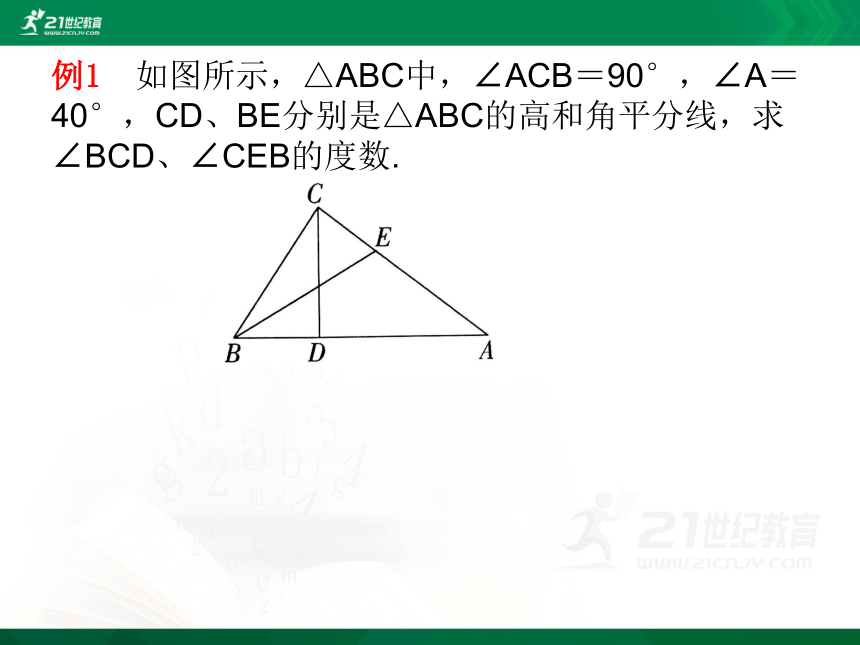
例1 如图所示,△ABC中,∠ACB=90°,∠A=40°,CD、BE分别是△ABC的高和角平分线,求∠BCD、∠CEB的度数.
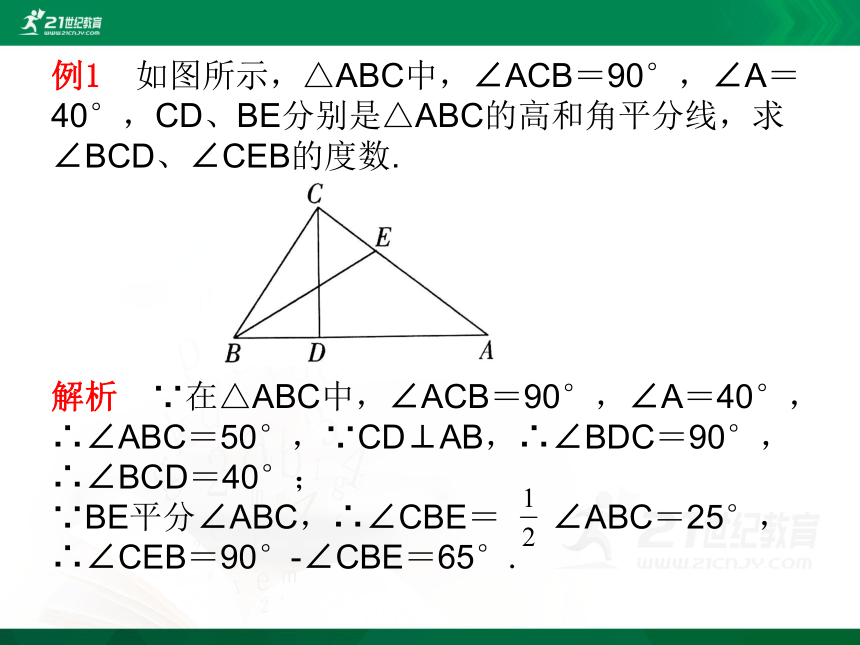
例1 如图所示,△ABC中,∠ACB=90°,∠A=40°,CD、BE分别是△ABC的高和角平分线,求∠BCD、∠CEB的度数.
解析 ∵在△ABC中,∠ACB=90°,∠A=40°,
∴∠ABC=50°,∵CD⊥AB,∴∠BDC=90°,
∴∠BCD=40°;
∵BE平分∠ABC,∴∠CBE= ∠ABC=25°,
∴∠CEB=90°-∠CBE=65°.
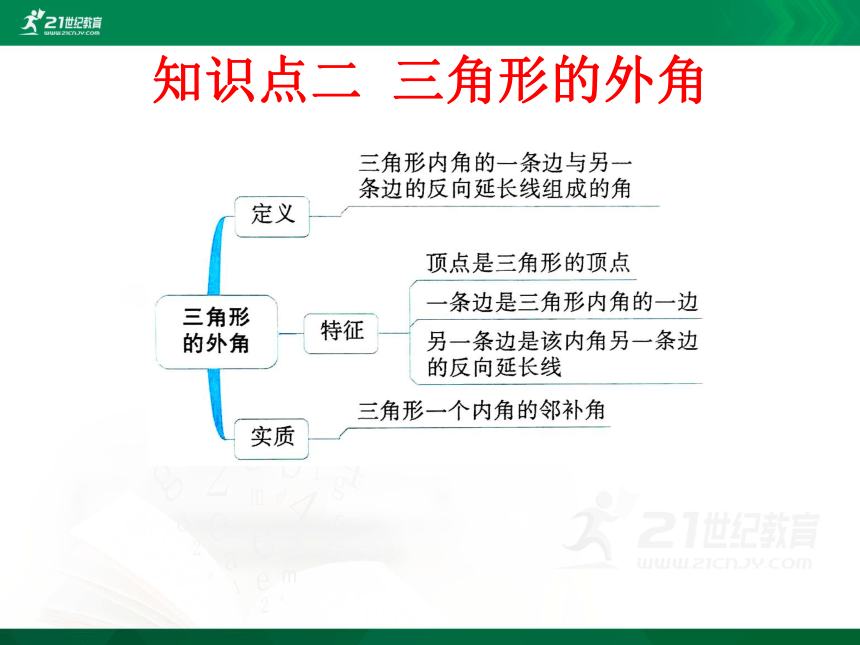
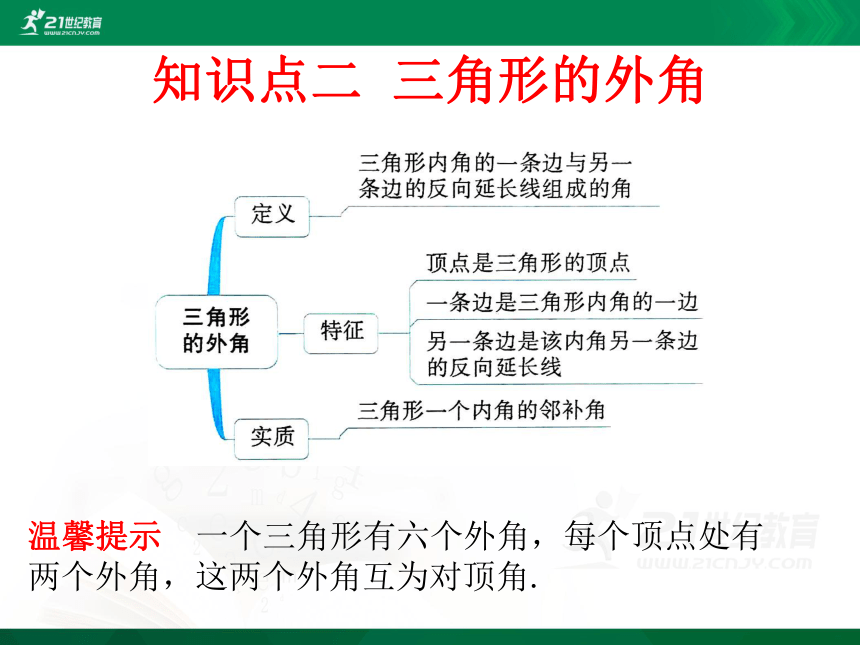
知识点二 三角形的外角
知识点二 三角形的外角
温馨提示 一个三角形有六个外角,每个顶点处有两个外角,这两个外角互为对顶角.
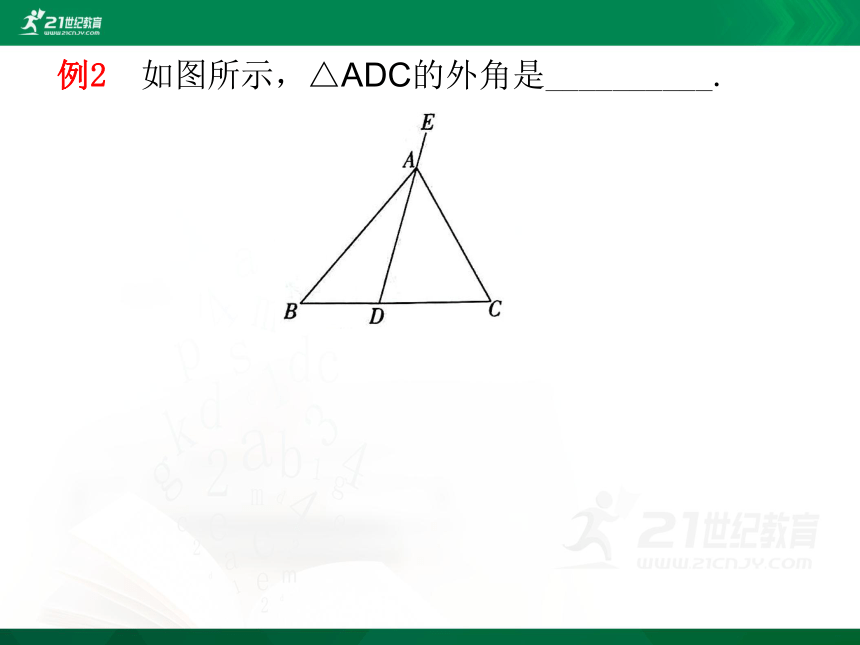
例2 如图所示,△ADC的外角是__________.
例2 如图所示,△ADC的外角是__________.
解析 根据三角形的外角的定义可知△ADC的外角为∠ADB,∠EAC.
答案 ∠ADB,∠EAC
知识点三 三角形的外角的有关定理
知识点三 三角形的外角的有关定理
温馨提示 (1)三角形外角的性质成立的条作是此外角与两个内角不相邻,如果与其他两个内角相邻就不成立,这是必须注意的条件.
(2)由一个基本事实或一个定理直接推出的命题,叫做这个基本事实或定理的推论,推论可以作为证明的依据.
例3 如图所示,根据标注的信息,求出a的大小.
.
例3 如图所示,根据标注的信息,求出a的大小.
解析 ∵α+15°=45°+180°-a,∴a=105°.
经典例题
题型一 三角形外角的性质的应用
例1 一个零件的形状如图所示,零件要求∠A必须等于90°,∠B和∠C分别为45°和35°,检验工人量得∠BDC=159°,就断定这个零件不合格,你知道为什么吗?
题型一 三角形外角的性质的应用
例1 一个零件的形状如图所示,零件要求∠A必须等于90°,∠B和∠C分别为45°和35°,检验工人量得∠BDC=159°,就断定这个零件不合格,你知道为什么吗?
解析 延长CD交AB于E,
∴∠BDC=∠B+∠DEB,∠DEB=∠C+∠A,
∵∠C=35°,∠B=45°,∠A=90°,
∴∠BDC=∠B+∠DEB=∠B+∠C+∠A=170°,
而量得∠BDC=159°,故这个零件不合格.
题型一 三角形外角的性质的应用
例1 一个零件的形状如图所示,零件要求∠A必须等于90°,∠B和∠C分别为45°和35°,检验工人量得∠BDC=159°,就断定这个零件不合格,你知道为什么吗?
解析 延长CD交AB于E,
∴∠BDC=∠B+∠DEB,∠DEB=∠C+∠A,
∵∠C=35°,∠B=45°,∠A=90°,
∴∠BDC=∠B+∠DEB=∠B+∠C+∠A=170°,
而量得∠BDC=159°,故这个零件不合格.
点拨 涉及三角形外角的计算问题,一般都可以利用三角形外角的性质并结合相关条件进行求解.
题型二 三角形内角和定理与三角形外角的性质的综合应用
例2 如图所示,在△ABC中,∠1=100°,∠C=80°,∠2=∠3,BE平分∠ABC.求∠4的度数.
题型二 三角形内角和定理与三角形外角的性质的综合应用
例2 如图所示,在△ABC中,∠1=100°,∠C=80°,∠2=∠3,BE平分∠ABC.求∠4的度数.
解析 ∵∠1=∠3+∠C,∠1=100°,C=80°,∴∠3=20°,∵∠2= ∠3,∴∠2=10°,
∴∠ABC=180°-80°-20°-10°=70°,
∵BE平分∠BAC,∴∠ABE=35°,
∵∠4=∠2+∠ABE,∴∠4=45°.
题型二 三角形内角和定理与三角形外角的性质的综合应用
例2 如图所示,在△ABC中,∠1=100°,∠C=80°,∠2=∠3,BE平分∠ABC.求∠4的度数.
解析 ∵∠1=∠3+∠C,∠1=100°,C=80°,∴∠3=20°,∵∠2= ∠3,∴∠2=10°,
∴∠ABC=180°-80°-20°-10°=70°,
∵BE平分∠BAC,∴∠ABE=35°,
∵∠4=∠2+∠ABE,∴∠4=45°.
点拨 综合应用三角形内角和定理与三角形外角的性质是解决此类问题的关键.
6 三角形内角和定理
知识点一 三角形内角和定理
内容
数学语言
应用
三角形内角和定理
温馨提示
知识点一 三角形内角和定理
内容
数学语言
应用
三角形内角和定理
三角形三个内角的和等于180°
在△ABC中,∠A+∠B+∠C=180°
(1)在三角形中,已知两个内角的度数,可以求出第三个内角的度数;
(2)在三角形中,已知三个内角的比例关系,可以求出三个内角的度数;
(3)在直角三角形中,已知一个锐角的度数,可以求出另一个锐角的度数
温馨提示
直角三角形的两个锐角互余;
(2)有两个角互余的三角形是直角三角形;
(3)四边形的内角和等于360°
例1 如图所示,△ABC中,∠ACB=90°,∠A=40°,CD、BE分别是△ABC的高和角平分线,求∠BCD、∠CEB的度数.
例1 如图所示,△ABC中,∠ACB=90°,∠A=40°,CD、BE分别是△ABC的高和角平分线,求∠BCD、∠CEB的度数.
解析 ∵在△ABC中,∠ACB=90°,∠A=40°,
∴∠ABC=50°,∵CD⊥AB,∴∠BDC=90°,
∴∠BCD=40°;
∵BE平分∠ABC,∴∠CBE= ∠ABC=25°,
∴∠CEB=90°-∠CBE=65°.
知识点二 三角形的外角
知识点二 三角形的外角
温馨提示 一个三角形有六个外角,每个顶点处有两个外角,这两个外角互为对顶角.
例2 如图所示,△ADC的外角是__________.
例2 如图所示,△ADC的外角是__________.
解析 根据三角形的外角的定义可知△ADC的外角为∠ADB,∠EAC.
答案 ∠ADB,∠EAC
知识点三 三角形的外角的有关定理
知识点三 三角形的外角的有关定理
温馨提示 (1)三角形外角的性质成立的条作是此外角与两个内角不相邻,如果与其他两个内角相邻就不成立,这是必须注意的条件.
(2)由一个基本事实或一个定理直接推出的命题,叫做这个基本事实或定理的推论,推论可以作为证明的依据.
例3 如图所示,根据标注的信息,求出a的大小.
.
例3 如图所示,根据标注的信息,求出a的大小.
解析 ∵α+15°=45°+180°-a,∴a=105°.
经典例题
题型一 三角形外角的性质的应用
例1 一个零件的形状如图所示,零件要求∠A必须等于90°,∠B和∠C分别为45°和35°,检验工人量得∠BDC=159°,就断定这个零件不合格,你知道为什么吗?
题型一 三角形外角的性质的应用
例1 一个零件的形状如图所示,零件要求∠A必须等于90°,∠B和∠C分别为45°和35°,检验工人量得∠BDC=159°,就断定这个零件不合格,你知道为什么吗?
解析 延长CD交AB于E,
∴∠BDC=∠B+∠DEB,∠DEB=∠C+∠A,
∵∠C=35°,∠B=45°,∠A=90°,
∴∠BDC=∠B+∠DEB=∠B+∠C+∠A=170°,
而量得∠BDC=159°,故这个零件不合格.
题型一 三角形外角的性质的应用
例1 一个零件的形状如图所示,零件要求∠A必须等于90°,∠B和∠C分别为45°和35°,检验工人量得∠BDC=159°,就断定这个零件不合格,你知道为什么吗?
解析 延长CD交AB于E,
∴∠BDC=∠B+∠DEB,∠DEB=∠C+∠A,
∵∠C=35°,∠B=45°,∠A=90°,
∴∠BDC=∠B+∠DEB=∠B+∠C+∠A=170°,
而量得∠BDC=159°,故这个零件不合格.
点拨 涉及三角形外角的计算问题,一般都可以利用三角形外角的性质并结合相关条件进行求解.
题型二 三角形内角和定理与三角形外角的性质的综合应用
例2 如图所示,在△ABC中,∠1=100°,∠C=80°,∠2=∠3,BE平分∠ABC.求∠4的度数.
题型二 三角形内角和定理与三角形外角的性质的综合应用
例2 如图所示,在△ABC中,∠1=100°,∠C=80°,∠2=∠3,BE平分∠ABC.求∠4的度数.
解析 ∵∠1=∠3+∠C,∠1=100°,C=80°,∴∠3=20°,∵∠2= ∠3,∴∠2=10°,
∴∠ABC=180°-80°-20°-10°=70°,
∵BE平分∠BAC,∴∠ABE=35°,
∵∠4=∠2+∠ABE,∴∠4=45°.
题型二 三角形内角和定理与三角形外角的性质的综合应用
例2 如图所示,在△ABC中,∠1=100°,∠C=80°,∠2=∠3,BE平分∠ABC.求∠4的度数.
解析 ∵∠1=∠3+∠C,∠1=100°,C=80°,∴∠3=20°,∵∠2= ∠3,∴∠2=10°,
∴∠ABC=180°-80°-20°-10°=70°,
∵BE平分∠BAC,∴∠ABE=35°,
∵∠4=∠2+∠ABE,∴∠4=45°.
点拨 综合应用三角形内角和定理与三角形外角的性质是解决此类问题的关键.
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
