2020—2021学年人教版九年级数学下册第27章《相似》常考题型综合练习五( Word版 含答案)
文档属性
| 名称 | 2020—2021学年人教版九年级数学下册第27章《相似》常考题型综合练习五( Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 196.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-22 18:27:48 | ||
图片预览


文档简介
九年级数学下册第27章《相似》常考题型综合练习五
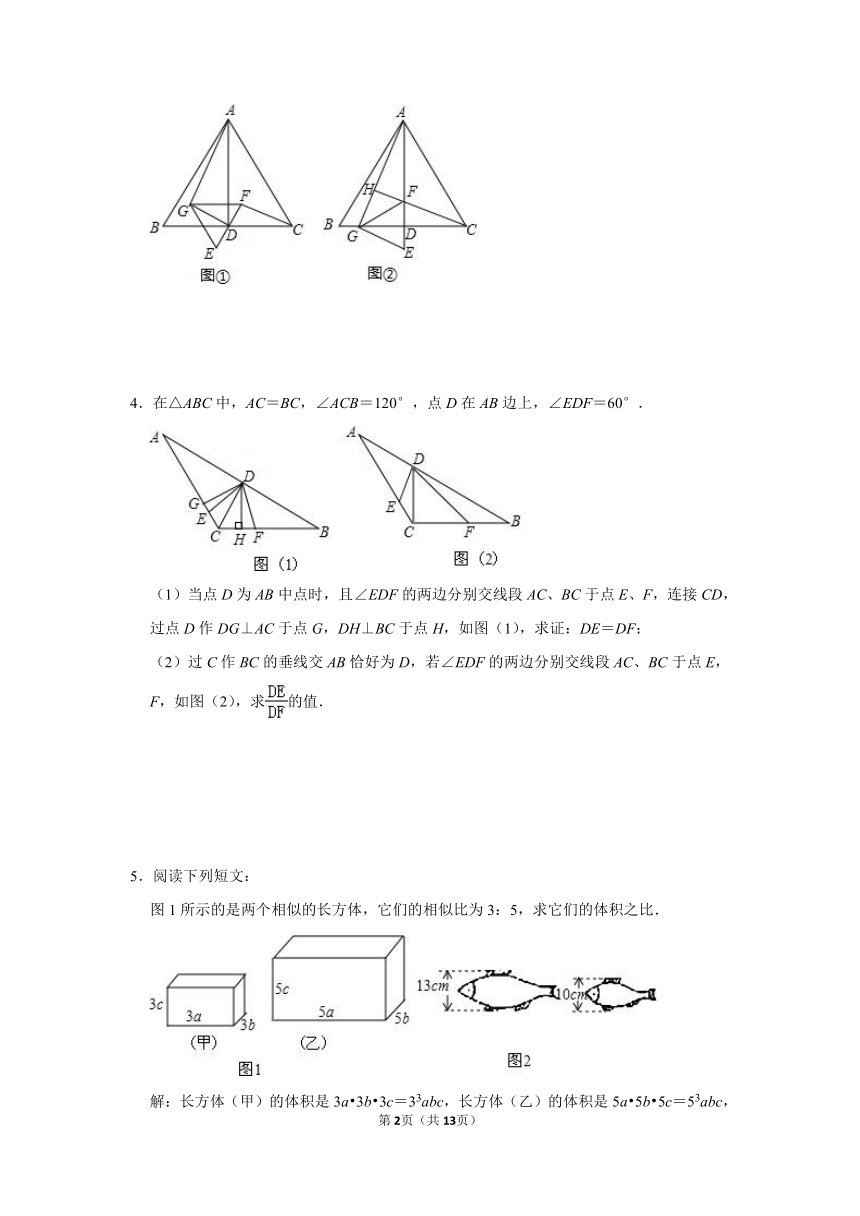
1.如图,在?ABCD中,O为对角线BD的中点,BE平分∠ABC且交AD于点P,交CD的延长线于点E;作EO交AD于点F,交BC于点G.
(1)求证:DF=BG;
(2)若AB=6,AD=9,求DF的长.
2.已知:如图,在△ABC中,点D为边BC上的点,=,∠BAD=∠CAE.
(1)求证:△BAC∽△DAE;
(2)当∠BAC=90°时,求证:EC⊥BC.
3.探究:如图①,△ABC是等边三角形,AD是BC边上的高线,以点D为中点作线段EF,且EF不与BC边重合,以EF为边作等边三角形EFG,连结AG,GD,CF.求证:△ADG∽△CDF;
应用:如图②,将线段EF绕着点D逆时针旋转,当点F落在AD上时,延长CF交AG于点H,求∠AHF的度数.
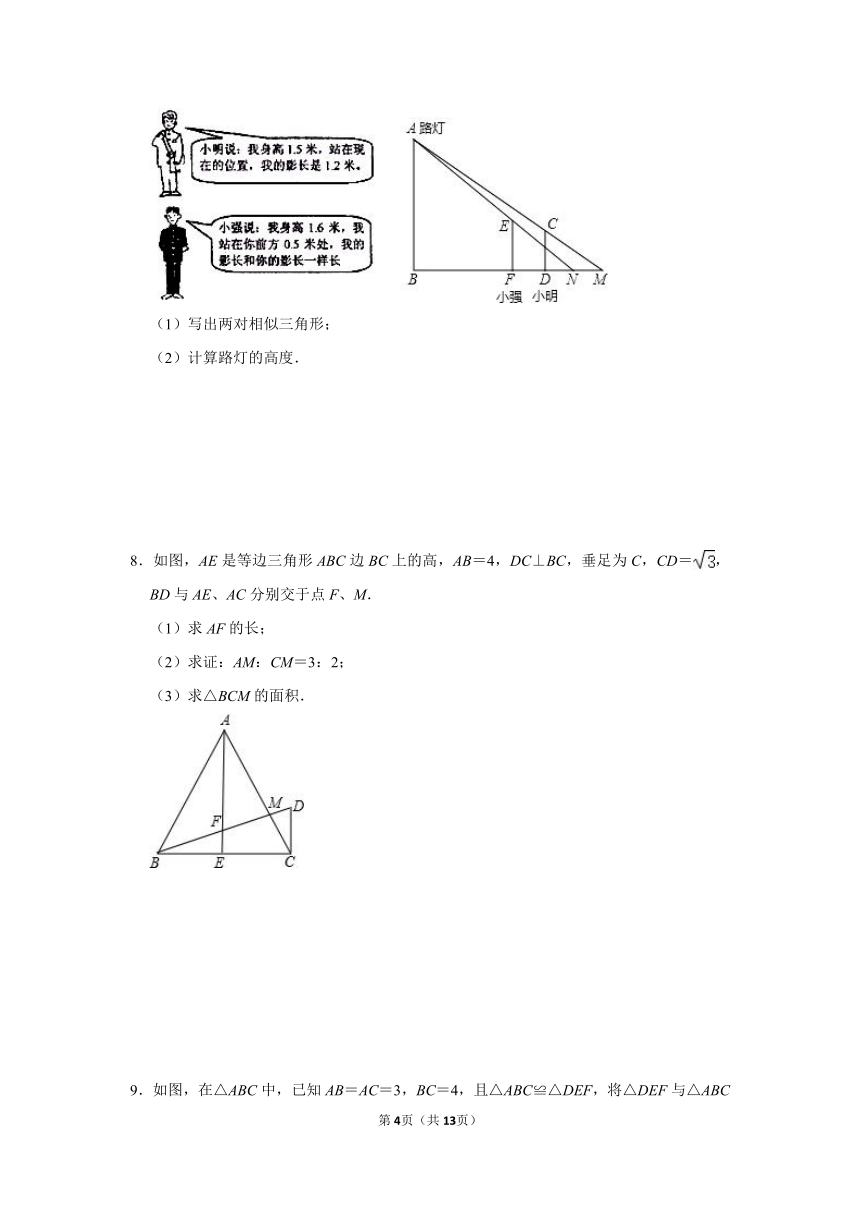
4.在△ABC中,AC=BC,∠ACB=120°,点D在AB边上,∠EDF=60°.
(1)当点D为AB中点时,且∠EDF的两边分别交线段AC、BC于点E、F,连接CD,过点D作DG⊥AC于点G,DH⊥BC于点H,如图(1),求证:DE=DF;
(2)过C作BC的垂线交AB恰好为D,若∠EDF的两边分别交线段AC、BC于点E,F,如图(2),求的值.
5.阅读下列短文:
图1所示的是两个相似的长方体,它们的相似比为3:5,求它们的体积之比.
解:长方体(甲)的体积是3a?3b?3c=33abc,长方体(乙)的体积是5a?5b?5c=53abc,所以长方体(甲)与长方体(乙)的体积的比是33abc:53abc=33:53=(3:5)3,所以,相似形的体积之比,等于它的相似比的立方.
请仿上例解答下题:
鱼是一种高蛋白食物,所以谁都希望买到价廉物美的鱼.假定现在市场上出售同一种鱼(体形是相似形),以大小论价,大鱼A每斤1.5元,小鱼B每斤1元.如果大鱼的高度为13厘米,小鱼的高度为10厘米(图2所示),那么买哪种鱼更便宜呢?
6.如图,已知∠BAC=90°,AD⊥BC于D,E是AC的中点,ED的延长线交AB的延长线于点F.求证:
(1)△DFB∽△AFD;
(2)AB:AC=DF:AF.
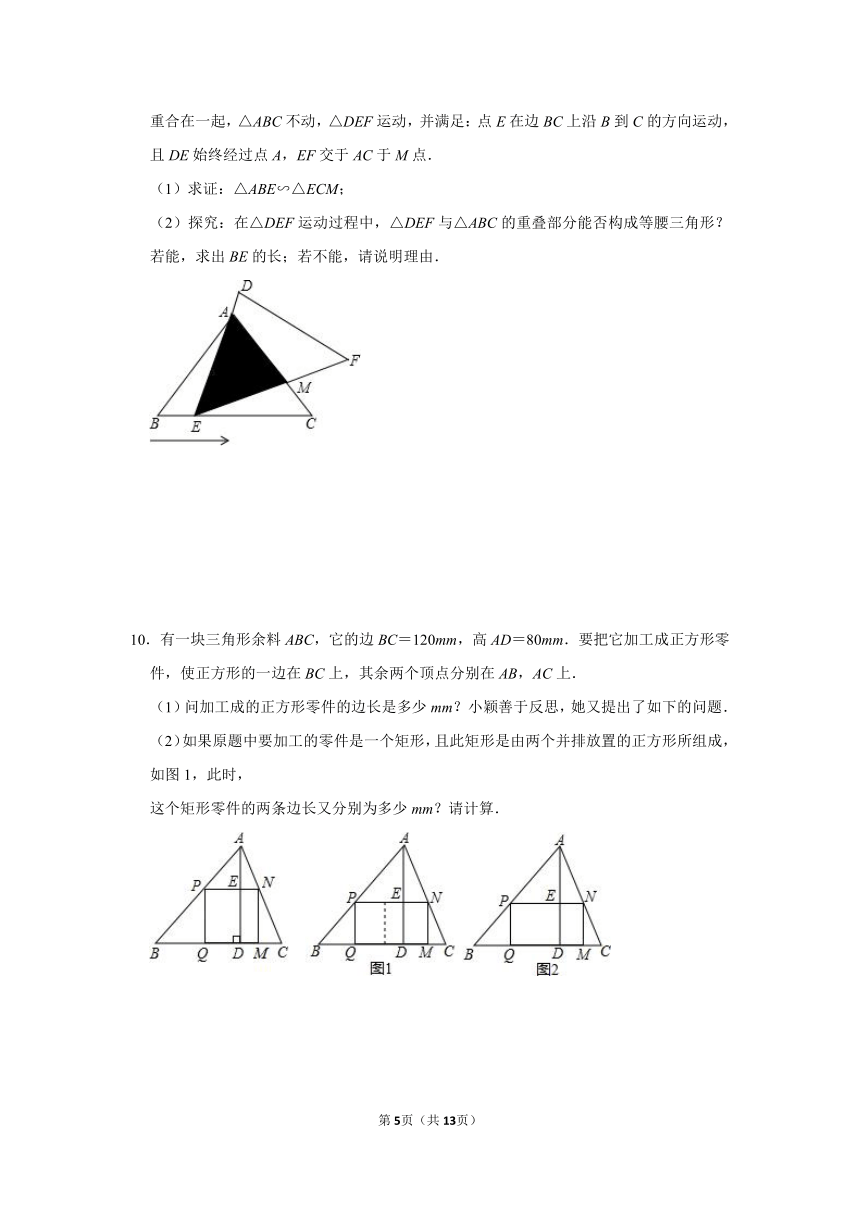
7.小明和小强晚上在路灯下朝着路灯的方向行走(小明、小强和路灯在同一条直线上)从下面两人的对话中请你计算出路灯的高度.
(1)写出两对相似三角形;
(2)计算路灯的高度.
8.如图,AE是等边三角形ABC边BC上的高,AB=4,DC⊥BC,垂足为C,CD=,BD与AE、AC分别交于点F、M.
(1)求AF的长;
(2)求证:AM:CM=3:2;
(3)求△BCM的面积.
9.如图,在△ABC中,已知AB=AC=3,BC=4,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF交于AC于M点.
(1)求证:△ABE∽△ECM;
(2)探究:在△DEF运动过程中,△DEF与△ABC的重叠部分能否构成等腰三角形?若能,求出BE的长;若不能,请说明理由.
10.有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)问加工成的正方形零件的边长是多少mm?小颖善于反思,她又提出了如下的问题.
(2)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,
这个矩形零件的两条边长又分别为多少mm?请计算.
参考答案
1.(1)证明:连接FB、DG,
∵四边形ABCD是平行四边形,
∴AD∥CD,又BO=OD,
∴GO=OF,
∴四边形FBGD是平行四边形,
∴DF=BG;
(2)∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵AD∥BC,
∴∠APB=∠EBC,
∴∠ABE=∠APB,
∴AP=AB=6,
∴PD=9﹣6=3,
∵AD∥BC,PD=3,BC=9,
∴=,又BG=DF,
∴PF=DF,又PD=3,
∴DF=.
2.(1)证明:∵∠BAD=∠CAE,
∴∠BAD+∠DAC=∠DAC+∠CAE,即∠DAE,
∵=,
∴=,
∴△BAC∽△DAE;
(2)解:∵△BAC∽△DAE,
∴∠B=∠ACE,
∵∠BAC=90°,
∴∠B+∠ACB=90°,
∴∠ACB+∠ACB=90°,即∠BCE=90°,
∴EC⊥BC.
3.解:探究:如图①∵△EFG是等边三角形,D是EF的中点,
∴GD⊥EF,
∵AD⊥BC,
∴∠ADF+∠ADG=∠CDF+∠ADF,
∴∠ADG=∠CDF,
∵△ABC与△EFG是等边三角形,
∴△ABC∽△EFG,
∴,
∴△ADG∽△CDF;
应用:如图②,
∵△ADG∽△CDF,
∴∠GAD=∠FCD,
∵∠FDC=90°,∠AFH=∠CFD,
∴∠GAD+∠AFH=∠FCD+∠CFD=90°,
∴∠AHF=90°.
4.(1)证明:∵DG⊥AC,DH⊥BC,
∴∠DGE=∠DHF=90°,
∵AC=BC,点D为AB中点,
∴CD平分∠ACB,
∴DG=DH,
∵∠ACB=120°,∠EDF=60°,
∴∠DEC+∠DFH=180°,
∵∠DEC+∠DEG=180°,
∴∠DFH=∠DEG,
在△DGE与△DHF中,
,
∴△DGE≌△DHF,
∴DE=DF,
(2)∵CD⊥BC,
∴∠DCB=90°,
∵∠ACB=120°,AC=BC,
∴∠ACD=∠A=∠B=30°,
∴BD=2CD,∴∠BDC=60°,
∴∠BDF+∠CDF=60°,
∵∠EDF=60°,
∴∠CDF+CDE=60°,
∴∠CDE=∠BDF,
∴△CDE∽△BDF,
∴.
5.解:大鱼A与小鱼B相似比为13:10,
则大鱼A与小鱼B体积之比()3=2.197,
而其价格比是1.5:1=1.5,A的体积是B的2.197倍,买大鱼A比买小鱼B合算.
6.解:(1)∵∠BAC=90°,AD⊥BC于D,
∴∠BAC=∠ADB=90°,
∴∠BAD+∠ABD=∠ABD+∠C=90°,
∴∠BAD=∠C,
∵E是AC的中点,
∴DE=CE,
∴∠C=∠EDC,
∵∠EDC=∠BDF,
∴∠BAD=∠BDF,
∵∠F=∠F,
∴△DFB∽△AFD;
(2)∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∴∠BAD+∠DAC=90°,∠DAC+∠ACD=90°,
∴∠BAD=∠ACD,
∵∠ADB=∠ADC,
∴△ABD∽△CAD;
∴=,
∵△DFB∽△AFD;
∴,
∴AB:AC=DF:AF.
7.解:(1)△ABN~△EFN△ABM~△CDM;
(2)根据题意,MN=FD=0.5米,
∵△ABM∽△CDM,
∴=,即=﹣﹣﹣﹣﹣①,
∵△ABN∽△EFN,
∴=,即=﹣﹣﹣﹣﹣②,
①②两式联立解得AB=10.
故路灯的高度10米.
8.解:(1)∵△ABC是等边三角形,
∴AB=AC=BC=4,
∵AE⊥BC,
∴BE=BC=2,AE=2,
∵DC⊥BC,
∴CD∥AE,
∴EF=CD=,
∴AF=AE﹣EF=;
(2)∵AF∥CD,
∴△AFM∽△CDM,
∴,
由(1)知,AF=,CD=,
∴AM:CM=AF:CD=3:2;
(3)过M作MN⊥BC于N,
∴MN∥AE,
∴△CMN≌△CAE,
∴,
由(2)知AM:CM=3:2;
∴CM:AC=2:5,
∴MN=,
∴S△BCM=BC?MN==.
9.(1)证明:∵AB=AC,
∴∠B=∠C,
∵△ABC≌△DEF,
∴∠AEF=∠B,
又∵∠AEF+∠CEM=∠AEC=∠B+∠BAE,
∴∠CEM=∠BAE,
∴△ABE∽△ECM;
(2)能.
解:∵∠AEF=∠B=∠C,且∠AME>∠C,
∴∠AME>∠AEF,
∴AE≠AM;
当AE=EM时,则△ABE≌△ECM,
∴CE=AB=5,
∴BE=BC﹣EC=6﹣5=1,
当AM=EM时,则∠MAE=∠MEA,
∴∠MAE+∠BAE=∠MEA+∠CEM,
即∠CAB=∠CEA,
又∵∠C=∠C,
∴△CAE∽△CBA,
∴=,
∴CE==,
∴BE=4﹣=;
∴BE=1或.
10.解:(1)设正方形的边长为xmm,则PN=PQ=ED=x,
∴AE=AD﹣ED=80﹣x,
∵PN∥BC,
∴△APN∽△ABC,
∴=,即=,解得x=48,
∴加工成的正方形零件的边长是48mm;
(2)设PQ=x,则PN=2x,AE=80﹣x,
∵PN∥BC,
∴△APN∽△ABC,
∴=,即=,解得x=,
∴2x=,
∴这个矩形零件的两条边长分别为mm,
mm.
第1页(共1页)
1.如图,在?ABCD中,O为对角线BD的中点,BE平分∠ABC且交AD于点P,交CD的延长线于点E;作EO交AD于点F,交BC于点G.
(1)求证:DF=BG;
(2)若AB=6,AD=9,求DF的长.
2.已知:如图,在△ABC中,点D为边BC上的点,=,∠BAD=∠CAE.
(1)求证:△BAC∽△DAE;
(2)当∠BAC=90°时,求证:EC⊥BC.
3.探究:如图①,△ABC是等边三角形,AD是BC边上的高线,以点D为中点作线段EF,且EF不与BC边重合,以EF为边作等边三角形EFG,连结AG,GD,CF.求证:△ADG∽△CDF;
应用:如图②,将线段EF绕着点D逆时针旋转,当点F落在AD上时,延长CF交AG于点H,求∠AHF的度数.
4.在△ABC中,AC=BC,∠ACB=120°,点D在AB边上,∠EDF=60°.
(1)当点D为AB中点时,且∠EDF的两边分别交线段AC、BC于点E、F,连接CD,过点D作DG⊥AC于点G,DH⊥BC于点H,如图(1),求证:DE=DF;
(2)过C作BC的垂线交AB恰好为D,若∠EDF的两边分别交线段AC、BC于点E,F,如图(2),求的值.
5.阅读下列短文:
图1所示的是两个相似的长方体,它们的相似比为3:5,求它们的体积之比.
解:长方体(甲)的体积是3a?3b?3c=33abc,长方体(乙)的体积是5a?5b?5c=53abc,所以长方体(甲)与长方体(乙)的体积的比是33abc:53abc=33:53=(3:5)3,所以,相似形的体积之比,等于它的相似比的立方.
请仿上例解答下题:
鱼是一种高蛋白食物,所以谁都希望买到价廉物美的鱼.假定现在市场上出售同一种鱼(体形是相似形),以大小论价,大鱼A每斤1.5元,小鱼B每斤1元.如果大鱼的高度为13厘米,小鱼的高度为10厘米(图2所示),那么买哪种鱼更便宜呢?
6.如图,已知∠BAC=90°,AD⊥BC于D,E是AC的中点,ED的延长线交AB的延长线于点F.求证:
(1)△DFB∽△AFD;
(2)AB:AC=DF:AF.
7.小明和小强晚上在路灯下朝着路灯的方向行走(小明、小强和路灯在同一条直线上)从下面两人的对话中请你计算出路灯的高度.
(1)写出两对相似三角形;
(2)计算路灯的高度.
8.如图,AE是等边三角形ABC边BC上的高,AB=4,DC⊥BC,垂足为C,CD=,BD与AE、AC分别交于点F、M.
(1)求AF的长;
(2)求证:AM:CM=3:2;
(3)求△BCM的面积.
9.如图,在△ABC中,已知AB=AC=3,BC=4,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF交于AC于M点.
(1)求证:△ABE∽△ECM;
(2)探究:在△DEF运动过程中,△DEF与△ABC的重叠部分能否构成等腰三角形?若能,求出BE的长;若不能,请说明理由.
10.有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)问加工成的正方形零件的边长是多少mm?小颖善于反思,她又提出了如下的问题.
(2)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,
这个矩形零件的两条边长又分别为多少mm?请计算.
参考答案
1.(1)证明:连接FB、DG,
∵四边形ABCD是平行四边形,
∴AD∥CD,又BO=OD,
∴GO=OF,
∴四边形FBGD是平行四边形,
∴DF=BG;
(2)∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵AD∥BC,
∴∠APB=∠EBC,
∴∠ABE=∠APB,
∴AP=AB=6,
∴PD=9﹣6=3,
∵AD∥BC,PD=3,BC=9,
∴=,又BG=DF,
∴PF=DF,又PD=3,
∴DF=.
2.(1)证明:∵∠BAD=∠CAE,
∴∠BAD+∠DAC=∠DAC+∠CAE,即∠DAE,
∵=,
∴=,
∴△BAC∽△DAE;
(2)解:∵△BAC∽△DAE,
∴∠B=∠ACE,
∵∠BAC=90°,
∴∠B+∠ACB=90°,
∴∠ACB+∠ACB=90°,即∠BCE=90°,
∴EC⊥BC.
3.解:探究:如图①∵△EFG是等边三角形,D是EF的中点,
∴GD⊥EF,
∵AD⊥BC,
∴∠ADF+∠ADG=∠CDF+∠ADF,
∴∠ADG=∠CDF,
∵△ABC与△EFG是等边三角形,
∴△ABC∽△EFG,
∴,
∴△ADG∽△CDF;
应用:如图②,
∵△ADG∽△CDF,
∴∠GAD=∠FCD,
∵∠FDC=90°,∠AFH=∠CFD,
∴∠GAD+∠AFH=∠FCD+∠CFD=90°,
∴∠AHF=90°.
4.(1)证明:∵DG⊥AC,DH⊥BC,
∴∠DGE=∠DHF=90°,
∵AC=BC,点D为AB中点,
∴CD平分∠ACB,
∴DG=DH,
∵∠ACB=120°,∠EDF=60°,
∴∠DEC+∠DFH=180°,
∵∠DEC+∠DEG=180°,
∴∠DFH=∠DEG,
在△DGE与△DHF中,
,
∴△DGE≌△DHF,
∴DE=DF,
(2)∵CD⊥BC,
∴∠DCB=90°,
∵∠ACB=120°,AC=BC,
∴∠ACD=∠A=∠B=30°,
∴BD=2CD,∴∠BDC=60°,
∴∠BDF+∠CDF=60°,
∵∠EDF=60°,
∴∠CDF+CDE=60°,
∴∠CDE=∠BDF,
∴△CDE∽△BDF,
∴.
5.解:大鱼A与小鱼B相似比为13:10,
则大鱼A与小鱼B体积之比()3=2.197,
而其价格比是1.5:1=1.5,A的体积是B的2.197倍,买大鱼A比买小鱼B合算.
6.解:(1)∵∠BAC=90°,AD⊥BC于D,
∴∠BAC=∠ADB=90°,
∴∠BAD+∠ABD=∠ABD+∠C=90°,
∴∠BAD=∠C,
∵E是AC的中点,
∴DE=CE,
∴∠C=∠EDC,
∵∠EDC=∠BDF,
∴∠BAD=∠BDF,
∵∠F=∠F,
∴△DFB∽△AFD;
(2)∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∴∠BAD+∠DAC=90°,∠DAC+∠ACD=90°,
∴∠BAD=∠ACD,
∵∠ADB=∠ADC,
∴△ABD∽△CAD;
∴=,
∵△DFB∽△AFD;
∴,
∴AB:AC=DF:AF.
7.解:(1)△ABN~△EFN△ABM~△CDM;
(2)根据题意,MN=FD=0.5米,
∵△ABM∽△CDM,
∴=,即=﹣﹣﹣﹣﹣①,
∵△ABN∽△EFN,
∴=,即=﹣﹣﹣﹣﹣②,
①②两式联立解得AB=10.
故路灯的高度10米.
8.解:(1)∵△ABC是等边三角形,
∴AB=AC=BC=4,
∵AE⊥BC,
∴BE=BC=2,AE=2,
∵DC⊥BC,
∴CD∥AE,
∴EF=CD=,
∴AF=AE﹣EF=;
(2)∵AF∥CD,
∴△AFM∽△CDM,
∴,
由(1)知,AF=,CD=,
∴AM:CM=AF:CD=3:2;
(3)过M作MN⊥BC于N,
∴MN∥AE,
∴△CMN≌△CAE,
∴,
由(2)知AM:CM=3:2;
∴CM:AC=2:5,
∴MN=,
∴S△BCM=BC?MN==.
9.(1)证明:∵AB=AC,
∴∠B=∠C,
∵△ABC≌△DEF,
∴∠AEF=∠B,
又∵∠AEF+∠CEM=∠AEC=∠B+∠BAE,
∴∠CEM=∠BAE,
∴△ABE∽△ECM;
(2)能.
解:∵∠AEF=∠B=∠C,且∠AME>∠C,
∴∠AME>∠AEF,
∴AE≠AM;
当AE=EM时,则△ABE≌△ECM,
∴CE=AB=5,
∴BE=BC﹣EC=6﹣5=1,
当AM=EM时,则∠MAE=∠MEA,
∴∠MAE+∠BAE=∠MEA+∠CEM,
即∠CAB=∠CEA,
又∵∠C=∠C,
∴△CAE∽△CBA,
∴=,
∴CE==,
∴BE=4﹣=;
∴BE=1或.
10.解:(1)设正方形的边长为xmm,则PN=PQ=ED=x,
∴AE=AD﹣ED=80﹣x,
∵PN∥BC,
∴△APN∽△ABC,
∴=,即=,解得x=48,
∴加工成的正方形零件的边长是48mm;
(2)设PQ=x,则PN=2x,AE=80﹣x,
∵PN∥BC,
∴△APN∽△ABC,
∴=,即=,解得x=,
∴2x=,
∴这个矩形零件的两条边长分别为mm,
mm.
第1页(共1页)
