第27章相似 单元测试-2020-2021学年人教版九年级数学下册(Word版 含解析)
文档属性
| 名称 | 第27章相似 单元测试-2020-2021学年人教版九年级数学下册(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 309.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-22 00:00:00 | ||
图片预览



文档简介
第27章
《相似》
单
元
测
试
卷
题号
一
二
三
总分
得分
得
分
评卷人
一.单项选择题。(本大题共10小题,每小题4分,共40分。每小题只有一个正确答案,请将正确的答案的序号填入括号中。)
1.下列各组图形中,一定相似的是( )
A.任意两个圆
B.任意两个等腰三角形
C.任意两个菱形
D.任意两个矩形
2.如图,把矩形ABCD中的AB边向上翻折到AD边上,当点B与点F重合时,折痕与BC边交于点E,连接EF,若四边形EFDC与矩形ABCD恰好相似,若AB=1时,AD的长为( )
A.
B.
C.3
D.1
3.如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若,AD=6,则AB等于( )
A.8
B.6
C.4
D.2
4.已知△ABC∽△A′B′C′,AD和A′D′是对应高,且AD:A′D′=2,则它们的周长比是( )
A.1:2
B.2:1
C.1:4
D.4:1
5.如图,∠1=∠2,要使△ABC∽△ADE,只需要添加一个条件即可,这个条件不可能是( )
A.∠B=∠D
B.∠C=∠E
C.
D.
6.如图,在Rt△ABC中,按以下步骤作图:分别以B,C为圆心,以大于BC的长为半径作弧,弧线两两交于P、Q两点,作直线PQ,与边AB、BC分别交于D、E两点,连接CD、AE,AE、CD交于点F.在下列说法中:①∠ADC=2∠DCB;②AEBC;③AF?EF=DF?CF;④若AB=8,BC=10,则△ADC的周长为14.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
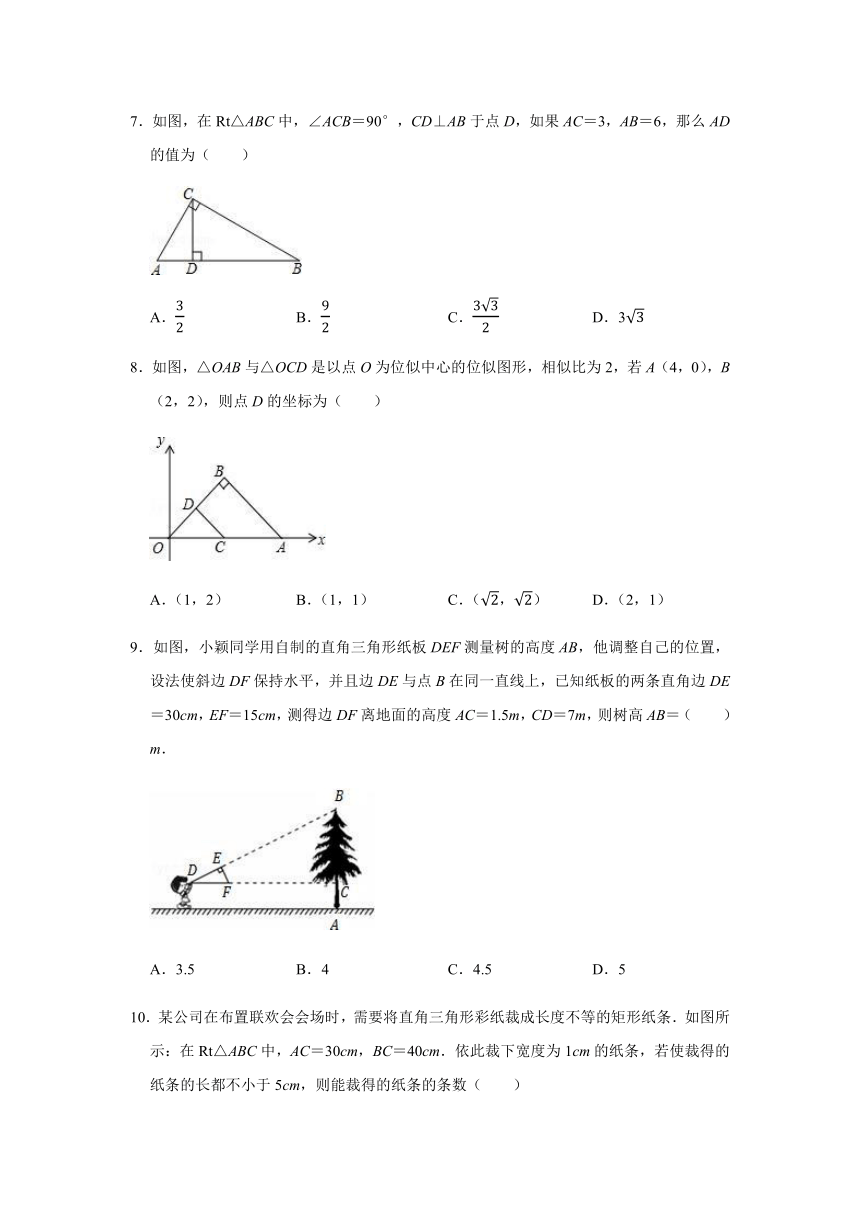
7.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,如果AC=3,AB=6,那么AD的值为( )
A.
B.
C.
D.3
8.如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为2,若A(4,0),B(2,2),则点D的坐标为( )
A.(1,2)
B.(1,1)
C.(,)
D.(2,1)
9.如图,小颖同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=30cm,EF=15cm,测得边DF离地面的高度AC=1.5m,CD=7m,则树高AB=( )m.
A.3.5
B.4
C.4.5
D.5
10.某公司在布置联欢会会场时,需要将直角三角形彩纸裁成长度不等的矩形纸条.如图所示:在Rt△ABC中,AC=30cm,BC=40cm.依此裁下宽度为1cm的纸条,若使裁得的纸条的长都不小于5cm,则能裁得的纸条的条数( )
A.24
B.25
C.26
D.27
得
分
评卷人
二、填空题(本大题共4小题,每小题5分,共20分。)
11.已知,那么
.
12.已知:△ABC中,D为BC的中点,E为AB上一点,且BEAB,F为AC上一点,且CFAC,EF交AD于P,则EP:PF=
.
13.在平面直角坐标系中,已知点E(﹣4,2),F(﹣2,﹣2).以原点O为位似中心,相似比为0.5,把△EFO缩小,得到△E'F'O,则点E的对应点E'的坐标是
.
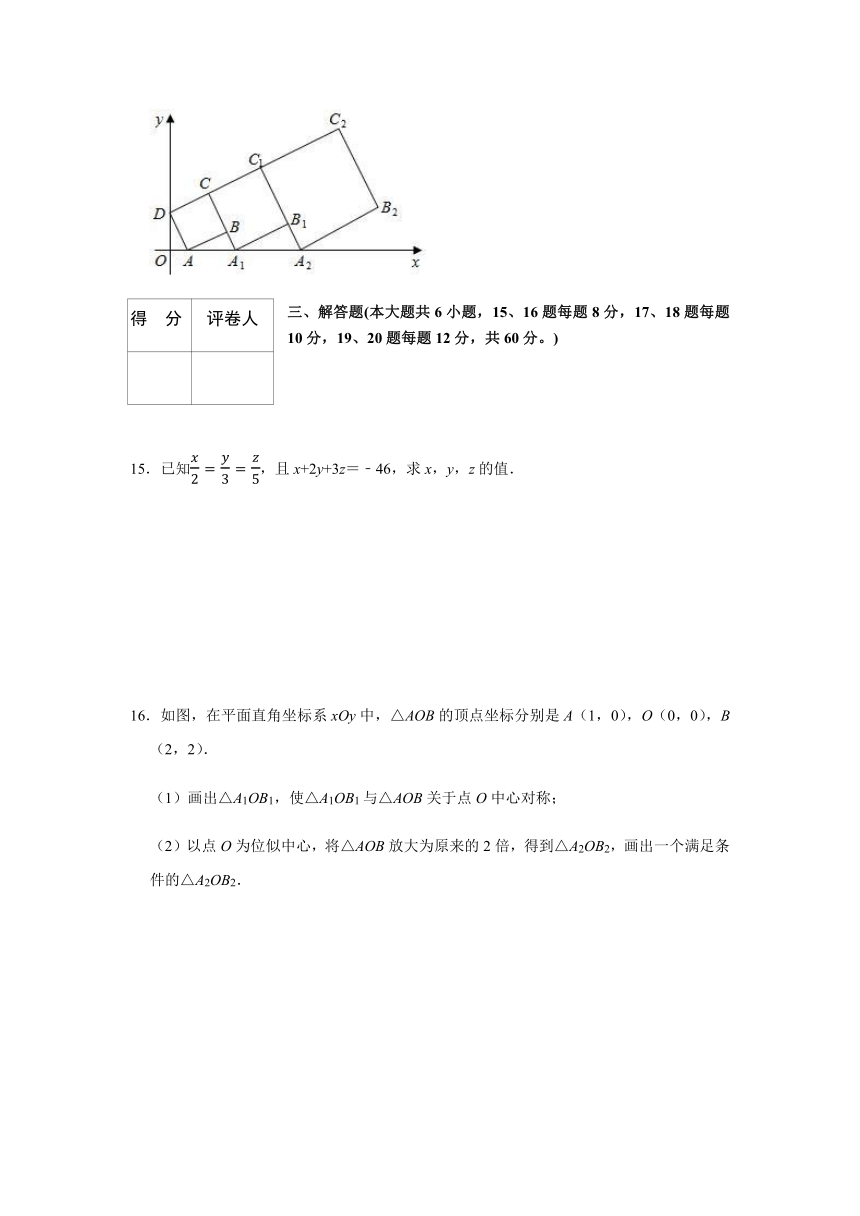
14.在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1…按这样的规律进行下去,第2020个正方形的面积为
.
得
分
评卷人
三、解答题(本大题共6小题,15、16题每题8分,17、18题每题10分,19、20题每题12分,共60分。)
已知,且x+2y+3z=﹣46,求x,y,z的值.
16.如图,在平面直角坐标系xOy中,△AOB的顶点坐标分别是A(1,0),O(0,0),B(2,2).
(1)画出△A1OB1,使△A1OB1与△AOB关于点O中心对称;
(2)以点O为位似中心,将△AOB放大为原来的2倍,得到△A2OB2,画出一个满足条件的△A2OB2.
17.如图,在等边△ABC中,P为BC上一点,D为AC上一点,且∠APD=60°,2BP=3CD,BP=1.
(1)求证△ABP∽△PCD;
(2)求△ABC的边长.
18.二次根式的除法,要化去分母中的根号,需将分子、分母同乘以一个恰当的二次根式.
例如:化简:.
解:将分子、分写同乘以得.
类比应用:(1)化简:
.
(2)化简:.
拓展延伸:宽与长的比是的矩形叫黄金矩形,如图①,已知黄金矩形ABCD的宽AB=1.
(1)黄金矩形ABCD的长BC=
;
(2)如图②,将图①中的黄金矩形裁剪掉一个以AB为边的正方形ABEF,得到新的矩形DCEF,猜想矩形DCEF是否为黄金矩形,并证明你的结论;
(3)在图②中,连结AE,则点D到线段AE的距离为
.
19.如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成矩形零件PQMN,使矩形PQMN的边QM在BC上,其余两个顶点P,N分别在AB,AC上.
(1)当矩形的边PN=PQ时,求此时矩形零件PQMN的面积;
(2)求这个矩形零件PQMN面积S的最大值.
20.如图,E是矩形ABCD的边BC上的一点,AC是其对角线,连接AE,过点E作EF⊥AE,EF交AC于点M,EF交DC于点F,过点B作BG⊥AC于点G,BG交AE于点H.
(1)求证:△ABE∽△ECF;
(2)求证:AH?CM=BH?EM;
(3)若E是BC的中点,,AB=6,求EM的长.
参考答案与试题解析
一.选择题(共10小题)
题序
1
2
3
4
5
6
7
8
9
10
答案
A
A
A
B
D
D
A
B
D
C
1.解:A、任意两个圆是相似图形,故此选项正确;
B、任意两个等腰三角形不是相似图形,故此选项错误;
C、任意两个菱形不是相似图形,故此选项错误;
D、任意两个矩形不是相似图形,故此选项错误;
故选:A.
2.解:∵AB=1,
设AD=x,则FD=x﹣1,FE=1,
∵四边形EFDC与矩形ABCD相似,
∴,,
解得x1,x2(不合题意舍去),
经检验x1是原方程的解.
故选:A.
3.解;∵DE∥BC,
∴,
∵,AD=6,
∴,
∴AB=8,
故选:A.
4.解:∵△ABC∽△A′B′C′,AD和A′D′是对应高,AD:A′D′=2,
∴△ABC与△A′B′C′的相似比为2:1,
∴△ABC与△A′B′C′的周长比为2:1,
故选:B.
5.解:∵∠1=∠2,
∴∠1+∠BAE=∠2+∠BAE,
∴∠DAE=∠BAC,
A、添加∠B=∠D可利用两角法:有两组角对应相等的两个三角形相似可得△ABC∽△ADE,故此选项不合题意;
B、添加∠C=∠E可利用两角法:有两组角对应相等的两个三角形相似可得△ABC∽△ADE,故此选项不合题意;
C、添加可利用两边对应成比例且夹角相等的两个三角形相似可得△ABC∽△ADE,故此选项不合题意;
D、添加不能证明△ABC∽△ADE,故此选项符合题意;
故选:D.
6.解:由作法得DE垂直平分BC,
∴DB=DC,
∴∠B=∠DCB,
∴∠ADC=∠B+∠DCB=2∠DCB,所以①正确;
∵DE垂直平分BC,
∴BE=CE,
而∠BAC=90°,
∴AE为斜边BC边上的中线,
∴AEBC,所以②正确;
∵AE=BE,
∴∠B=∠EAB,
∵∠B=∠DCB,
∴∠EAB=∠DCB,
∵∠FAD=∠FCE,∠AFD=∠CFE,
∴△ADF∽△CEF,
∴AF:CF=DF:EF,
∴AF?EF=DF?CF,所以③正确;
在Rt△ABC中,AC6,
∵DB=DC,
∴△ADC的周长=AD+CD+AC=AD+DB+AC=AB+AC=8+6=14,所以④正确.
故选:D.
7.解:如图,∵在Rt△ABC中,∠ACB=90°,CD⊥AB,
∴AC2=AD?AB,
又∵AC=3,AB=6,
∴32=6AD,则AD.
故选:A.
8.解:∵△OAB与△OCD是以点O为位似中心的位似图形,相似比为2,B(2,2),
∴点D的坐标为:(1,1).
故选:B.
9.解:∵∠DEF=∠BCD=90°,∠D=∠D,
∴△DEF∽△DCB,
∴BC:EF=DC:DE,
∵DE=30cm=0.3m,EF=15cm=1.5m,AC=1.5m,CD=7m,
∴,
∴BC=3.5米,
∴AB=AC+BC=1.5+3.5=5m,
故选:D.
10.解:如图,设EF=5cm,
∵裁出的是矩形纸条,
∴EF∥BC,
∴△AEF∽△ACB,
∴,即,
解得:AE=3.75(cm),
∴CE=AC﹣AE=30﹣3.75=26.25(cm),
∵裁得的纸条的长都不小于5cm,
∴CE≤26.25cm,
∵纸条宽度为1cm,
∴CE最大是26cm,
∴最多可以裁得的纸条的张数为26.
故选:C.
二.填空题(共4小题)
11.解:∵,
∴xy,
∴.
故答案为:.
12.解:∵BEAB,CFAC,
∴则,,
分别作EE1,FF1平行于BC且与AD交于E1、F1两点.
则EE1∥FF1,
∴△EE1P∽△FF1P,
,,,
又BD=CD,
∴,
∴,
故答案为:.
13.解:∵以原点O为位似中心,相似比为0.5,把△EFO缩小,得到△E'F'O,点E的坐标为(﹣4,2),
∴点E的对应点E'的坐标(﹣4,2)或(4,﹣2),即(﹣2,1)或(2,﹣1),
故答案为:(﹣2,1)或(2,﹣1).
14.解:∵正方形ABCD的点A的坐标为(1,0),点D的坐标为(0,2),
∴OA=1,OD=2,AD,,
延长CB交x轴于点A1,作正方形A1B1C1C,
∴△AA1B∽△DAO,
∴,
∵AD=AB,
∴A1B,
∴第1个正方形的面积为:S1=A1C2=()2=5?()2;
同理可得,A2C2=()2
第2个正方形的面积为:S2=5?()4
…
∴第2020个正方形的面积为:S2020=5?()4038.
故答案为:5?()4038.
三.解答题(共6小题)
15.解:设x=2k,y=3k,z=5k,(k≠0),
∵x+2y+3z=﹣46,
∴2k+6k+15k=﹣46,
解得:k=﹣2,
∴x=﹣4,y=﹣6,z=﹣10.
16.解:(1)如图,△A1OB1为所作;
(2)如图,△A2OB2为所作.
17.(1)证明:∵△ABC是等边三角形,
∴AB=BC=AC,∠B=∠C=60°,
∵∠BPA+∠APD+∠DPC=180°,且∠APD=60°,
∴∠BPA+∠DPC=120°,
∵∠DPC+∠C+∠PDC=180°,
∴∠DPC+∠PDC=120°,
∴∠BPA=∠PDC,
∴△ABP∽△PCD;
(2)解:∵2BP=3CD,且BP=1,
∴CD,
∵△ABP∽△PCD,
∴,
设AB=x,则PC=x﹣1,
∴,
∴x=3.
即AB=3.
∴△ABC的边长为3.
18.解:类比应用:(1)根据题意可得:
化简:2;
故答案为:2;
(2)根据题意可得:
原式1
=3﹣1
=2;
拓展延伸:
(1)∵宽与长的比是的矩形叫黄金矩形,
若黄金矩形ABCD的宽AB=1.
则黄金矩形ABCD的长BC为:
1:;
故答案为:;
(2)矩形DCEF是黄金矩形,理由如下:
由裁剪可知:
AB=AF=BE=EF=CD=1,
根据黄金矩形的性质可知:
AD=BC=1:;
∴FD=EC=AD﹣AF1,
∴1;
所以矩形DCEF是黄金矩形;
(3)如图,连接AE,DE,过点D作DG⊥AE于点G,
∵AB=EF=1,AD,
∴AE,
在△AED中,
S△AEDAD×EFAE×DG,
即AD×EF=AE×DG,
则1DG,
解得DG.
所以点D到线段AE的距离为.
故答案为:.
19.解:(1)设矩形零件PQMN的边PN=a,PQ=x,则AE=80﹣a.
∵PN∥BC,∴△APN∽△ABC.
∴.
因此,,
解得a=120x.
∴120x=x,
解得:x=48
所以长方形PQMN的面积S=xa=x(120x)x2+120x482+120×48=2304mm2
所以矩形零件PQMN的面积为2304mm2.
(2)由Sx2+120x,
当x40时,a=60.
S最大值=40×60=2400(mm2).
所以这个长方形零件PQMN面积S的最大值是2400mm2.
20.(1)证明:∵四边形ABCD是矩形,
∴∠ABE=∠ECF=90°.
∵AE⊥EF,∠AEB+∠FEC=90°.
∴∠AEB+∠BAE=90°,
∴∠BAE=∠CEF,
∴△ABE∽△ECF;
(2)证明:∵BG⊥AC,
∴∠ABG+∠BAG=90°,
∴∠ABH=∠ECM,
由(1)知,∠BAH=∠CEM,
∴△ABH∽△ECM;,
∴,
∴AH?CM=BH?EM;
(3)解:作MR⊥BC,垂足为R,
∵,AB=6,
∴BC=8,
∵E是BC的中点,
∴BE=EC=4,
∵△ABE∽△ECF,
∴,即
∴CF,
∵CD∥RM∥AB,
∴△ERM∽△ECF,△CRM∽△CBA,
∴,,即,,
∴RM,
∵,
∴,
∴,
∵△ABE∽△ECF,
∴,
∴,
∴EMRM.
《相似》
单
元
测
试
卷
题号
一
二
三
总分
得分
得
分
评卷人
一.单项选择题。(本大题共10小题,每小题4分,共40分。每小题只有一个正确答案,请将正确的答案的序号填入括号中。)
1.下列各组图形中,一定相似的是( )
A.任意两个圆
B.任意两个等腰三角形
C.任意两个菱形
D.任意两个矩形
2.如图,把矩形ABCD中的AB边向上翻折到AD边上,当点B与点F重合时,折痕与BC边交于点E,连接EF,若四边形EFDC与矩形ABCD恰好相似,若AB=1时,AD的长为( )
A.
B.
C.3
D.1
3.如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若,AD=6,则AB等于( )
A.8
B.6
C.4
D.2
4.已知△ABC∽△A′B′C′,AD和A′D′是对应高,且AD:A′D′=2,则它们的周长比是( )
A.1:2
B.2:1
C.1:4
D.4:1
5.如图,∠1=∠2,要使△ABC∽△ADE,只需要添加一个条件即可,这个条件不可能是( )
A.∠B=∠D
B.∠C=∠E
C.
D.
6.如图,在Rt△ABC中,按以下步骤作图:分别以B,C为圆心,以大于BC的长为半径作弧,弧线两两交于P、Q两点,作直线PQ,与边AB、BC分别交于D、E两点,连接CD、AE,AE、CD交于点F.在下列说法中:①∠ADC=2∠DCB;②AEBC;③AF?EF=DF?CF;④若AB=8,BC=10,则△ADC的周长为14.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
7.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,如果AC=3,AB=6,那么AD的值为( )
A.
B.
C.
D.3
8.如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为2,若A(4,0),B(2,2),则点D的坐标为( )
A.(1,2)
B.(1,1)
C.(,)
D.(2,1)
9.如图,小颖同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=30cm,EF=15cm,测得边DF离地面的高度AC=1.5m,CD=7m,则树高AB=( )m.
A.3.5
B.4
C.4.5
D.5
10.某公司在布置联欢会会场时,需要将直角三角形彩纸裁成长度不等的矩形纸条.如图所示:在Rt△ABC中,AC=30cm,BC=40cm.依此裁下宽度为1cm的纸条,若使裁得的纸条的长都不小于5cm,则能裁得的纸条的条数( )
A.24
B.25
C.26
D.27
得
分
评卷人
二、填空题(本大题共4小题,每小题5分,共20分。)
11.已知,那么
.
12.已知:△ABC中,D为BC的中点,E为AB上一点,且BEAB,F为AC上一点,且CFAC,EF交AD于P,则EP:PF=
.
13.在平面直角坐标系中,已知点E(﹣4,2),F(﹣2,﹣2).以原点O为位似中心,相似比为0.5,把△EFO缩小,得到△E'F'O,则点E的对应点E'的坐标是
.
14.在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1…按这样的规律进行下去,第2020个正方形的面积为
.
得
分
评卷人
三、解答题(本大题共6小题,15、16题每题8分,17、18题每题10分,19、20题每题12分,共60分。)
已知,且x+2y+3z=﹣46,求x,y,z的值.
16.如图,在平面直角坐标系xOy中,△AOB的顶点坐标分别是A(1,0),O(0,0),B(2,2).
(1)画出△A1OB1,使△A1OB1与△AOB关于点O中心对称;
(2)以点O为位似中心,将△AOB放大为原来的2倍,得到△A2OB2,画出一个满足条件的△A2OB2.
17.如图,在等边△ABC中,P为BC上一点,D为AC上一点,且∠APD=60°,2BP=3CD,BP=1.
(1)求证△ABP∽△PCD;
(2)求△ABC的边长.
18.二次根式的除法,要化去分母中的根号,需将分子、分母同乘以一个恰当的二次根式.
例如:化简:.
解:将分子、分写同乘以得.
类比应用:(1)化简:
.
(2)化简:.
拓展延伸:宽与长的比是的矩形叫黄金矩形,如图①,已知黄金矩形ABCD的宽AB=1.
(1)黄金矩形ABCD的长BC=
;
(2)如图②,将图①中的黄金矩形裁剪掉一个以AB为边的正方形ABEF,得到新的矩形DCEF,猜想矩形DCEF是否为黄金矩形,并证明你的结论;
(3)在图②中,连结AE,则点D到线段AE的距离为
.
19.如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成矩形零件PQMN,使矩形PQMN的边QM在BC上,其余两个顶点P,N分别在AB,AC上.
(1)当矩形的边PN=PQ时,求此时矩形零件PQMN的面积;
(2)求这个矩形零件PQMN面积S的最大值.
20.如图,E是矩形ABCD的边BC上的一点,AC是其对角线,连接AE,过点E作EF⊥AE,EF交AC于点M,EF交DC于点F,过点B作BG⊥AC于点G,BG交AE于点H.
(1)求证:△ABE∽△ECF;
(2)求证:AH?CM=BH?EM;
(3)若E是BC的中点,,AB=6,求EM的长.
参考答案与试题解析
一.选择题(共10小题)
题序
1
2
3
4
5
6
7
8
9
10
答案
A
A
A
B
D
D
A
B
D
C
1.解:A、任意两个圆是相似图形,故此选项正确;
B、任意两个等腰三角形不是相似图形,故此选项错误;
C、任意两个菱形不是相似图形,故此选项错误;
D、任意两个矩形不是相似图形,故此选项错误;
故选:A.
2.解:∵AB=1,
设AD=x,则FD=x﹣1,FE=1,
∵四边形EFDC与矩形ABCD相似,
∴,,
解得x1,x2(不合题意舍去),
经检验x1是原方程的解.
故选:A.
3.解;∵DE∥BC,
∴,
∵,AD=6,
∴,
∴AB=8,
故选:A.
4.解:∵△ABC∽△A′B′C′,AD和A′D′是对应高,AD:A′D′=2,
∴△ABC与△A′B′C′的相似比为2:1,
∴△ABC与△A′B′C′的周长比为2:1,
故选:B.
5.解:∵∠1=∠2,
∴∠1+∠BAE=∠2+∠BAE,
∴∠DAE=∠BAC,
A、添加∠B=∠D可利用两角法:有两组角对应相等的两个三角形相似可得△ABC∽△ADE,故此选项不合题意;
B、添加∠C=∠E可利用两角法:有两组角对应相等的两个三角形相似可得△ABC∽△ADE,故此选项不合题意;
C、添加可利用两边对应成比例且夹角相等的两个三角形相似可得△ABC∽△ADE,故此选项不合题意;
D、添加不能证明△ABC∽△ADE,故此选项符合题意;
故选:D.
6.解:由作法得DE垂直平分BC,
∴DB=DC,
∴∠B=∠DCB,
∴∠ADC=∠B+∠DCB=2∠DCB,所以①正确;
∵DE垂直平分BC,
∴BE=CE,
而∠BAC=90°,
∴AE为斜边BC边上的中线,
∴AEBC,所以②正确;
∵AE=BE,
∴∠B=∠EAB,
∵∠B=∠DCB,
∴∠EAB=∠DCB,
∵∠FAD=∠FCE,∠AFD=∠CFE,
∴△ADF∽△CEF,
∴AF:CF=DF:EF,
∴AF?EF=DF?CF,所以③正确;
在Rt△ABC中,AC6,
∵DB=DC,
∴△ADC的周长=AD+CD+AC=AD+DB+AC=AB+AC=8+6=14,所以④正确.
故选:D.
7.解:如图,∵在Rt△ABC中,∠ACB=90°,CD⊥AB,
∴AC2=AD?AB,
又∵AC=3,AB=6,
∴32=6AD,则AD.
故选:A.
8.解:∵△OAB与△OCD是以点O为位似中心的位似图形,相似比为2,B(2,2),
∴点D的坐标为:(1,1).
故选:B.
9.解:∵∠DEF=∠BCD=90°,∠D=∠D,
∴△DEF∽△DCB,
∴BC:EF=DC:DE,
∵DE=30cm=0.3m,EF=15cm=1.5m,AC=1.5m,CD=7m,
∴,
∴BC=3.5米,
∴AB=AC+BC=1.5+3.5=5m,
故选:D.
10.解:如图,设EF=5cm,
∵裁出的是矩形纸条,
∴EF∥BC,
∴△AEF∽△ACB,
∴,即,
解得:AE=3.75(cm),
∴CE=AC﹣AE=30﹣3.75=26.25(cm),
∵裁得的纸条的长都不小于5cm,
∴CE≤26.25cm,
∵纸条宽度为1cm,
∴CE最大是26cm,
∴最多可以裁得的纸条的张数为26.
故选:C.
二.填空题(共4小题)
11.解:∵,
∴xy,
∴.
故答案为:.
12.解:∵BEAB,CFAC,
∴则,,
分别作EE1,FF1平行于BC且与AD交于E1、F1两点.
则EE1∥FF1,
∴△EE1P∽△FF1P,
,,,
又BD=CD,
∴,
∴,
故答案为:.
13.解:∵以原点O为位似中心,相似比为0.5,把△EFO缩小,得到△E'F'O,点E的坐标为(﹣4,2),
∴点E的对应点E'的坐标(﹣4,2)或(4,﹣2),即(﹣2,1)或(2,﹣1),
故答案为:(﹣2,1)或(2,﹣1).
14.解:∵正方形ABCD的点A的坐标为(1,0),点D的坐标为(0,2),
∴OA=1,OD=2,AD,,
延长CB交x轴于点A1,作正方形A1B1C1C,
∴△AA1B∽△DAO,
∴,
∵AD=AB,
∴A1B,
∴第1个正方形的面积为:S1=A1C2=()2=5?()2;
同理可得,A2C2=()2
第2个正方形的面积为:S2=5?()4
…
∴第2020个正方形的面积为:S2020=5?()4038.
故答案为:5?()4038.
三.解答题(共6小题)
15.解:设x=2k,y=3k,z=5k,(k≠0),
∵x+2y+3z=﹣46,
∴2k+6k+15k=﹣46,
解得:k=﹣2,
∴x=﹣4,y=﹣6,z=﹣10.
16.解:(1)如图,△A1OB1为所作;
(2)如图,△A2OB2为所作.
17.(1)证明:∵△ABC是等边三角形,
∴AB=BC=AC,∠B=∠C=60°,
∵∠BPA+∠APD+∠DPC=180°,且∠APD=60°,
∴∠BPA+∠DPC=120°,
∵∠DPC+∠C+∠PDC=180°,
∴∠DPC+∠PDC=120°,
∴∠BPA=∠PDC,
∴△ABP∽△PCD;
(2)解:∵2BP=3CD,且BP=1,
∴CD,
∵△ABP∽△PCD,
∴,
设AB=x,则PC=x﹣1,
∴,
∴x=3.
即AB=3.
∴△ABC的边长为3.
18.解:类比应用:(1)根据题意可得:
化简:2;
故答案为:2;
(2)根据题意可得:
原式1
=3﹣1
=2;
拓展延伸:
(1)∵宽与长的比是的矩形叫黄金矩形,
若黄金矩形ABCD的宽AB=1.
则黄金矩形ABCD的长BC为:
1:;
故答案为:;
(2)矩形DCEF是黄金矩形,理由如下:
由裁剪可知:
AB=AF=BE=EF=CD=1,
根据黄金矩形的性质可知:
AD=BC=1:;
∴FD=EC=AD﹣AF1,
∴1;
所以矩形DCEF是黄金矩形;
(3)如图,连接AE,DE,过点D作DG⊥AE于点G,
∵AB=EF=1,AD,
∴AE,
在△AED中,
S△AEDAD×EFAE×DG,
即AD×EF=AE×DG,
则1DG,
解得DG.
所以点D到线段AE的距离为.
故答案为:.
19.解:(1)设矩形零件PQMN的边PN=a,PQ=x,则AE=80﹣a.
∵PN∥BC,∴△APN∽△ABC.
∴.
因此,,
解得a=120x.
∴120x=x,
解得:x=48
所以长方形PQMN的面积S=xa=x(120x)x2+120x482+120×48=2304mm2
所以矩形零件PQMN的面积为2304mm2.
(2)由Sx2+120x,
当x40时,a=60.
S最大值=40×60=2400(mm2).
所以这个长方形零件PQMN面积S的最大值是2400mm2.
20.(1)证明:∵四边形ABCD是矩形,
∴∠ABE=∠ECF=90°.
∵AE⊥EF,∠AEB+∠FEC=90°.
∴∠AEB+∠BAE=90°,
∴∠BAE=∠CEF,
∴△ABE∽△ECF;
(2)证明:∵BG⊥AC,
∴∠ABG+∠BAG=90°,
∴∠ABH=∠ECM,
由(1)知,∠BAH=∠CEM,
∴△ABH∽△ECM;,
∴,
∴AH?CM=BH?EM;
(3)解:作MR⊥BC,垂足为R,
∵,AB=6,
∴BC=8,
∵E是BC的中点,
∴BE=EC=4,
∵△ABE∽△ECF,
∴,即
∴CF,
∵CD∥RM∥AB,
∴△ERM∽△ECF,△CRM∽△CBA,
∴,,即,,
∴RM,
∵,
∴,
∴,
∵△ABE∽△ECF,
∴,
∴,
∴EMRM.
