第三章第六节带电粒子在匀强磁场中的运动(综合问题) 课件 23张PPT
文档属性
| 名称 | 第三章第六节带电粒子在匀强磁场中的运动(综合问题) 课件 23张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-02-22 18:59:32 | ||
图片预览






文档简介
学习目标
1.通过训练加深对洛伦兹力的理解
2.熟练掌握带电粒子在磁场中做匀速圆周运动的规律,重点会确定圆心,求解半径和时间。
3.6.4
带电粒子在匀强磁场中的运动(综合问题分析)
1
一、解决带电粒子在匀强磁场中的匀速圆周运动的方法和步骤
复习:
2
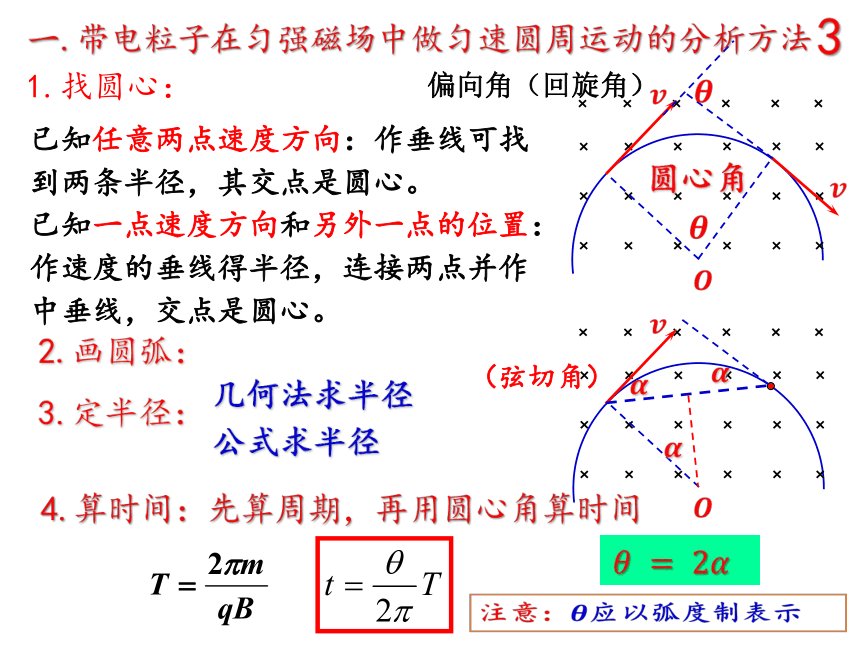
1.找圆心:
已知任意两点速度方向:作垂线可找到两条半径,其交点是圆心。
已知一点速度方向和另外一点的位置:作速度的垂线得半径,连接两点并作中垂线,交点是圆心。
????
?
????
?
????
?
????
?
????
?
3.定半径:
几何法求半径
公式求半径
4.算时间:先算周期,再用圆心角算时间
????
?
????
?
????
?
????
?
????
?
?????=?2????
?
注意:????应以弧度制表示
?
2.画圆弧:
圆心角
偏向角(回旋角)
(弦切角)
一.带电粒子在匀强磁场中做匀速圆周运动的分析方法
3
二、带电粒子在电场,磁场,重力场等多个场共同作用下该如何运动?
4
1.对带电粒子进行受力分析,特别注意电场力和磁场力的特点。
2.分析带电粒子在复合场中的运动图景
3.抽象出运动模型
4.运用物理规律对粒子运动进行数学描述,建立相关的几何关系方程
5.建立方程求解
特别受数学知识限制
5
三、带电粒子在有界磁场中的圆周运动的临界问题如何分析
6
B
v
O
边界圆
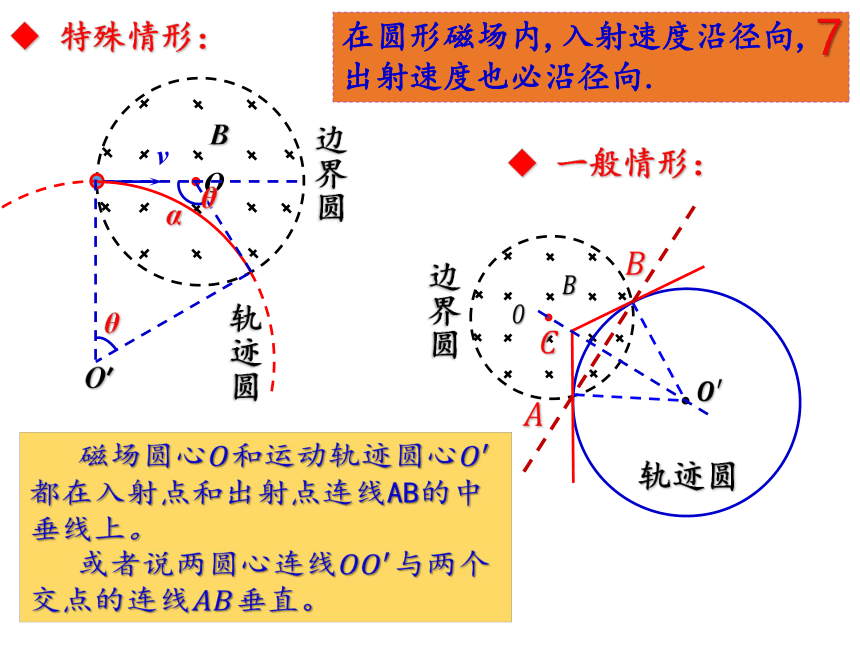
特殊情形:
轨迹圆
O′
α
θ
θ
在圆形磁场内,入射速度沿径向,出射速度也必沿径向.
????
?
????
?
边界圆
轨迹圆
????
?
????
?
????
?
????′
?
一般情形:
磁场圆心????和运动轨迹圆心????′都在入射点和出射点连线AB的中垂线上。
或者说两圆心连线????????′与两个交点的连线????????垂直。
?
7
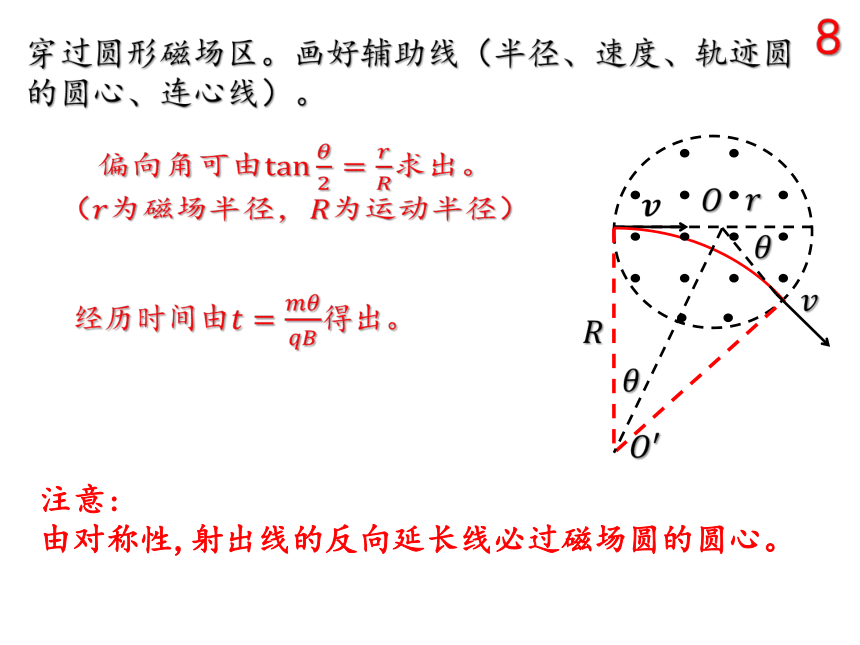
穿过圆形磁场区。画好辅助线(半径、速度、轨迹圆的圆心、连心线)。
偏向角可由tan????2=????????求出。
(????为磁场半径,????为运动半径)
?
经历时间由????=????????????????得出。
?
注意:
由对称性,射出线的反向延长线必过磁场圆的圆心。
????
?
????
?
????
?
????′
?
????
?
????
?
????
?
????
?
8
2.带电粒子在磁场中运动多解问题的解题思路:
①画出运动轨迹;确定圆心。
②利用几何关系计算半径。
③由????????????=????????2????和圆周运动等知识求解。
?
⑴明确多解原因。
⑵分别设每种多解原因成立,进行分析求解。
⑶求解过程同带电粒子在磁场中圆周运动的分析方法,即:
9
1.如图所示,相互垂直的匀强电场和匀强磁场的大小分别为????和????,一个质量为????、电量为+????的油滴,从????点以水平速度????0飞入,经过一段时间后运动到????点,试计算:
(1)油滴刚进入叠加场????点时的加速度;
(2)若到达????点时,偏离入射方向的距离为????,则其速度是多大?
?
1.叠加场
方向:竖直向上
????????0??????????????????????????
?
????02?2?????????2????????????????
?
10
1.如图所示,在匀强电场和匀强磁场共存的区域内,电场的电场强度为????,方向竖直向下,磁场的磁感应强度为????,方向垂直于纸面向里,一质量为????的带电粒子,在场区内的一竖直平面内做匀速圆周运动,则可判断该带电质点( )
A.带有电荷量为????????????的负电荷
B.沿圆周逆时针运动
C.运动的角速度为????????????
D.运动的速率为????????
?
????????
?
11
1.本题从何处入手能快速解题?
甭管是什么电性,做的运动为匀速圆周运动,那么在两侧位置所受合力必指向圆心。即合力方向为水平向。故:重力=电场力
由此可判断电性为:负电,通过左手定则可判断,顺时针方向运动,且重力????????=电场力????????,得电量????=????????????
?
2.如何计算角速度与线速度
由向心力公式:????????????=????????2????可得:????2=????????????????????又????=????????????????联立得:????2=????2????2????2即:????=????????????其中????=????????????,联立得????=????????????
?
或者利用公式:????????????=????????????可快速计算
?
2.如图所示,在????轴上方有垂直于????????????平面向里的匀强磁场,磁感应强度为????;在????轴下方有沿????轴负方向的匀强电场,场强为????.一质量为????、电荷量为?????的粒子从坐标原点沿着????轴正方向射出.射出之后,第3次到达????轴时,它与点????的距离为????,求此粒子射出时的速度????和运动的总路程????.(重力不计)
?
2.组合场
12
在磁场中匀速圆周运动,则????????????=????????2????得????=????????????????
第3次到达????轴时,距离????点????距离,即:
????=4????
联立:????=????????????4????
?
运动距离为:两个半圆周长+电场中往复运动距离
两个半圆周长:????1=2????????=????????2
电场运动距离:????????????=12????????2→????=????????22????????→????2=2????=????????2????216????????
?
3.在如图所示的平面直角坐标系????????????中,有一个圆形区域的匀强磁场(图中未画出),磁场方向垂直于????????????平面,????点为该圆形区域边界上的一点.现有一质量为????,带电量为+????的带电粒子(不计重力)从????点为以初速度????0沿????轴方向进入磁场,已知粒子经过????轴上????点时速度方向与+????方向夹角为????=30°,????????=????.求:
(1)磁感应强度的大小和方向.
(2)该圆形磁场区域的最小面积.
?
二.磁场面积最值问题
13
????????
?
????
?
????
?
????
?
????
?
????
?
????
?
1.根据左手定则判断磁场方向,画出运动轨迹,然后求解出轨道半径,最后根据洛伦兹力提供向心力列式求解。
2.先求出连接粒子在磁场区入射点和初射点的弦长,要是圆形匀强磁场区域面积最小,其半径刚好为弦长的一半,求出半径即可求得面积
14
3.在如图所示的平面直角坐标系????????????中,有一个圆形区域的匀强磁场(图中未画出),磁场方向垂直于????????????平面,????点为该圆形区域边界上的一点.现有一质量为????,带电量为+????的带电粒子(不计重力)从????点为以初速度????0沿????轴方向进入磁场,已知粒子经过????轴上????点时速度方向与+????方向夹角为????=30°,????????=????.求:
(1)磁感应强度的大小和方向.
?
????????
?
????
?
????
?
????
?
????
?
????
?
????
?
匀强磁场第一种情况(已知任意两点速度方向),作图。
几何关系:(?????????)sin30°=????
?
????=13????
?
半径确定,其余简单:
????????0????=????????02????
?
????=????????0????????
?
????=3????????0????????
?
→
?
→
?
15
3.在如图所示的平面直角坐标系????????????中,有一个圆形区域的匀强磁场(图中未画出),磁场方向垂直于????????????平面,????点为该圆形区域边界上的一点.现有一质量为????,带电量为+????的带电粒子(不计重力)从????点为以初速度????0沿????轴方向进入磁场,已知粒子经过????轴上????点时速度方向与+????方向夹角为????=30°,????????=????.求:
(2)该圆形磁场区域的最小面积.
?
????????
?
????
?
????
?
????
?
????
?
????
?
????
?
明确磁场最小区域的边界在何处是关键
????′
?
????
?
当????????做直径时,即为磁场最小面积,
????????=3????=33????
?
????=????????????????????
?
2.一质量为????、电荷量为+????的粒子以速度????,从????点沿????轴正方向射入磁感应强度为????的圆形匀强磁场区域,磁场方向垂直纸面向外,粒子飞出磁场区域后,从????处穿过????轴,速度方向与????轴正方向的夹角为30°,同时进入场强为????、方向沿与????轴负方向成60°角斜向下的匀强电场中,通过了????点正下方的????点,如图所示,粒子的重力不计,试求:
(1)圆形匀强磁场区域的最小面积;
(2)????点到????点的距离。
?
16
1.粒子在匀强磁场中做匀速圆周运动,由牛顿第二定律求粒子的轨道半径,然后由数学知识求出磁场的最小面积。
2.粒子在匀强电场中类平抛运动,由类平抛运动知识可以求出????????间的距离。
?
2.一质量为????、电荷量为+????的粒子以速度????,从????点沿????轴正方向射入磁感应强度为????的圆形匀强磁场区域,磁场方向垂直纸面向外,粒子飞出磁场区域后,从????处穿过????轴,速度方向与????轴正方向的夹角为30°,同时进入场强为????、方向沿与????轴负方向成60°角斜向下的匀强电场中,通过了????点正下方的????点,如图所示,粒子的重力不计,试求:
(1)圆形匀强磁场区域的最小面积;
?
17
磁场区域的最小半径:
????=????cos30°
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
当以????????为直径时,有最小磁场面积。
?
磁场最小面积:
????=????????2=3????????2????24????2????2
?
18
2.一质量为????、电荷量为+????的粒子以速度????,从????点沿????轴正方向射入磁感应强度为????的圆形匀强磁场区域,磁场方向垂直纸面向外,粒子飞出磁场区域后,从????处穿过????轴,速度方向与????轴正方向的夹角为30°,同时进入场强为????、方向沿与????轴负方向成60°角斜向下的匀强电场中,通过了????点正下方的????点,如图所示,粒子的重力不计,试求:
(2)????点到????点的距离。
?
粒子在????轴下方作类平抛运动。
垂直电场方向做匀速运动,沿电场方向做匀速运动,位移与初速度方向夹角为60°
?
tan60°=????????=12??????????????????2????????
?
????=23????????????????
?
????????间距离:????????cos60°=43????????2????????
?
如图所示,在半径为????的圆形区域内,有匀强磁场,磁感应强度为????,方向垂直于圆平面(未画出)。一群比荷为????/????的负离子体以相同速率????0(较大)由????点在纸平面内向不同方向射入磁场中发生偏转后,又飞出磁场,则下列说法正确的是(不计重力)
A.离子飞出磁场时的动能一定相等
B.离子在磁场中运动半径一定相等
C.由????点飞出的离子在磁场中运动的时间最长
D.沿????????方向射入的离子飞出时偏转角最大
?
三.动态圆问题
????????
?
19
有图可知:在所有过????点的半径恒定的圆中,????????弦长最长,所对的圆心角最大。故粒子运动时间最长。
?
20
课堂小结:
1.基本公式需熟练掌握:
3.注意题设中的隐含条件和临界条件
2.画轨迹找几何关系列相应方程
1)确定圆心;2)求半径;3)求时间
21
22
1.如图所示,一足够长的区域????????????????内充满磁感应强度为????、方向垂直纸面向里的匀强磁场,其中????????平行于????????,????????与上、下边界垂直.现从????????边的中点????处,垂直磁场射入一速度方向与????????边夹角为30°、大小为????0的带正电粒子,已知粒子质量为????,电荷量为????,????????边长为????,重力影响不计.
(1)试求粒子能从????????边上射出磁场的????0的大小范围;
(2)问粒子在磁场中运动的最长时间是多少?
?
(1)????=???????????? (方向竖直向上)
(2)????0=????????????2????tan????
(3)?=????2????2????28????2????
?
23
2.如图所示,直角坐标系????????????位于竖直平面内,在水平的????轴下方存在匀强磁场和匀强电场,磁场的磁感应强度为????,方向垂直 ????????????平面向里,电场线平行于????轴.一质量为????、电荷量为????的带正电的小球,从????轴上的????点水平向右抛出,经????轴上的????点进入电场和磁场,恰能做匀速圆周运动,从????轴上的????点第一次离开电场和磁场,????????之间的距离为????,小球过????点时的速度方向与????轴的方向夹角为????.不计空气阻力,重力加速度为????,求:
(1)电场强度????的大小和方向;
(2)小球从????点水平抛出时初速度????0的大小;
(3)????点到????轴的高度?.
1.通过训练加深对洛伦兹力的理解
2.熟练掌握带电粒子在磁场中做匀速圆周运动的规律,重点会确定圆心,求解半径和时间。
3.6.4
带电粒子在匀强磁场中的运动(综合问题分析)
1
一、解决带电粒子在匀强磁场中的匀速圆周运动的方法和步骤
复习:
2
1.找圆心:
已知任意两点速度方向:作垂线可找到两条半径,其交点是圆心。
已知一点速度方向和另外一点的位置:作速度的垂线得半径,连接两点并作中垂线,交点是圆心。
????
?
????
?
????
?
????
?
????
?
3.定半径:
几何法求半径
公式求半径
4.算时间:先算周期,再用圆心角算时间
????
?
????
?
????
?
????
?
????
?
?????=?2????
?
注意:????应以弧度制表示
?
2.画圆弧:
圆心角
偏向角(回旋角)
(弦切角)
一.带电粒子在匀强磁场中做匀速圆周运动的分析方法
3
二、带电粒子在电场,磁场,重力场等多个场共同作用下该如何运动?
4
1.对带电粒子进行受力分析,特别注意电场力和磁场力的特点。
2.分析带电粒子在复合场中的运动图景
3.抽象出运动模型
4.运用物理规律对粒子运动进行数学描述,建立相关的几何关系方程
5.建立方程求解
特别受数学知识限制
5
三、带电粒子在有界磁场中的圆周运动的临界问题如何分析
6
B
v
O
边界圆
特殊情形:
轨迹圆
O′
α
θ
θ
在圆形磁场内,入射速度沿径向,出射速度也必沿径向.
????
?
????
?
边界圆
轨迹圆
????
?
????
?
????
?
????′
?
一般情形:
磁场圆心????和运动轨迹圆心????′都在入射点和出射点连线AB的中垂线上。
或者说两圆心连线????????′与两个交点的连线????????垂直。
?
7
穿过圆形磁场区。画好辅助线(半径、速度、轨迹圆的圆心、连心线)。
偏向角可由tan????2=????????求出。
(????为磁场半径,????为运动半径)
?
经历时间由????=????????????????得出。
?
注意:
由对称性,射出线的反向延长线必过磁场圆的圆心。
????
?
????
?
????
?
????′
?
????
?
????
?
????
?
????
?
8
2.带电粒子在磁场中运动多解问题的解题思路:
①画出运动轨迹;确定圆心。
②利用几何关系计算半径。
③由????????????=????????2????和圆周运动等知识求解。
?
⑴明确多解原因。
⑵分别设每种多解原因成立,进行分析求解。
⑶求解过程同带电粒子在磁场中圆周运动的分析方法,即:
9
1.如图所示,相互垂直的匀强电场和匀强磁场的大小分别为????和????,一个质量为????、电量为+????的油滴,从????点以水平速度????0飞入,经过一段时间后运动到????点,试计算:
(1)油滴刚进入叠加场????点时的加速度;
(2)若到达????点时,偏离入射方向的距离为????,则其速度是多大?
?
1.叠加场
方向:竖直向上
????????0??????????????????????????
?
????02?2?????????2????????????????
?
10
1.如图所示,在匀强电场和匀强磁场共存的区域内,电场的电场强度为????,方向竖直向下,磁场的磁感应强度为????,方向垂直于纸面向里,一质量为????的带电粒子,在场区内的一竖直平面内做匀速圆周运动,则可判断该带电质点( )
A.带有电荷量为????????????的负电荷
B.沿圆周逆时针运动
C.运动的角速度为????????????
D.运动的速率为????????
?
????????
?
11
1.本题从何处入手能快速解题?
甭管是什么电性,做的运动为匀速圆周运动,那么在两侧位置所受合力必指向圆心。即合力方向为水平向。故:重力=电场力
由此可判断电性为:负电,通过左手定则可判断,顺时针方向运动,且重力????????=电场力????????,得电量????=????????????
?
2.如何计算角速度与线速度
由向心力公式:????????????=????????2????可得:????2=????????????????????又????=????????????????联立得:????2=????2????2????2即:????=????????????其中????=????????????,联立得????=????????????
?
或者利用公式:????????????=????????????可快速计算
?
2.如图所示,在????轴上方有垂直于????????????平面向里的匀强磁场,磁感应强度为????;在????轴下方有沿????轴负方向的匀强电场,场强为????.一质量为????、电荷量为?????的粒子从坐标原点沿着????轴正方向射出.射出之后,第3次到达????轴时,它与点????的距离为????,求此粒子射出时的速度????和运动的总路程????.(重力不计)
?
2.组合场
12
在磁场中匀速圆周运动,则????????????=????????2????得????=????????????????
第3次到达????轴时,距离????点????距离,即:
????=4????
联立:????=????????????4????
?
运动距离为:两个半圆周长+电场中往复运动距离
两个半圆周长:????1=2????????=????????2
电场运动距离:????????????=12????????2→????=????????22????????→????2=2????=????????2????216????????
?
3.在如图所示的平面直角坐标系????????????中,有一个圆形区域的匀强磁场(图中未画出),磁场方向垂直于????????????平面,????点为该圆形区域边界上的一点.现有一质量为????,带电量为+????的带电粒子(不计重力)从????点为以初速度????0沿????轴方向进入磁场,已知粒子经过????轴上????点时速度方向与+????方向夹角为????=30°,????????=????.求:
(1)磁感应强度的大小和方向.
(2)该圆形磁场区域的最小面积.
?
二.磁场面积最值问题
13
????????
?
????
?
????
?
????
?
????
?
????
?
????
?
1.根据左手定则判断磁场方向,画出运动轨迹,然后求解出轨道半径,最后根据洛伦兹力提供向心力列式求解。
2.先求出连接粒子在磁场区入射点和初射点的弦长,要是圆形匀强磁场区域面积最小,其半径刚好为弦长的一半,求出半径即可求得面积
14
3.在如图所示的平面直角坐标系????????????中,有一个圆形区域的匀强磁场(图中未画出),磁场方向垂直于????????????平面,????点为该圆形区域边界上的一点.现有一质量为????,带电量为+????的带电粒子(不计重力)从????点为以初速度????0沿????轴方向进入磁场,已知粒子经过????轴上????点时速度方向与+????方向夹角为????=30°,????????=????.求:
(1)磁感应强度的大小和方向.
?
????????
?
????
?
????
?
????
?
????
?
????
?
????
?
匀强磁场第一种情况(已知任意两点速度方向),作图。
几何关系:(?????????)sin30°=????
?
????=13????
?
半径确定,其余简单:
????????0????=????????02????
?
????=????????0????????
?
????=3????????0????????
?
→
?
→
?
15
3.在如图所示的平面直角坐标系????????????中,有一个圆形区域的匀强磁场(图中未画出),磁场方向垂直于????????????平面,????点为该圆形区域边界上的一点.现有一质量为????,带电量为+????的带电粒子(不计重力)从????点为以初速度????0沿????轴方向进入磁场,已知粒子经过????轴上????点时速度方向与+????方向夹角为????=30°,????????=????.求:
(2)该圆形磁场区域的最小面积.
?
????????
?
????
?
????
?
????
?
????
?
????
?
????
?
明确磁场最小区域的边界在何处是关键
????′
?
????
?
当????????做直径时,即为磁场最小面积,
????????=3????=33????
?
????=????????????????????
?
2.一质量为????、电荷量为+????的粒子以速度????,从????点沿????轴正方向射入磁感应强度为????的圆形匀强磁场区域,磁场方向垂直纸面向外,粒子飞出磁场区域后,从????处穿过????轴,速度方向与????轴正方向的夹角为30°,同时进入场强为????、方向沿与????轴负方向成60°角斜向下的匀强电场中,通过了????点正下方的????点,如图所示,粒子的重力不计,试求:
(1)圆形匀强磁场区域的最小面积;
(2)????点到????点的距离。
?
16
1.粒子在匀强磁场中做匀速圆周运动,由牛顿第二定律求粒子的轨道半径,然后由数学知识求出磁场的最小面积。
2.粒子在匀强电场中类平抛运动,由类平抛运动知识可以求出????????间的距离。
?
2.一质量为????、电荷量为+????的粒子以速度????,从????点沿????轴正方向射入磁感应强度为????的圆形匀强磁场区域,磁场方向垂直纸面向外,粒子飞出磁场区域后,从????处穿过????轴,速度方向与????轴正方向的夹角为30°,同时进入场强为????、方向沿与????轴负方向成60°角斜向下的匀强电场中,通过了????点正下方的????点,如图所示,粒子的重力不计,试求:
(1)圆形匀强磁场区域的最小面积;
?
17
磁场区域的最小半径:
????=????cos30°
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
当以????????为直径时,有最小磁场面积。
?
磁场最小面积:
????=????????2=3????????2????24????2????2
?
18
2.一质量为????、电荷量为+????的粒子以速度????,从????点沿????轴正方向射入磁感应强度为????的圆形匀强磁场区域,磁场方向垂直纸面向外,粒子飞出磁场区域后,从????处穿过????轴,速度方向与????轴正方向的夹角为30°,同时进入场强为????、方向沿与????轴负方向成60°角斜向下的匀强电场中,通过了????点正下方的????点,如图所示,粒子的重力不计,试求:
(2)????点到????点的距离。
?
粒子在????轴下方作类平抛运动。
垂直电场方向做匀速运动,沿电场方向做匀速运动,位移与初速度方向夹角为60°
?
tan60°=????????=12??????????????????2????????
?
????=23????????????????
?
????????间距离:????????cos60°=43????????2????????
?
如图所示,在半径为????的圆形区域内,有匀强磁场,磁感应强度为????,方向垂直于圆平面(未画出)。一群比荷为????/????的负离子体以相同速率????0(较大)由????点在纸平面内向不同方向射入磁场中发生偏转后,又飞出磁场,则下列说法正确的是(不计重力)
A.离子飞出磁场时的动能一定相等
B.离子在磁场中运动半径一定相等
C.由????点飞出的离子在磁场中运动的时间最长
D.沿????????方向射入的离子飞出时偏转角最大
?
三.动态圆问题
????????
?
19
有图可知:在所有过????点的半径恒定的圆中,????????弦长最长,所对的圆心角最大。故粒子运动时间最长。
?
20
课堂小结:
1.基本公式需熟练掌握:
3.注意题设中的隐含条件和临界条件
2.画轨迹找几何关系列相应方程
1)确定圆心;2)求半径;3)求时间
21
22
1.如图所示,一足够长的区域????????????????内充满磁感应强度为????、方向垂直纸面向里的匀强磁场,其中????????平行于????????,????????与上、下边界垂直.现从????????边的中点????处,垂直磁场射入一速度方向与????????边夹角为30°、大小为????0的带正电粒子,已知粒子质量为????,电荷量为????,????????边长为????,重力影响不计.
(1)试求粒子能从????????边上射出磁场的????0的大小范围;
(2)问粒子在磁场中运动的最长时间是多少?
?
(1)????=???????????? (方向竖直向上)
(2)????0=????????????2????tan????
(3)?=????2????2????28????2????
?
23
2.如图所示,直角坐标系????????????位于竖直平面内,在水平的????轴下方存在匀强磁场和匀强电场,磁场的磁感应强度为????,方向垂直 ????????????平面向里,电场线平行于????轴.一质量为????、电荷量为????的带正电的小球,从????轴上的????点水平向右抛出,经????轴上的????点进入电场和磁场,恰能做匀速圆周运动,从????轴上的????点第一次离开电场和磁场,????????之间的距离为????,小球过????点时的速度方向与????轴的方向夹角为????.不计空气阻力,重力加速度为????,求:
(1)电场强度????的大小和方向;
(2)小球从????点水平抛出时初速度????0的大小;
(3)????点到????轴的高度?.
