第五章 曲线运动章末复习课件 20张PPT
文档属性
| 名称 | 第五章 曲线运动章末复习课件 20张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-02-22 19:12:01 | ||
图片预览





文档简介
第五章
抛体运动章末复习
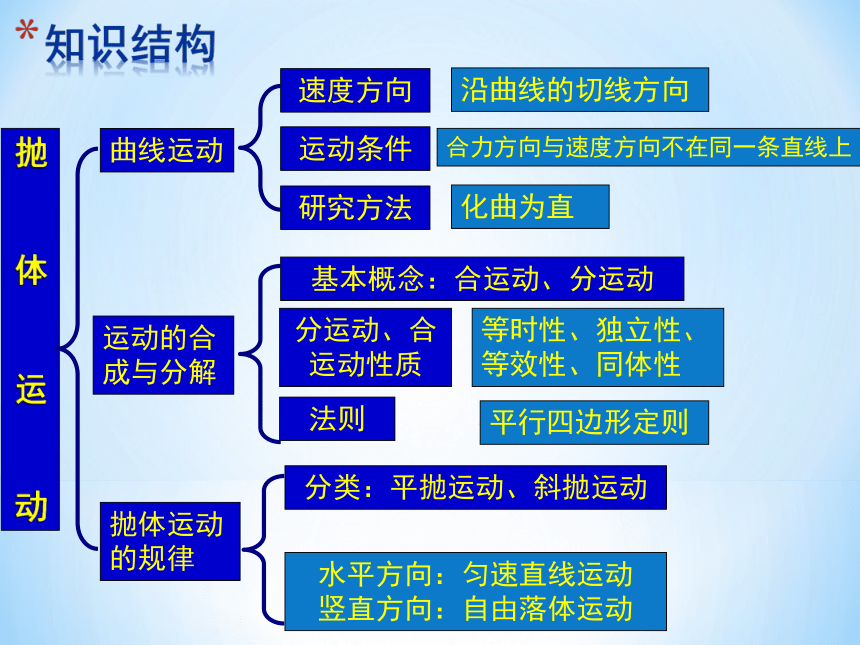
抛 体 运 动
曲线运动
运动的合
成与分解
抛体运动的规律
速度方向
法则
沿曲线的切线方向
合力方向与速度方向不在同一条直线上
等时性、独立性、
等效性、同体性
化曲为直
平行四边形定则
知识结构
运动条件
研究方法
基本概念:合运动、分运动
分运动、合运动性质
分类:平抛运动、斜抛运动
水平方向:匀速直线运动
竖直方向:自由落体运动
2. 运动性质:
轨迹是曲线;运动方向时刻在改变是 ;一定具有加速度, 。
3、运动的条件:运动物体所受合外力方向跟它的速度方向 。
1.速度方向:做曲线运动的物体在某点速度方向是曲线在该点的 。
变速运动
合外力不为零
切线方向
不在同一直线上
4、轨迹特点:物体曲线运动的轨迹应在合力F与速度v方向之间,并且合力F指向 。
轨迹的内侧
一:曲线运动
1、速度变化的运动必是曲线运动吗?
2、加速度变化的运动必是曲线运动吗?
3、曲线运动一定是变速运动?
4、变速运动一定是曲线运动?
5、曲线运动的速度一定变?
6、做曲线运动的物体所受合力一定不为零?
7、物体在恒力下不可能做曲线运动?
8、物体在变力作用下一定做曲线运动?
9、加速度恒定的运动不可能是曲线运动?
错
错
错
错
错
错
对
对
对
练习1
1、基本概念:合运动:物体 ;
3、特点:
4、法则:
运动的合成具有惟一性,而运动的分解不惟一,通常按运动所产生的实际效果分解。
分运动:物体同时参与合成的运动的运动。
等时性、独立性、等效性、同体性
平行四边形定则(或三角形定则)
实际的运动
2、实质:运动的合成与分解是指 的合成与分解。
a、v、x
二:运动的合成与分解
1)是直线运动还是曲线运动?(判断轨迹)
2)是匀变速运动还是变加速运动?(判断运动性质)
判断:不在一直线上的两个匀速直线运动的合运动?一个匀速直线运动与一个匀加速直线运动的合运动?两个匀变速直线运动的合运动?
回忆:如何判断两个直线运动的合运动的运动轨迹和运动性质?
合力F合的方向或加速度a的方向与合速度v合的方向是否同一直线
合力或加速度是否恒定
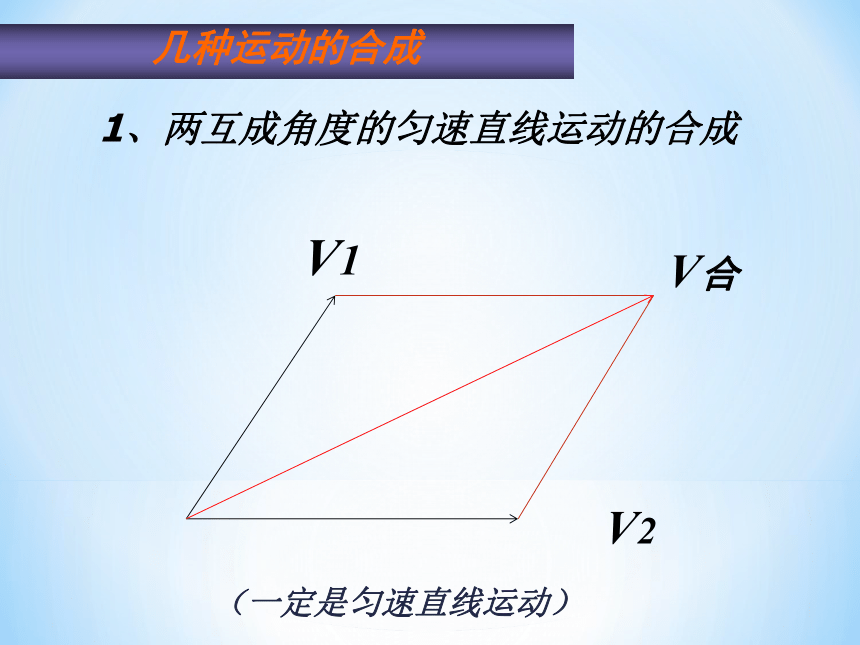
几种运动的合成
1、两互成角度的匀速直线运动的合成
(一定是匀速直线运动)
V2
V1
V合
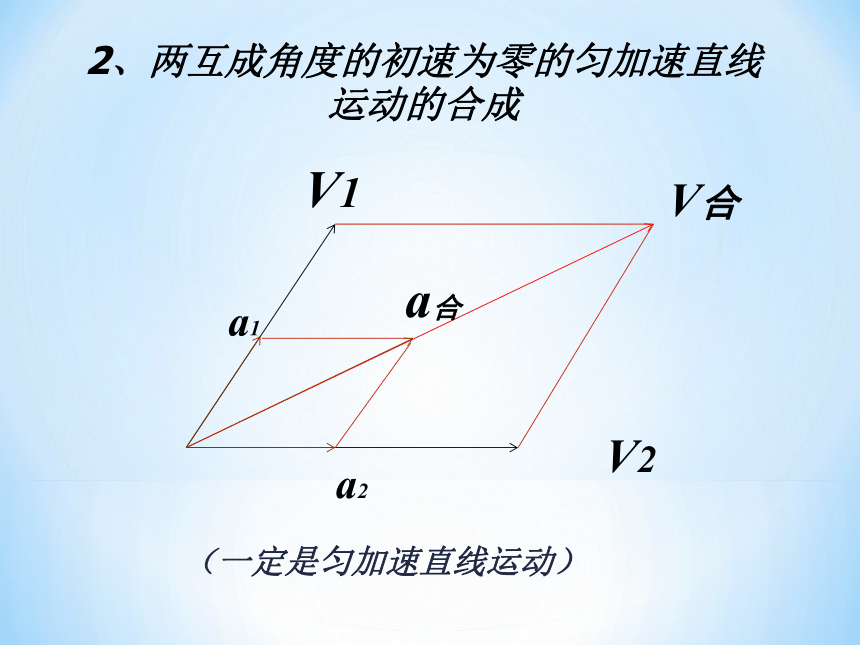
2、两互成角度的初速为零的匀加速直线运动的合成
(一定是匀加速直线运动)
V2
V合
V1
a合
a2
a1
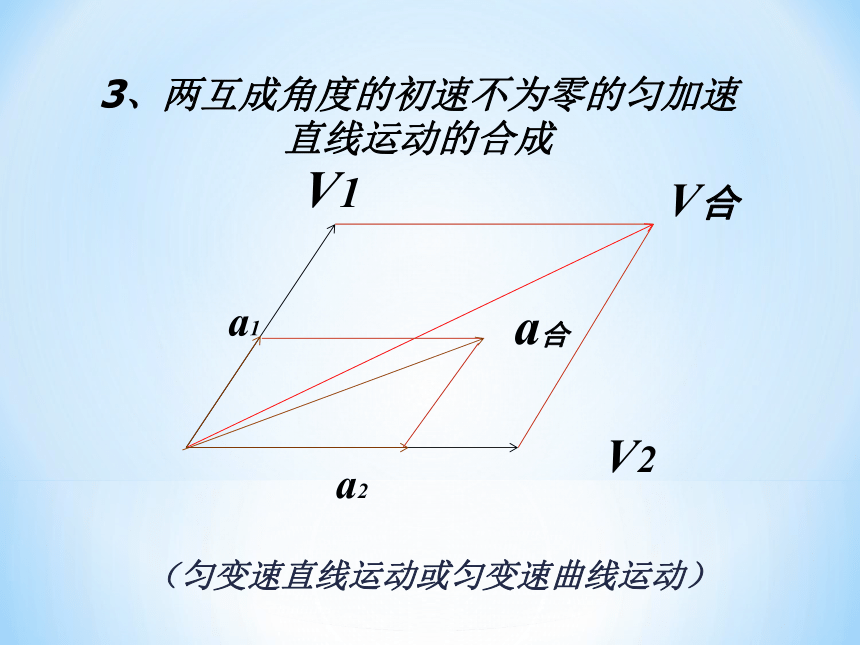
3、两互成角度的初速不为零的匀加速直线运动的合成
(匀变速直线运动或匀变速曲线运动)
V2
V合
V1
a合
a2
a1
4、一个匀速直线运动和一个匀加速直线运动的合成
(匀变速直线运动或匀变速曲线运动)
V2
V合
a
V1
1.曲线运动一定是变速运动。
2.合运动的加速度为分运动的加速度矢量和。
3.如果做曲线运动的物体运动速度大小没有发生变化,则物体加速度为零。
4.物体在变力或恒力作用下都可能作直线运动。
5.物体所受的合外力方向与速度的方向不在同一条直线上,物体就作曲线运动。
6.静止物体在恒力作用下一定做匀加速直线运动。
7.物体受到多力作用而在做匀速运动,当撤去一个力时物体运动做匀变速运动。
8.平抛运动是匀变速曲线运动。
9.如果平抛物体运动时间足够长,则其速度方向将变为竖直向下。
10.向心加速度的物理意义是描述做圆周运动的质点向心力变化的快慢。
概念判断:
方法1.按运动的实际效果分解
方法2.正交分解
1)分解的原则
2)运动分解的典型问题
a.小船过河问题
b.关联速度问题
运动的分解
小船过河问题:
船速为v1 水速为v2
当v1 >v2
1)时间最短
2)位移最小
d
d
d
过河时间:
θ
v1
v2
v
?
沿绳方向的伸长或收缩运动
垂直于绳方向的旋转运动
则V与V1的关系为 ?
关联速度问题
“关联速度”问题解题关键:
1.沿绳(或杆)速度大小相同
2.物体实际的运动是合运动
3、处理方法:
2、性质:
化曲为直:
分解为水平方向的匀速直线运动和竖直方向的自由落体运动。
匀变速曲线运动
1、条件:
①具有 ;
② 。
水平的初速度
只受重力
三:抛体运动的规律
平抛运动
4、平抛运动速度和位移
VO
mg
o
x
y
vx
vy
v
t
①平抛物体在 t 时刻的瞬时速度:
水平方向:vx=vo
竖直方向:vy=gt
速度方向:(与水平方向夹角)
tan α =vy/vx=gt/vo
α
VO
mg
o
x
y
y
x
s
t
②平抛物体在 t 时刻的位移:
水平方向: x=vot
竖直方向:y=1/2gt2
位移方向:(与水平方向夹角)
tan?=y/x = gt/2vo
β
tan α =2 tan?
已知tan α =vy/vx=gt/vo
平抛运动任意时刻速度的反向延长线一定经过此时水平位移的中点
做平抛运动的物体垂直落在斜面上
---可得知速度与竖直方向夹角a 。
物体从斜面上平抛又落回到斜面
---可得知位移与水平方向夹角a 。
---当合速度平行于斜面时,物体离斜面最远。
a
v0
v
v0
vy
a
V0
典型应用平抛与斜面:
利用速度方向的正切值求解
利用位移方向的正切值求解
1.由A点以水平速度v0 抛出小球,落在倾角为的斜面上的B点时,速度方向与斜面垂直,不计空气阻力,则速大小vB=__________ ,飞行时间t = __________ 。
A
B
v0 /sinθ
v0/gtanθ
a
b
s
s
h1
h2
c
如图为平抛运动轨迹的一部分,(抛出点未知)已知条件如图所示。
求该平抛运动初速度v0
应用:平抛初位置未知
抛体运动章末复习
抛 体 运 动
曲线运动
运动的合
成与分解
抛体运动的规律
速度方向
法则
沿曲线的切线方向
合力方向与速度方向不在同一条直线上
等时性、独立性、
等效性、同体性
化曲为直
平行四边形定则
知识结构
运动条件
研究方法
基本概念:合运动、分运动
分运动、合运动性质
分类:平抛运动、斜抛运动
水平方向:匀速直线运动
竖直方向:自由落体运动
2. 运动性质:
轨迹是曲线;运动方向时刻在改变是 ;一定具有加速度, 。
3、运动的条件:运动物体所受合外力方向跟它的速度方向 。
1.速度方向:做曲线运动的物体在某点速度方向是曲线在该点的 。
变速运动
合外力不为零
切线方向
不在同一直线上
4、轨迹特点:物体曲线运动的轨迹应在合力F与速度v方向之间,并且合力F指向 。
轨迹的内侧
一:曲线运动
1、速度变化的运动必是曲线运动吗?
2、加速度变化的运动必是曲线运动吗?
3、曲线运动一定是变速运动?
4、变速运动一定是曲线运动?
5、曲线运动的速度一定变?
6、做曲线运动的物体所受合力一定不为零?
7、物体在恒力下不可能做曲线运动?
8、物体在变力作用下一定做曲线运动?
9、加速度恒定的运动不可能是曲线运动?
错
错
错
错
错
错
对
对
对
练习1
1、基本概念:合运动:物体 ;
3、特点:
4、法则:
运动的合成具有惟一性,而运动的分解不惟一,通常按运动所产生的实际效果分解。
分运动:物体同时参与合成的运动的运动。
等时性、独立性、等效性、同体性
平行四边形定则(或三角形定则)
实际的运动
2、实质:运动的合成与分解是指 的合成与分解。
a、v、x
二:运动的合成与分解
1)是直线运动还是曲线运动?(判断轨迹)
2)是匀变速运动还是变加速运动?(判断运动性质)
判断:不在一直线上的两个匀速直线运动的合运动?一个匀速直线运动与一个匀加速直线运动的合运动?两个匀变速直线运动的合运动?
回忆:如何判断两个直线运动的合运动的运动轨迹和运动性质?
合力F合的方向或加速度a的方向与合速度v合的方向是否同一直线
合力或加速度是否恒定
几种运动的合成
1、两互成角度的匀速直线运动的合成
(一定是匀速直线运动)
V2
V1
V合
2、两互成角度的初速为零的匀加速直线运动的合成
(一定是匀加速直线运动)
V2
V合
V1
a合
a2
a1
3、两互成角度的初速不为零的匀加速直线运动的合成
(匀变速直线运动或匀变速曲线运动)
V2
V合
V1
a合
a2
a1
4、一个匀速直线运动和一个匀加速直线运动的合成
(匀变速直线运动或匀变速曲线运动)
V2
V合
a
V1
1.曲线运动一定是变速运动。
2.合运动的加速度为分运动的加速度矢量和。
3.如果做曲线运动的物体运动速度大小没有发生变化,则物体加速度为零。
4.物体在变力或恒力作用下都可能作直线运动。
5.物体所受的合外力方向与速度的方向不在同一条直线上,物体就作曲线运动。
6.静止物体在恒力作用下一定做匀加速直线运动。
7.物体受到多力作用而在做匀速运动,当撤去一个力时物体运动做匀变速运动。
8.平抛运动是匀变速曲线运动。
9.如果平抛物体运动时间足够长,则其速度方向将变为竖直向下。
10.向心加速度的物理意义是描述做圆周运动的质点向心力变化的快慢。
概念判断:
方法1.按运动的实际效果分解
方法2.正交分解
1)分解的原则
2)运动分解的典型问题
a.小船过河问题
b.关联速度问题
运动的分解
小船过河问题:
船速为v1 水速为v2
当v1 >v2
1)时间最短
2)位移最小
d
d
d
过河时间:
θ
v1
v2
v
?
沿绳方向的伸长或收缩运动
垂直于绳方向的旋转运动
则V与V1的关系为 ?
关联速度问题
“关联速度”问题解题关键:
1.沿绳(或杆)速度大小相同
2.物体实际的运动是合运动
3、处理方法:
2、性质:
化曲为直:
分解为水平方向的匀速直线运动和竖直方向的自由落体运动。
匀变速曲线运动
1、条件:
①具有 ;
② 。
水平的初速度
只受重力
三:抛体运动的规律
平抛运动
4、平抛运动速度和位移
VO
mg
o
x
y
vx
vy
v
t
①平抛物体在 t 时刻的瞬时速度:
水平方向:vx=vo
竖直方向:vy=gt
速度方向:(与水平方向夹角)
tan α =vy/vx=gt/vo
α
VO
mg
o
x
y
y
x
s
t
②平抛物体在 t 时刻的位移:
水平方向: x=vot
竖直方向:y=1/2gt2
位移方向:(与水平方向夹角)
tan?=y/x = gt/2vo
β
tan α =2 tan?
已知tan α =vy/vx=gt/vo
平抛运动任意时刻速度的反向延长线一定经过此时水平位移的中点
做平抛运动的物体垂直落在斜面上
---可得知速度与竖直方向夹角a 。
物体从斜面上平抛又落回到斜面
---可得知位移与水平方向夹角a 。
---当合速度平行于斜面时,物体离斜面最远。
a
v0
v
v0
vy
a
V0
典型应用平抛与斜面:
利用速度方向的正切值求解
利用位移方向的正切值求解
1.由A点以水平速度v0 抛出小球,落在倾角为的斜面上的B点时,速度方向与斜面垂直,不计空气阻力,则速大小vB=__________ ,飞行时间t = __________ 。
A
B
v0 /sinθ
v0/gtanθ
a
b
s
s
h1
h2
c
如图为平抛运动轨迹的一部分,(抛出点未知)已知条件如图所示。
求该平抛运动初速度v0
应用:平抛初位置未知
