5.2 运动的合成和分解(第二课时)25张PPT
文档属性
| 名称 | 5.2 运动的合成和分解(第二课时)25张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-02-22 00:00:00 | ||
图片预览







文档简介
人教版 必修 第二册
5.2运动的合成和分解
(第二课时)
问题
思考:如图,若你是船夫,有位客人需要渡河,要求快速过河,此时你该如何驾驶船只能使客人快速过河?
L
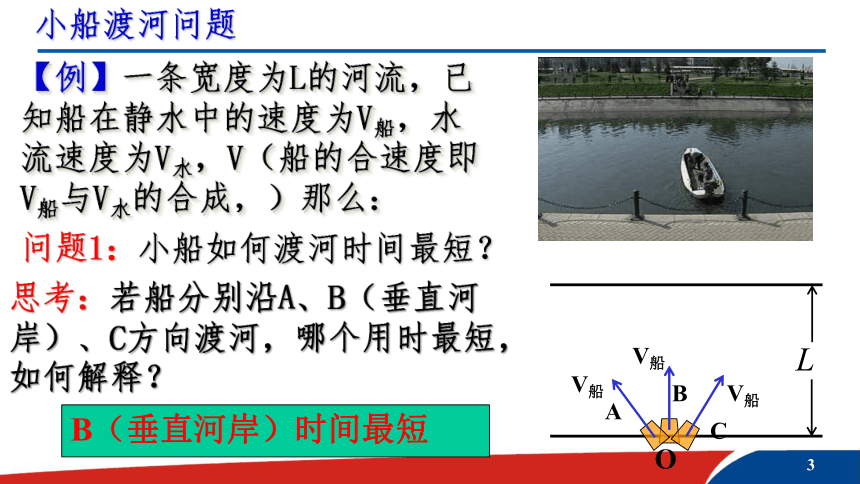
小船渡河问题
【例】一条宽度为L的河流,已知船在静水中的速度为V船,水流速度为V水,V(船的合速度即V船与V水的合成,)那么:
问题1:小船如何渡河时间最短?
思考:若船分别沿A、B(垂直河岸)、C方向渡河,哪个用时最短,如何解释?
V船
V船
V船
A
B
C
O
B(垂直河岸)时间最短
L
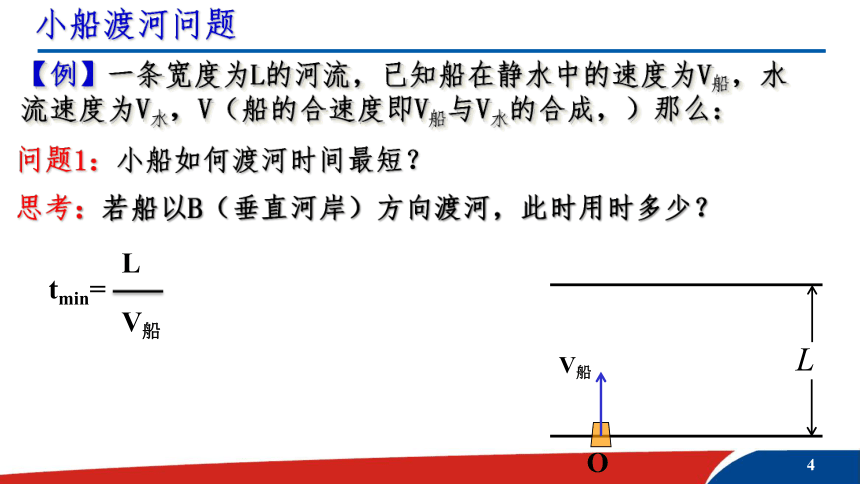
小船渡河问题
【例】一条宽度为L的河流,已知船在静水中的速度为V船,水流速度为V水,V(船的合速度即V船与V水的合成,)那么:
问题1:小船如何渡河时间最短?
思考:若船以B(垂直河岸)方向渡河,此时用时多少?
V船
O
tmin=
L
V船
L
小船渡河问题
【例】一条宽度为L的河流,已知船在静水中的速度为V船,水流速度为V水,V(船的合速度即V船与V水的合成,)那么:
问题1:小船如何渡河时间最短?
思考:若船以B(垂直河岸)方向渡河,此时船做什么运动?
V船
O
V水
V
思考:船的速度是多少?
匀速直线运动
V船
V=√(V船)2+(V水)2
L
小船渡河问题
【例】一条宽度为L的河流,已知船在静水中的速度为V船,水流速度为V水,V(船的合速度即V船与V水的合成,)那么:
问题1:小船如何渡河时间最短?
思考:若船以B(垂直河岸)方向渡河,船是如何到达对岸的?
V船
O
V水
V
沿右上方到达河对岸
L
小船渡河问题
【例】一条宽度为L的河流,已知船在静水中的速度为V船,水流速度为V水,V(船的合速度即V船与V水的合成,)那么:
问题1:小船如何渡河时间最短?
思考:若船以B(垂直河岸)方向渡河,此时船的位移是多少?
V船
O
V水
V
x
法一:
由x=vt得 x=vtmin
=√(V船)2+(V水)2
L
V船
L
小船渡河问题
【例】一条宽度为L的河流,已知船在静水中的速度为V船,水流速度为V水,V(船的合速度即V船与V水的合成,)那么:
问题1:小船如何渡河时间最短?
思考:若船以B(垂直河岸)方向渡河,此时船的位移是多少?
V船
O
V水
V
x
法二:
由几何关系得:
L
x
θ
V船
sinθ=
又:sinθ=
V船
V
小船在静水中速度为v,今小船要渡过一条小河,船在行驶过程中,船头始终与河岸垂直.若航行到河中间时,水流速度增大,则渡河时间与预定的时间相比( )
A.减少 B.不变
C.增加 D.无法确定
B
小船渡河问题
【例】一条宽度为L的河流,已知船在静水中的速度为V船,水流速度为V水,V(船的合速度即V船与V水的合成,)那么:
问题2:若V船>V水,怎样渡河位移最小?
L
v水
小船渡河问题
思考:若船分别到达河对岸A、B、C(C为O点正对岸)三个位置,
如何表示其位移?
C
A
B
O
C位置位移最短
到达哪个位置位移最短?
问题2:若V船>V水,怎样渡河位移最小?
L
v船
θ
小船渡河问题
思考:若船想到达河正对岸C位置,此时船头是正对河岸吗?
C
不是,船头应指向左上方与河岸有一定夹角
【例】一条宽度为L的河流,已知船在静水中的速度为V船,水流速度为V水,V(船的合速度即V船与V水的合成,)那么:
问题2:若V船>V水,怎样渡河位移最小?
L
v船
θ
v水
v
小船渡河问题
思考:船到达河正对岸C位置,此时船的合速度方向向哪?
C
合速度方向即船实际运动方向为O到C
【例】一条宽度为L的河流,已知船在静水中的速度为V船,水流速度为V水,V(船的合速度即V船与V水的合成,)那么:
问题2:若V船>V水,怎样渡河位移最小?
L
v船
θ
v水
v
小船渡河问题
思考:此时船合速度大小是多少?
C
v船
θ
cosθ=
V水
V船
sinθ=
V
V船
V=V船sinθ
【例】一条宽度为L的河流,已知船在静水中的速度为V船,水流速度为V水,V(船的合速度即V船与V水的合成,)那么:
问题2:若V船>V水,怎样渡河位移最小?
L
v水
v
小船渡河问题
思考:此时船渡河做什么运动?
C
匀速直线运动
v船
思考:此时船如何到达河对岸?
沿OC垂直到达河对岸
O
【例】一条宽度为L的河流,已知船在静水中的速度为V船,水流速度为V水,V(船的合速度即V船与V水的合成,)那么:
问题2:若V船>V水,怎样渡河位移最小?
L
v船
θ
v水
v
小船渡河问题
思考:此时船渡河需要多长时间?
C
v船
θ
由x=vt得
L
V船sinθ
=
【例】一条宽度为L的河流,已知船在静水中的速度为V船,水流速度为V水,V(船的合速度即V船与V水的合成,)那么:
问题3:若V船L
v水
小船渡河问题
O
不能
思考:此时船还能否垂直到达河对岸?
【例】一条宽度为L的河流,已知船在静水中的速度为V船,水流速度为V水,V(船的合速度即V船与V水的合成,)那么:
v船
问题3:若V船L
v水
小船渡河问题
O
【例】一条宽度为L的河流,已知船在静水中的速度为V船,水流速度为V水,V(船的合速度即V船与V水的合成,)那么:
v船
分析步骤
以v水箭头为圆心
以v船箭大小为半径做圆
从O点向圆做切线,其方向即为最小位移的合速度方向
V
把圆心与切点连接即为船头朝向
问题3:若V船L
v水
小船渡河问题
O
【例】一条宽度为L的河流,已知船在静水中的速度为V船,水流速度为V水,V(船的合速度即V船与V水的合成,)那么:
v船
V
α
思考:此时船如何到达河对岸?
v船
cosα=
V水
V船
思考:此时最短位移是多少?
α
Xmin
=
=
L
Xmin
即:
Xmin=
V水L
V船
问题3:若V船L
v水
小船渡河问题
O
【例】一条宽度为L的河流,已知船在静水中的速度为V船,水流速度为V水,V(船的合速度即V船与V水的合成,)那么:
v船
V
α
思考:此时船历时多久达河对岸?
v船
sinα=
V
V 水
V=V 水sinα
由x=vt得
L
V船sinα
=
河宽L=200 m,水速V水=2m/s,船在静水中的速度V船=4m/s,欲分别按下列要求过河时,船头应与河岸成多大角度?过河时间是多少?
(1)以最短时间过河;
(2)以最小位移过河;
课堂练习
(3)V水=5m/s,V船=4m/s以最小位移过河,
此时最小位移是多少?历时多久?
如图所示,纤绳以恒定速率v 沿水平方向通过定滑轮牵引小船靠岸,当纤绳与水面夹角为θ时,船靠岸的速度是__________.
关联速度问题分析
绳子末端速度的分解
(1)确定合运动(合速度)的方向(物体实际运动的方向)
(2)把合速度沿绳(杆)方向和垂直于绳(杆)方向分解
(3)根据沿绳(杆)方向的分速度大小相等,
利用三角函数等数学知识求解
分析思路
如图所示,纤绳以恒定速率v 沿水平方向通过定滑轮牵引小船靠岸,当纤绳与水面夹角为θ时,船靠岸的速度是____
_ .
关联速度分解问题
V船=_
课堂练习
θ
v1
v2
v
V1=VCOSθ
如图:小车向右做匀速直线运动,试分析物块做什么运动?绳的拉力与物体重力大小关系?
关联速度分解问题
5.2运动的合成和分解
(第二课时)
问题
思考:如图,若你是船夫,有位客人需要渡河,要求快速过河,此时你该如何驾驶船只能使客人快速过河?
L
小船渡河问题
【例】一条宽度为L的河流,已知船在静水中的速度为V船,水流速度为V水,V(船的合速度即V船与V水的合成,)那么:
问题1:小船如何渡河时间最短?
思考:若船分别沿A、B(垂直河岸)、C方向渡河,哪个用时最短,如何解释?
V船
V船
V船
A
B
C
O
B(垂直河岸)时间最短
L
小船渡河问题
【例】一条宽度为L的河流,已知船在静水中的速度为V船,水流速度为V水,V(船的合速度即V船与V水的合成,)那么:
问题1:小船如何渡河时间最短?
思考:若船以B(垂直河岸)方向渡河,此时用时多少?
V船
O
tmin=
L
V船
L
小船渡河问题
【例】一条宽度为L的河流,已知船在静水中的速度为V船,水流速度为V水,V(船的合速度即V船与V水的合成,)那么:
问题1:小船如何渡河时间最短?
思考:若船以B(垂直河岸)方向渡河,此时船做什么运动?
V船
O
V水
V
思考:船的速度是多少?
匀速直线运动
V船
V=√(V船)2+(V水)2
L
小船渡河问题
【例】一条宽度为L的河流,已知船在静水中的速度为V船,水流速度为V水,V(船的合速度即V船与V水的合成,)那么:
问题1:小船如何渡河时间最短?
思考:若船以B(垂直河岸)方向渡河,船是如何到达对岸的?
V船
O
V水
V
沿右上方到达河对岸
L
小船渡河问题
【例】一条宽度为L的河流,已知船在静水中的速度为V船,水流速度为V水,V(船的合速度即V船与V水的合成,)那么:
问题1:小船如何渡河时间最短?
思考:若船以B(垂直河岸)方向渡河,此时船的位移是多少?
V船
O
V水
V
x
法一:
由x=vt得 x=vtmin
=√(V船)2+(V水)2
L
V船
L
小船渡河问题
【例】一条宽度为L的河流,已知船在静水中的速度为V船,水流速度为V水,V(船的合速度即V船与V水的合成,)那么:
问题1:小船如何渡河时间最短?
思考:若船以B(垂直河岸)方向渡河,此时船的位移是多少?
V船
O
V水
V
x
法二:
由几何关系得:
L
x
θ
V船
sinθ=
又:sinθ=
V船
V
小船在静水中速度为v,今小船要渡过一条小河,船在行驶过程中,船头始终与河岸垂直.若航行到河中间时,水流速度增大,则渡河时间与预定的时间相比( )
A.减少 B.不变
C.增加 D.无法确定
B
小船渡河问题
【例】一条宽度为L的河流,已知船在静水中的速度为V船,水流速度为V水,V(船的合速度即V船与V水的合成,)那么:
问题2:若V船>V水,怎样渡河位移最小?
L
v水
小船渡河问题
思考:若船分别到达河对岸A、B、C(C为O点正对岸)三个位置,
如何表示其位移?
C
A
B
O
C位置位移最短
到达哪个位置位移最短?
问题2:若V船>V水,怎样渡河位移最小?
L
v船
θ
小船渡河问题
思考:若船想到达河正对岸C位置,此时船头是正对河岸吗?
C
不是,船头应指向左上方与河岸有一定夹角
【例】一条宽度为L的河流,已知船在静水中的速度为V船,水流速度为V水,V(船的合速度即V船与V水的合成,)那么:
问题2:若V船>V水,怎样渡河位移最小?
L
v船
θ
v水
v
小船渡河问题
思考:船到达河正对岸C位置,此时船的合速度方向向哪?
C
合速度方向即船实际运动方向为O到C
【例】一条宽度为L的河流,已知船在静水中的速度为V船,水流速度为V水,V(船的合速度即V船与V水的合成,)那么:
问题2:若V船>V水,怎样渡河位移最小?
L
v船
θ
v水
v
小船渡河问题
思考:此时船合速度大小是多少?
C
v船
θ
cosθ=
V水
V船
sinθ=
V
V船
V=V船sinθ
【例】一条宽度为L的河流,已知船在静水中的速度为V船,水流速度为V水,V(船的合速度即V船与V水的合成,)那么:
问题2:若V船>V水,怎样渡河位移最小?
L
v水
v
小船渡河问题
思考:此时船渡河做什么运动?
C
匀速直线运动
v船
思考:此时船如何到达河对岸?
沿OC垂直到达河对岸
O
【例】一条宽度为L的河流,已知船在静水中的速度为V船,水流速度为V水,V(船的合速度即V船与V水的合成,)那么:
问题2:若V船>V水,怎样渡河位移最小?
L
v船
θ
v水
v
小船渡河问题
思考:此时船渡河需要多长时间?
C
v船
θ
由x=vt得
L
V船sinθ
=
【例】一条宽度为L的河流,已知船在静水中的速度为V船,水流速度为V水,V(船的合速度即V船与V水的合成,)那么:
问题3:若V船
v水
小船渡河问题
O
不能
思考:此时船还能否垂直到达河对岸?
【例】一条宽度为L的河流,已知船在静水中的速度为V船,水流速度为V水,V(船的合速度即V船与V水的合成,)那么:
v船
问题3:若V船
v水
小船渡河问题
O
【例】一条宽度为L的河流,已知船在静水中的速度为V船,水流速度为V水,V(船的合速度即V船与V水的合成,)那么:
v船
分析步骤
以v水箭头为圆心
以v船箭大小为半径做圆
从O点向圆做切线,其方向即为最小位移的合速度方向
V
把圆心与切点连接即为船头朝向
问题3:若V船
v水
小船渡河问题
O
【例】一条宽度为L的河流,已知船在静水中的速度为V船,水流速度为V水,V(船的合速度即V船与V水的合成,)那么:
v船
V
α
思考:此时船如何到达河对岸?
v船
cosα=
V水
V船
思考:此时最短位移是多少?
α
Xmin
=
=
L
Xmin
即:
Xmin=
V水L
V船
问题3:若V船
v水
小船渡河问题
O
【例】一条宽度为L的河流,已知船在静水中的速度为V船,水流速度为V水,V(船的合速度即V船与V水的合成,)那么:
v船
V
α
思考:此时船历时多久达河对岸?
v船
sinα=
V
V 水
V=V 水sinα
由x=vt得
L
V船sinα
=
河宽L=200 m,水速V水=2m/s,船在静水中的速度V船=4m/s,欲分别按下列要求过河时,船头应与河岸成多大角度?过河时间是多少?
(1)以最短时间过河;
(2)以最小位移过河;
课堂练习
(3)V水=5m/s,V船=4m/s以最小位移过河,
此时最小位移是多少?历时多久?
如图所示,纤绳以恒定速率v 沿水平方向通过定滑轮牵引小船靠岸,当纤绳与水面夹角为θ时,船靠岸的速度是__________.
关联速度问题分析
绳子末端速度的分解
(1)确定合运动(合速度)的方向(物体实际运动的方向)
(2)把合速度沿绳(杆)方向和垂直于绳(杆)方向分解
(3)根据沿绳(杆)方向的分速度大小相等,
利用三角函数等数学知识求解
分析思路
如图所示,纤绳以恒定速率v 沿水平方向通过定滑轮牵引小船靠岸,当纤绳与水面夹角为θ时,船靠岸的速度是____
_ .
关联速度分解问题
V船=_
课堂练习
θ
v1
v2
v
V1=VCOSθ
如图:小车向右做匀速直线运动,试分析物块做什么运动?绳的拉力与物体重力大小关系?
关联速度分解问题
