8.2 重力势能 18张PPT
文档属性
| 名称 | 8.2 重力势能 18张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-02-22 00:00:00 | ||
图片预览






文档简介
第八章 机械能守恒定律
第2节 重力势能
质量相同的两物体,位置高的和位置低的,哪个物体重力势能大?两物体高度相同,质量大的和质量小的,哪个重力势能大?你认为重力势能的表达式应该是怎样的呢?
一、重力做功
WG=mg ? h=mgh1-mgh2
WG=mgl cosθ=mg ? h=mgh1-mgh2
甲图中质量为m的小球从A运动到B,重力做功:
乙图中质量为m的小球从A运动到B‘,重力做功:
拓展学习
极限思想
总结:重力做功的特点
物体运动是,重力对它做的功只跟它的起点和
终点的位置有关,而跟物体的运动的路径无关。
物体的重力mg与它所在位置的高度h的乘积“mgh”是一个具有特殊意义的物理量。
二、重力势能
1.定义:物体所受重力mg与所处高度h的乘积叫做物体的重力势能。用Ep表示。
2、表达式
Ep = mgh
3、单位:焦耳(J)(国际单位制)
4、重力势能是标量
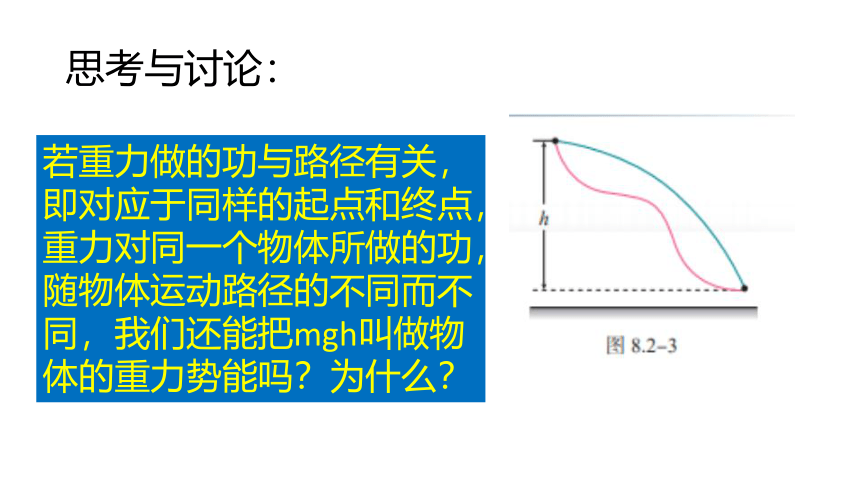
思考与讨论:
若重力做的功与路径有关,即对应于同样的起点和终点,重力对同一个物体所做的功,随物体运动路径的不同而不同,我们还能把mgh叫做物体的重力势能吗?为什么?
三、重力势能的相对性
重力势能具有相对性,为了比较势能的大小,应选同一个参考面,处在参考面的物体的重力势能为0 ,参考面上方的物体的重力势能是正数,参考面下方的物体的重力是负数。
重力势能的正负表示大小。
重力做功和重力势能变化的关系
1、当物体由高处向低处运动时:
重力做正功,即WG>0,EP1>EP2
重力势能减小
WG=-(EP2 -EP1 )
2、当物体由低处向高处运动时:
重力做负功,即WG<0,EP1<EP2
重力势能增大
例题1:
如图所示,质量为m的工件悬吊在水平操作台面上方,工件重心离地面的高度为h1,操作台面离地面的高度为h2,已知重力加速度为g,若选操作台面为零势能面,则工件的重力势能为( )
A.mgh1
B.mgh2
C.mg(h1-h2)
D.mg(h1+h2)
C
当堂训练1
质量相等的均质柔软细绳A、B平放于水平地面,绳A较长。分别捏住两绳中点缓慢提起,直到全部离开地面,两绳中点被提升的高度分别为hA、hB,上述过程中克服重力做的功分别为WA、WB。若( )。
A.hA=hB,则一定有WA=WB
B.hA>hB,则可能有WAC.hAD.hA>hB,则一定有WA>WB
B
B
四、弹性势能
拉长或压缩的弹簧、卷紧的发条、拉开的弓、正在击球的网球拍、撑竿跳高运动员手中弯曲的竿(图8.2-6),等等,这些物体都发生了弹性形变,每个物体的各部分之间都有弹力的相互作用。发生弹性形变的物体的各部分之间,由于有弹力的相互作用,也具有势能,这种势能叫作弹性势能(elastic potential energy)
探究:弹性势能的大小和弹力做功的关系
Ⅰ.物体的弹性势能跟哪些因素有关?
1、弹簧的形变量
2、劲度系数
1、拉伸过程的弹簧弹力是恒力还是变力?
F弹=kl
2、怎样求解变力做功?
微元法
3、怎样由拉力做功得出弹性势能表达式?
问题与思考
找出弹力做功的计算方法,再根据弹力做功与弹性势能的关系导出弹性势能的表达式。
弹性势能表达式
W拉= F拉 l
W拉= △EP
例题2
如图所示,将一木块放在弹簧上,用手压木块,弹簧被压缩。松开手,木块竖直向上飞起直到最高点。下列说法正确的是( )
A.手压木块时,手对木块的压力与弹簧对其支持力是一对平衡力B.弹簧恢复原状过程中,弹性势能先增大后减小C.松手后,木块在没有离开弹簧前,所受弹力方向竖直向下D.松手后,木块在没有离开弹簧前,所受弹力和木块对弹簧的压力总是大小相等
D
当堂训练2
如图所示,轻质弹簧的一端与内壁光滑的试管底部连接,另一端连接质量为m的小球,小球的直径略小于试管的内径,开始时试管位于水平面静止,弹簧处于原长,小球也静止,若缓慢增大试管的倾角θ至试管竖直,弹簧始终在弹性限度内,则下列说法中正确的是( )
A.整个过程中弹性势能一定逐渐增大B.整个过程中弹性势能可能先增大后减小C.整个过程中小球重力势能一定逐渐增大D.整个过程中小球重力势能可能先增大后减小
AD
第2节 重力势能
质量相同的两物体,位置高的和位置低的,哪个物体重力势能大?两物体高度相同,质量大的和质量小的,哪个重力势能大?你认为重力势能的表达式应该是怎样的呢?
一、重力做功
WG=mg ? h=mgh1-mgh2
WG=mgl cosθ=mg ? h=mgh1-mgh2
甲图中质量为m的小球从A运动到B,重力做功:
乙图中质量为m的小球从A运动到B‘,重力做功:
拓展学习
极限思想
总结:重力做功的特点
物体运动是,重力对它做的功只跟它的起点和
终点的位置有关,而跟物体的运动的路径无关。
物体的重力mg与它所在位置的高度h的乘积“mgh”是一个具有特殊意义的物理量。
二、重力势能
1.定义:物体所受重力mg与所处高度h的乘积叫做物体的重力势能。用Ep表示。
2、表达式
Ep = mgh
3、单位:焦耳(J)(国际单位制)
4、重力势能是标量
思考与讨论:
若重力做的功与路径有关,即对应于同样的起点和终点,重力对同一个物体所做的功,随物体运动路径的不同而不同,我们还能把mgh叫做物体的重力势能吗?为什么?
三、重力势能的相对性
重力势能具有相对性,为了比较势能的大小,应选同一个参考面,处在参考面的物体的重力势能为0 ,参考面上方的物体的重力势能是正数,参考面下方的物体的重力是负数。
重力势能的正负表示大小。
重力做功和重力势能变化的关系
1、当物体由高处向低处运动时:
重力做正功,即WG>0,EP1>EP2
重力势能减小
WG=-(EP2 -EP1 )
2、当物体由低处向高处运动时:
重力做负功,即WG<0,EP1<EP2
重力势能增大
例题1:
如图所示,质量为m的工件悬吊在水平操作台面上方,工件重心离地面的高度为h1,操作台面离地面的高度为h2,已知重力加速度为g,若选操作台面为零势能面,则工件的重力势能为( )
A.mgh1
B.mgh2
C.mg(h1-h2)
D.mg(h1+h2)
C
当堂训练1
质量相等的均质柔软细绳A、B平放于水平地面,绳A较长。分别捏住两绳中点缓慢提起,直到全部离开地面,两绳中点被提升的高度分别为hA、hB,上述过程中克服重力做的功分别为WA、WB。若( )。
A.hA=hB,则一定有WA=WB
B.hA>hB,则可能有WA
B
B
四、弹性势能
拉长或压缩的弹簧、卷紧的发条、拉开的弓、正在击球的网球拍、撑竿跳高运动员手中弯曲的竿(图8.2-6),等等,这些物体都发生了弹性形变,每个物体的各部分之间都有弹力的相互作用。发生弹性形变的物体的各部分之间,由于有弹力的相互作用,也具有势能,这种势能叫作弹性势能(elastic potential energy)
探究:弹性势能的大小和弹力做功的关系
Ⅰ.物体的弹性势能跟哪些因素有关?
1、弹簧的形变量
2、劲度系数
1、拉伸过程的弹簧弹力是恒力还是变力?
F弹=kl
2、怎样求解变力做功?
微元法
3、怎样由拉力做功得出弹性势能表达式?
问题与思考
找出弹力做功的计算方法,再根据弹力做功与弹性势能的关系导出弹性势能的表达式。
弹性势能表达式
W拉= F拉 l
W拉= △EP
例题2
如图所示,将一木块放在弹簧上,用手压木块,弹簧被压缩。松开手,木块竖直向上飞起直到最高点。下列说法正确的是( )
A.手压木块时,手对木块的压力与弹簧对其支持力是一对平衡力B.弹簧恢复原状过程中,弹性势能先增大后减小C.松手后,木块在没有离开弹簧前,所受弹力方向竖直向下D.松手后,木块在没有离开弹簧前,所受弹力和木块对弹簧的压力总是大小相等
D
当堂训练2
如图所示,轻质弹簧的一端与内壁光滑的试管底部连接,另一端连接质量为m的小球,小球的直径略小于试管的内径,开始时试管位于水平面静止,弹簧处于原长,小球也静止,若缓慢增大试管的倾角θ至试管竖直,弹簧始终在弹性限度内,则下列说法中正确的是( )
A.整个过程中弹性势能一定逐渐增大B.整个过程中弹性势能可能先增大后减小C.整个过程中小球重力势能一定逐渐增大D.整个过程中小球重力势能可能先增大后减小
AD
