2020—2021学年人教版九年级数学下册第27章相似常考题型综合练习四(word版含答案)
文档属性
| 名称 | 2020—2021学年人教版九年级数学下册第27章相似常考题型综合练习四(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 134.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 14:18:43 | ||
图片预览



文档简介
九年级数学下册第27章《相似》常考题型综合练习四
1.如图,已知AC,EC分别为正方形ABCD和正方形EFCG的对角线,点E在△ABC内,连接BF,∠CAE+∠CBE=90°.
(1)求证:△CAE∽△CBF;
(2)若BE=1,AE=2,求CE的长.
2.如图,在等腰三角形ABC中,AB=AC,D是AB边上一点,以CD为一边,向上作等腰△DCE,使△EDC∽△ABC,连AE,求证:
(1)∠BCD=∠ACE;
(2)AE∥BC.
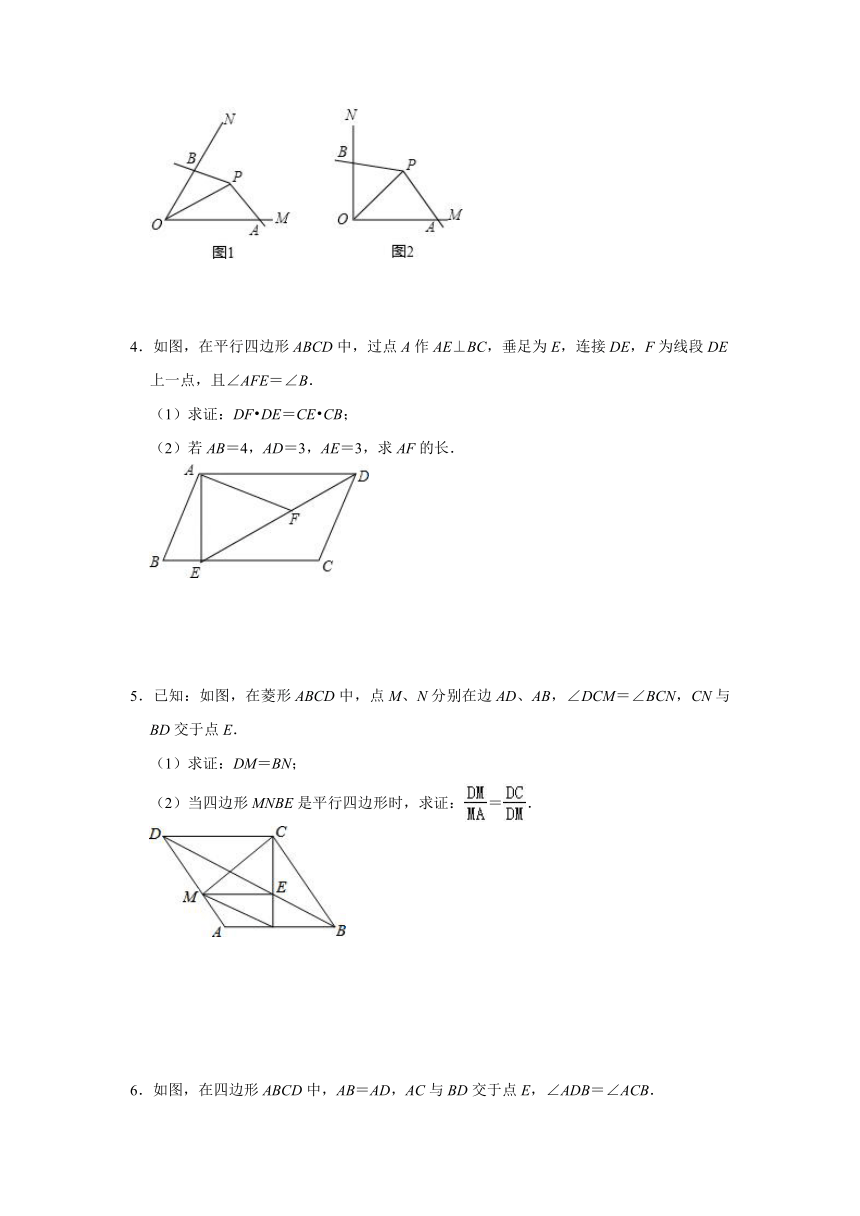
3.如图1,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,如果∠APB绕点P旋转时始终满足OA?OB=OP2,我们就把∠APB叫做∠MON的智慧角.如图2,已知∠MON=90°,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,且∠APB=135°.
请判断:∠APB是否为∠MON的智慧角,并说明理由.
4.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:DF?DE=CE?CB;
(2)若AB=4,AD=3,AE=3,求AF的长.
5.已知:如图,在菱形ABCD中,点M、N分别在边AD、AB,∠DCM=∠BCN,CN与BD交于点E.
(1)求证:DM=BN;
(2)当四边形MNBE是平行四边形时,求证:=.
6.如图,在四边形ABCD中,AB=AD,AC与BD交于点E,∠ADB=∠ACB.
(1)求证:△ABE∽△ACB;
(2)若AB⊥AC,AE:EC=1:2,求∠ABC的度数.
7.菱形ABCD中,∠BAD是锐角,AC,BD相交于点O,E是BD的延长线上一动点(不与点D重合),连接EC并延长和AB的延长线交于点F,连接AE.
(1)比较∠F和∠ABD的大小,并说明理由;
(2)当△BFC有一个内角是直角时,求证:△BFC∽△EFA;
(3)当△BFC与△EFA相似(两三角形的公共角为对应角),且AC=12,DE=5时,求△BFC与△EFA的相似比.
8.如图,在矩形纸片ABCD中,AB=3,BC=4.把△BCD沿对角线BD折叠,使点C落在E处,BE交AD于点F;
(1)求证:AF=EF;
(2)求tan∠ABF的值;
(3)连接AC交BE于点G,求AG的长.
9.如图,以△ABC的边BC为弦,在点A的同侧画交AB于D,且∠BDC=90°+∠A,点P是上的一个动点.
(1)判定△ADC的形状,并说明理由;
(2)若∠A=70°,当点P运动到∠PBA=∠PBC=15°时,求∠ACB和∠ACP的度数.
(3)当点P在上运动时,过点P画直线MN⊥AP,分别交AB、AC于点M、N,是否存在这样的点P,使得△BMP和△BPC和△CPN彼此相似?请说明理由.
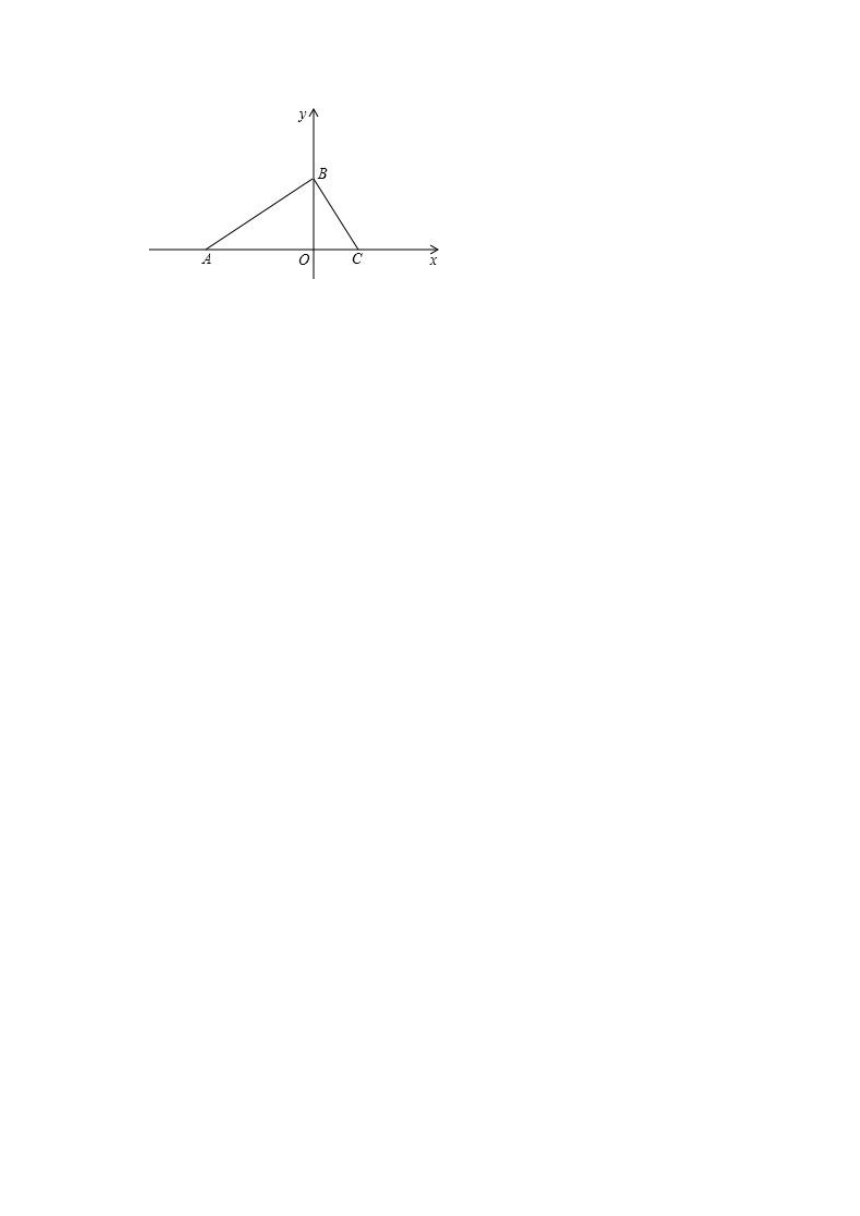
10.已知:如图,在平面直角坐标系中,点A、B的坐标分别为A(﹣4,0),B(0,3).
(1)求AB的长;
(2)过点B作BC⊥AB,交轴于点C,求点C的坐标;
(3)在(2)的条件下,如果P、Q分别是AB和AC上的动点,连接PQ,设AP=CQ=x,问是否存在这样的使得△APQ与△ABC相似?若存在,请求出的x值;若不存在,请说明理由.
参考答案
1.(1)证明:∵四边形ABCD和EFCG均为正方形,
∴==,
∴∠ACB=∠ECF=45°,
∴∠ACE=∠BCF,
∴△CAE∽△CBF.
(2)解:∵△CAE∽△CBF,
∴∠CAE=∠△CBF,=,
又∵∠CAE+∠CBE=90°,
∴∠CBF+∠CBE=90°,
∴∠EBF=90°,
又∵==,AE=2
∴=,
∴BF=,
∴EF2=BE2+BF2=3,
∴EF=,
∵CE2=2EF2=6,
∴CE=.
2.证明(1)∵△EDC∽△ABC,
∴∠ECD=∠ACB,
∴∠BCD=∠ACE;
(2)由(1)知∠BCD=∠ACE,
∵△ABC∽△EDC,
∴=,
∴△BCD∽△ACE
∴∠CAE=∠B,
∴∠CAE=∠ACB,
∴AE∥BC.
3.证明:∵∠MON=90°,P为∠MON的平分线上一点,
∴∠AOP=∠BOP=∠MON=45°,
∵∠AOP+∠OAP+∠APO=180°,
∴∠OAP+∠APO=135°,
∵∠APB=135°,
∴∠APO+∠OPB=135°,
∴∠OAP=∠OPB,
∴△AOP∽△POB,
∴,
∴OP2=OA?OB,
∴∠APB是∠MON的智慧角.
4.(1)证明:∵平行四边形ABCD,∠AFE=∠B,
∴AB∥CD,AD∥BC,AD=BC,
∴∠B+∠C=180°,∠ADF=∠CED,
∵∠AFD+∠AFE=180°,
∴∠C=∠AFD,
∴△ADF∽△DEC,
∴=,即DF?DE=CE?AD,
则DF?DE=CE?CB;
(2)解:∵AE⊥BC,
∴∠AEB=∠AEC=90°,
在Rt△ADE中,根据勾股定理得:DE==3,
∵△ADF∽△DEC,
∴=,即=,
解得:AF=2.
5.(1)证明:在菱形ABCD中,
∵CD=BC,∠CDM=∠CBN,
在△CDM与△CBN中,,
∴△CDM≌△CBN,
∴DM=BN;
(2)解:∵四边形MNBE是平行四边形,
∴ME∥AB,
∴,
∵DC∥AB
∴△CDE∽△NBE,
∴=,
∴,
∵DM=NB,
∴=.
6.证明:(1)∵AB=AD,
∴∠ADB=∠ABE,
又∵∠ADB=∠ACB,
∴∠ABE=∠ACB,
又∵∠BAE=∠CAB,
∴△ABE∽△ACB;
(2)设AE=x,
∵AE:EC=1:2,
∴EC=2x,
由(1)得:△ABE∽△ACB,
∴,
∴AB2=AE?AC,即AB2=x?3x
∴AB=x,
又∵BA⊥AC,
∴BC=2x,
∴∠ACB=30°,
∵F是BC中点,
∴BF=x,
∴BF=AB=AD,
连接AF,则AF=BF=CF,∠ACB=30°,
∴∠ABC=60°.
7.解:(1)∵∠ABD为△BFE的一个外角,
∴∠ABD>∠F;
(2)∵四边形ABCD是菱形,
∴BC∥AD,∠ABD=∠ABC,
∴∠BAD=∠FBC,∠BAD+∠ABC=180°
又∵∠BAD为锐角,
∴∠FBC为锐角,∠ABC为钝角,
∴∠ABD为锐角,
由(1)得:∠F也为锐角,
又∵△BFC有一个角是直角,
∴∠BCF为直角,
∵在△ABE和△CBE中,
∴△ABE≌△CBE,
∴∠BAE=∠BCE=90°,
∴∠FCB=∠FAE=90°,
∴△BFC∽△EFA.
(3)当△BFC与△EFA相似(两三角形的公共角为对应角)时
∵∠BCE为△BFC的外角,
∴∠BCE>∠FBC,∠BCE>∠F,
∴∠BAE=∠BCF=∠BCE=90°,∠FBC=∠AEF,
∴∠OAD=∠OEA
∴△OAD∽△OEA,
∴AO2=OD×OE,
设OD=x,列方程得:36=x(x+5),
解得:x=4,
∴BC:AE=AD:AE=AO:OE=2:3.
8.(1)证明:∵△EBD是由△CBD折叠而得,
∴ED=DC,BE=BC,
∵四边形ABCD是矩形,
∴AB=CD,∠BAD=∠BED=90°,
∴ED=AB,
∴∠ABF=∠EDF,
∵在△AFB与△EFD中,
,
∴△AFB≌△EFD(ASA),
∴AF=EF;
(2)解:设AF=x,
∵AB=3,BC=BE=4,AF=EF
∴BF=4﹣x,
∵∠BAF=90°
∴AF2+AB2=BF2,
∴x2+32=(4﹣x)2,
∴x=,
∴tan∠ABF===;
(3)解:∵四边形ABCD是矩形,
∴∠BAD=90°,AD∥BC;
∴AC===5,
∴△AGF∽△CGB,
∴=,
设AG=m,则CG=5﹣m,
∴=,
解得m=,即AG=.
9.解:(1)∵△ADC是等腰三角形.
∵∠BDC=,
∴∠ADC=,
∴∠ACD=﹣∠A=,
∴∠ACD=∠ADC,
∴△ADC是等腰三角形.
(2)∵∠A=70°,∠PBA=∠PBC=15°,
∴∠ACB=180°﹣70°﹣2×15°=80°,
∵∠BPC=∠BDC=,
∴∠PCB=180°﹣15°﹣125°=40°,
∴∠ACP=∠ACB﹣∠PCB=80°﹣40°=40°.
答:∠ACB为80°,∠ACP为40°.
(3)当点P运动至的中点时,△BMP和△BPC和△CPN彼此相似.
∵P运动至的中点,
∴∠ABP=∠CBP,
设∠A=x度,∠ABP=∠CBP=y度,
∴∠PCB=180﹣y﹣()=90﹣y﹣,
∵∠ACB=180﹣x﹣2y,
∴∠ACP=∠ACB﹣∠PCB=(180﹣x﹣2y)﹣(90﹣y﹣)=90﹣y﹣,
∴∠PCB=∠ACP,
∴PC平分∠ACB.
∴当点P运动至的中点时,点P是△ABC的角平分线的交点.
∴AP平分∠BAC.
∴∠BMP=∠CNP=90+=∠BPC,
∴△BMP和△BPC和△CPN彼此相似.
10.解:(1)∵点A、B的坐标分别为A(﹣4,0),B(0,3),
∴OB=3,AO=4,
∴AB==5;
(2)∵BC⊥AB,BO⊥AC,
∴BO2=AO?OC,即OC===2.25,
∴C点的坐标是(2.25,0);
(3)
当△APQ与∽△ABC时,PQ∥BC,
∴=,
∵AP=CQ=x,
∴=,
解得x=.
当△APQ与∽△ACB时,,
即,
解得:x=
答:(1)AB的长为5;(2)C的坐标为(2.25,0);(3)存在,x的值为或.
1.如图,已知AC,EC分别为正方形ABCD和正方形EFCG的对角线,点E在△ABC内,连接BF,∠CAE+∠CBE=90°.
(1)求证:△CAE∽△CBF;
(2)若BE=1,AE=2,求CE的长.
2.如图,在等腰三角形ABC中,AB=AC,D是AB边上一点,以CD为一边,向上作等腰△DCE,使△EDC∽△ABC,连AE,求证:
(1)∠BCD=∠ACE;
(2)AE∥BC.
3.如图1,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,如果∠APB绕点P旋转时始终满足OA?OB=OP2,我们就把∠APB叫做∠MON的智慧角.如图2,已知∠MON=90°,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,且∠APB=135°.
请判断:∠APB是否为∠MON的智慧角,并说明理由.
4.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:DF?DE=CE?CB;
(2)若AB=4,AD=3,AE=3,求AF的长.
5.已知:如图,在菱形ABCD中,点M、N分别在边AD、AB,∠DCM=∠BCN,CN与BD交于点E.
(1)求证:DM=BN;
(2)当四边形MNBE是平行四边形时,求证:=.
6.如图,在四边形ABCD中,AB=AD,AC与BD交于点E,∠ADB=∠ACB.
(1)求证:△ABE∽△ACB;
(2)若AB⊥AC,AE:EC=1:2,求∠ABC的度数.
7.菱形ABCD中,∠BAD是锐角,AC,BD相交于点O,E是BD的延长线上一动点(不与点D重合),连接EC并延长和AB的延长线交于点F,连接AE.
(1)比较∠F和∠ABD的大小,并说明理由;
(2)当△BFC有一个内角是直角时,求证:△BFC∽△EFA;
(3)当△BFC与△EFA相似(两三角形的公共角为对应角),且AC=12,DE=5时,求△BFC与△EFA的相似比.
8.如图,在矩形纸片ABCD中,AB=3,BC=4.把△BCD沿对角线BD折叠,使点C落在E处,BE交AD于点F;
(1)求证:AF=EF;
(2)求tan∠ABF的值;
(3)连接AC交BE于点G,求AG的长.
9.如图,以△ABC的边BC为弦,在点A的同侧画交AB于D,且∠BDC=90°+∠A,点P是上的一个动点.
(1)判定△ADC的形状,并说明理由;
(2)若∠A=70°,当点P运动到∠PBA=∠PBC=15°时,求∠ACB和∠ACP的度数.
(3)当点P在上运动时,过点P画直线MN⊥AP,分别交AB、AC于点M、N,是否存在这样的点P,使得△BMP和△BPC和△CPN彼此相似?请说明理由.
10.已知:如图,在平面直角坐标系中,点A、B的坐标分别为A(﹣4,0),B(0,3).
(1)求AB的长;
(2)过点B作BC⊥AB,交轴于点C,求点C的坐标;
(3)在(2)的条件下,如果P、Q分别是AB和AC上的动点,连接PQ,设AP=CQ=x,问是否存在这样的使得△APQ与△ABC相似?若存在,请求出的x值;若不存在,请说明理由.
参考答案
1.(1)证明:∵四边形ABCD和EFCG均为正方形,
∴==,
∴∠ACB=∠ECF=45°,
∴∠ACE=∠BCF,
∴△CAE∽△CBF.
(2)解:∵△CAE∽△CBF,
∴∠CAE=∠△CBF,=,
又∵∠CAE+∠CBE=90°,
∴∠CBF+∠CBE=90°,
∴∠EBF=90°,
又∵==,AE=2
∴=,
∴BF=,
∴EF2=BE2+BF2=3,
∴EF=,
∵CE2=2EF2=6,
∴CE=.
2.证明(1)∵△EDC∽△ABC,
∴∠ECD=∠ACB,
∴∠BCD=∠ACE;
(2)由(1)知∠BCD=∠ACE,
∵△ABC∽△EDC,
∴=,
∴△BCD∽△ACE
∴∠CAE=∠B,
∴∠CAE=∠ACB,
∴AE∥BC.
3.证明:∵∠MON=90°,P为∠MON的平分线上一点,
∴∠AOP=∠BOP=∠MON=45°,
∵∠AOP+∠OAP+∠APO=180°,
∴∠OAP+∠APO=135°,
∵∠APB=135°,
∴∠APO+∠OPB=135°,
∴∠OAP=∠OPB,
∴△AOP∽△POB,
∴,
∴OP2=OA?OB,
∴∠APB是∠MON的智慧角.
4.(1)证明:∵平行四边形ABCD,∠AFE=∠B,
∴AB∥CD,AD∥BC,AD=BC,
∴∠B+∠C=180°,∠ADF=∠CED,
∵∠AFD+∠AFE=180°,
∴∠C=∠AFD,
∴△ADF∽△DEC,
∴=,即DF?DE=CE?AD,
则DF?DE=CE?CB;
(2)解:∵AE⊥BC,
∴∠AEB=∠AEC=90°,
在Rt△ADE中,根据勾股定理得:DE==3,
∵△ADF∽△DEC,
∴=,即=,
解得:AF=2.
5.(1)证明:在菱形ABCD中,
∵CD=BC,∠CDM=∠CBN,
在△CDM与△CBN中,,
∴△CDM≌△CBN,
∴DM=BN;
(2)解:∵四边形MNBE是平行四边形,
∴ME∥AB,
∴,
∵DC∥AB
∴△CDE∽△NBE,
∴=,
∴,
∵DM=NB,
∴=.
6.证明:(1)∵AB=AD,
∴∠ADB=∠ABE,
又∵∠ADB=∠ACB,
∴∠ABE=∠ACB,
又∵∠BAE=∠CAB,
∴△ABE∽△ACB;
(2)设AE=x,
∵AE:EC=1:2,
∴EC=2x,
由(1)得:△ABE∽△ACB,
∴,
∴AB2=AE?AC,即AB2=x?3x
∴AB=x,
又∵BA⊥AC,
∴BC=2x,
∴∠ACB=30°,
∵F是BC中点,
∴BF=x,
∴BF=AB=AD,
连接AF,则AF=BF=CF,∠ACB=30°,
∴∠ABC=60°.
7.解:(1)∵∠ABD为△BFE的一个外角,
∴∠ABD>∠F;
(2)∵四边形ABCD是菱形,
∴BC∥AD,∠ABD=∠ABC,
∴∠BAD=∠FBC,∠BAD+∠ABC=180°
又∵∠BAD为锐角,
∴∠FBC为锐角,∠ABC为钝角,
∴∠ABD为锐角,
由(1)得:∠F也为锐角,
又∵△BFC有一个角是直角,
∴∠BCF为直角,
∵在△ABE和△CBE中,
∴△ABE≌△CBE,
∴∠BAE=∠BCE=90°,
∴∠FCB=∠FAE=90°,
∴△BFC∽△EFA.
(3)当△BFC与△EFA相似(两三角形的公共角为对应角)时
∵∠BCE为△BFC的外角,
∴∠BCE>∠FBC,∠BCE>∠F,
∴∠BAE=∠BCF=∠BCE=90°,∠FBC=∠AEF,
∴∠OAD=∠OEA
∴△OAD∽△OEA,
∴AO2=OD×OE,
设OD=x,列方程得:36=x(x+5),
解得:x=4,
∴BC:AE=AD:AE=AO:OE=2:3.
8.(1)证明:∵△EBD是由△CBD折叠而得,
∴ED=DC,BE=BC,
∵四边形ABCD是矩形,
∴AB=CD,∠BAD=∠BED=90°,
∴ED=AB,
∴∠ABF=∠EDF,
∵在△AFB与△EFD中,
,
∴△AFB≌△EFD(ASA),
∴AF=EF;
(2)解:设AF=x,
∵AB=3,BC=BE=4,AF=EF
∴BF=4﹣x,
∵∠BAF=90°
∴AF2+AB2=BF2,
∴x2+32=(4﹣x)2,
∴x=,
∴tan∠ABF===;
(3)解:∵四边形ABCD是矩形,
∴∠BAD=90°,AD∥BC;
∴AC===5,
∴△AGF∽△CGB,
∴=,
设AG=m,则CG=5﹣m,
∴=,
解得m=,即AG=.
9.解:(1)∵△ADC是等腰三角形.
∵∠BDC=,
∴∠ADC=,
∴∠ACD=﹣∠A=,
∴∠ACD=∠ADC,
∴△ADC是等腰三角形.
(2)∵∠A=70°,∠PBA=∠PBC=15°,
∴∠ACB=180°﹣70°﹣2×15°=80°,
∵∠BPC=∠BDC=,
∴∠PCB=180°﹣15°﹣125°=40°,
∴∠ACP=∠ACB﹣∠PCB=80°﹣40°=40°.
答:∠ACB为80°,∠ACP为40°.
(3)当点P运动至的中点时,△BMP和△BPC和△CPN彼此相似.
∵P运动至的中点,
∴∠ABP=∠CBP,
设∠A=x度,∠ABP=∠CBP=y度,
∴∠PCB=180﹣y﹣()=90﹣y﹣,
∵∠ACB=180﹣x﹣2y,
∴∠ACP=∠ACB﹣∠PCB=(180﹣x﹣2y)﹣(90﹣y﹣)=90﹣y﹣,
∴∠PCB=∠ACP,
∴PC平分∠ACB.
∴当点P运动至的中点时,点P是△ABC的角平分线的交点.
∴AP平分∠BAC.
∴∠BMP=∠CNP=90+=∠BPC,
∴△BMP和△BPC和△CPN彼此相似.
10.解:(1)∵点A、B的坐标分别为A(﹣4,0),B(0,3),
∴OB=3,AO=4,
∴AB==5;
(2)∵BC⊥AB,BO⊥AC,
∴BO2=AO?OC,即OC===2.25,
∴C点的坐标是(2.25,0);
(3)
当△APQ与∽△ABC时,PQ∥BC,
∴=,
∵AP=CQ=x,
∴=,
解得x=.
当△APQ与∽△ACB时,,
即,
解得:x=
答:(1)AB的长为5;(2)C的坐标为(2.25,0);(3)存在,x的值为或.
