2020—2021学年人教版数学八年级下册 18.2.1 矩形——矩形的性质与判定综合 随堂练习(word版含答案)
文档属性
| 名称 | 2020—2021学年人教版数学八年级下册 18.2.1 矩形——矩形的性质与判定综合 随堂练习(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 102.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-22 22:54:09 | ||
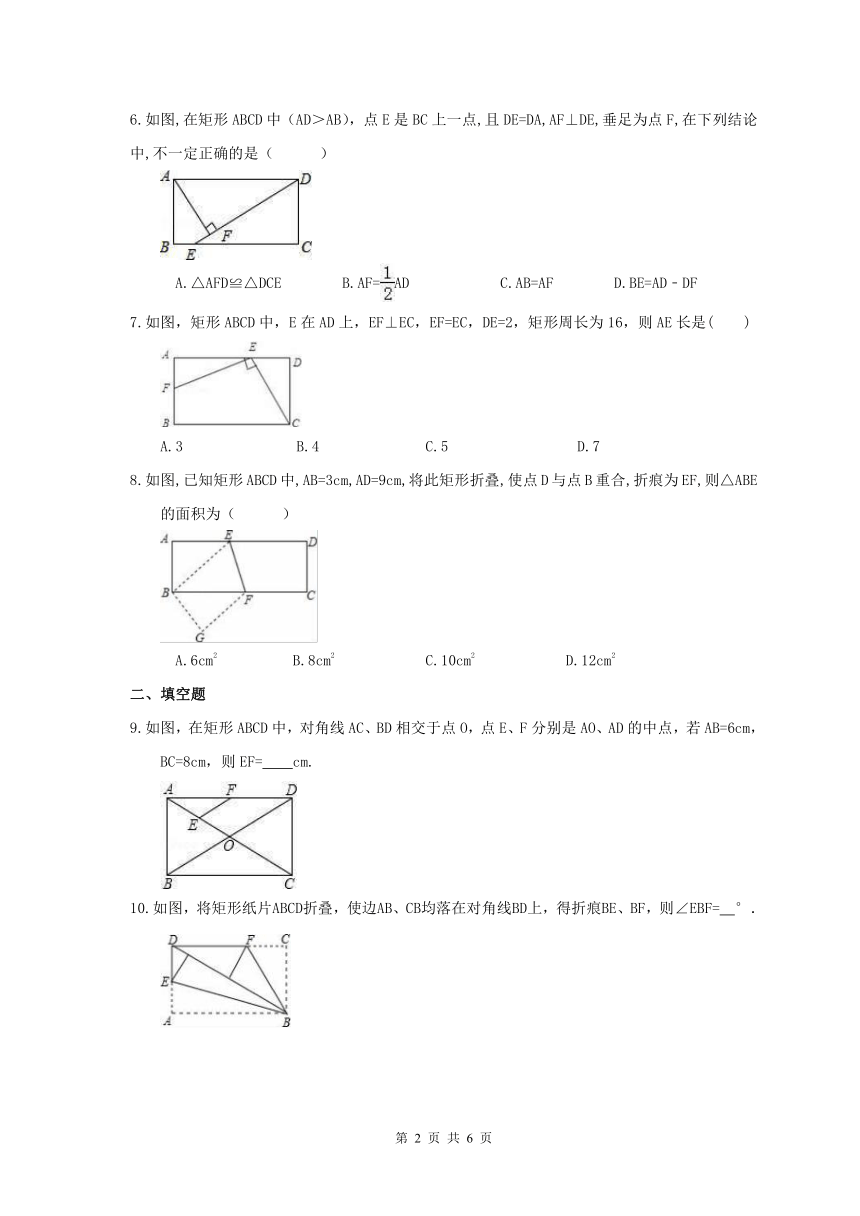
图片预览


文档简介
2021年人教版数学八年级下册《矩形的性质与判定综合》
随堂练习
一、选择题
1.如图,将矩形纸片ABCD沿对角线BD折叠一次,则图中全等三角形有(??? )
A.2对?? ?? B. 3对?? C. 4对??? D.5对
2.Rt△ABC中,∠C=90°,锐角为30°,最短边长为5cm,则最长边上的中线是( )
A.5cm B.15cm C.10cm D.2.5cm
3.如图,在矩形ABCD中,DE平分∠ADC交BC于点E,EF⊥AD交AD于点F,若EF=3,AE=5,则AD等于( )
A.5 B.6 C.7 D.8
4.如图,矩形ABCD的顶点A、C分别在直线a、b上,且a∥b,∠1=60°,则∠2的度数为( )
A.30° B.45° C.60° D.75°
5.如图,把矩形纸片ABCD纸沿对角线折叠,设重叠部分为△EBD,那么下列说法错误的是( )
A.△EBD是等腰三角形,EB=ED B.折叠后∠ABE和∠CBD一定相等
C.折叠后得到的图形是轴对称图形 D.△EBA和△EDC一定是全等三角形
6.如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )
A.△AFD≌△DCE B.AF=AD C.AB=AF D.BE=AD﹣DF
7.如图,矩形ABCD中,E在AD上,EF⊥EC,EF=EC,DE=2,矩形周长为16,则AE长是( )
A.3??? B.4?? ? C.5??? D.7
8.如图,已知矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点D与点B重合,折痕为EF,则△ABE的面积为( )
A.6cm2 B.8cm2 C.10cm2 D.12cm2
二、填空题
9.如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,则EF= cm.
10.如图,将矩形纸片ABCD折叠,使边AB、CB均落在对角线BD上,得折痕BE、BF,则∠EBF= °.
11.如图,在矩形ABCD中,AE⊥BD于E,∠DAE=3∠EAB,则∠ACD的度数为 .
12.如图是叠放在一起的两张长方形卡片,图中有∠1、∠2、∠3,则其中一定相等的是_____
13.将一张长方形纸片折叠成如图所示的形状,若∠DBC=56°,则∠1= °.
14.如图,在矩形ABCD中,AB=10,AD=6,E为BC上一点,把△CDE沿DE折叠,使点C落在AB边上的F处,则CE的长为 ?? .
三、解答题
15.如图,已知在矩形ABCD中,E、F分别是边BC、AB上的点,且EF=ED,EF⊥ED.
求证:AE平分∠BAD.
16.如图,在△ABC中,点O是AC边上一动点,过点O作BC的平行线交∠ACB的角平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形CEAF是矩形?请证明你的结论.
(3)在(2)问的结论下,若AE=3,EC=4,AB=12,BC=13,求△ABC的面积.
参考答案
4.C
2.A
3.C
4.C
5.B
6.B
7.A
8.A
9.答案为:2.5.
10.答案为:45°
11.答案为:67.5°,
12.答案为:∠2=∠3
13.答案为:62
14.答案为:.
15.提示:证明△BFE≌△CED,从而BE=DC=AB,∴∠BAE=45°,可得AE平分∠BAD
16.(1)证明:∵EF∥BC,
∴∠OEC=∠BCE,
∵CE平分∠ACB,
∴∠BCE=∠OCE,
∴∠OEC=∠OCE,
∴EO=CO,
同理:FO=CO,∴EO=FO;
(2)解:当点O运动到AC的中点时,四边形CEAF是矩形;
理由如下:由(1)得:EO=FO,
又∵O是AC的中点,
∴AO=CO,
∴四边形CEAF是平行四边形,
∵EO=FO=CO,
∴EO=FO=AO=CO,
∴EF=AC,
∴四边形CEAF是矩形;
(3)解:由(2)得:四边形CEAF是矩形,
∴∠AEC=90°,
∴AC===5,△ACE的面积=AE×EC=×3×4=6,
∵122+52=132,即AB2+AC2=BC2,
∴△ABC是直角三角形,∠BAC=90°,
∴△ABC的面积=AB?AC=×12×5=30.
随堂练习
一、选择题
1.如图,将矩形纸片ABCD沿对角线BD折叠一次,则图中全等三角形有(??? )
A.2对?? ?? B. 3对?? C. 4对??? D.5对
2.Rt△ABC中,∠C=90°,锐角为30°,最短边长为5cm,则最长边上的中线是( )
A.5cm B.15cm C.10cm D.2.5cm
3.如图,在矩形ABCD中,DE平分∠ADC交BC于点E,EF⊥AD交AD于点F,若EF=3,AE=5,则AD等于( )
A.5 B.6 C.7 D.8
4.如图,矩形ABCD的顶点A、C分别在直线a、b上,且a∥b,∠1=60°,则∠2的度数为( )
A.30° B.45° C.60° D.75°
5.如图,把矩形纸片ABCD纸沿对角线折叠,设重叠部分为△EBD,那么下列说法错误的是( )
A.△EBD是等腰三角形,EB=ED B.折叠后∠ABE和∠CBD一定相等
C.折叠后得到的图形是轴对称图形 D.△EBA和△EDC一定是全等三角形
6.如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )
A.△AFD≌△DCE B.AF=AD C.AB=AF D.BE=AD﹣DF
7.如图,矩形ABCD中,E在AD上,EF⊥EC,EF=EC,DE=2,矩形周长为16,则AE长是( )
A.3??? B.4?? ? C.5??? D.7
8.如图,已知矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点D与点B重合,折痕为EF,则△ABE的面积为( )
A.6cm2 B.8cm2 C.10cm2 D.12cm2
二、填空题
9.如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,则EF= cm.
10.如图,将矩形纸片ABCD折叠,使边AB、CB均落在对角线BD上,得折痕BE、BF,则∠EBF= °.
11.如图,在矩形ABCD中,AE⊥BD于E,∠DAE=3∠EAB,则∠ACD的度数为 .
12.如图是叠放在一起的两张长方形卡片,图中有∠1、∠2、∠3,则其中一定相等的是_____
13.将一张长方形纸片折叠成如图所示的形状,若∠DBC=56°,则∠1= °.
14.如图,在矩形ABCD中,AB=10,AD=6,E为BC上一点,把△CDE沿DE折叠,使点C落在AB边上的F处,则CE的长为 ?? .
三、解答题
15.如图,已知在矩形ABCD中,E、F分别是边BC、AB上的点,且EF=ED,EF⊥ED.
求证:AE平分∠BAD.
16.如图,在△ABC中,点O是AC边上一动点,过点O作BC的平行线交∠ACB的角平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形CEAF是矩形?请证明你的结论.
(3)在(2)问的结论下,若AE=3,EC=4,AB=12,BC=13,求△ABC的面积.
参考答案
4.C
2.A
3.C
4.C
5.B
6.B
7.A
8.A
9.答案为:2.5.
10.答案为:45°
11.答案为:67.5°,
12.答案为:∠2=∠3
13.答案为:62
14.答案为:.
15.提示:证明△BFE≌△CED,从而BE=DC=AB,∴∠BAE=45°,可得AE平分∠BAD
16.(1)证明:∵EF∥BC,
∴∠OEC=∠BCE,
∵CE平分∠ACB,
∴∠BCE=∠OCE,
∴∠OEC=∠OCE,
∴EO=CO,
同理:FO=CO,∴EO=FO;
(2)解:当点O运动到AC的中点时,四边形CEAF是矩形;
理由如下:由(1)得:EO=FO,
又∵O是AC的中点,
∴AO=CO,
∴四边形CEAF是平行四边形,
∵EO=FO=CO,
∴EO=FO=AO=CO,
∴EF=AC,
∴四边形CEAF是矩形;
(3)解:由(2)得:四边形CEAF是矩形,
∴∠AEC=90°,
∴AC===5,△ACE的面积=AE×EC=×3×4=6,
∵122+52=132,即AB2+AC2=BC2,
∴△ABC是直角三角形,∠BAC=90°,
∴△ABC的面积=AB?AC=×12×5=30.
